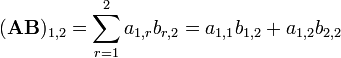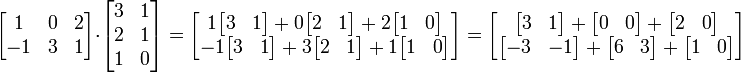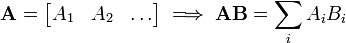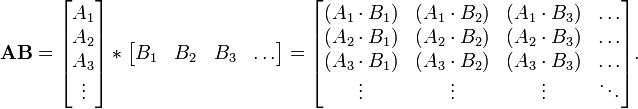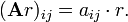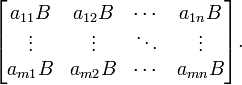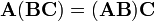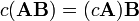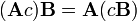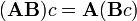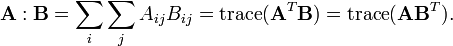Contenido Checked

La multiplicación de matrices

Temas relacionados: Matemáticas

Sabías ...

SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . Una rápida conexión para el apadrinamiento de niños es http://www.sponsor-a-child.org.uk/

En matemáticas , la multiplicación de matrices es la operación de multiplicar una matriz , ya sea con un escalar u otra matriz. Este artículo ofrece una visión general de las diversas formas de realizar la multiplicación de matrices.

Producto de matriz Ordinario

Esta es la forma más frecuente y más importante para multiplicar matrices. Se define entre dos matrices sólo si el número de columnas de la primera matriz es el mismo que el número de filas de la segunda matriz. Si A es una matriz m -by- n y B es una matriz de n -by- p, entonces su producto es una matriz m -by- p denota por AB (o, a veces A · B). Si C = AB, y c i, j indica la entrada en C en la posición (i, j), entonces

c_ {i, j} = \ sum_ {r = 1} ^ n a_ {i, r} b_ {r, j} = a_ {i, 1} b_ {1, j} + a_ {i, 2} b_ { 2, j} + \ cdots + a_ {i, n} b_ {n, j}.

para cada par i y j con 1 ≤ i ≤ m, y 1 ≤ j ≤ p. El sistema algebraica de " unidades de la matriz "resume las propiedades abstractas de este tipo de multiplicación.

Cálculo directamente de la definición

Matrix diagrama de multiplicación 2.svg

La imagen de la izquierda muestra cómo calcular el (1,2) y el elemento (3,3) elemento de AB si A es una matriz de 4 × 2, y B es una matriz 2 × 3. Los elementos de cada matriz están emparejados en la dirección de las flechas; cada par se multiplica y se añaden los productos. La ubicación del número resultante en AB corresponde a la fila y columna que se consideraron.

(\ Mathbf {AB}) _ {1,2} = \ sum_ {r = 1} ^ 2 a_ {1, r} b_ {r, 2} = a_ {1,1} b_ {1,2} + a_ {1,2} b_ {2,2}
(\ Mathbf {AB}) _ {3,3} = \ sum_ {r = 1} ^ 2 a_ {3, r} b_ {r, 3} = a_ {3,1} b_ {1,3} + a_ {3,2} b_ {2,3}

Por ejemplo:

\ Begin {bmatrix} 1 & 0 & 2 \\ -1 y 3 & 1 \ end {bmatrix} \ cdot \ begin {} bmatrix 3 & 1 \\ 2 & 1 \\ 1 & 0 \ end {bmatrix} = \ begin {bmatrix} 1 \ veces 3 + 0 \ Tiempos 2 + 2 \ épocas 1 & 1 \ Tiempos 1 + 0 \ Tiempos 1 + 2 \ Tiempos 0 \\ -1 \ veces 3 + 3 \ Tiempos 2 + 1 \ times 1 y -1 \ veces 1 + 3 \ Tiempos 1 + 1 \ Tiempos 0 \ end {bmatrix} = \ begin {bmatrix} 5 y 1 \\ 4 y 2 \ end {bmatrix}

El método de los coeficientes de los vectores

Esta multiplicación de la matriz también se puede considerar desde un punto de vista ligeramente diferente: se añade vectores juntos después de haber sido multiplicado por diferentes coeficientes. Si A y B son matrices dadas por:

\ Mathbf {A} = \ begin {bmatrix} a_ {1,1} & a_ {1,2} y \ dots \\ a_ {2,1} & a_ {2,2} y \ dots \\ \ vdots y \ vdots & \ ddots \ end {bmatrix} y \ Mathbf {B} = \ begin {} bmatrix b_ {1,1} y b_ {1,2} y \ dots \\ b_ {2,1} y b_ {2,2} y \ dots \\ \ vdots y \ vdots & \ ddots \ end {bmatrix} = \ begin {} bmatrix B_1 \\ B_2 \\ \ vdots \ end {bmatrix}

entonces

\ Mathbf {AB} = \ begin {bmatrix} a_ {1,1} B_1 + a_ {1,2} B_2 + \ cdots \\\\ a_ {2,1} B_1 + a_ {2,2} B_2 + \ cdots \\ \ vdots \ end {bmatrix}

El ejemplo revisitado:

\ Begin {bmatrix} 1 & 0 & 2 \\ -1 y 3 & 1 \ end {bmatrix} \ cdot \ begin {} bmatrix 3 & 1 \\ 2 & 1 \\ 1 & 0 \ end {bmatrix} = \ begin {bmatrix} 1 \ begin {} bmatrix 3 & 1 \ end {bmatrix} + 0 \ begin {bmatrix} 2 & 1 \ end {bmatrix} + 2 \ begin {bmatrix} 1 & 0 \ end {bmatrix} \\ -1 \ begin {} bmatrix 3 & 1 \ end {bmatrix} + 3 \ begin {bmatrix} 2 & 1 \ end {bmatrix} + 1 \ begin {bmatrix} 1 & 0 \ end {bmatrix} \ end {bmatrix} = \ begin {bmatrix} \ begin {} bmatrix 3 & 1 \ end {bmatrix} + \ begin {bmatrix} 0 & 0 \ end {bmatrix} + \ begin {bmatrix} 2 & 0 \ end {bmatrix} \\ \ begin {bmatrix} -3 y -1 \ end {bmatrix} + \ begin {bmatrix} 6 y 3 \ end {bmatrix} + \ begin {bmatrix} 1 & 0 \ end {bmatrix} \ end {bmatrix}
= \ Begin {bmatrix} 5 y 1 \\ 4 y 2 \ end {bmatrix}

Las filas de la matriz de la izquierda son la lista de coeficientes. La matriz de la derecha es la lista de los vectores. En el ejemplo, la primera fila es [1 0 2], y por lo tanto tomamos 1 veces el primer vector, 0 veces el segundo vector, y 2 veces el tercer vector.

La ecuación se puede simplificar aún más mediante el uso de productos exteriores:

\ Mathbf {A} = \ begin {} bmatrix A_1 y A_2 y \ dots \ end {bmatrix} \ implica \ mathbf {AB} = \ sum_i A_iB_i

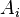Los términos de esta suma son matrices de la misma forma, cada uno que describe el efecto de una columna de A y una fila de B en el resultado. Las columnas de A pueden ser vistos como un sistema de coordenadas de la transformada, es decir, dado un vector x tenemos \ mathbf {A} x = A_1x_1 + A_2x_2 + \ cdots donde x_i son las coordenadas a lo largo de la A_i "Hachas". Los términos 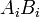A_iB_i son como 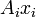A_ix_i , Excepto que 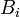B_i contiene el i-ésimo de coordenadas para cada vector columna de B, cada uno de forma independiente que se transforma en paralelo.

El ejemplo revisitado:

\ Begin {bmatrix} 1 & 0 & 2 \\ -1 y 3 & 1 \ end {bmatrix} \ cdot \ begin {} bmatrix 3 & 1 \\ 2 & 1 \\ 1 & 0 \ end {bmatrix} = \ begin {} bmatrix 1 \\ -1 \ end {bmatrix} \ begin {} bmatrix 3 & 1 \ end {bmatrix} + \ begin {bmatrix} 0 \\ 3 \ end {bmatrix} \ begin {bmatrix} 2 & 1 \ end {bmatrix} + \ begin {bmatrix} 2 \\ 1 \ end {bmatrix} \ begin {bmatrix} 1 & 0 \ end {bmatrix}
= \ Begin {bmatrix} 1 \ cdot 3 & 1 \ cdot 1 \\ -1 \ cdot 3 y -1 \ cdot 1 \ end {bmatrix} + \ begin {bmatrix} 0 \ cdot 2 & 0 \ cdot 1 \\ 3 \ cdot 2 y 3 \ cdot 1 \ end {bmatrix} + \ begin {bmatrix} 2 \ cdot 1 y 2 \ cdot 0 \\ 1 \ cdot 1 & 1 \ cdot 0 \ end {bmatrix} = \ begin {bmatrix } 5 y 1 \\ 4 y 2 \ end {bmatrix}

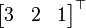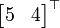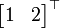Los vectores \ Begin {} bmatrix 3 & 2 & 1 \ end {bmatrix} ^ \ superior y \ Begin {bmatrix} 1 & 1 y 0 \ end {bmatrix} ^ \ superior han sido transformadas para \ Begin {} bmatrix de 5 y 4 \ end {bmatrix} ^ \ superior y \ Begin {bmatrix} 1 & 2 \ end {bmatrix} ^ \ superior en paralelo. Uno también ellos podría transformar uno por uno con los mismos pasos:

\ Begin {bmatrix} 1 & 0 & 2 \\ -1 y 3 & 1 \ end {bmatrix} \ cdot \ begin {bmatrix} \\ 3 2 1 \\ \ end {bmatrix} = \ begin {bmatrix} 1 \ \ -1 \ end {} bmatrix 3+ \ begin {bmatrix} 0 \\ 3 \ end {bmatrix} 2 + \ begin {bmatrix} 2 \\ 1 \ end {bmatrix} 1 = \ begin {bmatrix} 1 \ cdot 3 \\ -1 \ cdot 3 \ end {bmatrix} + \ begin {bmatrix} 0 \ cdot 2 \\ 3 \ cdot 2 \ end {bmatrix} + \ begin {bmatrix} 2 \ cdot 1 \\ 1 \ cdot 1 \ end {bmatrix} = \ begin {} bmatrix 5 \\ 4 \ end {bmatrix}

Método vectoriales listas

El producto de matriz común puede ser pensado como una punto producto de un lista-columnas de vectores y un fila-lista de vectores. Si A y B son matrices dadas por:

\ Mathbf {A} = \ begin {bmatrix} a_ {1,1} & a_ {1,2} y a_ {1,3} y \ dots \\ a_ {2,1} & a_ {2,2} & a_ {2,3} y \ dots \\ a_ {3,1} y a_ {3,2} & a_ {3,3} y \ dots \\ \ vdots & \ vdots & \ vdots & \ ddots \ end { bmatrix} = \ begin {} bmatrix A_1 \\ \\ A_2 A_3 \\ \ vdots \ end {bmatrix} y \ Mathbf {B} = \ begin {} bmatrix b_ {1,1} y b_ {1,2} y b_ {1,3} y \ dots \\ b_ {2,1} y b_ {2,2} & b_ {2,3} y \ dots \\ b_ {3,1} y b_ {3,2} y {3,3} b_ & \ dots \\ \ vdots & \ vdots & \ vdots & \ ddots \ end { bmatrix} = \ begin {} bmatrix B_1 y B_2 y B_3 y \ dots \ end {bmatrix}

donde

A1 es el vector fila de todos los elementos de la forma a 1, X A2 es el vector fila de todos los elementos de la forma a 2, x, etc.,
y B 1 es el vector columna de todos los elementos de la forma b x, 1 B 2 es el vector columna de todos los elementos de la forma b x, 2 etc,

entonces

\ Mathbf {AB} = \ begin {} bmatrix A_1 \\ \\ A_2 A_3 \\ \ vdots \ end {bmatrix} * \ begin {} bmatrix B_1 y B_2 y B_3 y \ dots \ end {bmatrix} = \ begin { bmatrix} (a_1 \ cdot b_1) y (a_1 \ cdot B_2) y (a_1 \ cdot B_3) y \ dots \\ (A_2 \ cdot B_1) & (A_2 \ cdot B_2) & (A_2 \ cdot B_3) y \ dots \\ (A_3 \ cdot B_1) & (A_3 \ cdot B_2) & (A_3 \ cdot B_3) y \ dots \\ \ vdots & \ vdots & \ vdots & \ ddots \ end {bmatrix}.

Propiedades

La multiplicación de matrices no es conmutativa (es decir, BA AB ≠), excepto en casos especiales. Es fácil ver por qué: no se puede esperar para cambiar las proporciones con los vectores y obtener el mismo resultado. También es fácil ver cómo el orden de los factores determina el resultado cuando se sabe que el número de columnas de la matriz de proporciones tiene que ser el mismo que el número de filas de la matriz de vectores: tienen que representar el mismo número de vectores.

Aunque la multiplicación de matrices no es conmutativa, los determinantes de AB y BA son siempre iguales (si A y B son matrices cuadradas del mismo tamaño). Ver el artículo sobre los factores determinantes de una explicación. Sin embargo la multiplicación de matrices es conmutativo cuando ambas matrices son diagonal y de la misma dimensión.

Esta noción de multiplicación es importante porque si A y B son interpretados como transformaciones lineales (que se realiza casi universalmente), entonces el producto de la matriz AB corresponde a la composición de las dos transformaciones lineales, con B se aplican primero.

Además, todas las nociones de la multiplicación de matrices descritas aquí comparten un conjunto de propiedades comunes se describen a continuación.

Algoritmos

La complejidad de la multiplicación de matrices, de llevarse a cabo, ingenuamente, es O (n ³), pero existen algoritmos más eficientes. El algoritmo de Strassen, ideado por Volker Strassen en 1969 y, a menudo se refiere como "la multiplicación de matrices rápido", se basa en una forma inteligente de multiplicar dos 2 × 2 matrices que requiere sólo 7 multiplicaciones (en lugar de la habitual 8). La aplicación de este truco recursiva da un algoritmo con un coste de 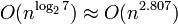O (n ^ {\ log_ {2} 7}) \ aprox O (n ^ {2,807}) . En la práctica, sin embargo, rara vez se utiliza, ya que es difícil de implementar y que carece estabilidad numérica. El factor constante implícita en el notación O grande es aproximadamente 4.695.

La algoritmo con el exponente más bajo conocido, que fue presentado por Don Calderero y Shmuel Winograd en 1990 , tiene una complejidad asintótica de O (n 2.376). Es similar al algoritmo de Strassen: una forma inteligente se ideó para multiplicar dos matrices k × k con un menor número de multiplicaciones ³ k, y esta técnica se aplica de forma recursiva. Mejora en el factor constante en el algoritmo de Strassen, reduciéndolo a 4.537. Sin embargo, el término constante implícita en la O (n 2.376) resultado es tan grande que el algoritmo de Calderero-Winograd es sólo vale la pena para las matrices que son demasiado grandes para manejar en las computadoras de hoy en día (Knuth, 1998).

Desde cualquier algoritmo para multiplicar dos matrices n × n tiene que procesar todo 2 × n ² entradas, hay un asintótica límite inferior de Ω (n ²) operaciones. Raz (2002) demuestra un límite inferior de \ Omega (m ^ 2 \ log m) para circuitos coeficiente aritméticas acotados sobre los números reales o complejos.

Cohn et al. (2003, 2005) puso de métodos tales como los algoritmos de Strassen y Calderero-Winograd en una totalmente diferente, grupo teórico contexto. Ellos muestran que si las familias de , existen productos guirnalda de abeliano con grupos simétricos que satisfacen ciertas condiciones existe algoritmos de la multiplicación de matrices con complejidad cuadrática esencial. La mayoría de los investigadores creen que este es el caso (Robinson, 2005).

Multiplicación escalar

La multiplicación escalar de una matriz A = (a ij) y un escalar r da un producto r A del mismo tamaño que A. Las entradas de r A se dan por

(R \ mathbf {A}) _ {ij} = r \ cdot a_ {ij}. \,

Por ejemplo, si

\ Mathbf {A} = \ begin {bmatrix} 1 & 2 \\ 3 y 4 \ end {bmatrix}

entonces

7 \ mathbf {A} = \ begin {bmatrix} 7 \ cdot 1 y 7 \ cdot 2 \\ 7 \ cdot 3 y 7 \ cdot 4 \ end {bmatrix} = \ begin {bmatrix} 7 y 14 \\ 21 & 28 \ end {bmatrix}.

Si estamos interesados en matrices más de un anillo, entonces la multiplicación anterior a veces se llama la multiplicación izquierda, mientras que la multiplicación derecho se define como

(\ Mathbf {A} r) _ {ij} = a_ {ij} \ cdot r. \,

Cuando el anillo subyacente es conmutativa , por ejemplo, el campo de número real o complejo, las dos multiplicaciones son los mismos. Sin embargo, si el anillo no es conmutativa, tal como el cuaterniones, que pueden ser diferentes. Por ejemplo

i \ begin {bmatrix} i y 0 \\ 0 & j \\ \ end {bmatrix} = \ begin {bmatrix} -1 y 0 \\ 0 & k \\ \ end {bmatrix} \ ne \ begin {bmatrix} -1 y 0 \\ 0 & -k \\ \ end {bmatrix} = \ begin {bmatrix} i y 0 \\ 0 & j \\ \ end {bmatrix} i.

Producto de Hadamard

Durante dos matrices de las mismas dimensiones, tenemos el producto Hadamard, también conocido como el producto entrywise y el producto Schur. Se puede generalizar para mantener no sólo para matrices, sino también para los operadores. La Hadamard producto de dos m -by- n matrices A y B, denotado por A • B, es un m -by- n matriz dada por (A • B) ij = a ij b ij. Por ejemplo

\ Begin {bmatrix} 1 & 2 \\ 3 & 1 \\ \ end {bmatrix} \ bullet \ begin {bmatrix} 0 & 3 \\ 2 & 1 \\ \ end {bmatrix} = \ begin {bmatrix} 1 \ cdot 0 y 2 \ cdot 3 \\ 3 \ cdot 2 & 1 \ cdot 1 \\ \ end {bmatrix} = \ begin {bmatrix} 0 & 6 \\ 6 & 1 \\ \ end {bmatrix} .

Tenga en cuenta que el producto Hadamard es una submatriz del producto de Kronecker (ver abajo).

El producto Hadamard es conmutativa .

El producto de Hadamard es estudiado por los teóricos de la matriz, y se presenta en algoritmos de compresión con pérdidas, tales como JPEG, pero es prácticamente intacta por algebristas lineales. Se discute en (Horn & Johnson, 1994, Ch. 5).

Producto Kronecker

Para cualquier dos matrices arbitrarias A y B, tenemos el producto directo o Producto Kronecker A ⊗ B se define como

\ Begin {bmatrix} a_ {11} B & a_ {12} B & \ cdots y a_ {1n} B \\ \ vdots & \ vdots & \ ddots & \ vdots \\ a_ {m1} B & a_ {m2} B & \ cdots y a_ {mn} B \ end {bmatrix}.

Tenga en cuenta que si A es m -by- n y B es p -by- r entonces A ⊗ B es un mp -by- nr matriz. Una vez más esta multiplicación no es conmutativa.

Por ejemplo

\ Begin {bmatrix} 1 & 2 \\ 3 & 1 \\ \ end {bmatrix} \ otimes \ begin {bmatrix} 0 & 3 \\ 2 & 1 \\ \ end {bmatrix} = \ begin {bmatrix} 1 \ cdot 0 & 1 \ cdot 3 & 2 \ cdot 0 y 2 \ cdot 3 \\ 1 \ cdot 2 & 1 \ cdot 1 y 2 \ cdot 2 & 2 \ cdot 1 \\ 3 \ cdot 0 y 3 \ cdot 3 & 1 \ cdot 0 & 1 \ cdot 3 \\ 3 \ cdot 2 y 3 \ cdot 1 & 1 \ cdot 2 & 1 \ cdot 1 \\ \ end {bmatrix} = \ begin {bmatrix} 0 & 3 & 0 & 6 \\ 2 y 1 y 4 y 2 \\ 0 & 9 y 0 y 3 \\ 6 & 3 & 2 & 1 \ end {bmatrix} .

Si A y B representan las transformaciones lineales V 1 → W 1 y V 2 → W 2, respectivamente, entonces A ⊗ B representa el producto tensorial de los dos mapas, V 1 ⊗ V 2 → W 1 ⊗ W 2.

Las propiedades comunes

El wikilibro El libro de matemáticas pruebas tiene una página sobre el tema de: Las pruebas de propiedades de las matrices

Los tres conceptos de la multiplicación de matrices son asociativa :

\ \ Mathbf {A} (\ mathbf {AC}) = (\ mathbf {AB}) \ mathbf {C}

y distributiva:

\ \ Mathbf {A} (\ mathbf {B} + \ mathbf {C}) = \ mathbf {AB} + \ mathbf {AC}

y

\ (\ Mathbf {A} + \ vec {B}) \ mathbf {C} = \ mathbf {AC} + \ mathbf {BC} .

y compatible con la multiplicación escalar:

\ C (\ mathbf {AB}) = (c \ mathbf {A}) \ mathbf {B}
\ (\ Mathbf {A} c) \ mathbf {B} = \ mathbf {A} (c \ mathbf {B})
\ (\ Mathbf {AB}) c = \ mathbf {A} (\ mathbf {B} c)

Tenga en cuenta que estos tres parejas separadas de las expresiones serán iguales entre sí sólo si la multiplicación y la suma en el campo escalar son conmutativas, es decir, el campo escalar es un anillo conmutativo. Ver multiplicación escalar por encima de un contra-ejemplo como el campo escalar de cuaterniones.

Producto interno Frobenius

El producto interno Frobenius, a veces denota A: B es el producto interno-componente racional de dos matrices como si son vectores. En otras palabras, es la suma de las entradas del producto Hadamard, es decir,

\ Mathbf {A}: \ mathbf {B} = \ sum_i \ sum_j A_ {ij} B_ {ij} = \ operatorname {trace} (\ mathbf {A} ^ T \ mathbf {B}) = \ operatorname {trace} (\ mathbf {A} \ mathbf {B} ^ T).

Este producto interior induce la Norma de Frobenius.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Matrix_multiplication&oldid=203157436 "