Equilibrio de Nash
Antecedentes
SOS Children han producido una selección de artículos de la Wikipedia para escuelas desde 2005. Apadrina un niño para hacer una diferencia real.
| Equilibrio de Nash | |
|---|---|
| La concepto de la solución en la teoría de juegos | |
| Relaciones | |
| Subconjunto de | Rationalizability, Epsilon-equilibrio, Equilibrio correlacionado |
| Superconjunto de | Evolutivamente estrategia estable , Equilibrio perfecto en subjuegos, Equilibrio bayesiano perfecto, Equilibrio perfecto de mano temblorosa |
| Significado | |
| Propuesto por | John Forbes Nash |
| Utilizado para | Todos los juegos no cooperativos |
| Ejemplo | Dilema del prisionero |
En la teoría de juegos , el equilibrio de Nash (nombrado después John Forbes Nash, que la propuso) es un concepto de la solución de un juego entre dos o más jugadores, en el que ningún jugador tiene nada que ganar cambiando sólo su propia estrategia unilateral. Si cada jugador ha optado por una estrategia y ningún jugador puede beneficiarse cambiando su estrategia mientras los otros jugadores conservan la suya sin cambios, entonces el conjunto actual de opciones de estrategia y los pagos correspondientes constituyen un equilibrio de Nash.
En pocas palabras, Amy y Bill están en el equilibrio de Nash si Amy está haciendo la mejor decisión que puede, teniendo en cuenta la decisión de Bill, y Bill está haciendo la mejor decisión que puede, teniendo en cuenta la decisión de Amy. Del mismo modo, muchos jugadores están en el equilibrio de Nash si cada uno está haciendo la mejor decisión que puede, teniendo en cuenta las decisiones de los demás. Sin embargo, el equilibrio de Nash no significa necesariamente la mejor rentabilidad acumulada de todos los actores involucrados; en muchos casos todos los jugadores pueden mejorar sus beneficios si de alguna manera podrían acordar estrategias diferentes del equilibrio de Nash (ej. los empresarios que compiten formando una cartel con el fin de aumentar sus beneficios).
Historia
El concepto de equilibrio de Nash (NE) no es completamente original para Nash (por ejemplo, Antoine Augustin Cournot mostró cómo encontrar lo que ahora llamamos el equilibrio de Nash del Cournot juego duopolio). En consecuencia, algunos autores se refieren a él como un "equilibrio de Cournot-Nash" (o como un "equilibrio de Nash-Cournot"). Sin embargo, Nash demostró por primera vez en su disertación, los juegos no cooperativos (1950), que el equilibrio de Nash (en estrategias mixtas) debe existir para todos los juegos finitos con cualquier número de jugadores. Antes del trabajo de Nash, esto sólo se había demostrado para dos jugadores juegos de suma cero (por John von Neumann y Oskar Morgenstern en 1947).
Definiciones
Definición informal
Informalmente, un conjunto de estrategias es un equilibrio de Nash si ningún jugador puede hacer mejor al cambiar unilateralmente su estrategia. Como heurístico, uno puede imaginar que a cada jugador se le dijo a las estrategias de los otros jugadores. Si cualquier jugador querría hacer algo diferente después de ser informado acerca de las estrategias de los demás, entonces ese conjunto de estrategias no es un equilibrio de Nash. Sin embargo, si el jugador no quiere cambiar (o es indiferente entre la conexión y no), entonces el conjunto de estrategias es un equilibrio de Nash.
Esto puede tener consecuencias contrarias a la intuición. Dado que el equilibrio de Nash se centra en las preferencias de un individuo, dado que los otros mantienen sus opciones fijas, no puede haber equilibrios de Nash en el que, si los jugadores podrían coordinar, todos se quieren cambiar. La caza del ciervo presenta un ejemplo de este fenómeno.
Definición formal
Sea (S, f) ser un juego, donde S es el conjunto de perfiles de estrategia y f es el conjunto de perfiles de recompensa. Dejar 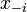 ser un perfil de estrategia de todos los jugadores, excepto para el jugador
ser un perfil de estrategia de todos los jugadores, excepto para el jugador  . Cuando cada jugador
. Cuando cada jugador  elige estrategia
elige estrategia  resultante en el perfil de estrategia
resultante en el perfil de estrategia  entonces el jugador
entonces el jugador  obtiene recompensa
obtiene recompensa  . Tenga en cuenta que la rentabilidad depende del perfil de la estrategia elegida, es decir, de la estrategia elegida por el jugador
. Tenga en cuenta que la rentabilidad depende del perfil de la estrategia elegida, es decir, de la estrategia elegida por el jugador  así como las estrategias elegidas por todos los otros jugadores. Un perfil de estrategia
así como las estrategias elegidas por todos los otros jugadores. Un perfil de estrategia 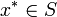 es un equilibrio de Nash (NE) si no hay desviación unilateral de estrategia por parte de cualquier jugador es rentable, que se
es un equilibrio de Nash (NE) si no hay desviación unilateral de estrategia por parte de cualquier jugador es rentable, que se
Un juego puede tener una NE estrategia pura o un NE en su extensión mixta (el de la elección de una estrategia pura estocásticamente con un fijo frecuencia). Nash demostró que, si permitimos estrategias mixtas (jugadores eligen estrategias al azar de acuerdo a las probabilidades pre-asignados), entonces cada n-jugador del juego en el que cada jugador puede elegir entre un número finito de estrategias admite al menos un equilibrio de Nash.
Ejemplos
Juego de la Competencia
| El jugador 2 elige '0' | El jugador 2 elige '1' | '2' del jugador 2 elige | El jugador 2 elige '3' | |
|---|---|---|---|---|
| Jugador 1 elige '0' | 0, 0 | 2, -2 | 2, -2 | 2, -2 |
| Jugador 1 elige '1' | -2, 2 | 1, 1 | 3, -1 | 3, -1 |
| '2' El jugador 1 elige | -2, 2 | -1, 3 | 2, 2 | 4, 0 |
| Jugador 1 elige '3' | -2, 2 | -1, 3 | 0, 4 | 3, 3 |
Esto puede ser ilustrado por un juego de dos jugadores en el que ambos jugadores eligen simultáneamente un número entero de 0 a 3 y ambos ganan el menor de los dos números en puntos. Además, si un jugador elige un número mayor que el otro, entonces él / ella tiene que renunciar a dos puntos a la otra. Este juego tiene un único equilibrio de Nash: ambos jugadores eligen 0 (resaltado en rojo claro). Cualquier otra opción de estrategias se puede mejorar si uno de los jugadores disminuye su número a uno menos que el número del otro jugador. En la tabla a la izquierda, por ejemplo, cuando empezaba en el cuadrado verde está en el interés del jugador 1 para pasar a la plaza púrpura eligiendo un número más pequeño, y está en el interés del jugador 2 para pasar al cuadrado azul por la elección de un número más pequeño. Si el juego se modifica para que los dos jugadores ganan la cantidad nombre si ambos eligen el mismo número, y por lo demás ganan nada, entonces hay 4 equilibrios de Nash (0,0 ... 1,1 ... 2,2. ..y 3,3).
Juego de Coordinación
| Jugador 2 adopta la estrategia 1 | Jugador 2 adopta la estrategia 2 | |
|---|---|---|
| Jugador 1 adopta la estrategia 1 | A, A | B, C |
| Jugador 1 adopta la estrategia 2 | C, B | D, D |
El juego de coordinación es un clásico ( simétrica) de dos jugadores, dos juego de estrategia, con la matriz de pagos se muestra a la derecha, donde los pagos satisfacen A> C y D> B. Así, los jugadores deben coordinar, ya sea en una o en D, para recibir una alta rentabilidad. Si las opciones de los jugadores no coinciden, un pago inferior es recompensado. Un ejemplo de un juego de coordinación es el escenario en el que dos tecnologías están disponibles para dos empresas con productos compatibles, y tienen que elegir una estrategia para convertirse en el estándar del mercado. Si ambas empresas coinciden en la tecnología elegida, se espera que las altas ventas de ambas empresas. Si las firmas no coinciden en la tecnología estándar, resultado pocas ventas. Ambas estrategias son equilibrios de Nash del juego.
Conducción en una carretera, y tener que elegir entre conducir por la izquierda o para conducir a la derecha de la carretera, es también un juego de coordinación. Por ejemplo, con ganancias de 100 significa que no hay choque y 0 significa un choque, el juego de coordinación se puede definir con la siguiente matriz de pagos:
| Conduzca por la izquierda | Conducir por la derecha | |
|---|---|---|
| Conduzca por la izquierda | 100, 100 | 0, 0 |
| Conducir por la derecha | 0, 0 | 100, 100 |
En este caso hay dos equilibrios de Nash en estrategias puras, cuando tanto elegir a cualquiera de conducir por la izquierda o por la derecha. Si admitimos estrategias mixtas (cuando se elige una estrategia pura al azar, sujeto a alguna probabilidad fija), a continuación, hay tres equilibrios de Nash para el mismo caso: dos que hemos visto desde la forma en estrategias puras, donde las probabilidades son (0%, 100 %) para el jugador uno, (0%, 100%) para dos jugadores; y (100%, 0%) para el jugador uno, (100%, 0%) para el jugador dos, respectivamente. Añadimos otra donde las probabilidades de cada jugador es (50%, 50%).
Dilema del prisionero
(Pero cuidado con las diferencias en la orientación de la matriz de pagos)
El dilema del prisionero tiene la misma matriz de pagos como se muestra para el juego de coordinación, pero ahora C> A> D> B. Debido C> A y D> B, cada jugador mejora su situación por el cambio de la estrategia # 1 a la estrategia # 2, no importa lo que decida el otro jugador. Por tanto, El dilema del prisionero tiene un único equilibrio de Nash: ambos jugadores eligen la estrategia # 2 ("traicionar"). Lo que ha hecho siempre este un caso interesante para estudiar es el hecho de que D <A ("ambos traicionan") es globalmente inferior a "ambos siguen siendo leales". La estrategia óptima a nivel mundial es inestable; no es un equilibrio.
Como Ian Stewart dijo, "a veces las decisiones racionales no son sensibles!".
Equilibrios de Nash en una matriz de pagos
Hay una forma numérica fácil de identificar equilibrio de Nash en una matriz de pago. Es especialmente útil en dos Juegos para una persona donde los jugadores tienen más de dos estrategias. En este caso el análisis formal puede llegar a ser demasiado largo. Esta regla no se aplica al caso en que las estrategias (estocásticos) mixtos son de interés. La regla es la siguiente: si el primer número de pagos, en el doblete de la célula, es el máximo de la columna de la celda y si el segundo número es el máximo de la fila de la celda - entonces la célula representa un equilibrio de Nash .
Podemos aplicar esta regla a una matriz de 3x3:
| Opción A | Opción B | Opción C | |
|---|---|---|---|
| Opción A | 0, 0 | 25, 40 | 5, 10 |
| Opción B | 40, 25 | 0, 0 | 5, 15 |
| Opción C | 10, 5 | 15, 5 | 10, 10 |
Usando la regla, podemos muy rápidamente (mucho más rápido que con el análisis formal) ver que las células Nash Equlibria son (B, A), (A B), y (C, C). De hecho, para la célula (B, A) 40 es el máximo de la primera columna y 25 es el máximo de la segunda fila. Para (A, B) 25 es el máximo de la segunda columna y 40 es el máximo de la primera fila. Lo mismo para celular (C, C). Para otras células, ya sea uno o ambos de los miembros Duplet no son el máximo de las filas y columnas correspondientes.
Dicho esto, la mecánica real de encontrar células de equilibrio es evidente: encontrar el máximo de una columna y compruebe si el segundo miembro de la pareja es el máximo de la fila. Si se cumplen estas condiciones, la célula representa un equilibrio de Nash. Revise todas las columnas de esta manera para encontrar todas las células NE. Una matriz de NxN puede tener entre 0 y NxN estrategia pura equilibrios de Nash.
Estabilidad
El concepto de estabilidad, útil en el análisis de muchos tipos de de equilibrio, también se puede aplicar a equilibrios de Nash.
Un equilibrio de Nash de un juego de estrategia mixta es estable si un pequeño cambio (en concreto, un cambio infinitesimal) de probabilidades para un jugador lleva a una situación en la que se cumplen dos condiciones:
- el jugador que no cambió no tiene mejor estrategia en la nueva circunstancia
- el jugador que hizo el cambio ahora está jugando con una estrategia estrictamente peor
Si tanto se cumplen estos casos, a continuación, un jugador con el pequeño cambio en su estrategia mixta volverá inmediatamente al equilibrio de Nash. El equilibrio se dice que es estable. Si la condición no se cumple uno entonces el equilibrio es inestable. Si sólo uno de ellos tenga la condición entonces no es probable que haya un número infinito de estrategias óptimas para el jugador que cambió. John Nash demostró que esta última situación no podría producirse en una gama de juegos bien definidos.
En el ejemplo de "juego de conducción" por encima hay dos equilibrios estables e inestables. Los equilibrios que involucran estrategias mixtas con 100% de probabilidades son estables. Si alguno de los jugadores cambia sus probabilidades ligeramente, van a ser a la vez en desventaja, y su oponente no tendrán ninguna razón para cambiar de estrategia por turnos. El (50%, 50%) de equilibrio es inestable. Si cualquiera de los jugadores cambia sus probabilidades, entonces el otro jugador inmediatamente tiene una mejor estrategia en cualquiera de (0%, 100%) o (100%, 0%).
La estabilidad es crucial en aplicaciones prácticas de equilibrios de Nash, ya que la estrategia mixta de cada jugador no es perfectamente conocida, pero tiene que ser deducido de la distribución estadística de sus acciones en el juego. En este caso son muy improbable que se produzca en la práctica equilibrios inestables, ya que cualquier cambio minuto en las proporciones de cada estrategia visto dará lugar a un cambio en la estrategia y la ruptura del equilibrio.
Tenga en cuenta que la estabilidad del equilibrio está relacionada con, pero es distinta de la estabilidad de una estrategia.
Un equilibrio de Nash-Coalición Proof (CPNE) (similar a un fuerte equilibrio de Nash) se produce cuando los jugadores no pueden hacer mejor, incluso si se les permite comunicarse y colaborar antes del partido. Cada estrategia se correlacionó con el apoyo de dominancia estricta reiterado y en la Frontera de Pareto es una CPNE. Además, es posible que un juego tenga un equilibrio de Nash que es resistente contra coaliciones menos de un tamaño especificado, k. CPNE está relacionada con la la teoría del núcleo.
Aparición
Si un juego tiene un único equilibrio de Nash y se juega entre los jugadores en ciertas condiciones, a continuación, se adoptarán el conjunto de estrategias NE. Condiciones suficientes para garantizar que se juega el equilibrio de Nash son:
- Los jugadores de todos harán todo lo posible para maximizar su ganancia esperada según lo descrito por el juego.
- Los jugadores son impecables en la ejecución.
- Los jugadores tienen la inteligencia suficiente para deducir la solución.
- No es de conocimiento común que todos los jugadores se reúnen estas condiciones, incluido éste. Así, no sólo se debe a cada jugador conocer a los otros jugadores se reúnen las condiciones, pero también debe saber que todos ellos saben que ellos se encuentran, y saber que ellos saben que saben que ellos se encuentran, y así sucesivamente.
Cuando no se cumplan las condiciones
Ejemplos de problemas de la teoría de juegos en los que no se cumplen estas condiciones:
- La primera condición no se cumple si el juego no describe correctamente las cantidades que un jugador desea maximizar. En este caso no hay ninguna razón particular para que el jugador a adoptar una estrategia de equilibrio. Por ejemplo, el dilema del prisionero no es un dilema si algún jugador está feliz de ser encarcelado indefinidamente.
- Imperfección intencional o accidental en la ejecución. Por ejemplo, un ordenador capaz de juego lógica impecable frente a un segundo ordenador impecable resultará en equilibrio. Introducción de la imperfección conducirá a su interrupción, ya sea a través de la pérdida para el jugador que comete el error, o por medio de la negación del cuarto criterio de "conocimiento común" lleva a una posible victoria para el jugador. (Un ejemplo podría ser un jugador que pone de repente el coche en marcha atrás en el juego de 'pollo', asegurando un escenario que no puede ganar sin pérdidas). Un ejemplo notable de esta situación en la ficción es la serie de Doctor Who Destino de los Daleks
- En muchos casos, la tercera condición no se cumple porque, a pesar de que debe existir el equilibrio, es desconocido debido a la complejidad del juego, por ejemplo, en Ajedrez chino. O, si lo sabe, puede que no sea conocida de todos los jugadores, ya que cuando se juega tic-tac-dedo del pie con un pequeño niño que desesperadamente quiere ganar (que cumple con los otros criterios).
- El cuarto criterio de conocimiento común no podría cumplirse incluso si todos los jugadores, de hecho, cumplen con todos los demás criterios. Jugadores erróneamente desconfiando racionalidad de cada uno puede adoptar contra-estrategias para esperada irracional juego en nombre de sus oponentes. Esta es una importante consideración en " Chicken "o una carrera armamentista, por ejemplo.
Cuando se cumplan las condiciones
Debido a las condiciones limitadas en las que realmente se puede observar NE, rara vez se tratan como una guía para la conducta del día a día, o se observen en la práctica en las negociaciones humanos. Sin embargo, como un concepto teórico en la economía y la biología evolutiva del NE tiene poder explicativo. La recompensa en economía es el dinero, y en la evolución de transmisión de genes biología, ambos son la línea de fondo fundamental de supervivencia. Los investigadores que aplican la teoría de juegos en estos campos afirman que los agentes no poder maximizar estos por cualquier razón se compitieron fuera del mercado o el medio ambiente, que se atribuye la capacidad de probar todas las estrategias. Esta conclusión se extrae de la " estabilidad "teoría anterior. En estas situaciones el supuesto de que la estrategia se observa es en realidad un NE a menudo ha sido confirmado por la investigación.
Prueba de la existencia
Como el anterior, y mucho  ser un perfil de estrategia mixta de todos los jugadores, excepto para el jugador
ser un perfil de estrategia mixta de todos los jugadores, excepto para el jugador  . Podemos definir una mejor respuesta correspondencia para el jugador
. Podemos definir una mejor respuesta correspondencia para el jugador  ,
,  .
.  es una relación entre el conjunto de todas las distribuciones de probabilidad más perfiles de los jugadores oponente a un conjunto de jugador
es una relación entre el conjunto de todas las distribuciones de probabilidad más perfiles de los jugadores oponente a un conjunto de jugador  's estrategias, de tal manera que cada elemento de
's estrategias, de tal manera que cada elemento de
es una mejor respuesta a  . Definir
. Definir
 .
.
Uno puede utilizar el Kakutani fija punto teorema para demostrar que  tiene un punto fijo. Es decir, hay una
tiene un punto fijo. Es decir, hay una  de tal manera que
de tal manera que 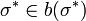 . Desde
. Desde 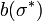 representa la mejor respuesta para todos los jugadores a
representa la mejor respuesta para todos los jugadores a  , La existencia del punto fijo demuestra que hay algún conjunto estrategia que es una mejor respuesta a sí mismo. Ningún jugador podía hacer nada mejor por desviarse, y por lo tanto es un equilibrio de Nash.
, La existencia del punto fijo demuestra que hay algún conjunto estrategia que es una mejor respuesta a sí mismo. Ningún jugador podía hacer nada mejor por desviarse, y por lo tanto es un equilibrio de Nash.
Cuando Nash hizo este punto a John von Neumann en 1949, von Neumann famoso despidió con las palabras: "Eso es trivial, ya sabes. Eso es sólo un teorema del punto fijo." (Ver Nasar, 1998, p. 94.)