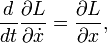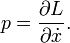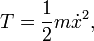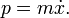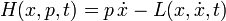Cálculo de variaciones
Antecedentes
SOS Children, que corre cerca de 200 sos escuelas en el mundo en desarrollo, organizó esta selección. patrocinio SOS Niño es cool!
Cálculo de variaciones es un campo de las matemáticas que se ocupa de extremizing funcionales, a diferencia de ordinario cálculo que se ocupa de funciones . Un funcional es generalmente una asignación de un conjunto de funciones a los números reales. Functionals se forman a menudo como integrales definidas que implican funciones desconocidas y sus derivados. El interés se centra en las funciones extremales que hacen que el funcional alcanzar un valor máximo o mínimo - o funciones fijas - aquellos en los que la tasa de variación del funcional es exactamente cero.
Quizás el ejemplo más simple de tal problema es encontrar la curva de longitud más corta, o geodésicas, que conecta dos puntos. Si no hay limitaciones, la solución es obviamente una línea recta entre los puntos. Sin embargo, si la curva está limitado a tumbarse en una superficie en el espacio, entonces la solución es menos obvio, y posiblemente puede existir muchas soluciones. Tales soluciones se conocen como geodésicas. Un problema relacionado es el que plantea El principio de Fermat: luz sigue el camino de la longitud óptica más corta que conecta dos puntos, en los que la longitud óptica depende del material del medio. Un concepto correspondiente en mecánica es la principio de mínima acción.
Muchos de los problemas importantes implican funciones de varias variables. Soluciones de problemas de contorno para el Ecuación de Laplace satisface la Principio de Dirichlet. El problema de la meseta requiere encontrar una superficie de área mínima que se extiende por un contorno dado en el espacio: la solución o soluciones pueden encontrarse a menudo por inmersión de un marco de alambre en una solución de espuma de jabón. Aunque tales experimentos son relativamente fáciles de realizar, su interpretación matemática está lejos de ser simple: puede haber más de un local minimizando la superficie, y que pueden tener topología no trivial.
Historia
El cálculo de variaciones puede decirse que comienzan con un problema de Johann Bernoulli (1696). Inmediatamente se ocupó la atención de Jakob Bernoulli y la Marqués de l'Hôpital, pero Euler primera elaboraron el tema. Sus contribuciones se iniciaron en 1733, y su Elementa Calculi Variationum dieron a la ciencia su nombre. Lagrange contribuyó ampliamente a la teoría, y Legendre (1786), ha establecido un método, no es del todo satisfactoria, para la discriminación de los máximos y mínimos. Newton y Leibniz también dieron un poco de atención temprana a la materia. Para esta discriminación Brunacci (1810), Gauss (1829), Poisson (1831), Ostrogradsky (1834), y Jacobi (1837) han sido uno de los contribuyentes. Un general de trabajo importante es el de Sarrus (1842) que se condensó y mejorado por Cauchy (1844). Otros tratados valiosos y memorias se han escrito por Strauch (1849), Jellett (1850), Hesse (1857), Clebsch (1858), y Carll (1885), pero tal vez la obra más importante del siglo es el de Weierstrass. Su curso celebrado en la teoría es que hacen época, y se puede afirmar que él fue el primero en colocar sobre una base firme e incuestionable. La 20a y la 23a Problemas de Hilbert publicados en 1900 atrajeron un mayor desarrollo. En el siglo 20 Hilbert , Noether, Tonelli, Lebesgue y Hadamard entre otros hicieron contribuciones significativas. Marston Morse cálculo de variaciones aplica en lo que ahora se llama La teoría de Morse. Pontryagin, Rockafellar y Clarke desarrolló nuevas herramientas matemáticas para teoría del control óptimo, una generalización del cálculo de variaciones.
Extrema débil y fuerte
La norma del supremo (también llamada norma infinito) para, funciones reales y continuas acotadas en un espacio topológico  se define como
se define como
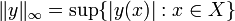 .
.
Un funcional 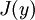 definida en un espacio apropiado de funciones
definida en un espacio apropiado de funciones  con norma
con norma 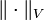 se dice que tiene un mínimo débil en la función de
se dice que tiene un mínimo débil en la función de 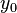 si existe alguna
si existe alguna  de tal manera que, para todas las funciones Y con
de tal manera que, para todas las funciones Y con  ,
,
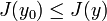 .
.
Maxima débiles se definen de manera similar, con la desigualdad en la última ecuación inversa. En la mayoría de los problemas,  es el espacio de las funciones continuamente diferenciables r -los tiempos en un subconjunto compacto
es el espacio de las funciones continuamente diferenciables r -los tiempos en un subconjunto compacto 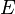 de la recta real, con su norma dada por
de la recta real, con su norma dada por
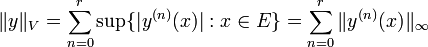 .
.
Esta norma es sólo la suma de las normas supremo de  y sus derivados.
y sus derivados.
Un funcional 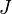 se dice que tiene un mínimo fuerte a
se dice que tiene un mínimo fuerte a 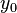 si existe alguna
si existe alguna  de tal manera que, para todas las funciones Y con
de tal manera que, para todas las funciones Y con 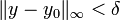 ,
, 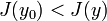 . Strong máximo se define de forma similar, pero con la desigualdad en la última ecuación invierte.
. Strong máximo se define de forma similar, pero con la desigualdad en la última ecuación invierte.
La diferencia entre los extremos fuerte y débil es que, por una fuerte extremo, 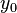 es un extremo local en relación con el conjunto de
es un extremo local en relación con el conjunto de  -Cierre funciones con respecto a la norma del supremo. En general, este (supremum) norma es diferente de la norma
-Cierre funciones con respecto a la norma del supremo. En general, este (supremum) norma es diferente de la norma 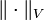 que V ha sido dotado con. Si
que V ha sido dotado con. Si 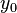 es un fuerte para extremum
es un fuerte para extremum 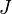 entonces también es un valor extremo débil, pero lo contrario no podrá ser titular. Encontrar fuerte extrema es más difícil que encontrar extremos débiles y en lo que sigue, se supondrá que estamos buscando extrema debilidad.
entonces también es un valor extremo débil, pero lo contrario no podrá ser titular. Encontrar fuerte extrema es más difícil que encontrar extremos débiles y en lo que sigue, se supondrá que estamos buscando extrema debilidad.
La ecuación de Euler-Lagrange
En condiciones ideales, los máximos y mínimos de una función dada pueden estar localizados mediante la búsqueda de los puntos donde su derivado se desvanece. Por analogía, las soluciones de los problemas variacionales lisas se pueden obtener mediante la resolución de la asociada Ecuación de Euler-Lagrange.
Considere lo funcional:
La función  debe tener al menos un derivado con el fin de satisfacer los requisitos para la solicitud válida de la función; Además, si el funcional
debe tener al menos un derivado con el fin de satisfacer los requisitos para la solicitud válida de la función; Además, si el funcional ![A [f]](../../images/761/76192.png) alcanza su mínimo local en
alcanza su mínimo local en 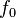 y
y  es una función arbitraria que tiene al menos un derivado y desaparece en los puntos finales
es una función arbitraria que tiene al menos un derivado y desaparece en los puntos finales 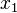 y
y 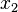 , Entonces debemos tener
, Entonces debemos tener
para cualquier número ε cerca de 0. Por lo tanto, el derivado de ![A [F_0 + \ epsilon \ eta]](../../images/761/76197.png) con respecto a ε (la primera variación de A) debe desaparecer en ε = 0.
con respecto a ε (la primera variación de A) debe desaparecer en ε = 0.
donde hemos utilizado la regla de la cadena en la segunda línea y integración por partes en el tercero. El último término de la tercera línea se desvanece porque  en los puntos extremos. Finalmente, de acuerdo con la lema fundamental del cálculo de variaciones, nos encontramos con que
en los puntos extremos. Finalmente, de acuerdo con la lema fundamental del cálculo de variaciones, nos encontramos con que  satisfaga la ecuación de Euler-Lagrange
satisfaga la ecuación de Euler-Lagrange
En general, esto da un segundo orden ecuación diferencial ordinaria que puede ser resuelto a obtener el extremal  . La ecuación de Euler-Lagrange es un necesaria, pero no suficiente, para un extremal. Condiciones suficientes para un extremal se discuten en las referencias.
. La ecuación de Euler-Lagrange es un necesaria, pero no suficiente, para un extremal. Condiciones suficientes para un extremal se discuten en las referencias.
Para ilustrar este proceso, considerar el problema de encontrar la curva más corta en el plano que conecta dos puntos  y
y  . La longitud de arco está dada por
. La longitud de arco está dada por
con
y donde 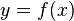 ,
, 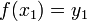 Y
Y  .
.
para cualquier elección de la función de  . Podemos interpretar esta condición como la desaparición de todo derivadas direccionales de
. Podemos interpretar esta condición como la desaparición de todo derivadas direccionales de ![A [F_0]](../../images/762/76209.png) en el espacio de las funciones diferenciables, y esto se formaliza al exigir la Derivado de Fréchet
en el espacio de las funciones diferenciables, y esto se formaliza al exigir la Derivado de Fréchet  a desaparecer en
a desaparecer en  . Si suponemos que
. Si suponemos que  tiene dos derivadas continuas (o si consideramos derivados débiles), entonces es posible que utilicemos integración por partes:
tiene dos derivadas continuas (o si consideramos derivados débiles), entonces es posible que utilicemos integración por partes:
con la sustitución
entonces tenemos
pero el primer término es cero, ya que 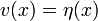 fue elegido para desaparecer en
fue elegido para desaparecer en 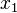 y
y 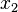 donde se toma la evaluación. Por lo tanto,
donde se toma la evaluación. Por lo tanto,
para cualquier función dos veces diferenciable  que se desvanece en los extremos del intervalo.
que se desvanece en los extremos del intervalo.
Ahora podemos aplicar la lema fundamental del cálculo de variaciones: Si
para cualquier función suficientemente diferenciable  dentro de la gama de integración que se anula en los extremos del intervalo, entonces se deduce que
dentro de la gama de integración que se anula en los extremos del intervalo, entonces se deduce que 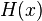 es idénticamente cero en su dominio.
es idénticamente cero en su dominio.
Por lo tanto,
Se desprende de esta ecuación que
y por lo tanto los extremales son líneas rectas.
El Beltrami Identidad
Frecuentemente en problemas físicos, resulta que 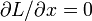 . En ese caso, la ecuación de Euler-Lagrange se puede simplificar usando el Beltrami identidad:
. En ese caso, la ecuación de Euler-Lagrange se puede simplificar usando el Beltrami identidad:
donde  es una constante. El lado izquierdo es el Transformación de Legendre de L con respecto a f '.
es una constante. El lado izquierdo es el Transformación de Legendre de L con respecto a f '.
El teorema de du Bois Reymond
La discusión hasta ahora se ha asumido que las funciones extremales poseen dos derivadas continuas, aunque la existencia de la integral A sólo requiere primero derivadas de las funciones de prueba. La condición de que la primera variación desaparecer en un extremal puede considerarse como una forma débil de la ecuación de Euler-Lagrange. El teorema de du Bois Reymond afirma que esta forma débil implica la forma fuerte. Si L tiene continuas primera y segunda derivada con respecto a todos sus argumentos, y si
entonces 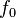 tiene dos derivadas continuas, y se satisface la ecuación de Euler-Lagrange.
tiene dos derivadas continuas, y se satisface la ecuación de Euler-Lagrange.
Funciones de varias variables
Problemas variacionales que involucran integrales múltiples surgen en numerosas aplicaciones. Por ejemplo, si φ (x, y) denota el desplazamiento de una membrana por encima de la de dominio D en el plano x, y, a continuación, su energía potencial es proporcional a su área de superficie:
El problema de la meseta consiste en encontrar una función que minimiza el área de la superficie al tiempo que asume valores prescritos en el límite de D; las soluciones se denominan superficies mínimas. La ecuación de Euler-Lagrange para este problema es no lineal:
Ver Courant (1950) para más detalles.
Principio de Dirichlet
A menudo es suficiente considerar sólo pequeños desplazamientos de la membrana, cuya energía diferencia de desplazamiento no es aproximada
El funcional V debe ser minimizado entre todas las funciones de prueba φ que asumen los valores prescritos en la frontera de D. Si u es la función de minimización y V es una función suave arbitraria que se desvanece en el límite de D, entonces la primera variación de ![V [u + \ epsilon v]](../../images/762/76225.png) debe desaparecer:
debe desaparecer:
A condición de que u tiene dos derivados, podemos aplicar el teorema de la divergencia de obtener
donde C es la frontera de D, s es longitud de arco a lo largo de C y 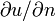 es la derivada normal de U en C. Desde v desvanece en C y la primera variación se desvanece, el resultado es
es la derivada normal de U en C. Desde v desvanece en C y la primera variación se desvanece, el resultado es
Para todas las funciones v suave que desaparece en el límite de D. La prueba para el caso de uno integrales dimensionales puede estar adaptado para este caso para mostrar que
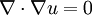 en D.
en D.
La dificultad con este razonamiento es la suposición de que la función de minimización u debe tener dos derivados. Riemann argumentó que la existencia de una función de minimización suave fue asegurado por la conexión con el problema físico:. Membranas de hecho asumen configuraciones de energía potencial mínimo Riemann llamó a esta idea principio de Dirichlet en honor a su maestro Dirichlet. Sin embargo Weierstrass dio un ejemplo de un problema variacional sin solución: reducir al mínimo
entre todas las funciones φ que satisfacen 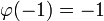 y
y  W puede hacerse arbitrariamente pequeña eligiendo funciones lineales por partes que hacen una transición entre -1 y 1 en un pequeño barrio del origen. Sin embargo, no hay ninguna función que hace que W = 0. La controversia resultante sobre la validez del principio de Dirichlet se explica en http://turnbull.mcs.st-and.ac.uk/~history/Biographies/Riemann.html. Finalmente se muestra que el principio de Dirichlet es válida, pero se requiere una aplicación sofisticada de la teoría de la regularidad de ecuaciones diferenciales parciales elípticas; ver Jost y Li-Jost (1998).
W puede hacerse arbitrariamente pequeña eligiendo funciones lineales por partes que hacen una transición entre -1 y 1 en un pequeño barrio del origen. Sin embargo, no hay ninguna función que hace que W = 0. La controversia resultante sobre la validez del principio de Dirichlet se explica en http://turnbull.mcs.st-and.ac.uk/~history/Biographies/Riemann.html. Finalmente se muestra que el principio de Dirichlet es válida, pero se requiere una aplicación sofisticada de la teoría de la regularidad de ecuaciones diferenciales parciales elípticas; ver Jost y Li-Jost (1998).
La generalización a otros problemas de contorno
Una expresión más general para la energía potencial de una membrana es
Esto corresponde a una densidad fuerza externa  en D, una fuerza externa
en D, una fuerza externa 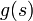 en el límite C, y las fuerzas elásticas con módulo
en el límite C, y las fuerzas elásticas con módulo  actuando en C. La función que minimiza la energía potencial sin restricciones en sus valores límite se denota por u. Siempre que fyg son continuas, la teoría de la regularidad implica que la función de minimización u tendrá dos derivados. Al tomar la primera variación, ninguna condición de frontera tiene que ser impuesta en el incremento v. La primera variación de
actuando en C. La función que minimiza la energía potencial sin restricciones en sus valores límite se denota por u. Siempre que fyg son continuas, la teoría de la regularidad implica que la función de minimización u tendrá dos derivados. Al tomar la primera variación, ninguna condición de frontera tiene que ser impuesta en el incremento v. La primera variación de ![V [u + \ epsilon v]](../../images/762/76225.png) es dado por
es dado por
Si aplicamos el teorema de la divergencia, el resultado es
Si primero establecemos v = 0 en C, la integral de contorno se desvanece, y llegamos a la conclusión que antes de que
en D. Entonces si permitimos v asumir valores límites arbitrarios, esto implica que u debe satisfacer la condición de frontera
en C. Tenga en cuenta que esta condición de frontera es una consecuencia de la propiedad de minimizar u: no se impone de antemano. Tales condiciones se denominan condiciones de contorno naturales.
El razonamiento anterior no es válido si  desaparece de forma idéntica en C. En tal caso, se podría permitir una función de prueba
desaparece de forma idéntica en C. En tal caso, se podría permitir una función de prueba  , Donde c es una constante. Para una función de este tipo de prueba,
, Donde c es una constante. Para una función de este tipo de prueba,
Mediante la elección apropiada de c, V puede asumir cualquier valor menos que la cantidad dentro de los corchetes se desvanece. Por lo tanto el problema variacional tiene sentido a menos
Esta condición implica que las fuerzas externas netas en el sistema están en equilibrio. Si estas fuerzas están en equilibrio, entonces el problema variacional tiene una solución, pero no es único, ya que se puede añadir una constante arbitraria. Más detalles y ejemplos son en Courant y Hilbert (1953).
Problemas de valores propios
Ambos unidimensional problemas de valores propios y multi-dimensionales se pueden formular como problemas variacionales.
Problemas de Sturm-Liouville
El problema de valores propios de Sturm-Liouville implica una forma cuadrática en general
donde φ se limita a las funciones que cumplen las condiciones de contorno
Sea R una normalización integral
Las funciones 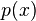 y
y  tienen la obligación de estar en todas partes positiva y acotada lejos de cero. El problema variacional primaria es reducir al mínimo la proporción Q / R entre todos φ satisface las condiciones de punto final. Se muestra a continuación que la ecuación de Euler-Lagrange para la minimización u es
tienen la obligación de estar en todas partes positiva y acotada lejos de cero. El problema variacional primaria es reducir al mínimo la proporción Q / R entre todos φ satisface las condiciones de punto final. Se muestra a continuación que la ecuación de Euler-Lagrange para la minimización u es
donde λ es el cociente
Se puede demostrar (ver Gelfand y Fomin 1963) que la minimización de U tiene dos derivados y satisface la ecuación de Euler-Lagrange. El λ asociado se denota por 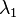 ; es el valor propio más bajo para esta ecuación y las condiciones de contorno. La función de reducción al mínimo asociado se denota por
; es el valor propio más bajo para esta ecuación y las condiciones de contorno. La función de reducción al mínimo asociado se denota por 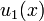 . Esta caracterización variacional de valores propios conduce a la Método de Rayleigh-Ritz: elegir una u aproximan como una combinación lineal de funciones de base (por ejemplo funciones trigonométricas) y llevar a cabo una minimización de dimensión finita entre tales combinaciones lineales. Este método es a menudo sorprendentemente precisa.
. Esta caracterización variacional de valores propios conduce a la Método de Rayleigh-Ritz: elegir una u aproximan como una combinación lineal de funciones de base (por ejemplo funciones trigonométricas) y llevar a cabo una minimización de dimensión finita entre tales combinaciones lineales. Este método es a menudo sorprendentemente precisa.
El siguiente valor propio función propia y más pequeño se pueden obtener mediante la minimización Q bajo la restricción adicional
Este procedimiento se puede ampliar para obtener la secuencia completa de valores propios y las funciones propias para el problema.
El problema variacional también se aplica a las condiciones de contorno más generales. En lugar de exigir que φ se desvanecen en los puntos finales, no puede imponer ninguna condición en los puntos finales, y establecer
donde  y
y 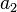 son arbitrarias. Si establecemos
son arbitrarias. Si establecemos 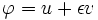 la primera variación de la relación
la primera variación de la relación  es
es
donde λ es dada por el cociente ![Q [u] / R [u]](../../images/762/76259.png) como antes. Después de la integración por partes,
como antes. Después de la integración por partes,
Si primero se requiere que v se desvanecen en los puntos finales, la primera variación se desvanecerá para todos tal v sólo si
Si u satisface esta condición, entonces la primera variación se desvanecerá para v arbitraria sólo si
Estas últimas condiciones son las condiciones de contorno naturales para este problema, ya que no se imponen a funciones de prueba para la reducción, sino que son una consecuencia de la minimización.
Problemas de valores propios en varias dimensiones
Problemas de valores propios en dimensiones más altas se definen en analogía con el caso unidimensional. Por ejemplo, dado un dominio D con frontera B en tres dimensiones podemos definir
y
Sea u la función que minimiza el cociente ![Q [\ varphi] / R [\ phi],](../../images/762/76265.png) sin condición prescrita en el límite B. La ecuación de Euler-Lagrange satisfecho por u es
sin condición prescrita en el límite B. La ecuación de Euler-Lagrange satisfecho por u es
donde
La minimización u también debe satisfacer la condición de frontera natural
en el límite B. Este resultado depende de la teoría de la regularidad de las ecuaciones diferenciales parciales elípticas; ver Jost y Li-Jost (1998) para más detalles. Muchas extensiones, incluyendo los resultados de completitud, propiedades asintóticas de los valores propios y resultados relativos a los nodos de las funciones propias son en Courant y Hilbert (1953).
Aplicaciones
Algunas aplicaciones del Cálculo de variaciones incluyen:
- La derivación de la Forma de catenaria
- La Problema braquistocrona
- Problemas isoperimétricas
- Geodésicas en superficies
- Superficies mínimas y Problema de Plateau
- Control Óptimo
El principio de Fermat
Estados principio de Fermat que la luz toma un camino que (a nivel local) minimiza la longitud óptica entre sus puntos extremos. Si la coordenada x es elegido como el parámetro a lo largo del camino, y 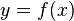 a lo largo del camino, entonces la longitud óptica está dada por
a lo largo del camino, entonces la longitud óptica está dada por
donde el índice de refracción  depende del material. Si tratamos
depende del material. Si tratamos 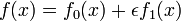 entonces la primera variación de A (la derivada de A con respecto a ε) es
entonces la primera variación de A (la derivada de A con respecto a ε) es
Después de la integración por partes del primer término entre paréntesis, se obtiene la ecuación de Euler-Lagrange
Los rayos de luz se pueden determinar mediante la integración de esta ecuación.
La ley de Snell
Hay una discontinuidad del índice de refracción cuando la luz entra o sale de una lente. Dejar
donde  y
y 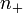 son constantes. Entonces la ecuación de Euler-Lagrange tiene como antes en la región donde x <0 o x> 0, y de hecho la ruta de acceso es una línea recta allí, ya que el índice de refracción es constante. Al x = 0, f debe ser continua, pero f 'puede ser discontinua. Después de la integración por partes de las regiones separadas y utilizando las ecuaciones de Euler-Lagrange, la primera variación toma la forma
son constantes. Entonces la ecuación de Euler-Lagrange tiene como antes en la región donde x <0 o x> 0, y de hecho la ruta de acceso es una línea recta allí, ya que el índice de refracción es constante. Al x = 0, f debe ser continua, pero f 'puede ser discontinua. Después de la integración por partes de las regiones separadas y utilizando las ecuaciones de Euler-Lagrange, la primera variación toma la forma
El factor multiplicador  es el seno del ángulo del rayo incidente con el eje x, y el factor multiplicador
es el seno del ángulo del rayo incidente con el eje x, y el factor multiplicador 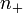 es el seno del ángulo del rayo refractado con el eje x. La ley de Snell de la refracción requiere que estas condiciones sean iguales. Como este cálculo demuestra, la ley de Snell es equivalente a la desaparición de la primera variación de la longitud del camino óptico.
es el seno del ángulo del rayo refractado con el eje x. La ley de Snell de la refracción requiere que estas condiciones sean iguales. Como este cálculo demuestra, la ley de Snell es equivalente a la desaparición de la primera variación de la longitud del camino óptico.
El principio de Fermat en tres dimensiones
Es conveniente utilizar la notación vectorial: dejar 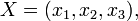 sea t un parámetro, vamos
sea t un parámetro, vamos  ser la representación paramétrica de una curva C, y dejar
ser la representación paramétrica de una curva C, y dejar 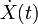 ser su vector tangente. La longitud óptica de la curva está dada por
ser su vector tangente. La longitud óptica de la curva está dada por
Tenga en cuenta que esta integral es invariante con respecto a los cambios en la representación paramétrica de C. Las ecuaciones de Euler-Lagrange para una curva de minimizar tienen la forma simétrica
donde
Se desprende de la definición que satisfaga P
Por lo tanto la integral también se puede escribir como
Esta forma sugiere que si podemos encontrar una ψ función cuyo gradiente está dada por P, luego la A integral está dada por la diferencia de ψ en los extremos del intervalo de integración. Así, el problema de estudiar las curvas que hacen que el estacionaria integral puede estar relacionado con el estudio de las superficies de nivel de ψ. Con el fin de encontrar una función de este tipo, nos volvemos a la ecuación de onda, que regula la propagación de la luz.
Conexión con la ecuación de onda
La ecuación de onda para un medio no homogéneo es
donde c es la velocidad, que generalmente depende de X. Frentes de onda de la luz son superficies característicos de esta ecuación diferencial parcial: satisfacen
Podemos buscar soluciones en forma
En ese caso, satisface ψ
donde  De acuerdo con la teoría de la de primer orden ecuaciones diferenciales parciales, si
De acuerdo con la teoría de la de primer orden ecuaciones diferenciales parciales, si  entonces satisface P
entonces satisface P
a lo largo de un sistema de curvas (los rayos de luz) que se dan por
Estas ecuaciones para la solución de una ecuación diferencial parcial de primer orden son idénticas a las ecuaciones de Euler-Lagrange si hacemos la identificación
Llegamos a la conclusión de que la función ψ es el valor de la minimización de una integral como una función del punto de extremo superior. Es decir, cuando se construye una familia de curvas minimizar, los valores de la longitud óptica satisfacen la ecuación característica correspondiente de la ecuación de onda. Por lo tanto, la solución de la ecuación diferencial parcial asociado de primer orden es equivalente a encontrar familias de soluciones del problema variacional. Este es el contenido esencial de la Teoría de Hamilton-Jacobi, que se aplica a los problemas variacionales más generales.
El principio de acción
La acción fue definido por Hamilton ser la integral en el tiempo de la función de Lagrange, L, que se define como una diferencia de energías:
donde T es la energía cinética de un sistema mecánico y U es la energía potencial. El principio de Hamilton (o el principio de acción) afirma que el movimiento de un holonómicas conservadores (limitaciones integrables) sistema mecánico es tal que la acción integral
es estacionario con respecto a las variaciones en la trayectoria x (t). Las ecuaciones de Euler-Lagrange para este sistema se conocen como las ecuaciones de Lagrange:
y que son equivalentes a las ecuaciones de Newton del movimiento (para tales sistemas).
La momentos conjugados P se definen por
Por ejemplo, si
entonces
Mecánica hamiltoniana resultados si el momentos conjugados se introducen en el lugar de 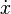 Y la L de Lagrange se sustituye por el hamiltoniano H definido por
Y la L de Lagrange se sustituye por el hamiltoniano H definido por
El hamiltoniano es la energía total del sistema: H = T + T. Analogía con el principio de Fermat sugiere que las soluciones de las ecuaciones de Lagrange (las trayectorias de las partículas) se puede describir en términos de superficies de nivel de una función de x. Esta función es una solución de la Hamilton-Jacobi ecuación:
![A [f] = \ int_ {x_1} ^ {x_2} L (x, f, f ') \, dx. \,](../../images/761/76191.png)
![A [F_0] \ le A [F_0 + \ epsilon \ eta]](../../images/761/76196.png)

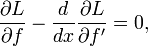
![A [f] = \ int_ {x_1} ^ {x_2} \ sqrt {1 + [f '(x)] ^ 2} \, dx,](../../images/762/76203.png)
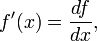
![\ Int_ {x_1} ^ {x_2} \ frac {F_0 '(x) \ eta' (x)} {\ sqrt {1 + [F_0 '(x)] ^ 2}} \, dx = 0, \,](../../images/762/76208.png)
![\ Int_a ^ bu (x) \ eta '(x) \, dx = \ left [u (x) \ eta (x) \ right] _ {a} ^ {b} - \ int_a ^ b u' (x) \ eta (x) \, dx](../../images/762/76210.png)
![u (x) = \ frac {F_0 '(x)} {\ sqrt {1 + [F_0' (x)] ^ 2}}](../../images/762/76211.png)
![\ Left [u (x) \ eta (x) \ right] _ {x_1} ^ {x_2} - \ int_ {x_1} ^ {x_2} \ eta (x) \ frac {d} {dx} \ left [\ frac {F_0 '(x)} {\ sqrt {1 + [F_0' (x)] ^ 2}} \ right] \, dx = 0,](../../images/762/76212.png)
![\ Int_ {x_1} ^ {x_2} \ eta (x) \ frac {d} {dx} \ left [\ frac {F_0 '(x)} {\ sqrt {1 + [F_0' (x)] ^ 2} } \ right] \, dx = 0](../../images/762/76214.png)
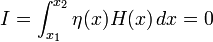
![\ Frac {d} {dx} \ left [\ frac {F_0 '(x)} {\ sqrt {1 + [F_0' (x)] ^ 2}} \ right] = 0. \,](../../images/762/76217.png)



![U [\ varphi] = \ iint_D \ sqrt {1 + \ nabla \ phi \ cdot \ nabla \ phi} dx \, dy. \,](../../images/762/76222.png)
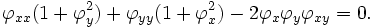
![V [\ varphi] = \ frac {1} {2} \ iint_D \ nabla \ phi \ cdot \ nabla \ phi \, dx \, dy. \,](../../images/762/76224.png)
![\ Frac {d} {d \ epsilon} V [u + \ epsilon v] | _ {\ epsilon = 0} = \ iint_D \ nabla u \ cdot \ nabla v \, dx \, dy = 0. \,](../../images/762/76226.png)
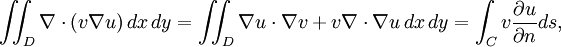
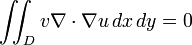
![W [\ varphi] = \ int _ {- 1} ^ {1} (x \ phi ') ^ 2 \, dx \,](../../images/762/76231.png)
![V [\ varphi] = \ iint_D \ left [\ frac {1} {2} \ nabla \ phi \ cdot \ nabla \ phi + f (x, y) \ phi \ right] \, dx \, dy \, + \ int_C \ left [\ frac {1} {2} \ sigma (s) \ phi ^ 2 + g (s) \ phi \ right] \, ds.](../../images/762/76234.png)
![\ Iint_D \ left [\ nabla u \ cdot \ nabla v + fv \ right] \, dx \, dy + \ int_C \ left [\ sigma uv + gv \ right] \, ds = 0. \,](../../images/762/76238.png)
![\ Iint_D \ left [-v \ nabla \ cdot \ nabla u + vf \ right] \, dx \, dy + \ int_C v \ left [\ frac {\ part u} {\ part n} + \ sigma u + g \ right] \, ds = 0. \,](../../images/762/76239.png)
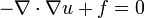
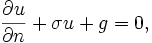
![V [c] = c \ left [\ iint_D f \, dx \, dy + \ int_C g ds \ right].](../../images/762/76243.png)
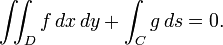
![Q [\ varphi] = \ int_ {x_1} ^ {x_2} \ left [p (x) \ phi '(x) ^ 2 + q (x) \ phi (x) ^ 2 \ right] \, dx, \ ,](../../images/762/76245.png)

![R [\ varphi] = \ int_ {x_1} ^ {x_2} r (x) \ varphi (x) ^ 2 \, dx \.,](../../images/762/76247.png)

![\ Lambda = \ frac {Q [u]} {R [u]}. \,](../../images/762/76251.png)

![Q [\ varphi] = \ int_ {x_1} ^ {x_2} \ left [p (x) \ phi '(x) ^ 2 + q (x) \ phi (x) ^ 2 \ right] \, dx + a_1 \ phi (x 1) ^ 2 + a_2 \ phi (x_2) ^ 2, \,](../../images/762/76255.png)
![V_1 = \ frac {2} {R [u]} \ left (\ int_ {x_1} ^ {x_2} \ left [p (x) u '(x) v' (x) + q (x) u (x ) v (x) - \ lambda u (x) v (x) \ right] \, dx + a_1 u (x 1) v (x 1) + a_2 u (x_2) v (x_2) \ right), \,](../../images/762/76258.png)
![\ Frac {R [u]} {2} V_1 = \ int_ {x_1} ^ {x_2} v (x) \ left [- (p u ')' + qu - \ lambda ru \ right] \, dx + v (x 1) [-p (x_1) u '(x 1) + a_1 u (x 1)] + v (x_2) [p (x_2 u' (x_2) + a_2 u (x_2). \,](../../images/762/76260.png)


![Q [\ varphi] = \ iiint_D p (X) \ nabla \ phi \ cdot \ nabla \ phi + q (X) \ phi ^ 2 \, dx \, dy \, dz + \ iint_B \ sigma (S) \ varphi ^ 2 \, DS, \,](../../images/762/76263.png)
![R [\ varphi] = \ iiint_D r (X) \ varphi (X) ^ 2 \, dx \, dy \, dz. \,](../../images/762/76264.png)
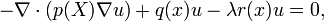
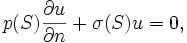
![A [f] = \ int_ {x = x 0} ^ {x_1} n (x, f (x)) \ sqrt {1 + f '(x) ^ 2} dx, \,](../../images/762/76268.png)
![\ Delta A [F_0, f_1] = \ int_ {x = x 0} ^ {x_1} \ left [\ frac {n (x, F_0) F_0 '(x) f_1' (x)} {\ sqrt {1 + F_0 '(x) ^ 2}} + n_y (x, F_0) f_1 \ sqrt {1 + F_0' (x) ^ 2} \ right] dx.](../../images/762/76271.png)
![- \ Frac {d} {dx} \ left [\ frac {n (x, F_0) F_0 '} {\ sqrt {1 + F_0' ^ 2}} \ right] + n_y (x, F_0) \ sqrt {1 + F_0 '(x) ^ 2} = 0. \,](../../images/762/76272.png)
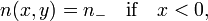

![\ Delta A [F_0, f_1] = f_1 (0) \ left [n _- \ frac {F_0 '(0 _-)} {\ sqrt {1 + F_0' (0 _-) ^ 2}} -n _ + \ frac { F_0 '(0 _ +)} {\ sqrt {1 + F_0' (0 _ +) ^ 2}} \ right]. \,](../../images/762/76277.png)
![A [C] = \ int_ {t = t_0} ^ {} t_1 n (X) \ sqrt {\ dot X \ cdot \ dot X} dt. \,](../../images/762/76281.png)

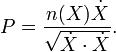
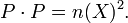
![A [C] = \ int_ {t = t_0} ^ {t_1} P \ cdot \ dot X \, dt \.,](../../images/762/76285.png)
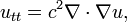

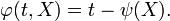
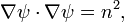
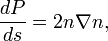
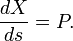

![A [C] = \ int_ {t = t_0} ^ {t_1} L (x, \ dot x, t) dt \,](../../images/762/76296.png)