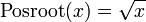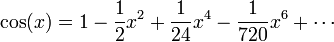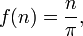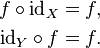Función (matemáticas)
Antecedentes de las escuelas de Wikipedia
Esta selección se hace para las escuelas por caridad para niños leer más . Una rápida conexión para el apadrinamiento de niños es http://www.sponsor-a-child.org.uk/
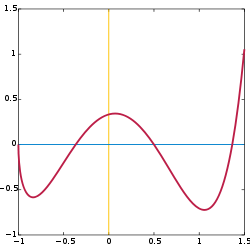
![\ Begin {align} y \ scriptstyle f \ de colon [-1,1.5] \ a [-1,1.5] \\ & \ estilo de texto x \ mapsto \ frac {(4x ^ 3-6x ^ 2 + 1) \ sqrt { x + 1}} {3-x} \ end {align}](../../images/121/12113.png)
La matemática concepto de una función expresa la dependencia entre dos cantidades, una de las cuales se da (el variable independiente, el argumento de la función, o su "entrada") y el otro producido (la variable dependiente, el valor de la función, o "salida"). Una función asocia una sola salida a cada elemento de entrada extraída de un fijo establecer, como los números reales .
Hay muchas maneras de dar una función: por una fórmula , por una trama o gráfica, por un algoritmo que calcula que, por una descripción de sus propiedades. A veces, una función se describe a través de su relación con otras funciones (véase, por ejemplo, función inversa ). En disciplinas aplicadas, las funciones se especifican con frecuencia por sus tablas de valores o por una fórmula. No todos los tipos de descripción se pueden dar para cada función sea posible, y hay que hacer una clara distinción entre la función en sí y múltiples formas de presentar o visualizarlo.
Una idea de enorme importancia en toda la matemática es la composición de funciones : si z es una función de Y e Y es una función de x, entonces z es una función de x. Podemos describir informalmente diciendo que la función compuesta se obtiene mediante el uso de la salida de la primera función que la entrada de la segunda. Esta característica de las funciones que los distingue de otras construcciones matemáticas, tales como números o figuras, y proporciona la teoría de funciones con su más poderosa estructura.
Introducción
Funciones desempeñan un papel fundamental en todas las áreas de las matemáticas, así como en otras ciencias y la ingeniería. Sin embargo, la intuición relacionada con las funciones, notación, e incluso el propio significado del término "función" varía entre los campos. Más áreas abstractas de las matemáticas, como la teoría de conjuntos , consideran tipos muy generales de las funciones, las cuales no pueden ser especificados por una regla concreta y no se rigen por ningún principio conocidos. La propiedad característica de una función en el sentido más abstracto es que se refiere exactamente una salida a cada una de sus entradas admisibles. Tales funciones no tienen que implican números y pueden, por ejemplo, asociar cada uno de un conjunto de palabras con sus propias primeras letras.
Funciones en el álgebra son generalmente expresable en términos de operaciones algebraicas. Funciones estudiadas en el análisis , como por ejemplo la función exponencial , pueden tener propiedades adicionales derivados de la continuidad del espacio, pero en el caso más general no pueden ser definidos por una sola fórmula. Las funciones analíticas en análisis complejo puede definirse bastante concretamente a través de su desarrollos en serie. Por otro lado, en cálculo lambda, la función es un concepto primitivo, en lugar de ser definido en términos de la teoría de conjuntos. Los términos la transformación y mapeo son a menudo sinónimo de función. En algunos contextos, sin embargo, difieren ligeramente. En el primer caso, la transformación término se aplica generalmente a las funciones cuyas entradas y salidas son elementos del mismo conjunto o estructura más general. Por lo tanto, hablamos de transformaciones lineales de un espacio vectorial en sí mismo y de simetría transformaciones de un objeto geométrico o un patrón. En el segundo caso, que se utiliza para describir conjuntos cuya naturaleza es arbitraria, el mapeo plazo es el concepto más general de la función.
Las funciones matemáticas se denotan con frecuencia por letras, y la notación estándar para la salida de una función f con la entrada x es ƒ (x). Una función puede ser definida sólo para ciertos insumos, y la colección de todas las entradas aceptables de la función se llama su dominio. El conjunto de todos los productos resultantes se denomina rango de la función. Sin embargo, en muchos campos, también es importante para especificar la codominio de una función, con la serie, pero no tiene que ser igual a ella. La distinción entre gama y codominio nos hace preguntarnos si los dos pasan a ser igual, que en determinados casos puede ser una cuestión de cierto interés matemático.
Por ejemplo, la expresión ƒ (x) = x 2 describe una función f de una variable X, que, dependiendo del contexto, puede ser un número entero , un verdadero o complejo número o incluso un elemento de un grupo . Precisemos que x es un número entero; a continuación, esta función se refiere cada entrada, x, con una sola salida, x 2, obtenido a partir de x por cuadratura. Por lo tanto, la entrada de 3 está relacionado con la salida de 9, la entrada de 1 a la salida de 1, y la entrada de -2 a la salida de 4, y escribir ƒ (3) = 9, ƒ (1) = 1, ƒ (-2) = 4. Debido a que cada número entero puede ser cuadrado, el dominio de esta función consiste en todos los números enteros, mientras que su rango es el conjunto de cuadrados perfectos. Si elegimos enteros como el codominio, así, nos encontramos con que muchos números, como el 2, 3 y 6, están en el codominio pero no el rango.
Es una práctica habitual en las matemáticas para introducir funciones con nombres temporales como ƒ; en el siguiente párrafo que podríamos definir f (x) = 2 x 1, y luego f (3) = 7. Cuando no se necesita el nombre de la función, se utiliza a menudo la forma y = x 2.
Si utilizamos una función a menudo, podemos darle un nombre más permanente como, por ejemplo,
La propiedad esencial de una función es que para cada entrada debe haber una salida única. Así, por ejemplo, la fórmula
no define una función de una variable real positivo, porque asigna dos salidas a cada número: las raíces cuadradas de 9 son 3 y -3. Para hacer la raíz cuadrada de una función, debemos especificar que la raíz cuadrada para elegir. La definición
para cualquier entrada positiva elige la raíz cuadrada positiva como una salida.
Como se mencionó anteriormente, una función no tiene por qué implicar números. A modo de ejemplos, considere la función que asocia con cada palabra su primera carta o la función que se asocia con cada triángulo su área.
Definiciones
Dado que las funciones se utilizan en muchas áreas de las matemáticas, y de muchas maneras diferentes, hay una definición única de la función ha sido adoptado universalmente. Algunas definiciones son elementales, mientras que otros utilizan un lenguaje técnico que pueden oscurecer la noción intuitiva. Sin embargo, la idea fundamental es la misma en cada definición.
Una definición elemental es que
- Una función está dada por una expresión aritmética que describe cómo un número depende de otro.
Un ejemplo de tal función es y = 5 x 3 x 16 -20 x 5, donde el valor de y depende del valor de x. Esto es enteramente satisfactoria para las partes de la matemática elemental, pero es demasiado torpe y restrictiva para las áreas más avanzadas. Por ejemplo, el coseno función utilizada en la trigonometría no se puede escribir de esta manera; lo mejor que podemos hacer es un serie infinita,
Dicho esto, si estamos dispuestos a aceptar la serie como un sentido amplio de "expresión aritmética", tenemos una definición que sirvió matemáticas razonablemente bien durante cientos de años.
Con el tiempo la transformación gradual de "cálculo" intuitivo en el "análisis" formal trajo la necesidad de una definición más amplia. El énfasis pasó de cómo se presentó una función - como una fórmula o regla - a un concepto más abstracto. Parte de la nueva fundación fue el uso de juegos , por lo que las funciones ya no se limitan a los números. Por lo tanto podemos decir que
- Una función f de un conjunto X a un conjunto Y asociados a cada elemento x en un elemento X y = ƒ (x) en Y.
Ten en cuenta que X e Y no tiene por qué ser diferentes conjuntos; es posible tener una función de un conjunto a sí mismo. Aunque es posible interpretar el término "asociados" en esta definición con una regla concreta para la asociación, es esencial ir más allá de esa restricción. Por ejemplo, a veces se puede demostrar que existe una función con ciertas propiedades, sin embargo, no seamos capaces de dar ninguna regla explícita para la asociación. De hecho, en algunos casos es imposible dar una regla explícita producir una y específico para cada x, a pesar de que existe tal función. En el contexto de las funciones definidas en conjuntos arbitrarios, ni siquiera es claro cómo se debe interpretar la frase "regla explícita".
Como funciones asumen nuevos roles y encontrar nuevos usos, la relación de la función de los conjuntos requiere más precisión. Tal vez cada elemento en Y se asocia con algunas x, tal vez no. En algunas partes de las matemáticas, incluyendo teoría de la repetición y análisis funcional, es conveniente permitir que los valores de x con ninguna asociación (en este caso, el término función parcial se utiliza a menudo). Para poder hablar de este tipo de distinciones, muchos autores dividieron una función en tres partes, cada una de un conjunto:
- Una función f es un triple ordenada de conjuntos (F, X, Y) con restricciones, donde
- F (el gráfico) es un conjunto de pares ordenados (x, y),
- X (la fuente) contiene todos los primeros elementos de F y tal vez más, y
- Y (el objetivo) contiene todos los segundos elementos de F y tal vez más.
Las restricciones más comunes son que f pares cada X con un solo y, y que X es sólo el conjunto de primeros elementos de F y no más.
Cuando se colocan restricciones en F, hablamos de una relación entre X e Y en lugar de una función. La relación es "de un solo valor" cuando la primera restricción tiene: (x, y 1) ∈ F y (x, y 2) ∈ F juntos implica y 1 = y 2. Relaciones que no son valoradas solo a veces se llaman funciones multiformes. Una relación es "total" cuando una segunda restricción sostiene: si x ∈ X entonces (x, y) ∈ F para algunos y. Así también podemos decir que
- Una función de X a Y es un valor único relación, total entre X e Y.
La gama de F, y de ƒ, es el conjunto de todos los segundos elementos de F; a menudo se denota por ƒ rng. El dominio de f es el conjunto de todos los primeros elementos de F; a menudo se denota por ƒ dom. Hay dos definiciones comunes para el dominio de ƒ algunos autores lo definen como el dominio de F, mientras que otros lo definen como la fuente de F.
El objetivo de ƒ Y también se llama el codominio de f, denotada por ƒ bacalao; y la gama de ƒ también se llama la imagen de ƒ, denotado por im ƒ. El ƒ notación: X → Y indica que ƒ es una función con dominio X y Y codominio.
Algunos autores omiten el origen y el destino como datos innecesarios. De hecho, dada sólo el gráfico F, se puede construir un triple adecuado tomando dom F a ser la fuente y rng F a ser el blanco; esto hace que automáticamente F a ser total. Sin embargo, la mayoría de los autores en las matemáticas avanzadas prefieren el mayor poder de expresión que ofrece el triple, especialmente la distinción que permite entre rango y codominio.
Por cierto, los pares y triples ordenados que hemos utilizado no son distintos de los conjuntos; podemos representar fácilmente dentro de la teoría de conjuntos. Por ejemplo, podemos utilizar {{x}, {x, y}} para el par (x, y). Entonces, para un triple (x, y, z) podemos utilizar el par ((x, y), z). Una construcción importante es la Producto cartesiano de los conjuntos de X y Y, denotado por X × Y, que es el conjunto de todos los posibles pares ordenados (x, y) con x ∈ X y y ∈ Y. También podemos construir el conjunto de todas las funciones posibles del conjunto X al conjunto Y, que denotamos por cualquiera [X → Y] o Y X.
Ahora tenemos una gran flexibilidad. Mediante el uso de pares de X podemos tratar, por ejemplo, la resta de números enteros como una función, sub: Z × Z → Z. Mediante el uso de pares para Y podemos dibujar una curva plana utilizando una función, crv: R → R × R. En el intervalo de la unidad, yo, que puedo tener una función definida como uno de los números racionales y cero en caso contrario, rata: I → 2. Mediante el uso de las funciones de X podemos considerar una integral definida sobre el intervalo unidad a ser una función, int: [I → R] → R.
Sin embargo, todavía no estamos satisfechos. Podemos queremos aún más generalidad, como una función cuya integral es un función de paso; por tanto, definimos la llamada funciones generalizadas. Podemos querer menos generalidad, como una función que siempre se puede utilizar realmente para obtener una respuesta definitiva; así definimos funciones recursivas primitivas y luego limitarnos a los que podemos probar son efectivamente computable. O podemos querer relacionarse no sólo establece, pero las estructuras algebraicas , con operaciones; así definimos homomorfismos.
Historia
La historia del concepto de función matemática se describe por da Ponte (1992). Como un término matemático ", función" fue acuñado por Gottfried Leibniz en 1694, para describir una cantidad relacionada con una curva , como una curva de pendiente en un específica punto. Las funciones Leibniz considera son hoy llamado funciones diferenciables . Para este tipo de función, se puede hablar de límites y derivados ; ambos son mediciones de la salida o el cambio en la salida ya que depende de la entrada o el cambio en la entrada. Tales funciones son la base de cálculo .
La función de la palabra fue utilizado después por Leonhard Euler en el siglo de mid-18th para describir un expresión o fórmula que involucra diversos argumentos, por ejemplo, f (x) = sin (x) + x 3.
Durante el siglo 19, los matemáticos empezaron a formalizar todas las diferentes ramas de las matemáticas. Weierstrass abogó por la construcción de cálculos en aritmética , más que en la geometría , lo que favoreció la definición de Euler sobre Leibniz (ver aritmetización de análisis).
Al principio, la idea de una función era bastante limitado. Joseph Fourier, por ejemplo, se reivindica que cada función tenía una Series de Fourier, algo que ningún matemático reclamaría hoy. Al ampliar la definición de funciones, los matemáticos pudieron estudiar "extraños" objetos matemáticos como funciones continuas que son ninguna parte diferenciable. Estas funciones se pensó primero en ser sólo curiosidades teóricas, y se denominan colectivamente "monstruos" tan tarde como en la vuelta del siglo 20. Técnicas Sin embargo, poderosos desde análisis funcional han demostrado que estas funciones son en cierto sentido "más comunes" de funciones diferenciables. Tales funciones ya se han aplicado a la modelización de fenómenos físicos tales como El movimiento browniano.
Hacia el final del siglo 19, los matemáticos empezaron a formalizar toda la matemática utilizando la teoría de conjuntos , y trataron de definir cada objeto matemático como establecer. Dirichlet y Lobachevsky tradicionalmente se le atribuye de forma independiente dando la definición moderna "formal" de una función como una relación en la que cada primer elemento tiene un segundo elemento único, pero la afirmación de Dirichlet a esta formalización es disputada por Imre Lakatos:
- No hay tal definición en los trabajos de Dirichlet en absoluto. Pero hay amplia evidencia de que no tenía ni idea de este concepto. En su [1837], por ejemplo, cuando habla de las funciones continuas a trozos, dice que en los puntos de discontinuidad de la función tiene dos valores: ...
- (Pruebas y refutaciones, 151, Cambridge University Press 1976)
Hardy (1908, pp. 26-28) define una función como una relación entre dos variables x e y tales que "para algunos valores de x en cualquier tasa corresponde valores de y." Él ni se requiere la función que se define para todos los valores de x ni para asociar cada valor de x para un solo valor de y. Esta amplia definición de una función abarca más relaciones que normalmente se consideran funciones en la matemática contemporánea.
La noción de una función como una regla para la computación, en lugar de un tipo especial de relación, ha sido ampliamente estudiado en y la lógica matemática la informática teórica. Modelos para éstos funciones computables incluyen la cálculo lambda, el funciones μ-recursivas y Máquinas de Turing.
Vocabulario
Una entrada específica en una función se llama un argumento de la función. Para cada valor del argumento x, el correspondiente y único en el codominio es llamado el valor de la función en x, o el imagen de x bajo ƒ. La imagen de x se puede escribir como ƒ (x) o como y. (Vea la sección de notación .)
La gráfica de una función f es el conjunto de todos pares ordenados (x, f (x)), para todo x en el dominio X. Si X e Y son subconjuntos de R, los números reales, entonces esta definición coincide con el sentido familiar de "graph" como una imagen o representación gráfica de la función, con los pares ordenados siendo las coordenadas cartesianas de puntos.
El concepto de la imagen se puede extender desde la imagen de un punto a la imagen de una establecer. Si A es cualquier subconjunto del dominio, entonces f (A) es el subconjunto de la gama que consta de todas las imágenes de elementos de A. Nos dicen que el ƒ (A) es la imagen de un bajo f.
Observe que la gama de ƒ ƒ es la imagen (X) de su dominio, y que la gama de ƒ es un subconjunto de su codomain.
La preimagen (o imagen inversa, o más precisamente, la imagen inversa completa) de un subconjunto B de la codomain Y bajo una función f es el subconjunto del dominio X definido por
Así, por ejemplo, la imagen inversa de {4, 9} bajo la función de elevación al cuadrado es el conjunto {-3, -2, + 2, + 3}.
En general, la imagen inversa de una conjunto unitario (un conjunto con exactamente un elemento) puede contener cualquier número de elementos. Por ejemplo, si f (x) = 7, entonces la imagen inversa de {5} es el conjunto vacío, pero el preimagen de {7} es todo el dominio. Así, la imagen inversa de un elemento en la codomain es un subconjunto del dominio. La convención usual sobre la imagen inversa de un elemento es que ƒ -1 (b) significa ƒ -1 ({b}), es decir,
Tres tipos importantes de la función son los inyecciones (o uno-a-uno funciones), que tienen la propiedad de que si f (a) = f (b), entonces una necesidad igual a b; la surjections (o en funciones), que tienen la propiedad de que para cada y en el codomain hay una x en el dominio tal que f (x) = y; y la biyecciones, que son tanto uno a uno y sobre. Esta nomenclatura fue presentado por el Grupo Bourbaki.
Cuando se utiliza la primera definición de la función dada anteriormente, ya que el codominio no está definido, el "surjection" debe ir acompañado de una declaración sobre el conjunto de la función de los mapas en. Por ejemplo, podríamos decir mapas ƒ en el conjunto de todos los números reales.
Restricciones y extensiones
Informalmente, un restricción de una función f es el resultado de recorte de su dominio.
Más precisamente, si ƒ es una función de una X a Y, y S es cualquier subconjunto de X, la restricción de ƒ para S es la función f | S de S a Y tal que ƒ | S (S) = ƒ (s ) para todo s en S.
Si g es cualquier restricción de ƒ, decimos que ƒ es una extensión de g.
Notación
Es común omitir los paréntesis alrededor del argumento cuando hay pocas posibilidades de ambigüedad, por lo tanto: sen x. En algunos contextos formales, el uso de notación polaca inversa, x ƒ, elimina la necesidad de cualquier paréntesis; y, por ejemplo, el factorial función siempre se escribe n!, aunque su generalización, la función gamma, se escribe Γ (n).
Descripción formal de una función típicamente implica el nombre de la función, su dominio, su codominio, y una regla de correspondencia. Por lo tanto vemos con frecuencia una anotación de dos partes, siendo un ejemplo
donde la primera parte se lee:
- "Ƒ es una función de N a R" (uno escribe a menudo informalmente "Que ƒ: X → Y" para significar "Vamos ƒ ser una función de X a Y"), o
- "Ƒ es una función de N en R", o
- "Ƒ es una función de R -valued de un N -valued variable",
y la segunda parte se lee:
 mapas a
mapas a 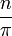
Aquí la función llamada "ƒ" tiene los números naturales como dominio, los números reales como codominio, y mapas n a sí dividida por π. Menos formalmente, esta forma de largo podría ser abreviada
aunque con alguna pérdida de información; ya no da explícitamente el dominio y codominio. Incluso la forma larga abrevia aquí el hecho de que la n en el lado derecho se trata en silencio como un número real usando la incrustación estándar.
Una alternativa a la notación de colon, conveniente cuando las funciones están siendo formados, escribe el nombre de la función por encima de la flecha. Por ejemplo, si ƒ es seguido por g, donde g produce el número complejo e i x, podemos escribir
Una forma más elaborada de esto es el diagrama conmutativo.
El uso de ƒ (A), que indica la imagen de un subconjunto A ⊆ X es consistente siempre que ningún subconjunto del dominio es también un elemento del dominio. En algunos campos (por ejemplo, en la teoría de conjuntos, donde ordinales son también establece de ordinales) es conveniente o incluso necesario distinguir los dos conceptos; la notación habitual es ƒ [A] para el conjunto {f (x): x ∈ A}; algunos autores escriben ƒ` x en lugar de ƒ (x), y ƒ`` A en lugar de ƒ [A].
Tipo de función
La composición de la función de dos o más funciones utiliza la salida de una función como la entrada de otro. Por ejemplo, f (x) = sin (x 2) es la composición de la función seno y la función de elevación al cuadrado. Las funciones ƒ: X → Y y G: Y → Z pueden estar compuestas mediante la aplicación de primera ƒ a un argumento x para obtener y = ƒ (x) y luego aplicando g a Y para obtener z = g (y). La función compuesto formado de esta manera de lo general g ƒ y puede ser escrito
La función de la derecha actúa primero y la función de la izquierda actúa segundo, invirtiendo el orden de lectura Inglés. Recordamos el orden mediante la lectura de la notación como "g de ƒ". El orden es importante, porque raramente obtenemos el mismo resultado en ambos sentidos. Por ejemplo, supongamos que f (x) = x 2 y g (x) = x +1. Entonces g (ƒ (x)) = x 2 1, mientras que f (g (x)) = (x 1) 2, que es 2 x 2 x 1, una función diferente.
Función Identidad
La función única sobre un conjunto X que proyecta cada elemento de sí mismo se llama la función identidad para X, y por lo general denota por id X. Cada conjunto tiene su propia función de identidad, por lo que el subíndice no puede ser omitido a menos que el conjunto se puede inferir a partir del contexto. Bajo composición, una función de identidad es "neutral": si ƒ es cualquier función de X a Y, entonces
Función inversa
Si ƒ es una función de X a Y a continuación, una función inversa para ƒ, denotado por ƒ -1, es una función en la dirección opuesta, de Y a X, con la propiedad de que una ida y vuelta (una composición ) devuelve cada elemento sí mismo. No todas las funciones tiene un inverso; los que lo hacen son llamados invertible.
Como un ejemplo sencillo, si ƒ convierte una temperatura en grados Celsius a grados Fahrenheit, la función de conversión de grados Fahrenheit a grados Celsius sería un -1 ƒ adecuado.
La notación para la composición nos recuerda la multiplicación; de hecho, a veces lo denotamos mediante la yuxtaposición, g ƒ, sin un círculo intermedio. Bajo esta analogía, las funciones de identidad son como 1, e inversas son como recíprocos (de ahí la notación).
Especificación de una función
Una función puede ser definido por cualquier condición matemática que relaciona cada argumento con el valor de salida correspondiente. Si el dominio es finito, un ƒ función se puede definir simplemente tabular todos los argumentos x y sus correspondientes valores de la función ƒ (x). Más comúnmente, una función está definida por una fórmula , o (en general) un algoritmo de - una receta que indica cómo calcular el valor de f (x) dado cualquier x en el dominio.
Hay muchas otras maneras de definir funciones. Los ejemplos incluyen recursividad, algebraica o analítico cierre, límites , continuación analítica, infinito serie, y como soluciones a integrales y ecuaciones diferenciales . La cálculo lambda ofrece una potente y flexible sintaxis para la definición y la combinación de funciones de varias variables.
Computabilidad
Funciones que envían números enteros a enteros, o cadenas finitas de cadenas finitas, a veces puede ser definido por un algoritmo , lo que da una descripción precisa de un conjunto de pasos para calcular la salida de la función a partir de su entrada. Funciones definibles por un algoritmo se llaman funciones computables. Por ejemplo, el Algoritmo de Euclides da un proceso preciso para calcular el máximo común divisor de dos enteros positivos. Muchas de las funciones estudiadas en el contexto de la teoría de números son computables.
Resultados Fundamentales de teoría de la computabilidad muestran que hay funciones que se pueden definir con precisión, pero no son computables. Por otra parte, en el sentido de cardinalidad, casi todas las funciones de los enteros a enteros no son computables. El número de funciones computables a partir de números enteros a enteros es contable, porque el número de posibles algoritmos es. El número de todas las funciones de números enteros a números enteros es más alto: la misma que la cardinalidad de los números reales . Así, la mayoría de las funciones de números enteros a enteros no son computables. Los ejemplos específicos de funciones no computables son conocidos, incluyendo el función castor ocupado y funciones relacionadas con la problema de la parada y otra problemas indecidibles.
Funciones con múltiples entradas y salidas
El concepto de función se puede extender a un objeto que tiene una combinación de dos (o más) valores de los argumentos a un solo resultado. Este concepto intuitivo se formaliza mediante una función cuyo dominio es el Producto cartesiano de dos o más conjuntos.
Por ejemplo, considere la multiplicación función que asocia dos números enteros a su producto: f (x, y) = x · y. Esta función se puede definir formalmente como tener dominio Z × Z, el conjunto de todos los pares de números enteros; codominio Z; y, por el gráfico, el conjunto de todos los pares ((x, y), x · y). Tenga en cuenta que el primer componente de dicho par es en sí misma un par (de números enteros), mientras que el segundo componente es un solo número entero.
El valor de la función del par (x, y) es ƒ ((x, y)). Sin embargo, es habitual para dejar un conjunto de paréntesis, y considerar ƒ (x, y) una función de dos variables (o con dos argumentos), X e Y.
El concepto puede extenderse aún más considerando una función que también produce una salida que se expresa como varias variables. Por ejemplo considerar la función de espejo (x, y) = (y, x) con el dominio R × R y codomain R × R también. El par (y, x) es un valor único en el codomain visto como un producto cartesiano.
Operaciones binarias
Lo familiar operaciones binarias de aritmética , además y multiplicación , se pueden ver como funciones de R × R a R. Este punto de vista es generalizada en álgebra abstracta , donde se utilizan las funciones n -ario para modelar el funcionamiento de las estructuras algebraicas arbitrarias. Por ejemplo, un resumen grupo se define como un conjunto X y una función f de X × X a X que satisface ciertas propiedades.
Tradicionalmente, la suma y la multiplicación están escritos en el notación infija: x + y y x × y en lugar de + (x, y) y x (x, y).
Espacios de funciones
El conjunto de todas las funciones de un conjunto X a un conjunto Y se denota por X → Y, por [X → Y], o por Y X. La última anotación se justifica por el hecho de que | Y X | = | Y | | X | y es un ejemplo de la convención de combinatoria enumerativa que proporciona notaciones para juegos basados en sus cardinalidades.
Ver el artículo sobre los números cardinales para más detalles.
Podemos interpretar ƒ: X → Y para significar ƒ ∈ [X → Y]; es decir, "ƒ es una función de X a Y".
Operaciones punto a punto
Si ƒ: X → R y g: X → R son funciones con dominio X común y codominio común un anillo R, entonces uno puede definir la función suma ƒ + g: X → R y la función del producto ⋅ ƒ g: X → R como sigue:
para todo x en X.
Esto convierte el conjunto de todas las funciones en un anillo. Las operaciones binarias en ese anillo tienen Dominio ordenó pares de funciones, y como funciones codominio. Este es un ejemplo de subir en la abstracción, a las funciones de más tipos de complejos.
Al tomar alguna otra estructura algebraica A en el lugar de la R, podemos convertir el conjunto de todas las funciones de X a A en una estructura algebraica del mismo tipo de una manera análoga.
Otras propiedades
Hay muchas otras clases especiales de funciones que son importantes para determinadas ramas de las matemáticas, o aplicaciones particulares. Aquí está una lista parcial:
- Función biyectiva. También puede visitar función inyectiva, función sobreyectiva y función biyectiva por separado.
- continuo
- diferenciable, integrable
- lineal, polinómica , racional
- algebraica, trascendental
- trigonométrico
- fractal
- par o impar
- convexa, monótona, unimodal
- holomorfa, meromórfica, todo
- vector-valorada
- calculable