
Teorema fundamental del cálculo
Antecedentes
Esta selección Escuelas fue originalmente elegido por SOS para las escuelas en el mundo en desarrollo que no tienen acceso a Internet. Está disponible como una descarga intranet. SOS Children trabaja en 45 países africanos; puede ayudar a un niño en África ?
El teorema fundamental del cálculo especifica la relación entre las dos operaciones centrales de cálculo , la diferenciación y la integración .
La primera parte del teorema, a veces llamado el primer teorema fundamental del cálculo, muestra que un integración indefinida puede ser revertida por una diferenciación.
La segunda parte, a veces llamado el segundo teorema fundamental del cálculo, le permite a uno computar la integral definida de una función mediante el uso de alguno de sus infinitos primitivas. Esta parte del teorema tiene aplicaciones prácticas inestimables, ya que simplifica notablemente el cálculo de integrales definidas.
La primera declaración publicada y prueba de una versión restringida del teorema fundamental era por James Gregory (1638-1675). Isaac Barrow probó la primera versión completamente general del teorema, mientras que los estudiantes de Barrow Isaac Newton (1643-1727) completó el desarrollo de la teoría matemática de los alrededores. Gottfried Leibniz (1646-1716) sistematiza el conocimiento en un cálculo de cantidades infinitesimales.
Intuición
Intuitivamente, el teorema simplemente establece que la suma de cambios infinitesimales en una cantidad en el tiempo (o alguna otra cantidad) suman el cambio neto en la cantidad.
Para comprender esta afirmación, vamos a empezar con un ejemplo. Supongamos que una partícula se desplaza en línea recta con la posición dada por x (t), donde t es el tiempo y x (t) significa que x es una función de t. La derivada de esta función es igual al cambio infinitesimal en cantidad, d x, por cambio infinitesimal en el tiempo, d t (por supuesto, el propio derivado depende del tiempo). Vamos a definir este cambio en la distancia, por el cambio en el tiempo como la velocidad v de la partícula. En Notación de Leibniz:
Reordenando esta ecuación, se deduce que:
Por la lógica anterior, un cambio en x (  ) Es la suma de las variaciones infinitesimales d x. También es igual a la suma de los productos infinitesimales de la derivada y el tiempo. Esta suma infinita es la integración; Por lo tanto, la operación de integración permite la recuperación de la función original de su derivado. Como se puede inferir razonablemente, esta operación funciona a la inversa como podemos diferenciar el resultado de nuestro integral para recuperar la derivada original.
) Es la suma de las variaciones infinitesimales d x. También es igual a la suma de los productos infinitesimales de la derivada y el tiempo. Esta suma infinita es la integración; Por lo tanto, la operación de integración permite la recuperación de la función original de su derivado. Como se puede inferir razonablemente, esta operación funciona a la inversa como podemos diferenciar el resultado de nuestro integral para recuperar la derivada original.
Declaraciones formales
Hay dos partes en el teorema fundamental del cálculo. Sin apretar palabras, las primera parte trata de la derivada de una primitiva, mientras que la segunda parte se ocupa de la relación entre primitivas y integrales definidas .
Primera parte
Esta parte se refiere a veces como Primer Teorema Fundamental del Cálculo.
Sea f una función real continua definida en un intervalo cerrado [a, b]. Sea F la función definida, para todo x de [a, b], por
Entonces, F es diferenciable en [a, b], y para cada x en [a, b],
 .
.
La operación  es una integral definida con límite superior variable y su resultado F (x) es uno de los infinitos primitivas de f.
es una integral definida con límite superior variable y su resultado F (x) es uno de los infinitos primitivas de f.
Segunda parte
Esta parte se refiere a veces como segundo teorema fundamental del cálculo.
Sea f una función real continua definida en un intervalo cerrado [a, b]. Sea F un primitiva de f, que es uno de los infinitamente muchas funciones tal que, para todo x de [a, b],
 .
.
Entonces
 .
.
Corolario
Sea f una función real definida en un intervalo cerrado [a, b]. Sea F una función tal que, para todo x de [a, b],
Entonces, para todo x de [a, b],
y
 .
.
Ejemplos
A modo de ejemplo, supongamos que usted necesita para calcular
Aquí,  y podemos usar
y podemos usar  como la primitiva. Por lo tanto:
como la primitiva. Por lo tanto:
O, en términos más generales, supongamos que usted necesita para calcular
Aquí,  y podemos usar
y podemos usar  como la primitiva. Por lo tanto:
como la primitiva. Por lo tanto:
Pero este resultado se podría haber encontrado mucho más fácilmente como
Prueba
Suponer que
Que haya dos números x 1 y x 1 + Δ x en [a, b]. Así que tenemos
y
Restando las dos ecuaciones da
Se puede demostrar que

- (La suma de las áreas de dos regiones adyacentes es igual al área de ambas regiones combinadas.)
La manipulación de esta ecuación da
Sustituyendo lo anterior en (1) da como resultado
De acuerdo con la significa teorema del valor para la integración, existe una c en [x 1, x 1 + Δ x] tal que
 .
.
Sustituyendo lo anterior en (2) obtenemos
 .
.
Dividiendo ambos lados por Δ x da

- Observe que la expresión en el lado izquierdo de la ecuación es la de Newton cociente de diferencias para F en x 1.
Tome el límite Δ x → 0 en ambos lados de la ecuación.
La expresión en el lado izquierdo de la ecuación es la definición de la derivada de f en x 1.
Para encontrar el otro límite, vamos a utilizar el exprimir teorema. El número c está en el intervalo [x 1, x 1 + Δ x], por lo que x 1 ≤ c ≤ x 1 + Δ x.
También,  y
y  .
.
Por lo tanto, de acuerdo con el teorema de compresión,
Sustituyendo en (3), obtenemos
La función f es continua en c, por lo que el límite puede ser tomada dentro de la función. Por lo tanto, obtenemos
 .
.
que completa la demostración.
(Leithold et al, 1996)
Prueba alternativa
Esta es una prueba límite Riemann resume.
Sea f continua en el intervalo [a, b], y sea F una primitiva de f. Comience con la cantidad
 .
.
Que no haya números
- x 1, ..., x n
de tal manera que
 .
.
Resulta que
 .
.
Ahora, añadimos cada F (x i) junto con su inverso aditivo, de modo que la cantidad resultante es igual:
La cantidad anterior se puede escribir como la siguiente suma:
A continuación vamos a emplear el teorema del valor medio. En pocas palabras,
Sea F continua en el intervalo cerrado [a, b] y derivable en el intervalo abierto (a, b). Entonces existe alguna c en (a, b) tal que
Resulta que
La función F es diferenciable en el intervalo [a, b]; por lo tanto, también es diferenciable y continua en cada intervalo de x i -1. Por lo tanto, según el teorema del valor medio (arriba),
Sustituyendo lo anterior en (1), obtenemos
El supuesto implica  También,
También,  se puede expresar como
se puede expresar como  de partición
de partición  .
.

Nótese que estamos describiendo el área de un rectángulo, con el ancho por la altura, y estamos agregando las áreas juntas. Cada rectángulo, en virtud de la Teorema del valor medio, describe una aproximación de la sección de la curva que se dibuja sobre. Observe también que  no necesita ser el mismo para cualquier valor de
no necesita ser el mismo para cualquier valor de  , O en otras palabras que la anchura de los rectángulos puede diferir. Lo que tenemos que hacer es aproximar la curva con
, O en otras palabras que la anchura de los rectángulos puede diferir. Lo que tenemos que hacer es aproximar la curva con  rectángulos. Ahora, como el tamaño de las particiones se hacen más pequeños y que n aumenta, lo que resulta en más particiones para cubrir el espacio, vamos a estar más cerca y más cerca de la superficie real de la curva.
rectángulos. Ahora, como el tamaño de las particiones se hacen más pequeños y que n aumenta, lo que resulta en más particiones para cubrir el espacio, vamos a estar más cerca y más cerca de la superficie real de la curva.
Al tomar el límite de la expresión como la norma de las particiones se aproxima a cero, llegamos a la Integral de Riemann. Es decir, tomamos el límite cuando la mayor de las particiones se aproxima a cero en tamaño, por lo que todas las demás particiones son más pequeñas y el número de particiones tiende a infinito.
Así, tomamos el límite en ambos lados de (2). Esto nos da
Ni F (b) ni F (a) es dependiente || Δ ||, así que el límite en el lado izquierdo sigue siendo F (b) - F (a).
La expresión en el lado derecho de la ecuación define una integral sobre f de A a B. Por lo tanto, obtenemos
que completa la demostración.
Las generalizaciones
No necesitamos asumir la continuidad de f en todo el intervalo. Parte I del teorema dice entonces: si f es cualquier integrable Lebesgue función en [a, b] y x 0 es un número en [a, b] tal que f es continua en x 0,
es diferenciable de x = x 0 con F '(x 0) = f (x 0). Nos podemos relajar las condiciones en f todavía más allá y suponer que no es más que localmente integrable. En ese caso, se puede concluir que la función F es diferenciable casi todas partes y F '(x) = f (x) en casi todas partes. Esto a veces se conoce como diferenciación teorema de Lebesgue.
Parte II del teorema es cierto para cualquier función integrable Lebesgue f que tiene una antiderivada F (no todas las funciones integrables hacen, sin embargo).
La versión del teorema de Taylor que expresa el término de error como una integral puede ser visto como una generalización del Teorema Fundamental.
Hay una versión del teorema de complejas funciones: supongamos U es un conjunto abierto en C y f: U → C es una función que tiene un F antiderivada holomorfa en U. Entonces, para cada curva γ: [a, b] → U, la curva integral se puede calcular como
El teorema fundamental se puede generalizar a curvas y superficies integrales en dimensiones superiores y en los colectores .
Uno de los estados más poderosos en esta dirección es El teorema de Stokes.












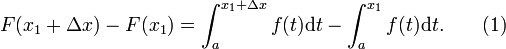






![\ Begin {matriz} F (b) - F (a) y = & F (x_n) \, + \, [- F (x_ {n-1}) \, + \, F (x_ {n-1} )] \, + \, \ ldots \, + \, [- F (x 1) + F (x 1)] \, - \, F (x 0) \, \\ & = y [F (x_n) \, - \, F (x_ {n-1})] \, + \, [F (x_ {n-1}) \, + \, \ ldots \, - \, F (x_1)] \, + \, [ F (x 1) \, - \, F (x 0)] \, \ end {matriz}](../../images/62/6206.png)
![F (b) - F (a) = \ sum_ {i = 1} ^ n [F (x_i) - F (x_ {i-1})] \ qquad (1)](../../images/62/6207.png)



![F (b) - F (a) = \ sum_ {i = 1} ^ n [F '(C_i) (x_i - x_ {i-1})].](../../images/62/6211.png)
![F (b) - F (a) = \ sum_ {i = 1} ^ n [f (C_i) (\ Delta x_i)] \ qquad (2)](../../images/62/6215.png)
![\ Lim _ {\ | \ Delta \ | \ a 0} F (b) - F (a) = \ lim _ {\ | \ Delta \ | \ a 0} \ sum_ {i = 1} ^ n [f (C_i) (\ x_i Delta)] \ ,.](../../images/62/6225.png)
![F (b) - F (a) = \ lim _ {\ | \ Delta \ | \ a 0} \ sum_ {i = 1} ^ n [f (C_i) (\ x_i Delta)]](../../images/62/6226.png)


