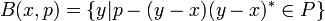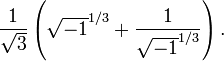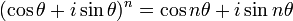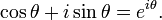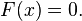Número complejo
Acerca de este escuelas selección Wikipedia
Los artículos de esta selección escuelas se han organizado por tema currículo gracias a voluntarios SOS. Todos los niños disponibles para el apadrinamiento de niños de Aldeas Infantiles SOS son atendidos en una casa de familia por la caridad. Leer más ...

En matemáticas , un número complejo es un número que se puede definir formalmente como par ordenado de números reales (a, b), a menudo escrito:
donde i 2 = -1.
Los números complejos tienen suma, resta, multiplicación y división de las operaciones definidas, con los comportamientos que son un superconjunto estricto de los números reales, así como los que tengan otras propiedades elegantes y útiles. En particular, los números reales negativos se pueden obtener elevando al cuadrado los números complejos.
Los números complejos se inventaron cuando se descubrió que la solución de algunos ecuaciones cúbicas requieren cálculos intermedios que contienen las raíces cuadradas de los números negativos, incluso cuando las soluciones finales fueron los números reales. Además, a partir de la teorema fundamental del álgebra, el uso de los números complejos como el campo número de polinomios ecuaciones algebraicas significa que siempre existen soluciones. El conjunto de números complejos formar una algebraicamente cerrado campo, en contraste con el conjunto de números reales, que no está cerrado algebraicamente.
Los números complejos se utilizan en muchos campos diferentes, incluyendo aplicaciones en la ingeniería , el electromagnetismo , la física cuántica , la matemática aplicada , y la teoría del caos . Cuando el campo subyacente de números para un tipo de matemáticas es el campo de los números complejos, el nombre suele reflejar ese hecho. Ejemplos son análisis complejo, matriz compleja , polinomio complejo y complejo álgebra de Lie.
Definiciones
Notación
Aunque otras anotaciones se pueden utilizar, los números complejos son muy a menudo escritos en forma
donde a y b son números reales , y i es la unidad imaginaria , que tiene la propiedad i 2 = -1. El número real a se llama la parte real del número complejo, y el número real b es la parte imaginaria .
Los números reales pueden expresarse como números complejos con la parte imaginaria de cero; es decir, el número real a es equivalente a la de un número complejo 0 i. Los números complejos con una parte real que es cero son llamados números imaginarios.
Por ejemplo, 3 + 2 i es un número complejo, con parte real y parte imaginaria 3 2. Si z = a + ib, la parte real (a) se denota Re (z) o 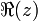 , Y la parte imaginaria (b) se denota Im (z) o
, Y la parte imaginaria (b) se denota Im (z) o 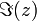 .
.
En algunas disciplinas (en particular, la ingeniería eléctrica , donde i es un símbolo para actual), la unidad imaginaria i es lugar escrito como j, por lo que los números complejos se escriben a veces como un jb +.

f (x) = (x ²-1) (x -2- i) ² /
(X ² + 2 + 2 i). El matiz representa el argumento de la función, mientras que la saturación representa la magnitud.
La conjunto de todos los números complejos se denota generalmente por C, o en pizarra audaz  . Los números reales, R, pueden considerarse como un subconjunto de C considerando todo número real como un complejo: a = a + 0 i.
. Los números reales, R, pueden considerarse como un subconjunto de C considerando todo número real como un complejo: a = a + 0 i.
Igualdad
Dos números complejos son iguales si y sólo si sus partes reales son iguales y sus partes imaginarias son iguales. Es decir, a + bi = c + di si y sólo si a = b = c y d.
Operaciones
Se agregan los números complejos, restan, multiplican y dividen aplicando formalmente la asociativa , conmutativa y leyes distributivas de la álgebra, junto con la ecuación i 2 = -1:
- Adición:

- Resta:
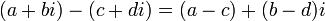
- Multiplicación:
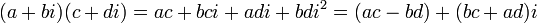
- División:

- Adición:
(División de números complejos se define más adelante).
El campo de los números complejos
Formalmente, los números complejos se pueden definir como pares ordenados de números reales (a, b), junto con las operaciones de:
Así definido, los números complejos forman un campo, el campo número complejo, denotado por C (un campo es una estructura algebraica en la que la suma, resta, multiplicación y división se definen y satisfacen ciertas leyes algebraicas. Por ejemplo, los números reales forman un campo).
El número real a se identifica con el número complejo (a, 0), y de esta manera el campo de los números reales R se convierte en un subcampo de la C. La unidad imaginaria i se puede definir como el número complejo (0, 1), que verifica
En C, tenemos:
- identidad aditiva ("cero"): (0, 0)
- identidad multiplicativa ("uno"): (1, 0)
- inverso aditivo de (a, b): (- a, - b)
- inverso multiplicativo (recíproco) de la no-cero (a, b):
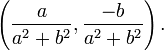
Puesto que un número complejo a + bi se especifica de forma única por un par ordenado (a, b) de los números reales, los números complejos están en uno-a-uno correspondencia con los puntos en un plano, llamado el plano complejo .
C también se puede definir como la cierre topológica de la números algebraicos o como el clausura algebraica de R, ambos de los cuales se describen a continuación.
El plano complejo

 y su conjugado
y su conjugado  en el plano complejo.
en el plano complejo. Un número complejo z puede ser visto como un punto o un vector de posición en una de dos dimensiones del sistema de coordenadas cartesianas llamado el plano complejo o diagrama de Argand (nombrado después de Jean-Robert Argand) - ver figura de la derecha. El punto y por lo tanto el número complejo z pueden ser especificados por cartesiano (rectangular) coordina. Las coordenadas cartesianas del número complejo son la parte real x = Re (z) y la parte imaginaria y = Im (z). La representación de un número complejo por sus coordenadas cartesianas se llama la forma cartesiana o en forma rectangular o forma algebraica de ese número complejo.
Valor absoluto, conjugación y la distancia
El valor absoluto (o módulo o magnitud) de un número complejo 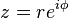 se define como
se define como 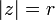 . Algebraicamente, si
. Algebraicamente, si 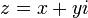 , A continuación,
, A continuación, 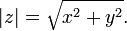
Se puede comprobar fácilmente que el valor absoluto tiene tres propiedades importantes:
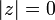 si y solo si
si y solo si 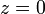
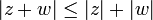 ( desigualdad triangular)
( desigualdad triangular)
para todos los números complejos z y w. De esto se deduce, por ejemplo, que 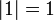 y
y  . Al definir la función de distancia
. Al definir la función de distancia 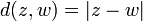 giramos el conjunto de los números complejos en un espacio métrico y por lo tanto podemos hablar de límites y continuidad.
giramos el conjunto de los números complejos en un espacio métrico y por lo tanto podemos hablar de límites y continuidad.
La complejo conjugado del número complejo 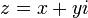 se define como
se define como  , Escrito como
, Escrito como  o
o  . Como se ve en la figura,
. Como se ve en la figura,  es el "reflejo" de z sobre el eje real. A continuación se puede comprobar:
es el "reflejo" de z sobre el eje real. A continuación se puede comprobar:
 si y sólo si z es real
si y sólo si z es real
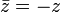 si y sólo si z es puramente imaginario
si y sólo si z es puramente imaginario
 si z no es cero.
si z no es cero.
Esta última fórmula es el método de elección para calcular la inversa de un número complejo si se administra en coordenadas rectangulares.
Que los desplazamientos de conjugación con todas las operaciones algebraicas (y muchas funciones, por ejemplo,  ) Tiene sus raíces en la ambigüedad en la elección de i (-1 tiene dos raíces cuadradas). Es importante señalar, sin embargo, que la función de
) Tiene sus raíces en la ambigüedad en la elección de i (-1 tiene dos raíces cuadradas). Es importante señalar, sin embargo, que la función de 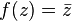 no es complejo-diferenciable (ver función holomorfa).
no es complejo-diferenciable (ver función holomorfa).
Fracciones complejas
Podemos dividir un número complejo (a + bi) por otro número complejo (c + di) ≠ 0 de dos maneras. La primera forma ya se ha implicado: para convertir los dos números complejos en forma exponencial, de la que se deriva fácilmente su cociente. La segunda forma es la de expresar la división como fracción y luego multiplicar el numerador y el denominador por el complejo conjugado del denominador. El nuevo denominador es un número real.
Interpretación geométrica de las operaciones sobre los números complejos

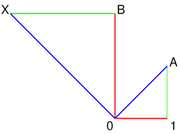

Considere la posibilidad de un avión . Un punto es el origen, 0. Otro punto es la unidad, o 1.
La suma de dos puntos A y B es el punto X = A + B de manera que los triángulos con vértices 0, A, B, y X, B, A, son congruentes.
El producto de dos puntos A y B es el punto X = AB tal que los triángulos con vértices 0, 1, A y 0, B, X, son similar.
El complejo conjugado de un punto A es el punto X = A * tal que los triángulos con vértices 0, 1, A y 0, 1, X, son imágenes especulares uno del otro.
Esta interpretación geométrica permite que los problemas de la geometría se traduzcan en álgebra. El problema de la construcción geométrica de la 17-gon este modo se tradujo en el análisis de la ecuación algebraica x 17 = 1.
Forma polar
Alternativamente a la representación cartesiana z = x + iy, el número complejo z puede ser especificado por las coordenadas polares . Las coordenadas polares son r = | z | ≥ 0, llamado el valor absoluto o módulo, y φ = arg (z), llamado el argumento o el ángulo de z. Para r = 0 cualquier valor de φ describe el mismo número. Para obtener una representación única, una elección convencional es establecer arg (0) = 0. Para r> 0 el argumento φ es único módulo 2π; es decir, si cualquiera de los dos valores de la argumento complejo difieren por una exacta número entero múltiplo de 2π, que se consideran equivalentes. Para obtener una representación única, una elección convencional es φ limitar al intervalo (-π, π], es decir, -π <φ ≤ π. La representación de un número complejo por sus coordenadas polares se llama la forma polar del número complejo .
La conversión de la forma polar a la forma cartesiana
La conversión de la forma cartesiana a la forma polar
(Ver función arg y atan2).
El valor resultante de φ está en el rango (-π, π +];. Es negativo para valores negativos de y Si los valores en lugar no negativos en el rango [0, 2π) se desean, añadir 2π a resultados negativos.
La notación de la forma polar
La notación de la forma polar como
se llama forma trigonométrica. El φ notación cis veces se utiliza como una abreviatura de cos φ + i sin φ. Uso La fórmula de Euler que también se puede escribir como
que se llama forma exponencial.
Multiplicación, división, potenciación y extracción de la raíz en forma polar
Multiplicación, división, potenciación y extracción de la raíz son mucho más fáciles en forma polar que en forma cartesiana.
Uso suma y la diferencia identidades su posible obtener que
y eso
Exponenciación con exponentes enteros; de acuerdo a Fórmula de De Moivre,
Exponenciación con exponentes complejos arbitrarios se discute en el artículo sobre la exponenciación .
La adición de dos números complejos es sólo la suma vectorial de dos vectores, y la multiplicación por un número complejo fijo puede ser visto como un giro simultáneo y estiramiento.
La multiplicación por i corresponde a una rotación hacia la izquierda por 90 grados (π / 2 radianes ). El contenido geométrico de la ecuación i 2 = -1 es que una secuencia de dos rotaciones resultados de 90 grados en un grado 180 (π radianes) de rotación. Incluso el hecho de (-1) · (-1) = 1 de la aritmética se puede entender geométricamente como la combinación de dos giros de 180 grados.
Todas las raíces de cualquier número real o complejo, se pueden encontrar con un simple algoritmo . El enésimo raíces están dadas por
para k = 0, 1, 2, ..., n - 1, donde ![\ Sqrt [n] {r}](../../images/145/14548.png) representa la principal n º raíz de r.
representa la principal n º raíz de r.
Algunas propiedades
Representación de la matriz de los números complejos
Aunque por lo general no es útil, representaciones alternativas del campo complejo pueden dar una idea de su naturaleza. Una representación particularmente elegante interpreta cada número complejo como un 2 × 2 matriz con reales entradas que se extiende y gira los puntos del plano. Cada tal matriz tiene la forma
donde a y b son números reales. La suma y el producto de dos de estas matrices es nuevo de esta forma, y el funcionamiento del producto en matrices de esta forma es conmutativa . Cada matriz no nula de este formulario es invertible y su inversa es de nuevo de esta forma. Por lo tanto, las matrices de esta forma son una campo, isomorfo al campo de los números complejos. Cada tales matriz puede ser escrito como
lo que sugiere que deberíamos identificar el verdadero número 1 con la matriz de identidad
y la unidad imaginaria i con
una rotación en sentido antihorario en 90 grados. Tenga en cuenta que el cuadrado de esta última matriz es de hecho igual a la matriz 2 × 2 que representa -1.
El cuadrado del valor absoluto de un número complejo expresado como una matriz es igual a la determinante de esa matriz.
Si la matriz es visto como una transformación del plano, entonces la transformación gira puntos a través de un ángulo igual al argumento del número complejo y escalas por un factor igual al valor absoluto del número complejo. El conjugado del número complejo z corresponde a la transformación que gira a través del mismo ángulo que z pero en la dirección opuesta, y escamas en la misma manera que z; esto puede ser representado por la transpuesta de la matriz correspondiente a z.
Si los elementos de matriz son en sí mismos números complejos, el álgebra resultante es la de la cuaterniones. En otras palabras, esta representación matricial es una forma de expresar la Cayley-Dickson construcción de álgebras.
También hay que señalar que los dos valores propios de la matriz de 2x2 que representan un número complejo son el propio número complejo y su conjugado.
Espacio vectorial real
C es un verdadero bidimensional del espacio de vector . A diferencia de los reales, el conjunto de números complejos no puede ser totalmente ordenada de cualquier manera que sea compatible con sus operaciones aritméticas: C no se puede convertir en un campo ordenado. Más en general, ningún campo que contiene una raíz cuadrada de -1 se puede pedir.
R mapas -lineal C → C tiene la forma general
con coeficientes complejos a y b. Sólo el primer término es C -lineal, y sólo el primer término es holomorfa; el segundo término es-real diferenciable, pero no satisface el Ecuaciones de Cauchy-Riemann.
La función
corresponde a rotaciones combinadas con escalamiento, mientras que la función
corresponde a las reflexiones combinadas con escalamiento.
Las soluciones de las ecuaciones polinómicas
A raíz del polinomio p es un número complejo z tal que p (z) = 0. Un resultado sorprendente en análisis complejo es que todos los polinomios de grado n con coeficientes reales o complejos tienen raíces exactamente n complejas (conteo raíces múltiples de acuerdo con su multiplicidad). Esto se conoce como la teorema fundamental del álgebra, y muestra que los números complejos son una algebraicamente cerrado.
De hecho, el complejo campo de número de C es el clausura algebraica del campo número real, y Cauchy construyó el campo de los números complejos de esta manera. También se puede caracterizar como la anillo cociente del polinomio anillo R [X] sobre la ideal generado por el polinomio X ² + 1:
Este es de hecho un campo porque X ² + 1 es irreducible, por lo tanto, la generación de una ideal máximo, en R [X]. La imagen de X en este anillo cociente es la unidad imaginaria i.
Caracterización algebraica
El campo es C ( hasta el terreno isomorfismo) caracterizado por los siguientes tres hechos:
- su característica es 0
- su grado trascendencia sobre la Primer campo es la cardinalidad del continuo
- es algebraicamente cerrado
En consecuencia, C contiene muchos subcampos adecuados que son isomorfo a C. Otra consecuencia de esta caracterización es que la Grupo de Galois de C en los números racionales es enorme, con cardinalidad igual a la del conjunto potencia del continuo.
Caracterización como un campo topológico
Como se señaló anteriormente, la caracterización algebraica de C no capta algunas de sus propiedades más importantes. Estas propiedades, que sustentan las bases de análisis complejo, surge de la topología de C. Las siguientes propiedades caracterizan C como una campo topológica:
- C es un campo.
- C contiene un subconjunto P de elementos no nulos satisfactorias:
- P está cerrado bajo la suma, multiplicación y tomando inversas.
- Si x e y son elementos distintos de P, entonces o bien xy o yx está en P
- Si S es cualquier subconjunto no vacío de P, entonces S + P = x + P para algunos x en C.
- C tiene un automorfismo involutivo no trivial x → x *, la fijación de P y de tal manera que xx * está en P para cualquier x distintos de cero en C.
Dadas estas propiedades, se puede entonces definir una topología en C mediante la adopción de los conjuntos
como un base, donde x oscila sobre C, y p se extiende sobre P.
Para ver que estas propiedades caracterizan C como una campo topológico, uno observa que P ∪ {0} ∪ -P es una ordenó Campo Dedekind-completa y por lo tanto pueden ser identificados con el número real de R por un isomorfismo campo único. La última propiedad se ve fácilmente dar a entender que la Grupo de Galois sobre los números reales es de orden dos, completando la caracterización.
Pontryagin ha demostrado que el único conectado localmente compacto campos topológicas son R y C. Esto da otra caracterización de C como un campo topológico, ya que C se puede distinguir de R señalando que los números complejos no nulos son conectado, mientras que los números reales no nulos no lo son.
Análisis complejo
El estudio de las funciones de una variable compleja se conoce como análisis complejo y tiene un enorme utilidad práctica en matemáticas aplicadas , así como en otras ramas de las matemáticas. A menudo, las pruebas más naturales para las declaraciones en análisis real o incluso la teoría de números emplean técnicas de análisis complejo (ver teorema de los números primos para un ejemplo). A diferencia de las funciones reales que están representados comúnmente como dos gráficos tridimensionales, funciones complejas tienen cuatro gráficos tridimensionales y pueden útilmente ser ilustrados por el color de codificación de una tres gráfico tridimensional para sugerir cuatro dimensiones, o por la animación de transformación dinámica del complejo de la función del plano complejo.
Aplicaciones
Las palabras "reales" y "imaginarios" tenían sentido cuando se utilizaron los números complejos, principalmente como una ayuda en la manipulación de los números "reales", con sólo la parte "real", que describe directamente el mundo. Aplicaciones posteriores, y sobre todo el descubrimiento de la mecánica cuántica, demostró que la naturaleza no tiene preferencia por los números "reales" y sus más descripciones reales a menudo requieren números complejos, la parte de "imaginario" ser tan físicos como la parte "real".
Teoría de control
En la teoría de control , los sistemas a menudo se transforman desde el dominio del tiempo a la dominio de la frecuencia usando el Transformada de Laplace. El sistema de postes y ceros se analizan entonces en el plano complejo. La lugar de las raíces, Diagrama de Nyquist, y Técnicas de trazado Nichols todos hacen uso del plano complejo.
En el método del lugar de raíces, es especialmente importante si la postes y ceros están en los planos medio izquierdo o derecho, es decir, tienen parte real mayor o menor que cero. Si un sistema tiene polos que están
- en el semiplano derecho, será inestable,
- todo en el semiplano izquierdo, será estable,
- en el eje imaginario, que tendrá estabilidad marginal.
Si un sistema tiene ceros en el semiplano derecho, es un sistema de fase no mínima.
Análisis de señales
Los números complejos se utilizan en análisis de la señal y otros campos para una descripción conveniente para las señales que varían periódicamente. Para las funciones reales dados que representan cantidades físicas reales, a menudo en términos de senos y cosenos, correspondientes funciones complejas son considerados de los cuales las partes reales son las cantidades originales. Para de onda sinusoidal de un dado la frecuencia, el valor absoluto | z | z de la correspondiente es el amplitud y el argumento arg (z) la fase.
Si Se emplea el análisis de Fourier para escribir una señal de valor real dado como una suma de funciones periódicas, estas funciones periódicas se escriben a menudo como funciones de valores complejos de la forma
donde ω representa la frecuencia angular y el número complejo z codifica la fase y la amplitud como se explicó anteriormente.
En la ingeniería eléctrica , la Transformada de Fourier se utiliza para analizar la variación voltajes y corrientes. El tratamiento de resistencias, condensadores, y inductores pueden ser unificados por la introducción de resistencias imaginarias, dependientes de la frecuencia de los dos últimos y la combinación de los tres en un solo número complejo llamado la impedancia. (Ingenieros eléctricos y algunos físicos utilizan la letra j para la unidad imaginaria desde que es típicamente reservado para diferentes corrientes y pueden entrar en conflicto con i.) Este enfoque se denomina cálculo fasorial. Este uso se extiende también en procesamiento de la señal digital y de procesamiento de imagen digital, que utilizan versiones digitales de análisis de Fourier (y Análisis Wavelet) para transmitir, comprimir, restaurar y otra cosa proceso digitales de audio señales, imágenes fijas, y señales de vídeo.
Integrales impropias
En campos aplicados, los números complejos a menudo se utilizan para calcular ciertos valores reales- integrales impropias, por medio de funciones de valores complejos. Existen varios métodos para hacer esto; ver métodos de integración de contorno.
Mecanica cuantica
El campo de número complejo es relevante en el formulación matemática de la mecánica cuántica, donde compleja Espacios de Hilbert proporcionan el contexto para una tal formulación que sea conveniente y tal vez lo más estándar. Las fórmulas fundación original de la mecánica cuántica - el Schrödinger ecuación y Heisenberg mecánica matricial - hacen uso de los números complejos.
Relatividad
En especial y la relatividad general , algunas fórmulas para la métrica de el espacio-tiempo se vuelven más simples si se toma la variable tiempo para ser imaginario. (Esto ya no es estándar.) Los números complejos son esenciales para espinores que son una generalización de la tensores utilizados en relatividad.
Matemáticas aplicadas
En las ecuaciones diferenciales , es común encontrar primero todo complejo raíces r de la ecuación característica de una ecuación diferencial lineal y luego tratar de resolver el sistema en términos de funciones de base de la forma f (t) = e rt.
Dinámica de fluidos
En dinámica de fluidos, funciones complejas se utilizan para describir flujo potencial en dos dimensiones.
Fractales
Ciertos fractales se representan en el plano complejo por ejemplo conjunto de Mandelbrot y Conjunto de Julia.
Historia
La referencia más temprana a la fugaz raíces cuadradas de números negativos quizás ocurrió en el trabajo del griego matemático e inventor Herón de Alejandría en el siglo 1 dC , cuando se considera el volumen de un imposible tronco de pirámide , aunque los números negativos no fueron concebidos en el Mundo helenístico.
Los números complejos se hicieron más prominentes en el siglo 16 , cuando se cierran las fórmulas para las raíces de cúbico y cuárticas polinomios fueron descubiertos por los matemáticos italianos (ver Niccolo Fontana Tartaglia, Gerolamo Cardano). Pronto se dio cuenta de que estas fórmulas, incluso si uno sólo estaba interesado en soluciones reales, a veces requieren la manipulación de las raíces cuadradas de números negativos. Por ejemplo, la fórmula cúbico de Tartaglia da la siguiente solución a la ecuación x ³ - x = 0:
A primera vista esto parece una tontería. Sin embargo cálculos formales con números complejos muestran que la ecuación z = 3 i ha soluciones -i,  y
y 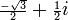 . Sustituyendo estos a su vez para
. Sustituyendo estos a su vez para 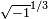 en la fórmula cúbico de Tartaglia y simplificando, se obtiene 0, 1 y -1 como las soluciones de x 3 - x = 0.
en la fórmula cúbico de Tartaglia y simplificando, se obtiene 0, 1 y -1 como las soluciones de x 3 - x = 0.
Esto fue doblemente inquietante puesto que se consideraba ni siquiera los números negativos para estar en tierra firme en el momento. El término "imaginario" para estas cantidades fue acuñado por René Descartes en 1637 y estaba destinado a ser despectivo (ver número imaginario para una discusión de la "realidad" de los números complejos). Otra fuente de confusión es que la ecuación 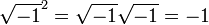 parecía ser caprichosamente incompatible con la identidad algebraica
parecía ser caprichosamente incompatible con la identidad algebraica 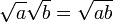 , Que es válida para los positivos números reales a y b, y que también se utilizó en cálculos con números complejos con uno de a, b positivo y el otro negativo. El uso incorrecto de esta identidad (y la identidad relacionados
, Que es válida para los positivos números reales a y b, y que también se utilizó en cálculos con números complejos con uno de a, b positivo y el otro negativo. El uso incorrecto de esta identidad (y la identidad relacionados 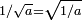 ) En el caso de que tanto a como b son negativos incluso bedeviled Euler . Esta dificultad finalmente llevó a la convención de usar el símbolo especial i en lugar de
) En el caso de que tanto a como b son negativos incluso bedeviled Euler . Esta dificultad finalmente llevó a la convención de usar el símbolo especial i en lugar de 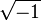 para evitar este error.
para evitar este error.
El siglo 18 vio los trabajos de Abraham de Moivre y Leonhard Euler . Para Moivre es debido (1730) la conocida fórmula que lleva su nombre, fórmula de De Moivre:
y Euler (1748) La fórmula de Euler de análisis complejo:
La existencia de los números complejos no fue completamente aceptada hasta la interpretación geométrica (ver abajo) había sido descrito por Caspar Wessel en 1799 ; fue redescubierto varios años más tarde y popularizado por Carl Friedrich Gauss , y como resultado la teoría de los números complejos recibió una notable expansión. La idea de la representación gráfica de los números complejos había aparecido, sin embargo, ya en 1685, en Tractatus de Álgebra de Wallis.
Las memorias de Wessel apareció en las Actas de la Copenhague Academia de 1799, y es sumamente clara y completa, incluso en comparación con las obras modernas. También considera la esfera, y da una teoría de cuaterniones de la que se desarrolla una trigonometría esférica completa. En 1804 el Abbé Buée llegó de manera autónoma la misma idea que Wallis había sugerido, que 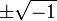 debe representar una línea de unidad, y su negativa, perpendicular al eje real. Papel de Buée no se publicó hasta 1806, año en que Jean-Robert Argand también publicó un folleto sobre el mismo tema. Es el ensayo de Argand que la base científica para la representación gráfica de los números complejos que ahora se conoce generalmente. Sin embargo, en 1831 Gauss encontró la teoría bastante desconocida, y en 1832 publicó su libro de memorias jefe sobre el tema, con lo que destacada ante el mundo matemático. Cabe mencionar también hecha de un excelente pequeño tratado por Mourey (1828), en el que las bases de la teoría de los números de dirección son científicamente establecido. La aceptación general de la teoría no es un poco debido a los trabajos de Augustin Louis Cauchy y Niels Henrik Abel, y sobre todo este último, que fue el primero en utilizar audazmente los números complejos con un éxito que es bien conocida.
debe representar una línea de unidad, y su negativa, perpendicular al eje real. Papel de Buée no se publicó hasta 1806, año en que Jean-Robert Argand también publicó un folleto sobre el mismo tema. Es el ensayo de Argand que la base científica para la representación gráfica de los números complejos que ahora se conoce generalmente. Sin embargo, en 1831 Gauss encontró la teoría bastante desconocida, y en 1832 publicó su libro de memorias jefe sobre el tema, con lo que destacada ante el mundo matemático. Cabe mencionar también hecha de un excelente pequeño tratado por Mourey (1828), en el que las bases de la teoría de los números de dirección son científicamente establecido. La aceptación general de la teoría no es un poco debido a los trabajos de Augustin Louis Cauchy y Niels Henrik Abel, y sobre todo este último, que fue el primero en utilizar audazmente los números complejos con un éxito que es bien conocida.
Los términos comunes utilizados en la teoría se deben principalmente a los fundadores. Argand llamada 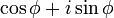 el factor de dirección, y
el factor de dirección, y 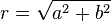 el módulo; Cauchy (1828) llama
el módulo; Cauchy (1828) llama 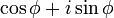 la forma reducida (l'réduite expresión); Gauss utiliza i para
la forma reducida (l'réduite expresión); Gauss utiliza i para 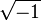 , Presentó el número complejo plazo para
, Presentó el número complejo plazo para  Y llamado
Y llamado 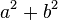 la norma.
la norma.
El coeficiente dirección expresión, a menudo utilizado para 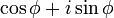 , Se debe a Hankel (1867), y el valor absoluto, para el módulo, se debe a Weierstrass.
, Se debe a Hankel (1867), y el valor absoluto, para el módulo, se debe a Weierstrass.
Después de Cauchy y Gauss han recorrido un número de contribuyentes de alto rango, de los cuales los siguientes pueden ser especialmente mencionado: Kummer (1844), Leopold Kronecker (1845), Scheffler (1845, 1851, 1880), Bellavitis (1835, 1852), Peacock (1845), y De Morgan (1849). Möbius también debe ser mencionado por sus numerosas memorias sobre las aplicaciones geométricas de los números complejos, y Dirichlet para la expansión de la teoría para incluir los números primos, congruencias, reciprocidad, etc., como en el caso de los números reales.
Un complejo anillo o campo es un conjunto de números complejos que es cerrado bajo la suma, resta y multiplicación. Gauss estudió los números complejos de la forma  , Donde a y b son integral, o racional (y i es una de las dos raíces de
, Donde a y b son integral, o racional (y i es una de las dos raíces de 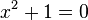 ). Su alumno, Ferdinand Eisenstein, estudió el tipo
). Su alumno, Ferdinand Eisenstein, estudió el tipo 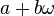 , Donde
, Donde  es una raíz compleja de
es una raíz compleja de 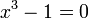 . Otros dichas clases (llamados campos ciclotómicos) de números complejos se derivan de la raíces de la unidad
. Otros dichas clases (llamados campos ciclotómicos) de números complejos se derivan de la raíces de la unidad 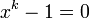 para los valores más altos de
para los valores más altos de  . Esta generalización se debe principalmente a Kummer, quien también inventó números ideales, que se expresaron como entidades geométricas por Felix Klein en 1893. La teoría general de campos fue creado por Evariste Galois, que estudió los campos generados por las raíces de cualquier ecuación polinómica
. Esta generalización se debe principalmente a Kummer, quien también inventó números ideales, que se expresaron como entidades geométricas por Felix Klein en 1893. La teoría general de campos fue creado por Evariste Galois, que estudió los campos generados por las raíces de cualquier ecuación polinómica
Los escritores tardíos (de 1884) sobre la teoría general incluyen Weierstrass, Schwarz, Richard Dedekind, Otto Hölder, Bonaventure Berloty, Henri Poincaré, Eduard Estudio, y Alexander MacFarlane.
La definición formalmente correcta utilizando pares de números reales se dio en el siglo 19 .
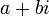
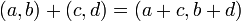
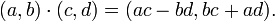
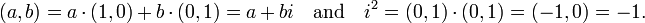

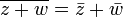
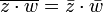
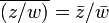
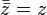
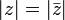

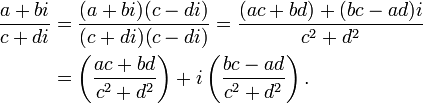
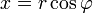
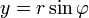
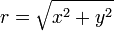
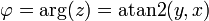

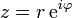


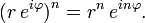
![\ Sqrt [n] {re ^ {i \ varphi}} = \ sqrt [n] {r} \ e ^ {i \ left (\ frac {\ varphi + 2k \ pi} {n} \ right)}](../../images/145/14547.png)

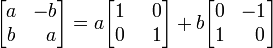
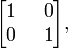
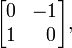
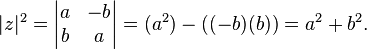
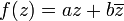
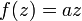
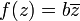
![\ Mathbb {C} = \ mathbb {R} [X] / (X ^ 2 + 1). \,](../../images/145/14557.png)