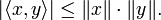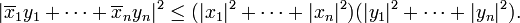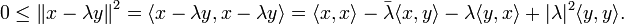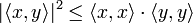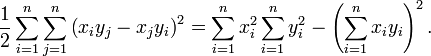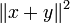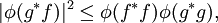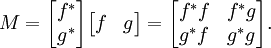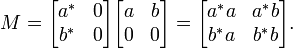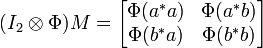Desigualdad de Cauchy-Schwarz

Temas relacionados: Matemáticas

Antecedentes de las escuelas de Wikipedia

Esta selección wikipedia ha sido elegido por los voluntarios que ayudan Infantil SOS de Wikipedia para esta Selección Wikipedia para las escuelas. Una buena manera de ayudar a otros niños es mediante el patrocinio de un niño

En matemáticas , la desigualdad de Cauchy-Schwarz, también conocida como la desigualdad de Schwarz, la desigualdad de Cauchy, o la desigualdad de Cauchy-Bunyakovsky-Schwarz, es una desigualdad útil encontrado en muchos entornos diferentes, tales como álgebra lineal aplicado a los vectores , en el análisis aplicado a serie infinita y la integración de los productos, y en teoría de la probabilidad , aplicados a las varianzas y covarianzas.

La desigualdad por sumas fue publicado por Augustin Cauchy (1821), mientras que la desigualdad correspondiente para las integrales se afirmó por primera Viktor Yakovlevich Bunyakovsky (1859) y redescubierto por Hermann Amandus Schwarz (1888) (a menudo mal escrito "Schwartz").

Declaración de la desigualdad

La desigualdad de Cauchy-Schwarz establece que para todos los vectores x e y de un verdadero o complejo espacio con producto interno,

$| \ Langle x, y \ rangle | ^ 2 \ leq \ langle x, x \ rangle \ cdot \ langle y, y \ rangle,$

donde $\ Langle \ cdot, \ cdot \ rangle$ es el producto interno. De manera equivalente, tomando la raíz cuadrada de ambos lados, y en referencia a la normas de los vectores, la desigualdad se escribe como

$| \ Langle x, y \ rangle | \ leq \ | x \ | \ cdot \ | y \ |. \,$

Además, los dos lados son iguales si y sólo si $x$ y $y$ son linealmente dependiente (o, en un sentido geométrico, son paralelo o uno de los vectores es igual a cero).

Si $x_1, \ cdots, x_n \ in \ mathbb C$ y $y_1, \ cdots, y_n \ in \ mathbb C$ son los componentes de $x$ y $y$ con respecto a una ortonormal base de $V$ la desigualdad puede ser reexpresada de una manera más explícita como sigue:

$| \ Overline {x} _1 y_1 + \ cdots + \ overline {x} _n y_n | ^ 2 \ leq (| x 1 | ^ 2 + \ cdots + | x_n | ^ 2) (| y_1 | ^ 2 + \ cdots + | y_n | ^ 2).$

Igualdad si y sólo si, ya sea $x = 0$ O existe un escalar $\ Lambda$ de tal manera que

$y_1 = \ lambda x_1, \ y_2 = \ lambda x_2, \ dots, y_n = \ lambda x_n.$

El caso de dimensión finita de esta desigualdad para los vectores reales fue probado por Cauchy en 1821, y en 1859 los estudiantes de Cauchy V.Ya. Bunyakovsky señaló que mediante la adopción de límites se puede obtener una forma integral de la desigualdad de Cauchy. El resultado general de un espacio con producto interno se obtuvo KHASchwarz en 1885.

Prueba

A medida que la desigualdad es trivialmente cierto en el caso y = 0, podemos suponer <y, y> es distinto de cero. Dejar $\ Lambda$ ser un número complejo . Luego,

$0 \ leq \ left \ | x \ lambda y \ right \ | ^ 2 = \ langle x \ lambda y, x- \ lambda y \ rangle = \ langle x, x \ rangle - \ bar {\ lambda} \ langle x, y \ rangle - \ lambda \ langle y, x \ rangle + | \ lambda | ^ 2 \ langle y, y \ rangle.$

Elección

$\ Lambda = \ langle x, y \ rangle \ cdot \ langle y, y \ rangle ^ {- 1}$

obtenemos

$0 \ leq \ langle x, x \ rangle - | \ langle x, y \ rangle | ^ 2 \ cdot \ langle y, y \ rangle ^ {- 1}$

cual es verdad si y solo si

$| \ Langle x, y \ rangle | ^ 2 \ leq \ langle x, x \ rangle \ cdot \ langle y, y \ rangle$

o equivalentemente:

que es la desigualdad de Cauchy-Schwarz.

Casos especiales notables

R ⁿ

En espacio euclidiano R ⁿ con el producto interior estándar, la desigualdad de Cauchy-Schwarz es

$\ Left (\ sum_ {i = 1} ^ n x_i y_i \ right) ^ 2 \ leq \ left (\ sum_ {i = 1} ^ n x_i ^ 2 \ right) \ left (\ sum_ {i = 1} ^ n y_i ^ 2 \ right).$

En este caso especial, una prueba alternativa es la siguiente: Considere el polinomio en z

$(X_1 z + y_1) ^ 2 + \ cdots + (x_n z + y_n) ^ 2.$

Tenga en cuenta que el polinomio es cuadrática en z. Desde el polinomio es no negativo, no puede tener ninguna raíz a menos que todas las velocidades x _i / y _i son iguales. De ahí su discriminante es menor que o igual a cero, es decir,

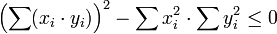$\ Left (\ sum (x_i \ cdot y_i) \ right) ^ 2 - \ sum {x_i ^ 2} \ cdot \ sum {y_i ^ 2} \ le 0$ ,

que produce la desigualdad de Cauchy-Schwarz.

Una prueba equivalente a la I ⁿ comienza con el sumatorio siguiente.

La ampliación de los soportes que tenemos:

$\ Sum_ {i = 1} ^ n \ sum_ {j = 1} ^ n \ left (x_i y_j - x_j y_i \ right) ^ 2 = \ sum_ {i = 1} ^ n x_i ^ 2 \ sum_ {j = 1 } ^ n y_j ^ 2 + \ sum_ {j = 1} ^ n x_j ^ 2 \ sum_ {i = 1} ^ n y_i ^ 2 - 2 \ sum_ {i = 1} ^ n x_i y_i \ sum_ {j = 1 } ^ n x_j y_j$ ,

recogida de términos idénticos juntos (aunque con diferentes índices de sumatoria) encontramos:

$\ Frac {1} {2} \ sum_ {i = 1} ^ n \ sum_ {j = 1} ^ n \ left (x_i y_j - x_j y_i \ right) ^ 2 = \ sum_ {i = 1} ^ n x_i ^ 2 \ sum_ {i = 1} ^ n y_i ^ 2 - \ left (\ sum_ {i = 1} ^ n x_i y_i \ right) ^ 2.$

Debido a que el lado izquierdo de la ecuación es una suma de los cuadrados de los números reales es mayor que o igual a cero, por lo tanto:

$\ Sum_ {i = 1} ^ n x_i ^ 2 \ sum_ {i = 1} ^ n y_i ^ 2 - \ left (\ sum_ {i = 1} ^ n x_i y_i \ right) ^ 2 \ geq 0$ .

Además, cuando n = 2 o 3, el producto escalar se relaciona con el ángulo entre dos vectores y uno puede ver inmediatamente la desigualdad:

$| X \ cdot y | = \ | x \ | \ | y \ | | \ cos \ theta | \ le \ | x \ | \ | y \ |.$

Además, en este caso la desigualdad de Cauchy-Schwarz puede también deducirse a partir de Identidad de Lagrange. Para n = 3, la identidad de Lagrange toma la forma

$\ Langle x, x \ rangle \ cdot \ langle y, y \ rangle = | \ langle x, y \ rangle | ^ 2 + | x \ épocas y | ^ 2$

de la que sigue fácilmente la desigualdad de Cauchy-Schwarz.

L ²

Para el espacio de producto interno de valores complejos cuadrados integrables funciones , uno tiene

$\ Left | \ int f (x) \ overline {g} (x) \, dx \ right | ^ 2 \ leq \ int \ left | f (x) \ right | ^ 2 \, dx \ cdot \ int \ dejó | g (x) \ right | ^ 2 \, dx.$

Una generalización de esto es el La desigualdad de Hölder.

Uso

La desigualdad triangular para el producto interior se muestra a menudo como consecuencia de la desigualdad de Cauchy-Schwarz, como sigue: dado vectores x e y,

$\ \| X + y \ \| ^ 2$	$= \ Langle x + y, x + y \ rangle$
	$= \ \| X \ \| ^ 2 + \ langle x, y \ rangle + \ langle y, x \ rangle + \ \| y \ \| ^ 2$
	$\ Le \ \| x \ \| ^ 2 + 2 \| \ langle x, y \ rangle \| + \ \| y \ \| ^ 2$
	$\ Le \ \| x \ \| ^ 2 + 2 \ \| x \ \| \ \| y \ \| + \ \| y \ \| ^ 2$
	$\ Le \ left (\ \| x \ \| + \ \| y \ \| \ right) ^ 2$

Tomando las raíces cuadradas da la desigualdad triangular.

La desigualdad de Cauchy-Schwarz permite extender la noción de "ángulo entre dos vectores" para cualquier verdadero espacio con producto interno, mediante la definición de:

$\ Cos \ theta_ {xy} = \ frac {\ langle x, y \ rangle} {\ | x \ | \ | y \ |}$

La desigualdad de Cauchy-Schwarz prueba que esta definición es sensible, al demostrar que el lado derecho se encuentra en el intervalo $[-1,1]$ , Y justifica la idea de que los espacios interiores de productos reales son simplemente generalizaciones del espacio euclidiano.

El Cauchy-Schwarz se utiliza para demostrar que el producto interior es una función continua con respecto a la topología inducida por el producto interno en sí.

La desigualdad de Cauchy-Schwarz se utiliza generalmente para mostrar La desigualdad de Bessel.

La formulación general de la Principio de incertidumbre de Heisenberg se obtiene utilizando la desigualdad de Cauchy-Schwarz en el espacio de producto interno de física funciones de onda.

Las generalizaciones

Existen varias generalizaciones de la desigualdad de Cauchy-Schwarz en el contexto de teoría de operadores, por ejemplo para las funciones de operador-convexa, y álgebra de operadores, donde el dominio y / o el rango de φ se sustituyen por una C * álgebra o W -algebra *.

Esta sección enumera algunas de esas desigualdades respecto al ajuste álgebra de operadores, para dar una idea de los resultados de este tipo.

Funcionales positivos en C * - y W -álgebras *

Uno puede discutir productos internos como los funcionales positivos. Dado un espacio de Hilbert L ² (m), siendo M una medida finita, el producto interno <·, ·> da lugar a una funcional positiva φ por

$\ Phi (g) = \ langle g, 1 \ rangle.$

Desde <f, f> ≥ 0, φ (f f *) ≥ 0 para todo f en L ² (m), donde f * es puntual conjugado de f. Entonces φ es positivo. Por el contrario cada φ funcional positivo da un producto interno correspondiente <f, g> _φ = φ (g * f). En este lenguaje, la desigualdad de Cauchy-Schwarz se convierte

$| \ Phi (g ^ * f) | ^ 2 \ leq \ phi (f ^ * f) \ phi (g ^ * g),$

que se extiende al pie de la letra los funcionales positivos en C * álgebras.

Ahora nos damos una prueba teórica operador de la desigualdad de Cauchy-Schwarz, que pasa a la configuración C * álgebra. Uno puede ver a partir de la prueba de que la desigualdad de Cauchy-Schwarz es una consecuencia de la positividad y anti-simetría axiomas-producto interno.

Considere la matriz positiva

$M = \ begin {bmatrix} f ^ * ^ * g \\ \ end {bmatrix} \ begin {bmatrix} f & g \ end {bmatrix} = \ begin {bmatrix} f ^ * f & f ^ * g \\ g ^ * f & g ^ * g \ end {bmatrix}.$

Desde φ es un mapa lineal positiva cuyo rango, los números complejos C, es un conmutativa C * álgebra, φ es totalmente positivo. Por lo tanto

$M '= (I_2 \ otimes \ phi) (M) = \ begin {bmatrix} \ phi (f ^ * f) y \ phi (f ^ * g) \\ \ phi (g ^ * f) y \ phi ( g ^ * g) \ end {bmatrix}$

es una matriz escalar de 2 × 2 positivo, lo que implica que tiene determinante positivo:

$\ Phi (f ^ * f) \ phi (g ^ * g) - | \ phi (g ^ * f) | ^ 2 \ geq 0 \ quad \ mbox {es decir,} \ quad \ phi (f ^ * f) \ phi (g ^ * g) \ geq | \ phi (g ^ * f) | ^ 2.$

Esta es precisamente la desigualdad de Cauchy-Schwarz. Si fyg son elementos de un C * álgebra, F * y g * denotar sus respectivos adjoints.

También podemos deducir desde arriba que cada funcional lineal positiva está limitada, lo que corresponde al hecho de que el producto interior es de forma conjunta continua.

Mapas positivos

Funcionales positivos son casos especiales de mapas positivos. Un Φ mapa lineal entre C * álgebras se dice que es un mapa positivo si a ≥ 0 implica Φ (a) ≥ 0. Es natural preguntarse si existen desigualdades de tipo Schwarz para mapas positivos. En este contexto más general, se necesitan suposiciones generalmente adicionales para obtener dichos resultados.

La desigualdad de Kadison

Una de estas desigualdades es la siguiente:

Teorema Si Φ es un mapa positivo unital, a continuación, para cada elemento normal de una en su dominio, que tiene Φ (a * a) ≥ Φ (a *) Φ (a) y Φ (a * a) ≥ Φ (a) Φ (a *).

Esto extiende el hecho de φ (a * a) · 1 ≥ φ (a) * φ (a) = | φ (a) | ^2, cuando φ es una funcional lineal.

El caso cuando a es autoadjunto, es decir, a = a *, que se conoce como la desigualdad de Kadison.

Mapas 2-positivos

Cuando Φ es 2-positivo, una hipótesis más fuerte que meramente positivo, uno tiene algo que se ve muy similar a la original, la desigualdad de Cauchy-Schwarz:

Teorema (Modificado desigualdad de Schwarz para los mapas 2-positivas) Para un mapa Φ 2-positiva entre C * álgebras, para todo a, b en su dominio,

i) Φ (a) * Φ (a) ≤ || Φ (1) || Φ (a * a).

ii) || Φ (a * b) || ² ≤ || Φ (a * a) || · || Φ (b * b) ||.

Un argumento simple para ii) es como sigue. Considere la matriz positiva

$M = \ begin {bmatrix} a ^ * y 0 \\ b ^ * y 0 \ end {bmatrix} \ begin {bmatrix} a & b \\ 0 & 0 \ end {bmatrix} = \ begin {bmatrix} a ^ * A & A ^ * b \\ b ^ * a & b ^ * b \ end {bmatrix}.$

Por 2-positividad de Φ,

$(I_2 \ otimes \ Phi) M = \ begin {bmatrix} \ Phi (a ^ * a) y \ Phi (a ^ * b) \\ \ Phi (b ^ * a) y \ Phi (b ^ * b) \ end {bmatrix}$

es positivo. La desigualdad deseada y luego se sigue de las propiedades de 2 × 2 (operador) matrices positivas.

I Parte) es análoga. Se puede reemplazar la matriz $\ Begin {bmatrix} a & b \\ 0 & 0 \ end {bmatrix}$ por $\ Begin {bmatrix} 1 y un \\ 0 & 0 \ end {bmatrix}.$

Recuperado de " http://en.wikipedia.org/w/index.php?title=Cauchy-Schwarz_inequality&oldid=199248245 "

$\ \| X + y \ \| ^ 2$	$= \ Langle x + y, x + y \ rangle$
	$= \ \| X \ \| ^ 2 + \ langle x, y \ rangle + \ langle y, x \ rangle + \ \| y \ \| ^ 2$
	$\ Le \ \| x \ \| ^ 2 + 2 \| \ langle x, y \ rangle \| + \ \| y \ \| ^ 2$
	$\ Le \ \| x \ \| ^ 2 + 2 \ \| x \ \| \ \| y \ \| + \ \| y \ \| ^ 2$
	$\ Le \ left (\ \| x \ \| + \ \| y \ \| \ right) ^ 2$

See also ebooksgratis.com: no banners, no cookies, totally FREE.