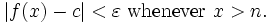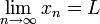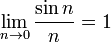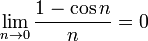Límite (matemáticas)

Temas relacionados: Matemáticas

Sabías ...

La organización de una selección de Wikipedia para escuelas en el mundo en desarrollo sin internet fue una iniciativa de SOS Children. Apadrina un niño para hacer una diferencia real.

El wikilibro Cálculo tiene una página sobre el tema de: Límites

En matemáticas , el concepto de un "límite" se utiliza para describir la comportamiento de una función como su argumento o bien "se acerca" a un cierto punto, o como se hace arbitrariamente grande; o el comportamiento de una secuencia de elementos 's como su índice aumenta indefinidamente. Los límites se utilizan en el cálculo y otras ramas de análisis matemático para definir derivados y continuidad.

El concepto de "límite de una función" es más generalizado al concepto de red topológica, mientras que el límite de una secuencia está estrechamente relacionada con límite y límite directo en la teoría de categorías.

Límite de una función

Supongamos ƒ (x) es una Función real y c es un número real . La expresión:

$\ Lim_ {x \ to c} f (x) = L$

significa que ƒ (x) se pueden hacer para estar tan cerca de L como se desee haciendo x suficientemente cerca c. En ese caso, se dice que "el límite de f de x, cuando x tiende a c, es L". Tenga en cuenta que esta declaración puede ser cierto incluso si 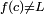$\ Scriptstyle f (c) \ neq L$ . De hecho, la función f (x) tiene por qué ni siquiera se define en c. Dos ejemplos ayudan a ilustrar esto.

Considerar 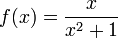$f (x) = \ frac {x} {x ^ 2 + 1}$ cuando x tiende a 2. En este caso, f (x) se define a las 2 y es igual a su límite de 0,4:

f (1,9)	f (1.99)	f (1.999)	f (2)	f (2.001)	f (2.01)	f (2,1)
0.4121	0.4012	0.4001	$\ Flecha Correcta$ 0.4 $\ Flecha Izquierda$	0.3998	0.3988	0.3882

Cuando x se aproxima 2, f (x) se acerca a 0,4 y por lo tanto tenemos $\ Scriptstyle \ lim_ {x \ 2} f (x) = 0,4$ . En el caso donde $\ Scriptstyle f (c) = \ {lim_ x \ to c} f (x)$ Ƒ se dice que es continua en x = c. Pero no siempre es el caso. Considerar

$g (x) = \ left \ {\ begin {matriz} \ frac {x} {x ^ 2 + 1}, y \ mbox {si} x \ ne 2 \\ \\ 0, & \ mbox {si} x = 2. \ End {matriz} \ right.$

El límite de g (x) cuando x tiende a 2 es 0,4 (igual que en ƒ (x)), pero $\ Scriptstyle \ lim_ {x \ 2} g (x) \ neq g (2)$ ; G no es continua en x = 2.

O piense en el caso en que f (x) no está definida en x = c.

$f (x) = \ frac {x - 1} {\ sqrt {x} - 1}$

En este caso, cuando x tiende a 1, f (x) no está definida en x = 1, pero el límite es igual a 2:

f (0,9)	f (0.99)	f (0.999)	f (1,0)	f (1.001)	f (1.01)	f (1,1)
1.95	1.99	1,999	$\ Flecha Correcta$ undef $\ Flecha Izquierda$	2,001	2,010	2.10

Por lo tanto, f (x) puede hacerse arbitrariamente cerca del límite de 2 con sólo hacer x suficientemente cerca de 1.

Definición formal

Karl Weierstrass define formalmente un límite de la siguiente manera:

Sea f una función definida en un intervalo abierto que contiene c (excepto posiblemente en c) y dejar L un número real .

$\ Lim_ {x \ to c} f (x) = L$

significa que

para cada verdadero ε> 0 existe un verdadero δ> 0 tal que para todo x con 0 <| x - c | <δ, tenemos | f (x) - L | <ε.

La definición formal de un límite a veces se llama la forma delta-epsilon, ya que utiliza las letras griegas delta (δ) y epsilon (ε). El uso de las letras griegas particulares δ y ε es más tradicional; la definición, por supuesto, ser sin cambios si se utilizaron diferentes letras o símbolos.

Precaución: Debe tenerse en cuenta que esta definición proporciona una forma de reconocer un límite sin proporcionar una manera de calcularlo. A menudo se necesita encontrar un límite utilizando métodos informales, especialmente cuando f (x) es discontinua en c, por ejemplo, cuando f es una relación con un denominador que es 0 en c. Hay que comprobar que el resultado realmente cumple con la definición de Weierstrass en tales casos.

Límite de una función en el infinito

Un concepto relacionado a los límites cuando x tiende a un número finito es el límite cuando x tiende a positivo o negativo infinito . Esto no significa literalmente significa que la diferencia entre x e infinito se hace pequeño, ya que el infinito no es un número real; Más bien, significa que o bien x crece sin unido positivamente (infinito positivo) o crece sin unido negativamente (infinito negativo).

Por ejemplo, considere f (x) = 2 x / (x + 1).

f (100) = 1,9802
f (1.000) = 1,9980
f (10000) = 1,9998

Como x se convierte en extremadamente grande, el valor de f (x) se aproxima a 2, y el valor de f (x) se puede hacer como cerca de 2 como uno podría desear simplemente escogiendo x suficientemente grande. En este caso, se dice que el límite de f (x) cuando x tiende a infinito es 2. En notación matemática,

$\ Lim_ {x \ to \ infty} f (x) = 2.$

Formalmente, tenemos la definición

$\ Lim_ {x \ to \ infty} f (x) = c$ si y sólo si para cada ε> 0 existe un n tal que

$| F (x) - c | <\ varepsilon \ text {} cuando x> n.$

Tenga en cuenta que la n en la definición generalmente dependerá ε. Una definición similar se aplica para $\ Scriptstyle \ lim_ {x \ a - \ infty} f (x) = c.$

Si se considera la dominio de f sea el línea número real extendida, entonces el límite de una función en el infinito puede ser considerado como un caso especial de límite de una función en un punto.

Límite de una secuencia

Considere la siguiente secuencia: 1.79, 1.799, 1.7999, ... pudimos observar que los números están "acercando" 1.8, el límite de la sucesión.

Formalmente, supongamos que x _1, x _2, ... es una secuencia de números reales . Nosotros decimos que el número real L es el límite de esta secuencia y escribimos

$\ Lim_ {n \ to \ infty x_n} = L$

si y sólo si para cada número real ε> 0 existe un número natural n ₀ (que dependerá de ε) tal que para todo n> ₀ tenemos n | x _n - L | <ε.

Intuitivamente, esto significa que con el tiempo todos los elementos de la secuencia de acercarse lo que queremos hasta el límite, ya que el valor absoluto | x _n - L | es la distancia entre x _n y L. No todos secuencia tiene un límite; si lo hace, lo llamamos convergente, divergente de lo contrario. Se puede demostrar que una secuencia convergente sólo tiene un límite.

El límite de una secuencia y el límite de una función están estrechamente relacionados. Por un lado, el límite de una secuencia es simplemente el límite en el infinito de una función definida en números naturales . Por otro lado, un límite de una función f en x, si es que existe, es el mismo que el límite de la secuencia x _n = f (x + 1 / n).

Identidades útiles

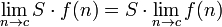$\ Lim_ {n \ a c} S \ SDOT f (n) = S \ DTS \ lim_ {n \ ac} f (n)$ , Donde S es una multiplicador escalar.
$\ N \ lim_ {ac} b ^ {f (n)} = b ^ {\ lim_ {n \ ac} f (n)}$ , Donde b es una constante.

Las siguientes reglas son válidas sólo si los límites en el lado derecho existe y son finitos.

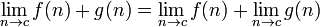
$\ Lim_ {n \ para c} f (n) + g (n) = \ lim_ {n \ para c} f (n) + \ lim_ {n \ para c} g (n)$
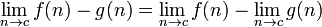
$\ Lim_ {n \ para c} f (n) - g (n) = \ lim_ {n \ para c} f (n) - \ lim_ {n \ para c} g (n)$
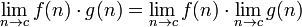
$\ Lim_ {n \ para c} f (n) \ SDOT g (n) = \ lim_ {n \ para c} f (n) \ DTS \ lim_ {n \ para c} g (n)$
$\ Lim_ {n \ a c} \ frac {f (n)} {g (n)} = \ frac {\ lim_ {n \ ac} f (n)} {\ lim_ {n \ ac} g ( n)}$ , Si el denominador contiene el límite no es igual a cero

Si cualquiera de los límites en el lado derecho es indefinido o infinito, las reglas no funcionan necesariamente.

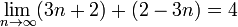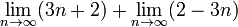Por ejemplo, $\ Lim_ {n \ to \ infty} (3n + 2) + (2-3n) = 4$ pero $\ Lim_ {n \ to \ infty} (3n + 2) + \ lim_ {n \ to \ infty} (2-3n)$ es indefinido.

Límites de interés adicional

$\ Lim_ {n \ a 0} \ frac {\ sin n} {n} = 1$
$\ Lim_ {n \ a 0} \ frac {1 - \ eos n} {n} = 0$
$\ Lim_ {n \ to \ infty} \ frac {\ sin n} {n} = 0$
$\ Lim_ {n \ to \ infty} \ frac {\ cos n} {n} = 0$

la regla de l'Hôpital

Utiliza esta regla derivados y tiene un uso condicional. Sólo se puede utilizar en formas indeterminadas.

$\ Lim_ {n \ a c} \ frac {f (n)} {g (n)} = \ lim_ {n \ a c} \ frac {f '(n)} {g' (n)}$

Por ejemplo: $\ Lim_ {n \ a 0} \ frac {\ sin (2n)} {\ sin (3n)} = \ lim_ {n \ a 0} \ frac {2 \ cos (2n)} {3 \ cos (3n) } = \ frac {2 \ SDOT 1} {3 \ SDOT 1} = \ frac {2} {3}$

Sumatorias

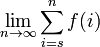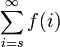
Un camino corto a escribir el límite $\ Lim_ {n \ to \ infty} \ sum_ {i = s} ^ {n} f (i)$ es $\ Sum_ {i = s} ^ {\ infty} f (i)$

Red topológica

Todas las nociones anteriores de límite se pueden unificar y generalizar arbitrariamente espacios topológicos introduciendo topológico redes y la definición de sus límites. El artículo sobre redes elabora sobre esto.

Una alternativa es el concepto de límite para filtros en espacios topológicos.

Límite en la teoría de categorías

Recuperado de " http://en.wikipedia.org/w/index.php?title=Limit_(mathematics)&oldid=189022086 "

See also ebooksgratis.com: no banners, no cookies, totally FREE.