Sustracción

"5 - 2 = 3" (verbalmente, "cinco menos dos es igual a tres")

Un problema de ejemplo

En aritmética , resta es uno de los cuatro básica operaciones binarias; es la inversa de la adición , lo que significa que si comenzamos con cualquier número y agregar cualquier número y luego restamos el mismo número que agregamos, volvemos al número que empezamos. La resta se denota por una menos sesión notación infija, en contraste con el uso del signo más para la adición.

Desde la resta no es conmutativa operador, los dos operandos son nombrados. Los nombres tradicionales para las partes de la fórmula

c - b = a

se minuendo (c) - sustraendo (b) = diferencia (a).

La resta se utiliza para modelar cuatro procesos relacionados:

1. De una colección determinada, llevar (restar) un número determinado de objetos. Por ejemplo, 5 manzanas menos 2 manzanas hojas 3 manzanas.
2. A partir de una medición dada, quitan una cantidad medida en las mismas unidades. Si yo peso 200 libras, y perder 10 libras, entonces yo peso 200-10 = 190 libras.
3. Comparar dos cantidades como para encontrar la diferencia entre ellos. Por ejemplo, la diferencia entre los $ 800 y $ 600 es $ 800 - $ 600 = $ 200. También conocida como la resta comparativa.
4. Para encontrar la distancia entre dos puntos a una distancia fija desde el punto de partida. Por ejemplo, si, en una carretera determinada, verá un marcador de kilometraje que dice 150 millas y más tarde aparece un marcador de kilometraje que dice 160 millas, que han viajado 160-150 = 10 millas.

En matemáticas , a menudo es útil para ver o incluso definir la resta como una especie de Además , la adición de la inverso aditivo. Podemos ver 7-3 = 4 como la suma de dos términos: 7 y -3. Esta perspectiva nos permite aplicar a la resta todas las reglas familiares y la nomenclatura de adición. La resta no es asociativa o conmutativa -de hecho, es anticonmutativo y asociativo por la izquierda, pero la adición de números con signo es a la vez.

Resta básica: enteros

Imagine un segmento de línea de longitud b con el extremo izquierdo marcado como y el extremo derecho etiquetada c. A partir de una, se tarda b pasos a la derecha para llegar a c. Este movimiento hacia la derecha se modela matemáticamente por adición :

a + b = c.

Desde c, se tarda b pasos a la izquierda para volver a una. Este movimiento a la izquierda se modela por sustracción:

c - b = a.

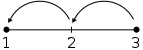
Ahora, un segmento de línea etiquetados con los números 1 , 2, y 3. A partir de la posición 3, no tiene pasos a la izquierda para permanecer en el 3, por lo que el 3 - 0 = 3. Toma 2 pasos a la izquierda para llegar a la posición 1, así que 3 - 2 = 1. Esta foto es inadecuada para describir lo que sucedería después de pasar 3 pasos a la izquierda de la posición 3. Representar a tal operación, la línea debe ser extendido.

Para restar arbitrarias números naturales , uno comienza con una línea que contiene cada número natural (0, 1, 2, 3, 4, 5, 6, ...). De 3, se tarda 3 pasos a la izquierda para llegar a 0, por lo que 3 - 3 = 0. Pero 3-4 sigue siendo válida, ya que de nuevo sale de la línea. Los números naturales no son un contexto útil para la resta.

La solución es considerar el número entero línea de números (..., -3, -2, -1, 0, 1, 2, 3, ...). De 3, toma 4 pasos a la izquierda para llegar a -1:

3 - 4 = -1.

Resta como la adición

Hay algunos casos en los que la resta como una separada la operación se vuelve problemática. Por ejemplo, 3 - (-2) (es decir, restar -2 de 3) no es inmediatamente obvio ya sea de un número natural vista o una vista de línea de números, porque no es claro lo que significa mover -2 pasos a la izquierda o tomar distancia -2 manzanas. Una solución es ver resta como la suma de números con signo. Signos menos extra simplemente denotan inversión de aditivo. Entonces tenemos 3 - (-2) = 3 + 2 = 5. Esto también ayuda a mantener el anillo de los enteros "simple", evitando la introducción de "nuevos" operadores como la resta. Ordinariamente un anillo sólo tiene dos operaciones definidas en el mismo; en el caso de los números enteros, éstos son la suma y la multiplicación. Un anillo ya tiene el concepto de inversos aditivos, pero no tiene ninguna noción de una operación de resta separado, por lo que el uso de la adición firmado como la resta nos permite aplicar los axiomas de anillo a la resta sin necesidad de demostrar nada.

Algoritmos para la resta

Hay varios algoritmos para la resta, y que difieren en su idoneidad para diversas aplicaciones. Una serie de métodos se adaptan a cálculo manual ; por ejemplo, al hacer el cambio, no se realiza la resta real, sino más bien el cambio de decisiones sigue subiendo.

Para el cálculo de la máquina, la es el método preferido de complementos, por lo que la resta se sustituye por una adición en una aritmética modular.

La enseñanza de la resta en las escuelas

Los métodos utilizados para enseñar la resta para escuela primaria varía de país a país, y dentro de un país, los diferentes métodos están de moda en diferentes momentos. En lo que se, en la Estados Unidos , llamado matemáticas tradicionales, un proceso específico se enseña a los estudiantes al final del 1er año o durante el segundo año para su uso con números enteros de varios dígitos, y se extiende ya sea en el cuarto o quinto grado para incluir representaciones decimales de los números fraccionarios.

Algunas escuelas estadounidenses actualmente enseñan un método de sustracción utilizando el endeudamiento y un sistema de marcas denominado muletas. Aunque un método de endeudamiento había sido conocido y publicado en los libros de texto antes, al parecer las muletas son la invención de William A. Brownell quien los utilizó en un estudio en noviembre de 1937. Este sistema prendió rápidamente, desplazando a los otros métodos de sustracción en uso en América en ese momento.

Algunas escuelas europeas emplean un método de sustracción llama el método austriaco, también conocido como el método de adiciones. No hay endeudamiento en este método. También hay muletas (marcas para ayudar a la memoria), que varían según el país.

Ambos métodos se rompen la resta como un proceso de restas de un dígito por el valor de posición. A partir de un dígito menos significativo, una resta de sustraendo:

s _j s _{j -1} ... s ₁

de minuendo

m _{k k -1} m ... m _1,

donde cada _i y m s _i es un dígito, procede por escribir m ₁ - s _1, m ₂ - s _2, y así sucesivamente, siempre que s _i no supera m _i. De lo contrario, m _i se incrementa en un 10 y algún otro dígito es modificado para corregir este aumento. El método estadounidense corrige por intentar disminuir el dígito minuendo m _{i +1} por uno (o continuar el préstamo hacia la izquierda hasta que no es un dígito distinto de cero desde la que prestar). El método europeo corrige mediante el aumento de la cifra sustraendo s _{i +1} por uno.

Ejemplo: 704 - 512. El minuendo es 704, el sustraendo es 512. Los dígitos minuendo son m ₃ = 7, m ₂ = 0 ym = ₁ 4. Los dígitos sustraendo son s ₃ = 5, s ₂ = 1 y s ₁ = 2. Comenzando en lugar de las unidades, 4 no es menos del 2 por lo que la diferencia 2 se anota en un solo lugar del resultado. En el lugar de los diez, 0 es menor que 1, por lo que el 0 se incrementa a 10, y la diferencia con 1, que es 9, se escribe en lugar de los diez. El método estadounidense corrige para el aumento de diez reduciendo el dígito en cientos lugar del minuendo por uno. Es decir, el 7 está tachado y sustituido por un 6. La sustracción procede entonces en el lugar de las centenas, donde 6 es no inferior a 5, lo que la diferencia se escribe en lugar del resultado de cien. Ahora hemos terminado, el resultado es de 192.

El método austriaco no reduce el 7 a 6. Más bien aumenta el sustraendo cien dígitos por uno. Una pequeña marca se hace cerca o por debajo de esta cifra (dependiendo de la escuela). A continuación, los resta procede por preguntar qué número cuando aumentó un 1, y 5 se añade a la misma, hace 7. La respuesta es 1, y se anota en el lugar del resultado de cien.

Hay una sutileza adicional en que el estudiante siempre emplea una tabla resta mental en el método americano. El método austriaco menudo anima al alumno a utilizar mentalmente la tabla de sumar a la inversa. En el ejemplo anterior, en lugar de la adición de 1 a 5, consiguiendo 6, y restando de que a partir del 7, el estudiante se le pide que considerar qué número, cuando aumentó un 1, 5 y se añade a la misma, hace 7.

Unidad

Al restar dos números con unidades, deben tener la misma unidad. En la mayoría de casos, la diferencia tendrá la misma unidad que los números originales. Una excepción es cuando la resta de dos números con porcentaje como unidad. En este caso, la diferencia tendrá puntos porcentuales como unidad.