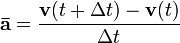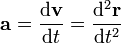Aceleración
Antecedentes
Esta selección Wikipedia está disponible sin conexión de SOS Children para su distribución en el mundo en desarrollo. Con Infantil SOS se puede elegir a apadrinar a los niños en más de cien países
"Acelerar redirecciones aquí. Ver Acelerar (desambiguación). Para el álbum de REM, consulte Acelerar (álbum de REM)

En la física , la aceleración se define como la tasa de cambio de velocidad , o como la segunda derivada de la posición (con respecto al tiempo). Es entonces un vector de la cantidad con la dimensión longitud / tiempo ². En Unidades del SI, la aceleración se mide en metros / segundo² (m · s -2). El término "aceleración" generalmente se refiere al cambio en la velocidad instantánea.
En lenguaje común, la aceleración término sólo se utiliza para un aumento de la velocidad; una disminución en la velocidad de desaceleración se llama. En la física, cualquier aumento o disminución de la velocidad se conoce como la aceleración y de manera similar, el movimiento en un círculo a velocidad constante es también una aceleración, ya que el componente dirección de la velocidad está cambiando. Ver también las leyes del movimiento de Newton .
Relación con la relatividad
Después de completar su teoría de la relatividad especial , Albert Einstein se dio cuenta de que las fuerzas de sentidos por los objetos sometidos a constante aceleración apropiada son indistinguibles de los de un campo gravitatorio. Esta fue la base para su desarrollo de la relatividad general , una teoría relativista de la gravedad . Esta es también la base para el popular Paradoja de los gemelos, que se pregunta por qué se envejece gemelas menos cuando se aleja de su hermano a casi la velocidad de la luz y luego regresar, ya que el gemelo que no envejece puede decir que es el otro gemelo que se movía. La relatividad general resolvió el "¿Por qué sólo un objeto sentirse acelerado? " problema que tenía filósofos plagadas y científicos desde los tiempos de Newton (Newton y causó endosar espacio absoluto). En la relatividad especial, sólo marcos de referencia inerciales (tramas no acelerado) se pueden utilizar y son equivalentes; relatividad general considera todos los marcos, incluso aceleradas, sean equivalentes. (El camino de estas consideraciones a la teoría completa de la relatividad general se traza en la Introducción a la relatividad general .)
Fórmula
La fórmula para la aceleración media durante un período de tiempo  es
es
donde
 es la velocidad final
es la velocidad final  es la velocidad inicial
es la velocidad inicial 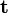 es el tiempo inicial y
es el tiempo inicial y 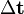 es el cambio en el tiempo
es el cambio en el tiempo
La fórmula para la aceleración instantánea en el momento  es
es
Por lo tanto la aceleración es la primera derivada de la velocidad. Hay que señalar que la expresión (posición final - Posición inicial) / (tiempo de corte) es la velocidad media y el límite como el intervalo de tiempo tiende a cero es la velocidad instantánea. Por lo tanto, la velocidad es la primera derivada de la posición, por lo que la aceleración de la segunda.
También hay que destacar que la media y aceleraciones instantáneas durante un período de tiempo 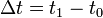 se relacionan a través de la Teorema del valor medio para integrales:
se relacionan a través de la Teorema del valor medio para integrales:
Poniendo todo junto medios:
donde
 es la aceleración
es la aceleración  es la velocidad
es la velocidad  es la posición
es la posición 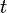 es tiempo
es tiempo