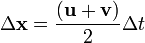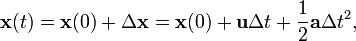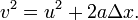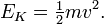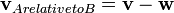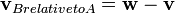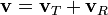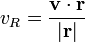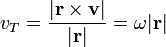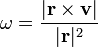Contenido Checked

Velocidad

Temas relacionados: Matemáticas

Antecedentes de las escuelas de Wikipedia

Organizar una selección Wikipedia para las escuelas en el mundo en desarrollo sin acceso a Internet era una iniciativa de SOS Children. Con Infantil SOS se puede elegir a apadrinar a los niños en más de cien países

En la física , la velocidad se define como la tasa de cambio de posición. Es un vector cantidad física; tanto la velocidad y el sentido de definirlo. En el SI sistema (métrico), que se mide en metros por segundo: (m / s) o ms -1. La escalar valor absoluto ( magnitud) de la velocidad es velocidad. Por ejemplo, "5 metros por segundo" es un escalar y no un vector, mientras que los "5 metros por segundo este" es un vector. La velocidad v media de un objeto en movimiento a través de un desplazamiento 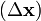(\ Delta \ mathbf {x}) durante un intervalo de tiempo (\ Delta t) se describe por la fórmula:

\ Bar {\ mathbf {v}} = \ frac {\ Delta \ mathbf {x}} {\ Delta t}

La velocidad de cambio de la velocidad se conoce como la aceleración .

Ecuación del movimiento

En el instante en el vector velocidad v de un objeto que tiene posiciones de x (t) en el tiempo t y x (t + 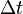{\ Delta t} ) En el tiempo t + 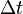{\ Delta t} , Se puede calcular como la derivada de la posición:

\ Mathbf {v} = \ lim _ {\ Delta t \ a 0} {{\ mathbf {x} (t + \ Delta t) - \ mathbf {x} (t)} \ sobre \ Delta t} = {\ mathrm { d} \ mathbf {x} \ sobre \ mathrm {d} t}

La ecuación para la velocidad de un objeto puede obtenerse matemáticamente mediante la adopción de la integral de la ecuación para su comienzo aceleración de algún tiempo inicial período t_0 hasta cierto punto en el tiempo más tarde t_n .

La velocidad final v de un objeto que se inicia con velocidad u y luego se acelera a una aceleración constante durante un período de tiempo (\ Delta t) es:

\ Mathbf {v} = \ vec {u} + \ mathbf {a} \ Delta t

La velocidad media de un objeto sometido a constante de aceleración es 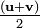\ Begin {matriz} \ frac {(\ mathbf {u} + \ mathbf {v})} {2} \; \ End {matriz} , Donde u es la velocidad inicial y v es la velocidad final. Para encontrar el desplazamiento, x, de tal objeto acelerar durante un intervalo de tiempo, \ Delta t , Entonces:

\ Delta \ mathbf {x} = \ frac {(\ mathbf {u} + \ mathbf {v})} {2} \ Delta t

Cuando sólo se conoce la velocidad inicial del objeto, la expresión,

\ Delta \ mathbf {x} = \ vec {u} \ Delta t + \ frac {1} {2} \ mathbf {a} \ t Delta ^ 2,

puede ser usado.

Esto se puede ampliar para dar la posición en cualquier tiempo t de la siguiente manera:

\ Mathbf {x} (t) = \ mathbf {x} (0) + \ Delta \ mathbf {x} = \ mathbf {x} (0) + \ mathbf {u} \ Delta t + \ frac {1} { 2} \ mathbf {a} \ t Delta ^ 2,

Estas ecuaciones básicas para la velocidad final y el desplazamiento se pueden combinar para formar una ecuación que es independiente del tiempo, también conocido como Ecuación de Torricelli:

v ^ 2 = u ^ 2 + 2a \ Delta x. \,

Las ecuaciones anteriores son válidas tanto para la mecánica de Newton y la relatividad especial . Cuando la mecánica newtoniana y la relatividad especial difieren es en la forma en que diferentes observadores describirían la misma situación. En particular, en la mecánica newtoniana, todos los observadores están de acuerdo en el valor de t y las reglas de transformación para la posición de crear una situación en la que todos los observadores que no acelera describirían la aceleración de un objeto con los mismos valores. Tampoco es cierto para la relatividad especial. En otras palabras, sólo velocidad relativa se puede calcular.

En la mecánica de Newton, la energía cinética ( energía de movimiento), 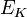E_ {K} , De un objeto en movimiento es lineal tanto con su masa y el cuadrado de su velocidad:

E_ {K} = \ begin {matriz} \ frac {1} {2} \ end {matriz} mv ^ 2.

La energía cinética es una cantidad escalar.

La velocidad de escape es la velocidad mínima de un cuerpo debe tener para poder escapar del campo gravitatorio de la Tierra. Para escapar del campo gravitatorio de la Tierra un objeto debe tener una mayor energía cinética que su energía potencial gravitatoria. El valor de la velocidad de escape de la Tierra es de aproximadamente 11.100 m / s

Velocidad relativa

La velocidad relativa es una medida de la velocidad entre dos objetos como determinado en un solo sistema de coordenadas. La velocidad relativa es fundamental tanto en la física clásica y moderna, ya que muchos sistemas de acuerdo con la física del movimiento relativo de dos o más partículas. En la mecánica de Newton, la velocidad relativa es independiente del sistema de referencia inercial elegido. Este no es el caso más con la relatividad especial en el que las velocidades dependen de la elección del sistema de referencia.

Si un objeto A se mueve con velocidad vector v y un objeto B con vector de velocidad w, entonces la velocidad del objeto A con relación al objeto B se define como la diferencia de los dos vectores de velocidad:


\ Mathbf {v} _ {Arelative Tob} = \ mathbf {v} - \ mathbf {w}

Del mismo modo la velocidad relativa del objeto B se mueve con velocidad w, relativa al objeto A se mueve con velocidad v es:


\ Mathbf {v} _ {Brelative Toa} = \ vec {w} - \ mathbf {v}

Por lo general, el marco inercial se elige en el que el último de los dos objetos mencionados está en reposo.

Velocidades escalares

En el caso unidimensional, las velocidades son escalares y la ecuación es o bien:


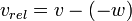v_ {rel} = v - (w) , Si los dos objetos se mueven en direcciones opuestas, o:

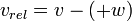v_ {rel} = v - (+ w) , Si los dos objetos se mueven en la misma dirección.

Coordenadas polares

En coordenadas polares , una velocidad de dos dimensiones se describe por una velocidad radial, definida como la componente de la velocidad lejos de o hacia el origen (también conocida como velocidad hizo bueno), y una velocidad angular , que es la tasa de rotación alrededor del origen (con cantidades positivas que representan la rotación en sentido antihorario y cantidades negativas representan giro a la derecha, en un sistema de coordenadas de mano derecha).

El radial y velocidades angulares se pueden derivar de los vectores de velocidad y de desplazamiento cartesianos descomponiendo el vector de velocidad en componentes radiales y transversales. La velocidad transversal es la componente de la velocidad a lo largo de un círculo centrado en el origen.

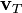\ Mathbf {v} = \ mathbf {v} _T + \ mathbf {v} _R

donde

\ Mathbf {v} _T es la velocidad transversal
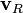\ Mathbf {v} _R es la velocidad radial

La magnitud de la velocidad radial es el producto escalar del vector de velocidad y el vector unitario en la dirección del desplazamiento.

v_R = \ frac {\ mathbf {v} \ cdot \ mathbf {r}} {\ left | \ mathbf {r} \ right |}

donde

\ Mathbf {r} es el desplazamiento

La magnitud de la velocidad transversal es el de el producto cruzado del vector unitario en la dirección del desplazamiento y el vector de velocidad. También es el producto de la velocidad angular ( \ Omega ) Y la magnitud del desplazamiento.

v_T = \ frac {| \ mathbf {r} \ times \ mathbf {v} |} {| \ mathbf {r} |} = \ omega | \ mathbf {r} |

de tal manera que

\ Omega = \ frac {| \ mathbf {r} \ times \ mathbf {v} |} {| \ mathbf {r} | ^ 2}


El momento angular en forma escalar es la masa por la distancia a los tiempos de origen la velocidad transversal, o equivalentemente, la masa por la distancia veces al cuadrado de la velocidad angular. La convención de signos para el momento angular es la misma que para la velocidad angular.

L = mrv_T = mr ^ 2 \ omega \,

donde

m \, es la masa
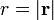
r = | \ mathbf {r} |

Si las fuerzas son en la dirección radial sólo con una dependencia de la inversa del cuadrado, como en el caso de un gravitacional órbita, el momento angular es constante, y la velocidad transversal es inversamente proporcional a la distancia, la velocidad angular es inversamente proporcional a la distancia al cuadrado, y la velocidad a la que el área se barre a cabo es constante. Estas relaciones son conocidas como leyes de Kepler del movimiento planetario

Recuperado de " http://en.wikipedia.org/w/index.php?title=Velocity&oldid=207711794 "