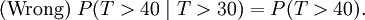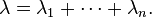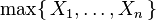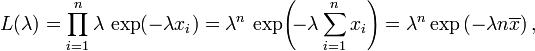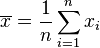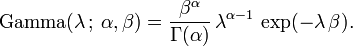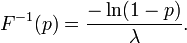Distribución exponencial

Temas relacionados: Matemáticas

Antecedentes de las escuelas de Wikipedia

SOS Children, una organización benéfica educación , organizó esta selección. Con Infantil SOS se puede elegir a apadrinar a los niños en más de cien países

Exponencial
La función de densidad de probabilidad
Función de distribución acumulativa
Parámetros	$\ Lambda> 0 \,$ tasa o escala inversa ( verdadero )
Apoyo	$[0, \ infty) \!$
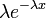PDF	$\ Lambda e ^ {- \ lambda x}$
CDF	$1 - e ^ {- \ lambda x}$
Significar	$\ Frac {1} {\ lambda} \,$
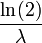Mediana	$\ Frac {\ (2) ln} {\ lambda} \,$
Modo	$0 \,$
Desacuerdo	$\ Lambda ^ {- 2} \,$
Oblicuidad	$2 \,$
Ex. curtosis	$6 \,$
Entropía	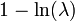$1 - \ ln (\ lambda) \,$
MGF	$\ Left (1 - \ frac {t} {\ lambda} \ right) ^ {- 1} \,$
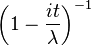CF	$\ Left (1 - \ frac {que} {\ lambda} \ right) ^ {- 1} \,$

En teoría de la probabilidad y la estadística , las distribuciones exponenciales son una clase de continuas distribuciones de probabilidad . Una distribución exponencial surge naturalmente cuando se modela el tiempo entre eventos independientes que suceden a una velocidad media constante.

Caracterización

La función de densidad de probabilidad

La función de densidad de probabilidad (pdf) de una distribución exponencial tiene la forma

$f (x; \ lambda) = \ left \ {\ begin {matriz} \ lambda e ^ {- \ lambda x} y, \; x \ ge 0, \\ 0 &, \; x <0. \ end {matriz} \ right.$

donde λ> 0 es un parámetro de la distribución, a menudo llamado el parámetro de velocidad. La distribución se apoya en el intervalo [0, ∞). Si una variable aleatoria X tiene esta distribución, escribimos X ~ Exponencial (λ).

Función de distribución acumulativa

La función de distribución acumulada está dada por

$F (x; \ lambda) = \ left \ {\ begin {matriz} 1-e ^ {- \ lambda x} y, \; x \ ge 0, \\ 0 &, \; x <0. \ end {matriz} \ right.$

Parametrización alternativo

Una parametrización alternativa comúnmente utilizado es definir la función de densidad de probabilidad (pdf) de una distribución exponencial como

$f (x; \ beta) = \ left \ {\ begin {matriz} \ frac {1} {\ beta} e ^ {- x / \ beta} y, \; x \ ge 0, \\ 0 &, \; x <0. \ end {matriz} \ right.$

donde β> 0 es un parámetro de escala de la distribución y es la recíproco de la tasa parámetro, λ, se ha definido anteriormente. En esta especificación, β es un parámetro de la supervivencia en el sentido de que si una variable aleatoria X es la duración de tiempo que un sistema biológico o mecánico dado M arregla para sobrevivir y X ~ Exponencial (β), entonces $\ Mathbb {E} [X] = \ beta$ . Es decir, la duración prevista de la supervivencia de M es β unidades de tiempo.

Esta especificación alternativa a veces es más conveniente que la dada anteriormente, y algunos autores lo utilizará como una definición estándar. No asumiremos esta especificación alternativa. Desafortunadamente esto da lugar a una ambigüedad de notación. En general, el lector debe comprobar cuál de estas dos especificaciones se utiliza si un autor escribe "X ~ Exponencial (λ)", ya que o bien la notación en el anterior (usando λ) o la notación en esta sección (aquí, utilizando β para evitar la confusión) podría ser prevista.

Ocurrencia y aplicaciones

La distribución exponencial se produce naturalmente cuando se describen las longitudes de los tiempos entre llegadas en un homogénea Procesos de Poisson.

La distribución exponencial puede ser visto como una contraparte continua de la distribución geométrica, que describe el número de Ensayos de Bernoulli necesarias para un proceso discreto cambien de estado. En contraste, la distribución exponencial describe el tiempo para un proceso continuo de cambio de estado.

En los escenarios del mundo real, el supuesto de una tasa constante (o probabilidad por unidad de tiempo) es rara vez satisfecho. Por ejemplo, la tasa de llamadas telefónicas entrantes difiere de acuerdo con la hora del día. Pero si nos centramos en un intervalo de tiempo durante el cual la tasa es más o menos constante, por ejemplo, de 2 a 4 pm durante los días de trabajo, la distribución exponencial se puede utilizar como un buen modelo aproximado para el tiempo hasta la siguiente llamada telefónica llega. Advertencias similares se aplican a los siguientes ejemplos que producen variables de aproximadamente distribuidos de manera exponencial:

el tiempo hasta que una partícula radiactiva decae, o el tiempo entre pitidos de una contador Geiger;
el tiempo que toma antes de su próxima llamada telefónica
el tiempo hasta que por defecto (en el pago a los tenedores de deuda de la compañía) en forma reducida de modelos de riesgo de crédito

Las variables exponenciales también se pueden utilizar para modelar situaciones donde se producen ciertos eventos con una probabilidad constante por unidad de distancia:

la distancia entre mutaciones en un ADN hebra;
la distancia entre roadkill en una calle determinada;

En la teoría de colas, los tiempos entre llegadas (es decir, los tiempos entre los clientes que entran en el sistema) a menudo se modelan como variables distribuidas de manera exponencial. La longitud de un proceso que puede ser pensado como una secuencia de varias tareas independientes es mejor modelada por una variable después de la Distribución Erlang (que es la distribución de la suma de varias variables distribuidas exponencialmente independientes).

La fiabilidad y la teoría ingeniería de confiabilidad también hacen un amplio uso de la distribución exponencial. Debido a la sin memoria característica de esta distribución, es muy adecuado para modelar la constante porción tasa de riesgo de la curva de la bañera utilizada en la teoría fiabilidad. También es muy conveniente, ya que es tan fácil de añadir las tasas de fracaso de un modelo de fiabilidad. Sin embargo, la distribución exponencial no es apropiado para modelar el curso de la vida en general de los organismos o dispositivos técnicos, porque las "tasas de fracaso" aquí no son constantes: más fracasos ocurren por muy jóvenes y para los sistemas muy antiguos.

En la física , si observa un gas a una determinada temperatura y presión en un uniforme campo gravitatorio, las alturas de las diversas moléculas también siguen una distribución exponencial aproximada. Esto es una consecuencia de la propiedad entropía se menciona a continuación.

Propiedades

Media y varianza

La media o valor esperado de una variable aleatoria distribuida exponencialmente X con parámetro de tasa λ es dado por

$\ Mathrm {E} [X] = \ frac {1} {\ lambda}. \!$

A la luz de los ejemplos dados anteriormente, esto tiene sentido: si recibe llamadas de teléfono a una tasa promedio de 2 por hora, entonces usted puede esperar que esperar media hora para cada llamada.

La varianza de X está dada por

$\ Mathrm {} Var [X] = \ frac {1} {\ lambda ^ 2}. \!$

Memorylessness

Una propiedad importante de la distribución exponencial es que es sin memoria. Esto significa que si al azar una variable T se distribuye de manera exponencial, su obedece probabilidad condicional

$P (T> s + t \; | \; t> s) = P (T> t) \; \; \ Hbox {for all} \ s, t \ ge 0.$

Esto dice que la probabilidad condicional de que tenemos que esperar, por ejemplo, más de otros 10 segundos antes de la primera llegada, dado que la primera llegada aún no ha sucedido después de 30 segundos, no es diferente de la probabilidad inicial que tenemos que esperar más de 10 segundos por primera llegada. Esto es a menudo mal entendida por los estudiantes que toman cursos en la probabilidad: el hecho de que P (T> 40 | T> 30) = P (T> 10) no quiere decir que los eventos T> 40 y T> 30 son independiente. Para resumir: "memorylessness" de la distribución de probabilidad del tiempo de espera T hasta que los primeros medios de llegada

$\ Mathrm {(Derecho)} \ P (T> 40 \ mediados T> 30) = P (T> 10).$

Esto no significa

$\ Mathrm {(incorrecto)} \ P (T> 40 \ mediados T> 30) = P (T> 40).$

(Eso sería la independencia. Estos dos eventos no son independientes.)

Las distribuciones exponenciales y la distribuciones geométricas son las únicas distribuciones de probabilidad sin memoria.

La distribución exponencial también tiene una constante función de riesgo.

Los cuartiles

La función cuantil (función de distribución acumulada inversa) para Exponencial (λ) es

$F ^ {- 1} (p; \ lambda) = \ frac {- \ ln (1-p)} {\ lambda}, \!$

para 0 ≤ p <1. El cuartiles son, por tanto:

primer cuartil: $\ Ln (4/3) / \ lambda \,$
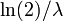
mediana: $\ Ln (2) / \ lambda \,$
tercer cuartil: $\ Ln (4) / \ lambda \,$

Kullback-Leibler

El dirigida Kullback-Leibler divergencia entre Exp (λ ₀₎ ("verdadero" distribución) y Exp (λ) ('aproximar' distribución) está dada por

$\ Delta (\ lambda || \ lambda_0) = \ log (\ lambda) - \ log (\ lambda_0) + \ frac {\ lambda_0} {\ lambda} - 1.$

Distribución máxima entropía

Entre todas las distribuciones de probabilidad continuas con el apoyo [0, ∞) y μ decir, la distribución exponencial con λ = 1 / μ tiene la más grande entropía.

Distribución del mínimo de variables aleatorias exponenciales

Sea X _1, ..., X _n ser variables aleatorias distribuidas exponencialmente independientes con parámetros de velocidad de λ _1, ..., λ _n. Entonces

$\ Min \ {\, x_1, \ dots, X_n \, \}$

También tiene una distribución exponencial, con el parámetro

$\ Lambda = \ lambda_1 + \ cdots + \ lambda_n. \,$

Sin embargo,

$\ Max \ {\, x_1, \ dots, X_n \, \}$

no se distribuye de manera exponencial.

La estimación de parámetros

Supongamos que usted sabe que una determinada variable se distribuye de forma exponencial y se desea estimar el parámetro de tasa λ.

Máxima verosimilitud

La función de verosimilitud para λ, da un muestra independiente e idénticamente distribuidos x = (x _1, ..., x _n) a partir de la variable, es

$L (\ lambda) = \ prod_ {i = 1} ^ n \ lambda \, \ exp (- \ lambda x_i) = \ lambda ^ n \, \ exp \ \ left (\ -! \ Lambda \ sum_ {i = 1} ^ n x_i \ right) = \ lambda ^ n \ exp \ left (- \ lambda n \ overline {x} \ right),$

donde

$\ Overline {x} = {1 \ over n} \ sum_ {i = 1} ^ n x_i$

es la media de la muestra.

La derivada de logaritmo de la función de verosimilitud es

$\ Frac {\ mathrm {d}} {\ mathrm {d} \ lambda} \ ln L (\ lambda) = \ frac {\ mathrm {d}} {\ mathrm {d} \ lambda} \ left (n \ ln (\ lambda) - \ lambda n \ overline {x} \ right) = {n \ sobre \ lambda} -n \ overline {x} \ \ left \ {\ begin {matriz}> 0 & \ mbox {si} \ 0 <\ lambda <1 / \ overline {x}, \\ \\ = 0 & \ mbox {si} \ \ lambda = 1 / \ overline {x}, \\ \\ <0 y \ mbox {si} \ \ lambda> 1 / \ overline {x}. \ End {matriz} \ right.$

En consecuencia, la estimación de máxima verosimilitud para el parámetro de velocidad es

$\ Widehat {\ lambda} = \ frac1 {\ overline {x}}.$

Inferencia bayesiana

La conjugado previa para la distribución exponencial es la distribución gamma (de los cuales la distribución exponencial es un caso especial). La siguiente parametrización del pdf gamma es útil:

$\ Mathrm {Gamma} (\ lambda \,; \, \ alpha, \ beta) = \ frac {\ beta ^ {\ alpha}} {\ Gamma (\ alpha)} \, \ lambda ^ {\ alpha-1} \, \ exp (- \ lambda \, \ beta). \!$

La distribución a posteriori p puede entonces ser expresada en términos de la función de probabilidad definido anteriormente y un gamma antes:

$P (\ lambda) \ propto L (\ lambda) \ times \ mathrm {Gamma} (\ lambda \,; \, \ alpha, \ beta)$

$= \ Lambda ^ n \, \ exp (- \ lambda \, n \ overline {x}) \ times \ frac {\ beta ^ {\ alpha}} {\ Gamma (\ alpha)} \, \ lambda ^ {\ alfa-1} \, \ exp (- \ lambda \, \ beta)$

$\ Propto \ lambda ^ {(\ alpha + n) -1} \, \ exp (- \ lambda \, (\ beta + n \ overline {x})).$

Ahora el p densidad posterior se ha determinado hasta un constante normalizadora desaparecidos. Ya que tiene la forma de un pdf gamma, esto puede ser fácilmente rellenado, y se obtiene

$p (\ lambda) = \ mathrm {Gamma} (\ lambda \,; \, \ alpha + n, \ beta + n \ overline {x}).$

Aquí los parámetros α pueden interpretarse como el número de observaciones anteriores, y β como la suma de las observaciones anteriores.

Generación de variables aleatorias exponenciales

Un método conceptualmente muy simple para la generación exponencial variables aleatorias se basa en transformada inversa de muestreo: Dada una variable aleatoria U trazada desde el distribución uniforme en el intervalo unidad 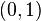$(0, 1)$ , La variable aleatoria

$T = F ^ {- 1} (U) \!$

tiene una distribución exponencial, donde 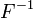$F ^ {- 1}$ es la función cuantil, definido por

$F ^ {- 1} (p) = \ frac {- \ ln (1-p)} {\ lambda}. \!$

Además, si T es uniforme en 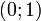$(0; 1)$ , También lo es 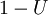$1-U$ . Esto significa que uno puede generar variables aleatorias exponenciales como sigue:

$T = \ frac {- \ ln U} {\ lambda}. \!$

Otros métodos para generar variables aleatorias exponenciales son discutidos por Knuth y Devroye.

La algoritmo zigurat es un método rápido para la generación de variables aleatorias exponenciales.

Distribuciones Relacionados

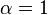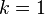Una distribución exponencial es un caso especial de una distribución gamma con $\ Alpha = 1$ (O $k = 1$ en función del conjunto de parámetros utilizados).
Tanto una distribución exponencial y una distribución gamma son casos especiales de la distribución de tipo fase.
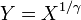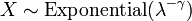$Y \ sim \ operatorname {Weibull} (\ gamma, \ lambda)$ , Es decir, Y tiene una Distribución de Weibull, si $Y = X ^ {1 / \ gamma} \,$ y $X \ sim \ operatorname {Exponencial} (\ lambda ^ {- \ gamma})$ . En particular, cada distribución exponencial es también una distribución de Weibull.
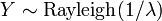$Y \ sim \ operatorname {} Rayleigh (1 / \ lambda)$ , Es decir, Y tiene una Distribución de Rayleigh, si $Y = \ sqrt {2X / \ lambda}$ y $X \ sim \ operatorname {Exponencial} (\ lambda)$ .
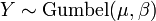$Y \ sim \ operatorname {Gumbel} (\ mu, \ beta)$ , Es decir, Y tiene una Distribución Gumbel si 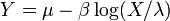$Y = \ mu - \ beta \ log (/ \ lambda X) \,$ y $X \ sim \ operatorname {Exponencial} (\ lambda)$ .
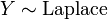$Y \ sim \ operatorname {Laplace}$ , Es decir, Y tiene una Distribución de Laplace, si 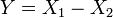$Y = x 1 - X_2 \,$ para dos distribuciones exponenciales independientes $X_1 \,$ y $X_2 \,$ .
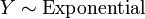$Y \ sim \ operatorname {Exponencial}$ , Es decir, Y tiene una distribución exponencial si $Y = \ min (x_1, \ dots, x_n)$ para distribuciones exponenciales independientes $X_i \,$ .
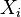$Y \ sim \ operatorname {} Uniforme (0,1)$ , Es decir, Y tiene una distribución uniforme si 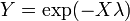$Y = \ exp (-X \ lambda) \,$ y $X \ sim \ operatorname {Exponencial} (\ lambda)$ .
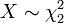$X \ sim \ chi_2 ^ 2$ , Es decir, X tiene una distribución chi-cuadrado con 2 grados de libertad, de ser $X \ sim \ operatorname {Exponencial} (\ lambda = 1/2) \, \;$ .
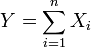Dejar $X_1 \ dots X_n \ sim \ operatorname {Exponencial} (\ lambda) \,$ ser distribuidos de manera exponencial e independiente y $Y = \ sum_ {i = 1} ^ n X_i \,$ . Entonces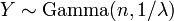 $Y \ sim \ operatorname {gamma} (n, 1 / \ lambda) \,$
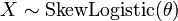$X sim \ operatorname {SkewLogistic} (\ theta) \ \,$ , A continuación, $\ Operatorname {log} (1 + e ^ {- X}) \ sim \ operatorname {Exponencial} (\ theta) \,$

Recuperado de " http://en.wikipedia.org/w/index.php?title=Exponential_distribution&oldid=195091990 "