Distribución de probabilidad

Una distribución de probabilidad describe los valores y las probabilidades de que una evento al azar puede tener lugar. Los valores deben cubrir todos los posibles resultados del evento, mientras que las probabilidades totales debe sumar exactamente 1, o 100%. Por ejemplo, una sola cara o cruz puede tomar valores Cara o Cruz con una probabilidad de exactamente media para cada uno; estos dos valores y dos probabilidades representan la distribución de probabilidad del evento único flipping moneda. Esta distribución se denomina distribución discreta porque hay una número contable de los resultados discretos con probabilidades positivas.

Una distribución continua describe los eventos en un rango continuo, donde la probabilidad de un resultado específico es cero. Por ejemplo, un dardo lanzado a una diana tiene esencialmente cero probabilidad de aterrizar en un punto específico, ya que un punto es extremadamente pequeña, pero tiene cierta probabilidad de aterrizar en un área determinada. La probabilidad de un aterrizaje en el área pequeña de la diana sería (esperemos) ser mayor que el aterrizaje en un área equivalente en otro lugar en el tablero. Una función suave que describe la probabilidad de aterrizaje en cualquier lugar de la diana es la distribución de probabilidad del evento de lanzamiento de dardos. La integral de la función de densidad de probabilidad (pdf) sobre toda el área de la diana (y, quizás, la pared que lo rodea) debe ser igual a 1, ya que cada dardo debe aterrizar en alguna parte.

El concepto de la distribución de probabilidad y las variables aleatorias que describen la base de la disciplina matemática de la teoría de probabilidad , y la ciencia de las estadísticas . Hay dispersión o variabilidad en casi cualquier valor que puede ser medido en una población (por ejemplo, altura de las personas, la durabilidad de un metal, etc.); casi todas las mediciones se hacen con alguna error intrínseco; en la física muchos procesos se describen probabilísticamente, desde el propiedades cinéticas de gases a la mecánica cuántica descripción de partículas fundamentales. Por estas y muchas otras razones, simples números son a menudo insuficientes para describir una cantidad, mientras que las distribuciones de probabilidad son a menudo modelos más apropiados. Hay, sin embargo, considerables complicaciones matemáticas en la manipulación de las distribuciones de probabilidad, ya que la mayoría estándar aritmética y manipulaciones algebraicas no se pueden aplicar.

Definiciones rigurosas

En teoría de la probabilidad , cada variable aleatoria puede ser atribuido a una función definida en un espacio de estados equipado con una distribución de probabilidad que asigna una probabilidad a cada subconjunto (más precisamente cada subconjunto medible) de su espacio de estado de tal manera que la axiomas de probabilidad son satisfechos. Es decir, las distribuciones de probabilidad son medidas de probabilidad definidas sobre un espacio de estados en lugar de la espacio de muestra. Una variable aleatoria define entonces una medida de probabilidad en el espacio de muestra mediante la asignación de un subconjunto del espacio de muestra de la probabilidad de su imagen inversa en el espacio de estado. En otras palabras, la distribución de probabilidad de una variable aleatoria es la impulsar medida de la distribución de probabilidad en el espacio de estado.

Distribuciones de probabilidad de variables aleatorias valorados real

Debido a una distribución de probabilidad Pr en la línea real está determinado por la probabilidad de estar en un intervalo semiabierto Pr (a, b], la distribución de probabilidad de una variable aleatoria de valor real X está completamente caracteriza por su función de distribución acumulativa:

Distribución de probabilidad discreta

Una distribución de probabilidad se llama discreta si su función de distribución acumulativa sólo aumenta en saltos.

La conjunto de todos los valores que una variable aleatoria discreta puede asumir con probabilidad no nula es o bien finito o infinito numerable porque la suma de uncountably muchos positivos números reales (que es el límite superior más pequeña del conjunto de todas las sumas parciales finitas) siempre diverge a infinito. Típicamente, el conjunto de valores posibles es discreta topológicamente en el sentido de que todos sus puntos son puntos aislados. Sin embargo, hay variables aleatorias discretas para que este conjunto numerable se densa en la recta real.

Distribuciones discretas se caracterizan por una función de probabilidad, de tal manera que

Distribución de probabilidad continua

Por una convención, una distribución de probabilidad se llama continua si su función de distribución acumulada es continua, lo que significa que pertenece a una variable aleatoria X para el que Pr [X = x] = 0 para todo x en R.

Otra convención se reserva el término distribución de probabilidad continua para distribuciones absolutamente continuas. Estas distribuciones se pueden caracterizar por una la función de densidad de probabilidad: un no negativo integrable Lebesgue función definida en los números reales tales que

Distribuciones discretas y algunas distribuciones continuas (como la escalera del diablo) no admiten una densidad tal.

Terminología

El apoyo de una distribución es el más pequeño conjunto cerrado cuyo complemento tiene probabilidad cero.

La distribución de probabilidad de la suma de dos variables aleatorias independientes es la convolución de cada uno de sus distribuciones.

La distribución de probabilidad de la diferencia de dos variables aleatorias es la correlación cruzada de cada uno de sus distribuciones.

Una variable aleatoria discreta es una variable aleatoria cuya distribución de probabilidad es discreto. Del mismo modo, una variable aleatoria continua es una variable aleatoria cuya distribución de probabilidad es continua.

Lista de distribuciones de probabilidad importantes

Ciertas variables aleatorias se producen muy a menudo en la teoría de probabilidades, en algunos casos debido a su aplicación a muchos procesos naturales y físicas, y en algunos casos debido a razones teóricas tales como la teorema del límite central, el Poisson teorema del límite, o propiedades como memorylessness u otro caracterizaciones. Sus distribuciones por lo tanto han adquirido especial importancia en la teoría de la probabilidad.

Distribuciones discretas

Con soporte finito

• La Distribución de Bernoulli, que toma valor 1 con probabilidad p y el valor 0 con probabilidad q = 1 - p.
• La Distribución Rademacher, que toma valor 1 con probabilidad 1/2 y el valor -1 con probabilidad 1/2.
• La distribución binomial describe el número de éxitos en una serie de independientes Sí / No experimentos.
• La distribución degenerada en x _0, donde X es seguro para tomar el valor x _0. Esto no parece aleatoria, sino que responde a la definición de la variable aleatoria . Es útil porque pone las variables deterministas y variables aleatorias en el mismo formalismo.
• La distribución uniforme discreta, donde todos los elementos de un finito conjunto son igualmente probables. Esto se supone que es la distribución de una moneda equilibrada, de una boquilla imparcial, una ruleta de casino o una cubierta bien barajado. Además, se puede usar mediciones de estados cuánticos para generar variables aleatorias uniformes. Todos estos son dispositivos "mecánicos" "física" o, sujeto a fallas de diseño o perturbaciones, por lo que la distribución uniforme es sólo una aproximación de su comportamiento. En las computadoras digitales, generadores de números pseudo-aleatorios se utilizan para producir una distribución uniforme discreta estadísticamente aleatorio.
• La distribución hipergeométrica, que describe el número de éxitos en el primer m de una serie de n Sí / No hay experimentos, si se conoce el número total de éxitos.
• La ley de Zipf o la distribución Zipf. Una distribución de ley de potencia discreto, el ejemplo más famoso de los cuales es la descripción de la frecuencia de las palabras en el idioma Inglés.
• La La ley de Zipf-Mandelbrot es una distribución de ley de potencia discreta que es una generalización de la Distribución Zipf.

Con el apoyo infinito

• La Distribución de Boltzmann, una distribución discreta importante en física estadística que describe las probabilidades de los diversos niveles discretos de energía de un sistema en equilibrio térmico. Tiene una continua analógica. Casos especiales incluyen:
  • La Distribución de Gibbs
  • La Distribución de Maxwell-Boltzmann
  • La Distribución de Bose-Einstein
  • La Distribución de Fermi-Dirac
• La distribución geométrica, una distribución discreta que describe el número de intentos necesarios para obtener el primer éxito en una serie de independientes Sí / No experimentos.

Distribución de Poisson

• La logarítmica (series) de distribución
• La distribución binomial negativa, una generalización de la distribución geométrica a la n-ésima éxito
• La distribución parabólica fractal
• La distribución de Poisson , que describe un gran número de eventos improbables individualmente que ocurren en un cierto intervalo de tiempo.

Distribución Skellam

• La Skellam distribución, la distribución de la diferencia entre dos variables aleatorias independientes de Poisson-distribuido
• La Distribución de Yule-Simon
• La distribución zeta tiene usos en estadística aplicada y mecánica estadística, y tal vez puede ser de interés para los teóricos de números. Es el Distribución Zipf para un número infinito de elementos.

Distribuciones continuas

Apoyado en un intervalo acotado

Distribución Beta

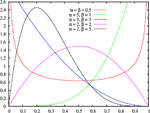
• La Distribución Beta en [0,1], de los cuales la distribución uniforme es un caso especial, y que es útil en la estimación de las probabilidades de éxito.

distribución uniforme continua

• La distribución uniforme continua en [a, b], donde todos los puntos en un intervalo finito son igualmente probables.
  • La distribución rectangular es una distribución uniforme en [-1 / 2,1 / 2].
• La Función delta de Dirac aunque no es estrictamente una función, es una forma limitante de muchas funciones de probabilidad continuas. Se representa una distribución de probabilidad discreta concentrado a 0 - una distribución degenerada - pero la notación trata como si se tratara de una distribución continua.
• La Distribución de Kent en la esfera tridimensional
• La Distribución Kumaraswamy es tan versátil como la distribución Beta, pero tiene formas simples cerradas tanto para el CDF y el pdf.
• La distribución logarítmica (continua)
• La distribución triangular en [a, b], un caso especial de que es la distribución de la suma de dos variables aleatorias distribuidas uniformemente (la convolución de dos distribuciones uniformes).
• La truncado distribución normal en [a, b]
• La Distribución U-cuadrática en [a, b]
• La distribución von Mises en el círculo
• La distribución von Mises-Fisher en la esfera N-dimensional tiene la distribución von Mises como un caso especial.
• La Distribución de Wigner semicírculo es importante en la teoría de la matrices aleatorias.

Apoyado en intervalos semi-infinitos, por lo general [0, ∞)

distribución chi-cuadrado

• La distribución chi
• La distribución chi no central
• La distribución de chi-cuadrado , que es la suma de los cuadrados de variables aleatorias gaussianas independientes n. Se trata de un caso especial de la distribución Gamma, y se utiliza en pruebas de bondad de ajuste en las estadísticas .
  • La inversa-chi-cuadrado de distribución
  • La no central chi-cuadrado de distribución
  • La escala-inversa-chi-cuadrado de distribución

Distribución exponencial

• La distribución exponencial , que describe el tiempo entre eventos aleatorios raras consecutivos en un proceso sin memoria.
• La F-distribución, que es la distribución de la relación de variables aleatorias distribuidas dos (normalizada) chi-cuadrado, utilizado en el análisis de varianza. (Denominado distribución prime beta cuando es el cociente de dos variables aleatorias de chi-cuadrado que no se normalizan dividiéndolos por sus números de grados de libertad.)
  • La no central F-distribución

Distribución Gamma

• La Distribución Gamma, que describe el tiempo hasta que se producen los eventos aleatorios raras n consecutivos en un proceso sin memoria.
  • La Distribución de Erlang, que es un caso especial de la distribución gamma con parámetro de forma integral, desarrollado para predecir los tiempos de espera en sistemas de colas.
  • La distribución inversa-gamma
• La distribución normal plegada
• La medio-normal de distribución
• La distribución gaussiana inversa, también conocido como la distribución Wald
• La Distribución de Lévy
• La distribución log-logística
• La log-normal de distribución, que describe las variables que se pueden modelar como el producto de muchas pequeñas variables positivas independientes.

Distribución de Pareto

• La Distribución de Pareto, o la distribución "ley de potencias", utilizada en el análisis de los datos financieros y comportamiento crítico.
• La distribución de Pearson Tipo III (ver Distribuciones de Pearson)
• La Distribución de Rayleigh
• La Distribución de la mezcla de Rayleigh
• La Distribución de arroz
• La Colofonia distribución Rammler - usado para describir la distribución de tamaño de partícula de las partículas generadas por molienda, fresado y las operaciones de trituración.
• La distribución Gumbel tipo 2
• La Distribución de Weibull, de los cuales la distribución exponencial es un caso especial, se utiliza para modelar la vida útil de los dispositivos técnicos.

Con el apoyo de toda la recta real

Distribución de Cauchy

Distribución de Laplace

Distribución Levy

Distribución normal

• La Distribución de Cauchy, un ejemplo de una distribución que no tiene una valor esperado o una varianza . En física se le suele llamar un Perfil de Lorentz, y se asocia con muchos procesos, incluyendo distribución de energía de resonancia, impacto y natural ampliación de la línea espectral y cuadrática ampliación de la línea cruda.
• La Fisher-Tippett, valor extremo, o log-Weibull distribución
  • La Distribución Gumbel, un caso especial de la distribución de Fisher-Tippett
• Z-distribución de Fisher
• La distribución generalizada de valores extremos
• La distribución hiperbólica
• La distribución secante hiperbólica
• La Distribución Landau
• La Distribución de Laplace
• La Distribución alfa estable sesgo Lévy se utiliza a menudo para caracterizar los datos financieros y comportamiento crítico.
• La distribución mapa-Airy
• La distribución normal , también llamado el gaussiana o la curva de campana. Es ubicuo en la naturaleza y las estadísticas debido a la teorema del límite central: cada variable que puede ser modelada como una suma de muchas pequeñas variables independientes es aproximadamente normal.
• La Distribución Pearson tipo IV (véase Distribuciones de Pearson)
• La distribución t de Student , útiles para estimar medios desconocidos de las poblaciones de Gauss.
  • La no central distribución t
• La distribución Gumbel tipo 1
• La Distribución Voigt, o perfil de Voigt, es la convolución de una distribución normal y una Distribución de Cauchy. Se encuentra en la espectroscopia cuando perfiles de líneas espectrales se amplían por una mezcla de Lorentz y Doppler ampliar mecanismos.

Distribuciones conjuntas

Para cualquier conjunto de variables aleatorias independientes del función de densidad de probabilidad de su distribución conjunta es el producto de sus funciones individuales de densidad.

Distribuciones de matriz con valores

• Distribución Wishart
• distribución normal matriz
• matriz de distribución t
• Distribución T-cuadrado de Hotelling