
Máximo común divisor
Acerca de este escuelas selección Wikipedia
SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . Una buena manera de ayudar a otros niños es mediante el patrocinio de un niño
En matemáticas , el máximo común divisor (mcd), a veces conocido como el máximo común divisor (MCD) o el factor más alto común (HCF), de dos distintos de cero enteros , es el mayor entero positivo que divide ambos números sin resto.
Visión de conjunto
El máximo común divisor de a y b se escribe como gcd (a, b), o, a veces simplemente como (a, b). Por ejemplo, mcd (12, 18) = 6, mcd (-4, 14) = 2 y mcd (5, 0) = 5. Dos números son llamados primos entre sí o primos entre si su máximo común divisor es igual a 1. Por ejemplo, 9 y 28 son primos entre sí.
El máximo común divisor es útil para reducir fracciones vulgares ser en su mínima expresión. Por ejemplo, gcd (42, 56) = 14, por lo tanto,
Cálculo del mcd
Máximo común divisor pueden en principio ser calculadas mediante la determinación de la factores primos de los dos números y la comparación de factores, como en el siguiente ejemplo: para calcular mcd (18,84), nos encontramos con los factores primos de 18 = 2 · 3 2 y 84 = 2 2 · 3 · 7 y observe que el " solapamiento "de las dos expresiones es 2 · 3; así que mcd (18,84) = 6. En la práctica, este método sólo es viable para un número muy pequeño; computar factores primos en general toma demasiado tiempo.
Un método mucho más eficiente es la Algoritmo de Euclides, que utiliza el algoritmo de la división en combinación con la observación de que el máximo común divisor de dos números también divide su diferencia: divide 84 por 18 para obtener un cociente de 4 y un resto de 12. Luego, divida 18 por 12 para obtener un cociente de 1 y un resto de 6 . Luego divida 12 por 6 para obtener un residuo de 0, lo que significa que 6 es el máximo común divisor.
La serie de cocientes generados por el algoritmo de Euclides componer una fracción continua.
Si ayb no son ambos cero, el máximo común divisor de ayb se pueden calcular utilizando mínimo común múltiplo (lcm) de a y b:
Propiedades
- Cada común divisor de a y b es un divisor de gcd (a, b).
- mcd (a, b), donde a y b no son ambos cero, se puede definir alternativa y equivalente como el menor entero positivo d que se puede escribir en la forma d = a + b · p · q donde p y q son números enteros . Esta expresión se llama Identidad de Bézout. Números p y q como esta se pueden calcular con la extendido algoritmo de Euclides.
- gcd (a, 0) = | a |, para un ≠ 0, ya que cualquier número es un divisor de 0, y el mayor divisor de a es | a |. Esto se utiliza generalmente como el caso base en el algoritmo de Euclides.
- Si una se divide el producto b · c, y mcd (a, b) = d, entonces a / d divide a c.
- Si m es un entero no negativo, entonces mcd (m · a, m · b) = m · mcd (a, b).
- Si m es cualquier número entero, entonces gcd (a + m · b, b) = gcd (a, b). Si m es un divisor común distinto de cero de A y B, a continuación, gcd (a / m, b / m) = gcd (a, b) / m.
- El mcd es un función multiplicadora en el siguiente sentido: si un 1 y un 2 son primos entre sí, entonces mcd (a 1 · a 2, b) = mcd (a 1, b) · mcd (a 2, b).
- El mcd es conmutativa función: mcd (a, b) = mcd (b, a).
- El mcd es un asociativa función: mcd (a, mcd (b, c)) = mcd (mcd (a, b), c).
- El mcd de tres números puede ser computado como mcd (a, b, c) = mcd (mcd (a, b), c), o de alguna manera diferente a través de conmutatividad y asociatividad. Esto se puede ampliar a cualquier número de números.
- mcd (a, b) está estrechamente relacionado con la menos común múltiplo mcm (a, b): tenemos
- mcd (a, b) · mcm (a, b) = a · b.
- Esta fórmula se utiliza a menudo para calcular múltiplos menos comunes: uno calcula primero el mcd con el algoritmo de Euclides y luego divide el producto de los números dados por su mcd. Las siguientes versiones de Distributivity ser cierto:
- mcd (a, mcm (b, c)) = mcm (mcd (a, b), mcd (a, c))
- mcm (a, mcd (b, c)) = mcd (mcm (a, b), mcm (a, c)).
- Es útil definir gcd (0, 0) = 0 y lcm (0, 0) = 0, porque entonces los números naturales se convierten en una completo distributivo celosía con mcd como se encuentran y mcm como unirse a la operación. Esta extensión de la definición también es compatible con la generalización para los anillos conmutativos que figuran a continuación.
- En un sistema de coordenadas cartesianas , gcd (a, b) puede ser interpretado como el número de puntos con coordenadas integrales en la línea recta que une los puntos (0, 0) y (a, b), con exclusión de (0, 0).
Las probabilidades y valor esperado
La probabilidad de que dos elegidos al azar enteros (sin límite)  y
y  tener un máximo común divisor dado
tener un máximo común divisor dado  es
es 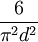 . Así se desprende de la caracterización de
. Así se desprende de la caracterización de 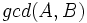 como el número entero
como el número entero  de tal manera que
de tal manera que 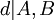 y
y 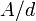 y
y 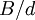 son primos entre sí. La probabilidad de que dos números enteros compartir un factor
son primos entre sí. La probabilidad de que dos números enteros compartir un factor  es
es 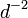 . La probabilidad de que dos enteros son primos entre sí es
. La probabilidad de que dos enteros son primos entre sí es  . (Ver coprimeros para una derivación.)
. (Ver coprimeros para una derivación.)
Usando esta información, el valor esperado de la función más común divisor puede ser calculado. Esto es
Esta última es la suma Serie armónica, que diverge. Por lo tanto no está bien definido el valor esperado de el máximo común divisor de dos variables. Este no es el caso en general, sin embargo. Para el máximo común divisor de 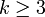 variables, el valor esperado es bien definidos, y por el argumento anterior, es
variables, el valor esperado es bien definidos, y por el argumento anterior, es
donde 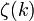 es el Función zeta de Riemann.
es el Función zeta de Riemann.
Para  , Esto es aproximadamente igual a 1,3684. Para
, Esto es aproximadamente igual a 1,3684. Para 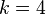 , Que es de aproximadamente 1,1106.
, Que es de aproximadamente 1,1106.
si todos los enteros x se limitan como 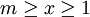 a continuación, los resultados pueden ser extendidos a
a continuación, los resultados pueden ser extendidos a
donde 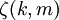 es el Función zeta de Hurwitz.
es el Función zeta de Hurwitz.
si es diferente  'S son conocidos por diferentes
'S son conocidos por diferentes  entonces el más bajo
entonces el más bajo  es tomado.
es tomado.
El mcd de anillos conmutativos
El máximo común divisor se puede definir en términos más generales de los elementos de una arbitraria anillo conmutativo .
Si R es un anillo conmutativo, y a y b son en I, a continuación, un elemento de R d se llama un divisor común de A y B si se divide tanto a como b (es decir, si hay elementos X e Y en R tal que d · x = a y d · y = b). Si d es un divisor común de A y B, y cada común divisor de a y b d divide, a continuación, d se llama un máximo común divisor de a y b.
Tenga en cuenta que con esta definición, dos elementos A y B pueden muy bien tener varios divisores más comunes, o ninguno en absoluto. Pero si R es una dominio de integridad entonces dos de MCD de A y B deben ser elementos asociados. Además, si R es una dominio de factorización única, entonces cualquiera de los dos elementos tienen una mcd. Si R es una Dominio euclidiano entonces una forma de el algoritmo de Euclides se pueden utilizar para calcular los divisores mayor comunes.
El siguiente es un ejemplo de un dominio integral con dos elementos que no tienen un mcd:
Los elementos 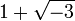 y
y  son dos "divisores comunes máximas" (es decir, cualquier divisor común que es un múltiplo de 2 se asocia a 2, lo mismo vale para
son dos "divisores comunes máximas" (es decir, cualquier divisor común que es un múltiplo de 2 se asocia a 2, lo mismo vale para 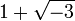 ), Pero que no están asociados, así que no hay máximo común divisor de a y b.
), Pero que no están asociados, así que no hay máximo común divisor de a y b.
En correspondencia con la propiedad de Bezout podemos, en cualquier anillo conmutativo, considere la colección de elementos de la forma  , Donde p y q rango sobre el anillo. Este es el ideal generado por A y B, y se denota simplemente
, Donde p y q rango sobre el anillo. Este es el ideal generado por A y B, y se denota simplemente  . En un anillo de todos cuyos ideales son principales (un dominio de ideales principales o PID), este ideal será idéntico con el conjunto de múltiplos de algún elemento del anillo d; entonces este d es un máximo común divisor de a y b. Pero el ideal
. En un anillo de todos cuyos ideales son principales (un dominio de ideales principales o PID), este ideal será idéntico con el conjunto de múltiplos de algún elemento del anillo d; entonces este d es un máximo común divisor de a y b. Pero el ideal  puede ser útil incluso cuando no hay ningún máximo común divisor de a y b. (Ciertamente, Ernst Kummer utiliza este ideal como sustituto de un mcd en su tratamiento del último teorema de Fermat , aunque él lo imaginó como el conjunto de múltiplos de algún hipotético, o ideal, elemento de anillo d, de ahí el término anillo teórico.)
puede ser útil incluso cuando no hay ningún máximo común divisor de a y b. (Ciertamente, Ernst Kummer utiliza este ideal como sustituto de un mcd en su tratamiento del último teorema de Fermat , aunque él lo imaginó como el conjunto de múltiplos de algún hipotético, o ideal, elemento de anillo d, de ahí el término anillo teórico.)



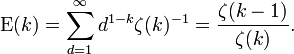
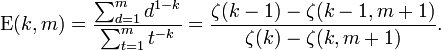
![R = \ mathbb {Z} \ left [\ sqrt {-3} \ right], \ quad a = 4 = 2 \ cdot 2 = \ left (1+ \ sqrt {-3} \ right) \ left (1- \ sqrt {-3} \ right), \ quad b = \ left (1+ \ sqrt {-3} \ right) \ cdot 2.](../../images/184/18487.png)
