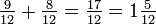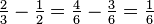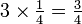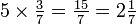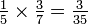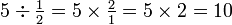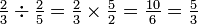Fracción (matemáticas)

Temas relacionados: Matemáticas

Acerca de este escuelas selección Wikipedia

SOS Children, que corre cerca de 200 sos escuelas en el mundo en desarrollo, organizó esta selección. SOS Children ha cuidado de niños en África durante cuarenta años. ¿Puedes ayudar a su trabajo en África ?

Una torta con cuarto eliminado. Se muestran las tres cuartas partes restantes.

En matemáticas , una fracción (del latín fractus, roto) es un concepto de un proporcional relación entre una parte de objeto y el conjunto de objetos. Cada fracción se compone de un denominador (parte inferior) y un numerador (arriba), que representa (respectivamente) el número de partes iguales que un objeto se divide en, y el número de las partes indicadas para la fracción particular.

Para ejemplo, la fracción ¾ podría ser usado para representar tres partes iguales de un objeto entero, se dividió en cuatro partes iguales. Debido a que es imposible dividir algo en partes iguales a cero, cero nunca puede ser el denominador de una fracción (ver división por cero). Una fracción con igual numerador y el denominador es igual a uno (por ejemplo, 5.5 = 1) y la forma de fracción es rara vez, o nunca, da como resultado final.

Una fracción es un ejemplo de un tipo específico de relación, en la que los dos números se relacionan en una relación de parte a todo, en lugar de como una relación comparativa entre dos cantidades separadas. Una fracción es una cociente de números , la cantidad obtenida cuando el numerador se divide por el denominador. Así ¾ representa tres dividido por cuatro, en decimales 0.75, como un porcentaje del 75%. Las tres partes iguales de la torta son 75% de toda la torta.

En matemáticas superiores, una fracción es visto como un elemento de un campo de fracciones.

Históricamente, cualquier número que no representa en su conjunto se llama una "fracción". Los números que ahora llamamos "decimales" se llamaban originalmente "fracciones decimales"; los números que ahora llamamos "fracciones" fueron llamados "fracciones vulgares", la palabra "vulgar", que significa "lugar común".

El numerador y el denominador de una fracción pueden estar separados por una línea inclinada llamado solidus o recortar, por ejemplo ¾, o puede ser escrito por encima y debajo de una línea horizontal llamado vinculum, así: $\ Tfrac {3} {4}$ .

El solidus se puede omitir desde el estilo de inclinación (por ejemplo, ³ ₄₎ donde el espacio es corto y el significado es evidente a partir del contexto, por ejemplo, en señales de tráfico en algunos países.

Las fracciones que se utilizan con más frecuencia cuando el denominador es relativamente pequeño. Es más fácil de multiplicar 32 por 3/16 de hacer el mismo cálculo usando equivalente decimal de la fracción (0,1875). También es más preciso multiplicar por 15 ⅓, por ejemplo, de lo que es multiplicar 15 por una aproximación decimal de un tercio. Para cambiar una fracción a un decimal, divide el numerador entre el denominador, y acabe con la exactitud deseada.

Las fracciones también son números racionales, en lo que significa que el denominador y el numerador son números enteros.

La palabra también se utiliza en las expresiones relacionadas, tales como fracción continua y algebraica fracción ver casos especiales siguientes.

Formas de fracciones

Vulgar, adecuada, y fracciones impropias

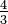Una fracción vulgar (o fracción común) es un número racional escrita como una número entero (el numerador) dividido por un número entero distinto de cero (el denominador), por ejemplo, $\ Tfrac {1} {3}$ , $\ Tfrac {3} {4}$ y $\ Tfrac {4} {3}$ .

Una fracción vulgar se dice que es una fracción adecuada si el valor absoluto del numerador es menor que el valor absoluto del denominador, es decir, si el valor absoluto de la totalidad de la fracción es menor que 1 (por ejemplo, $\ Tfrac {4} {9}$ ), Pero una fracción impropia (US, británico o australiano) o de arriba fracción pesada (British solamente) si el valor absoluto del numerador es mayor que o igual al valor absoluto del denominador (por ejemplo, $\ Tfrac {9} {7}$ ).

Los números mixtos

Un número mixto es la suma de un número entero y una fracción propia. Por ejemplo, al referirse a dos pasteles enteros y tres cuartas partes de otro pastel, el todo y las partes fraccionarias de la serie están escritos junto a la otra: 2 + 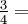$\ Tfrac {3} {4} =$ 2 $\ Tfrac {3} {4}$ .

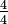Una fracción impropia puede ser considerado como otra manera de escribir un número mixto; en el "2 $\ Tfrac {3} {4}$ "Ejemplo anterior, imagine que los dos pasteles enteros se dividieron en cuatro partes. Cada uno contribuye enteras torta $\ Tfrac {4} {4}$ al total, por lo 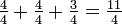$\ Tfrac {4} {4} + \ tfrac {4} {4} + \ tfrac {3} {4} = \ tfrac {11} {4}$ es otra manera de escribir 2 $\ Tfrac {3} {4}$ .

Un número mixto se puede convertir en una fracción impropia en tres pasos:

Multiplicar la parte entera por el denominador de la parte fraccionaria.
Añadir el numerador de la parte fraccionaria de ese producto.
La suma resultante es el numerador de la nueva (inadecuado) fracción, y el nuevo denominador es el mismo que el de la parte fraccionaria del número mixto.

Del mismo modo, una fracción impropia se puede convertir en un número mixto:

Divide el numerador entre el denominador.
El cociente (sin resto) se convierte en toda la parte y el resto se convierte en el numerador de la parte fraccionaria.
El nuevo denominador es el mismo que el de la fracción impropia originales.

Fracciones equivalentes

Multiplicando el numerador y el denominador de una fracción por los mismos resultados (no cero) número en una nueva fracción que se dice que es equivalente a la fracción original. La palabra equivalente significa que las dos fracciones tienen el mismo valor. Esto es cierto porque para cualquier número $n$ , Multiplicando por $\ Tfrac {n} {n}$ que realmente se multiplica por uno, y cualquier número multiplicado por uno tiene el mismo valor que el número original. Por ejemplo, considere la fracción $\ Tfrac {1} {2}$ : Cuando el numerador y el denominador son ambos multiplican por 2, el resultado es $\ Tfrac {2} {4}$ , Que tiene el mismo valor (0,5) como $\ Tfrac {1} {2}$ . Para representar esto visualmente, imagina cortar el ejemplo torta en cuatro pedazos; dos de las piezas ( $\ Tfrac {2} {4}$ ) Constituyen la mitad de la torta ( $\ Tfrac {1} {2}$ ).

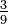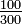Por ejemplo: $\ Tfrac {1} {3}$ , $\ Tfrac {2} {6}$ , $\ Tfrac {3} {9}$ y $\ Tfrac {100} {300}$ son todas las fracciones equivalentes.

Dividiendo el numerador y el denominador de una fracción por el mismo número distinto de cero también producirá una fracción equivalente. esto se llama la reducción o la simplificación de la fracción. Una fracción en la que el numerador y el denominador no tienen factores en común (excepto 1) se dice que es irreducible o en sus términos más bajos o más simples. Por ejemplo, 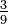$\ Tfrac {3} {9}$ no está en su mínima expresión porque ambos 3 y 9 se puede dividir exactamente por 3. Por el contrario, 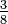$\ Tfrac {3} {8}$ es más bajo en términos, el único número que es un factor tanto de 3 y 8 es 1.

Recíprocos y el "denominador invisible"

La recíproco de una fracción es otra fracción con el numerador y el denominador invertido. El recíproco de $\ Tfrac {3} {7}$ , Por ejemplo, es $\ Tfrac {7} {3}$ .

Debido a que cualquier número dividido por 1 resultados en el mismo número, es posible escribir cualquier número entero como una fracción mediante el uso de 1 como denominador: 17 = 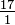$\ Tfrac {17} {1}$ (1 se refiere a veces como el "denominador invisible"). Por lo tanto, a excepción de cero, cada fracción o número entero tiene un recíproco. El recíproco de 17 sería $\ Tfrac {1} {17}$ .

Fracciones complejas

Una fracción complejo (compuesto o fracción) es una fracción en la que el numerador y el denominador contienen una fracción. Por ejemplo, 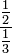$\ Cfrac {\ tfrac {1} {2}} {\ tfrac {1} {3}}$ es una fracción compleja. Para simplificar una fracción compleja, se divide el numerador entre el denominador, como con cualquier otra fracción: $\ Cfrac {\ tfrac {1} {2}} {\ tfrac {1} {3}} = \ tfrac {3} {2}$ .

Aritméticas con fracciones

Las fracciones, como números enteros, obedecen a la conmutativa , asociativa , y leyes distributivas, y el Estado contra la división por cero.

La comparación de fracciones

La comparación de fracciones con el mismo denominador sólo requiere comparar los numeradores.

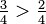$\ Tfrac {3} {4}> \ tfrac {2} {4}$ como $3> 2$ .

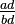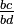Para comparar fracciones con diferentes denominadores, éstos se convierten en un denominador común: comparar $\ Tfrac {a} {b}$ y $\ Tfrac {c} {d}$ , Éstos se convierten a $\ Tfrac {ad} {bd}$ y $\ Tfrac {bc} {bd}$ , Donde bd es el producto de los denominadores, y luego el numeradores AD y BC se comparan.

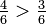
$\ Tfrac {2} {3}$ ? $\ Tfrac {1} {2}$ da $\ Tfrac {4} {6}> \ tfrac {3} {6}$

Este método también se conoce como el método de "cross-multiplicar", que puede ser explicado por la multiplicación de los números superior e inferior en sentido transversal. El producto de los denominadores se utiliza como un común (pero no es necesario el menos común) denominador.

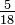$\ Tfrac {5} {18}$ ? $\ Tfrac {4} {17}$

Multiplique 17 por 5 y 18 por 4. Coloque los productos de las ecuaciones en la parte superior de los denominadores. El número más alto identifica la fracción más grande. Por lo tanto 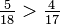$\ Tfrac {5} {18}> \ tfrac {4} {17}$ como 17 × 5 = 85 es mayor que 18 × 4 = 72.

Con el fin de trabajar con números más pequeños, el mínimo común denominador se utiliza en lugar del producto. Las fracciones se convierten en fracciones con el mínimo común denominador, y luego los numeradores se comparan.

$\ Tfrac {5} {6}$ ? $\ Tfrac {3} {4}$ da $\ Tfrac {10} {12}> \ tfrac {8} {12}$

Algunos textos de matemáticas basadas en estándares como Matemáticas Connected omitir la instrucción de los denominadores menos comunes por completo. Ese texto se presenta el uso de "tiras de fracciones" (una tira de papel doblado en fracciones) o "fracciones de referencia" como un medio contra el que una fracción como dos quintas partes se pueden comparar. Si bien esos métodos pueden ser útiles para construir la comprensión conceptual, que son controvertidos, ya que no son efectivos más allá del nivel de la escuela primaria, y este tipo de textos se complementan a menudo por profesores con el método estándar.

Adición

La primera regla de la adición es que sólo como cantidades pueden añadirse; por ejemplo, diversas cantidades de trimestres. A diferencia de las cantidades, como la adición de terceras partes a los cuartos, primero se debe convertir a gustar cantidades como se describe a continuación:

Sumar cantidades

Imagine un bolsillo que contiene dos trimestres, y otro bolsillo que contiene tres cuartas partes; en total, hay cinco trimestres. Desde cuatro cuartos es equivalente a un (dólar), esto puede representarse como sigue:

$\ Tfrac24 + \ tfrac34 = \ tfrac54 = 1 \ tfrac14$ .

Si $\ Tfrac12$ de un pastel es que se añade a $\ Tfrac14$ de un pastel, las piezas deben ser convertidos en cantidades comparables, como la torta de octavos o cuartos de pastel.

Agregando a diferencia de cantidades

Para sumar fracciones que contienen a diferencia de cantidades (por ejemplo, cuartos y tercios), es necesario convertir todas las cantidades que gusta cantidades. Es fácil calcular el tipo de fracción convertir; simplemente multiplica los dos denominadores (número inferior) de cada fracción.

Para agregar cuartos a terceras partes, los dos tipos de fracción se convierten en $\ Tfrac14 \ times \ tfrac13 = \ {12} tfrac1$ (doceavas partes).

Considere agregar las siguientes dos cantidades:

$\ Tfrac34 + \ tfrac23$

En primer lugar, convertir 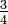$\ Tfrac34$ en doceavos multiplicando el numerador y el denominador por tres: $\ Tfrac34 \ times \ tfrac33 = \ {12} tfrac9$ . Tenga en cuenta que 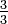$\ Tfrac33$ es equivalente a 1, lo que demuestra que 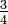$\ Tfrac34$ es equivalente a la resultante $\ Tfrac9 {12}$

En segundo lugar, convertir $\ Tfrac23$ en doceavos multiplicando el numerador y el denominador por cuatro: 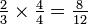$\ Tfrac23 \ times \ tfrac44 = \ {12} tfrac8$ . Tenga en cuenta que $\ Tfrac44$ es equivalente a 1, lo que demuestra que $\ Tfrac23$ es equivalente a la resultante $\ Tfrac8 {12}$

Ahora se puede observar que:

$\ Tfrac34 + \ tfrac23$

es equivalente a:

$\ Tfrac9 {12} + \ tfrac8 {12} = \ tfrac {17} {12} = 1 \ tfrac5 {12}$

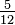Este método funciona siempre, pero a veces hay un denominador más pequeño que se puede utilizar (denominador un mínimo común). Por ejemplo, para añadir $\ Tfrac {3} {4}$ y $\ Tfrac {5} {12}$ el denominador se puede utilizar 48 (el producto de 4 y 12), pero el denominador más pequeño 12 también puede ser utilizado, siendo el el mínimo común múltiplo de 4 y 12.

$\ Tfrac34 + \ tfrac {5} {12} = \ tfrac {9} {12} + \ tfrac {5} {12} = \ tfrac {14} {12} = \ tfrac76 = 1 \ tfrac16$

Sustracción

El proceso para restar fracciones es, en esencia, el mismo que el de la adición de ellos: encontrar un denominador común, y cambiar cada fracción a una fracción equivalente con el denominador común elegido. La fracción resultante tendrá que denominador y numerador será el resultado de restar los numeradores de las fracciones originales. Por ejemplo,

$\ Tfrac23- \ tfrac12 = \ tfrac46- \ tfrac36 = \ tfrac16$

Multiplicación

Cuando multiplicar o dividir, podría ser posible seleccionar para cancelar abajo transversalmente múltiplos que comparten un factor común. Por ejemplo:

1/ 2 1 X 1/ 7 1 = 1.1 X 1.1. A continuación se explica cómo llevar a cabo esta ecuación.

La multiplicación por números enteros

Teniendo en cuenta el ejemplo de la torta antes, si usted tiene un cuarto de la torta y se multiplica la cantidad por tres, entonces usted termina con las tres cuartas partes. Podemos escribir este numéricamente como sigue:

$\ TextStyle {3 \ épocas {1 \ over 4} = {3 \ over 4}} \, \!$

Como otro ejemplo, supongamos que cinco personas trabajan durante tres horas de una jornada de siete hora (es decir. Por tres séptimas partes de la jornada de trabajo). En total, se han trabajado durante 15 horas (5 x 3 horas cada una), o 15/7 de un día. Desde 7/7 de un día es un día entero y 14/7 es de dos días, luego en total, habrán trabajado durante 2 días y un séptimo de un día. Numéricamente:

$\ TextStyle {5 \ épocas {3} \ sobre 7 = {15} \ sobre 7 = 2 {1 \ over 7}} \, \!$

La multiplicación por fracciones

Teniendo en cuenta el ejemplo de la torta antes, si usted tiene un cuarto de la torta y se multiplica la cantidad por un tercero, entonces usted termina con una doceava parte de la torta. En otras palabras, un tercio de un cuarto (o un tercio veces cuarto) es un doceavo. ¿Por qué? Debido a que estamos dividiendo cada trimestre en tres pedazos, y cuatro trimestres veces tres hace 12 partes (o doceavas partes). Podemos escribir este numéricamente como sigue:

$\ TextStyle {{1 \ más de 3} \ épocas {1 \ over 4} = {1 \ over 12}} \, \!$

Como otro ejemplo, supongamos que cinco personas hacen un trabajo igual cantidad que asciende a tres horas de una jornada de siete horas del día. Cada persona va a haber hecho una quinta parte de la obra, por lo que habrá trabajado para un quinto de las tres séptimas partes de un día. Numéricamente:

$\ TextStyle {{1 \ más de 5} \ épocas {3} \ sobre 7 = {3 \ mayores de 35 años}} \, \!$

Regla general

Usted puede haber notado que cuando multiplicamos fracciones, multiplicamos los dos numeradores (los números de arriba) para hacer el nuevo numerador, y se multiplican los dos denominadores (los números abajo) para que el nuevo denominador. Por ejemplo:

$\ TextStyle {{5 \ más de 6} \ épocas {7 \ más de 8} = {5 \ veces 7 \ más de 6 \ Tiempos 8} = {35 \ over 48}} \, \!$

La multiplicación por números mixtos

Al multiplicar números mixtos, es mejor para convertir la parte entera del número mixto en una fracción. Por ejemplo:

$\ TextStyle {3 \ times 2 {3} \ sobre 4 = 3 \ times \ left ({{8 \ over 4} + {3 \ over 4}} \ right) = 3 \ épocas {11 \ más de 4} = { 33 \ over 4} = 8 {1 \ over 4}} \, \!$

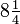En otras palabras, $\ Estilo de texto {2 {3 \ over 4}}$ es lo mismo que $\ Estilo de texto {({8 \ over 4} + {3 \ over 4})}$ , Lo que hace 11 trimestres en total (porque 2 tortas, cada división en cuartos hace 8/4 del total) y 33 trimestres $\ Estilo de texto {8 {1 \ over 4}}$ , Ya que 8 tortas, cada uno hecho de cuartos, tiene 32 cuartos en total.

División

Para dividir por una fracción, simplemente multiplica por el recíproco de esa fracción.

$\ TextStyle {5 \ div {1 \ over 2} = 5 \ veces {2 \ más de 1} = 5 \ Tiempos 2 = 10}$

$\ Estilo de texto {{2 \ over 3} \ div {2 \ over 5} = {2 \ over 3} \ épocas {5} \ sobre 2 = {10} \ sobre 6 = {5 \ over 3}}$

Para entender por qué esto funciona, considere lo siguiente:

Pregunta, ¿tiene

$\ Estilo de texto {\ frac ab \ div \ frac cd = \ frac ab \ times \ frac dc}$

Dada / Aceptado

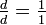I. Cualquier número dividido por sí mismo es uno (por ejemplo, $\ Estilo de texto {\ frac d d = \ frac 1 1}$ )

II. Cuando un número se multiplica por uno que no cambia (por ejemplo, $\ Estilo de texto {\ frac ab \ times \ frac 1 1 = \ frac ab \ times \ frac dd = \ frac ab}$ )

III. Si dos fracciones tienen denominadores comunes, entonces los numeradores se pueden dividir para encontrar el cociente (por ejemplo, $\ Estilo de texto {\ frac {ad} {bd} \ div \ frac {bc} {bd} = ad \ div bc}$ )

Prueba

1. $\ Estilo de texto {\ frac {a} {b} \ div \ frac {c} {d}}$ , Problema

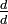2. $\ Estilo de texto {\ frac {ad} {bd} \ div \ frac {bc} {bd}}$ , Multiplicado la primera fracción por $\ Estilo de texto {\ frac d d}$ y la segunda fracción por 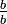$\ Estilo de texto {\ frac b b}$ , Lo que es lo mismo que multiplicar por uno, y aceptada (I y II) no cambia el valor de la fracción

Nota: Estos valores de uno fueron elegidos por lo que las fracciones tendrían un denominador común; bd es el denominador común.

3. $\ Estilo de texto {\ frac {ad} {bd} \ div \ frac {bc} {bd} = ad \ div bc}$ , Por lo que se dio en (III)

4. 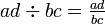$\ Estilo de texto {ad \ div bc = \ frac {ad} {bc}}$ , Notación Cambiado

5. 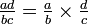$\ Estilo de texto {\ frac {ad} {bc} = \ frac ab \ times \ frac dc}$ , Puede ser visto

6. 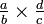$\ Estilo de texto {\ frac una b \ times \ frac d c}$ , Solución

Hace unos 4.000 años los egipcios dividieron con fracciones usando métodos ligeramente diferentes, usando múltiplos menos comunes con fracciones unitarias.

La conversión de decimales que se repiten a fracciones

Los números decimales, mientras que sin duda más útil trabajar con la hora de realizar los cálculos, carecen de la misma clase de precisión que las fracciones regulares (como se explica en este artículo) tienen. A veces se requiere un número infinito de decimales para transmitir el mismo tipo de precisión. Por lo tanto, a menudo es útil para convertir decimales en fracciones de repetición.

Para los patrones de repetición más, una simple división del patrón por el mismo número de nueves como números se ha será suficiente. Por ejemplo (el patrón se resalta en negrita):

0. 5 55 ... = 5/9

0. 264 264 264 ... 264/999 =

0. 6291 62916291 ... = 6291/9999

En ceros casos preceden al patrón, de punta en blanco se sufijo por el mismo número de ceros:

0,0 5 55 ... = 5/90

0.000 392 392 392 ... 392/999000 =

0.00 12 1212 ... = 12/9900

En el caso de un conjunto no repetitivo de decimales preceden el patrón (por ejemplo, 0,1523 987 987 987 ...), debemos equiparar como la suma de las partes no repetir y repetir:

0.1523 + 0.0000987987987 ...

A continuación, convertir ambos a las fracciones. Desde la primera parte no se repite, no se convierte de acuerdo con el patrón dado anteriormente:

1523/10000 + 987/9990000

Añadimos estas fracciones expresando ambos con un divisor común ...

1521477/9990000 + 987/9990000

Y agregarlos.

1522464/9990000

Finalmente, simplificamos:

31718/208125

Casos especiales

Una fracción es una fracción unidad vulgar con un numerador de 1, por ejemplo, $\ Tfrac {1} {7}$ .

Una Fracción egipcio es la suma de fracciones unitarias distintas, por ejemplo, 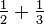$\ Tfrac {1} {2} + \ tfrac {1} {3}$ .

La diádica fracción es una fracción vulgar en el que el denominador es una potencia de dos, por ejemplo, 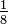$\ Tfrac {1} {8}$ .

Una expresión que tiene la forma de una fracción, pero en realidad representa la división por o en un número irracional a veces se denomina "fracción irracional". Un ejemplo común es $\ Estilo de texto {\ frac {\ pi} {2}}$ , La medida de arco de un ángulo recto.

Los números racionales son la de cocientes de enteros. Funciones racionales son funciones evaluadas en la forma de una fracción, donde el numerador y el denominador son polinomios. Estas expresiones racionales son el campo cociente de los polinomios (sobre algunos dominio de integridad).

La fracción continua es una expresión como 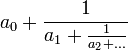$a_0 + \ frac {1} {a_1 + \ frac {1} {a_2 + ...}}$ , Donde el a _i son números enteros. Esto no es un elemento de un campo de cociente.

El término fracción parcial se utiliza en álgebra, cuando se descompone expresiones racionales (una fracción con una expresión algebraica en el denominador). El objetivo es escribir la expresión racional como la suma de otras expresiones racionales con denominadores de menor grado. 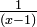Por ejemplo, la expresión racional $\ Estilo de texto {2x \ over (x ^ 2-1)}$ puede ser reescrita como la suma de dos fracciones: $\ Estilo de texto {1 \ over (x + 1)}$ y $\ Estilo de texto {1 \ over (x-1)}$ .

Herramientas pedagógicas

En escuelas primarias, las fracciones se han demostrado a través de Varillas Cuisenaire.

Los padres de niños fracciones de aprendizaje también deben ser conscientes de que la aritmética se enseña a menudo muy diferente con matemáticas de reforma. Muchos textos no dan la instrucción de los métodos estándar que pueden utilizar el mínimo común denominador, comparar o sumar fracciones. Algunos introducir conceptos de nuevo desarrollo como "tiras de fracciones" y fracciones de referencia (1/2, 1/4, 3/4 y 1/10), que no son familiares para los padres o matemáticos. Algunos están preocupados de que tales métodos no preparar a los estudiantes para las matemáticas en la universidad o la escuela secundaria. Si este es el caso, los padres pueden pedir a sus escuelas para complementar el aprendizaje de sus hijos con los métodos estándar o cambiar a los textos que dan la instrucción en los métodos tradicionales. Aritmética Fracción normalmente se enseña y se domina desde finales de la primaria a la escuela media. Sin embargo, algunos textos como las Matemáticas Connected no discuten la división de fracciones en todo incluso hasta el 8vo grado en CMP

Ver también los enlaces externos de abajo.

Historia

El primer uso conocido de fracciones decimales es ca. 2800 aC como antigua del valle del Indo unidades de medida . La Egipcios utilizaban fracciones egipcio ca. 1000 antes de Cristo. Los griegos utilizaron fracciones unitarias y posteriormente continuaron las fracciones y los seguidores del filósofo griego Pitágoras , ca. 530 aC, descubrió que el raíz cuadrada de dos no puede ser expresado como una fracción. En 150 aC Matemáticos Jain en la India escribió el "Sthananga Sutra", que contiene trabajos sobre la teoría de números, operaciones aritméticas, operaciones con fracciones .

Recuperado de " http://en.wikipedia.org/w/index.php?title=Fraction_(mathematics)&oldid=198200701 "