La mecánica estadística
Antecedentes
Esta selección wikipedia ha sido elegido por los voluntarios que ayudan Infantil SOS de Wikipedia para esta Selección Wikipedia para las escuelas. Ver http://www.soschildren.org/sponsor-a-child para averiguar sobre el apadrinamiento de niños.
| La mecánica estadística |
|---|
 |
|
Estadísticas de partículas
|
Conjuntos
|
Modelos
|
Potenciales
|
La mecánica estadística es la aplicación de la teoría de probabilidades , que incluye matemáticas herramientas para hacer frente a grandes poblaciones, con el campo de la mecánica, que tiene que ver con el movimiento de partículas u objetos cuando se somete a una fuerza. La mecánica estadística, a veces llamadas la física estadística, puede ser visto como un subcampo de la física y la química .
Proporciona un marco para relacionar las propiedades microscópicas de los átomos y moléculas individuales a las propiedades macroscópicas o granel de materiales que se pueden observar en la vida cotidiana, por lo tanto, que explica la termodinámica como un resultado natural de la estadística y la mecánica (clásica y cuántica) a nivel microscópico . En particular, se puede utilizar para calcular las propiedades termodinámicas de los materiales a granel a partir de los datos espectroscópicos de moléculas individuales.
Esta capacidad de hacer predicciones basadas en las propiedades macroscópicas microscópicas es la principal ventaja de la mecánica estadística más de la termodinámica . Ambas teorías se rigen por la segunda ley de la termodinámica a través del medio de la entropía . Sin embargo, la entropía en termodinámica sólo puede ser conocido empíricamente, mientras que en la mecánica estadística, es una función de la distribución del sistema en su micro-estados.
Postulado fundamental
El postulado fundamental de la mecánica estadística (también conocida como la igualdad de un postulado probabilidad a priori) es la siguiente:
- Dado un sistema aislado en equilibrio, se encuentra con la misma probabilidad en cada uno de sus accesible microestados.
Este postulado es una hipótesis fundamental en la mecánica estadística - que establece que un sistema en equilibrio no tiene ninguna preferencia por cualquiera de sus microestados disponibles. Dada microestados Ω a una energía particular, la probabilidad de encontrar el sistema en un microestado particular es p = 1 / Ω.
Este postulado es necesaria porque permite concluir que para un sistema en equilibrio, el estado termodinámico (macroestado) que podría resultar de un mayor número de microestados es también el macroestado más probable del sistema.
El postulado se justifica, en parte, por los sistemas clásicos, por El teorema de Liouville (hamiltoniano), que muestra que si el sistema de distribución de puntos a través accesible espacio de fase es uniforme en algún momento, sigue siendo así que en tiempos posteriores.
Justificación similar para un sistema discreto es proporcionada por el mecanismo de balance detallado.
Esto permite la definición de la función de información (en el contexto de teoría de la información):
Cuando todos rhos son iguales, I es mínima, lo que refleja el hecho de que tengamos una mínima información sobre el sistema. Cuando nuestra información es máxima, es decir, un rho es igual a uno y el resto a cero (ya sabemos en qué estado el sistema está en), la función es máxima.
Esta "función de la información" es la misma que la función entrópica reducida en termodinámica.
Colectividad microcanónica
En conjunto microcanónica N, V y E son fijos. Desde la segunda ley de la termodinámica se aplica a sistemas aislados, el primer caso investigado corresponderá a este caso. El conjunto microcanónica describe un sistema aislado.
La entropía de un sistema de este tipo sólo puede aumentar, de modo que el máximo de su entropía corresponde a una estado de equilibrio para el sistema.
Debido a que una aislado sistema mantiene una energía constante, el total de energía del sistema no fluctúa. Así, el sistema sólo puede acceder a los de sus micro-estados que corresponden a un valor E de la energía dada. La energía interna del sistema es entonces estrictamente igual a su energía .
Llamemos  el número de micro-estados correspondiente a este valor de la energía del sistema. El estado macroscópico de máxima entropía para el sistema es aquel en el que todos los micro-estados son igualmente probable que ocurra, con una probabilidad
el número de micro-estados correspondiente a este valor de la energía del sistema. El estado macroscópico de máxima entropía para el sistema es aquel en el que todos los micro-estados son igualmente probable que ocurra, con una probabilidad 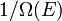 , Durante las fluctuaciones del sistema.
, Durante las fluctuaciones del sistema.
- donde
 es el sistema de entropía ,
es el sistema de entropía ,  es La constante de Boltzmann
es La constante de Boltzmann
Conjunto canónico
En conjunto canónico N, V y T son fijos. Invocando el concepto del conjunto canónico, es posible derivar la probabilidad  que un sistema macroscópico en equilibrio térmico con su entorno, será en un microestado dado con la energía
que un sistema macroscópico en equilibrio térmico con su entorno, será en un microestado dado con la energía 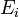 de acuerdo con la Distribución de Boltzmann:
de acuerdo con la Distribución de Boltzmann:
- donde
 ,
,
La temperatura 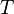 surge del hecho de que el sistema está en equilibrio térmico con su entorno. Las probabilidades de las diferentes microestados deben añadir a uno, y el factor de normalización en el denominador es la canónica función de partición:
surge del hecho de que el sistema está en equilibrio térmico con su entorno. Las probabilidades de las diferentes microestados deben añadir a uno, y el factor de normalización en el denominador es la canónica función de partición:
donde 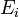 es la energía de la
es la energía de la  º microestado del sistema. La función de partición es una medida del número de estados accesibles al sistema a una temperatura dada. El artículo conjunto canónico contiene una derivación del factor de Boltzmann y la forma de la función de partición de los primeros principios.
º microestado del sistema. La función de partición es una medida del número de estados accesibles al sistema a una temperatura dada. El artículo conjunto canónico contiene una derivación del factor de Boltzmann y la forma de la función de partición de los primeros principios.
En resumen, la probabilidad de encontrar un sistema a temperatura 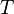 en un estado en particular con la energía
en un estado en particular con la energía 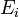 es
es
Conexión Termodinámica
La función de partición se puede utilizar para encontrar el (promedio) valor esperado de cualquier propiedad microscópica del sistema, que puede estar relacionado con variables macroscópicas. Por ejemplo, el valor esperado de la energía microscópica 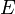 se interpreta como la definición microscópica de la energía interna variable termodinámica
se interpreta como la definición microscópica de la energía interna variable termodinámica  ., Y puede ser obtenido tomando la derivada de la función de partición con respecto a la temperatura. Ciertamente,
., Y puede ser obtenido tomando la derivada de la función de partición con respecto a la temperatura. Ciertamente,
implica, junto con la interpretación de 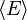 como
como  , La siguiente definición microscópica de energía interna:
, La siguiente definición microscópica de energía interna:
La entropía puede calcularse (véase La entropía de Shannon)
lo que implica que
es el energía libre del sistema o en otras palabras,
Tener expresiones microscópicas para los potenciales termodinámicos básicos  ( energía interna),
( energía interna),  ( entropía ) y
( entropía ) y 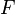 ( energía libre) es suficiente para derivar expresiones para otras magnitudes termodinámicas. La estrategia básica es como sigue. Puede haber una cantidad intensivo o extensivo que entra explícitamente en la expresión para la energía microscópica
( energía libre) es suficiente para derivar expresiones para otras magnitudes termodinámicas. La estrategia básica es como sigue. Puede haber una cantidad intensivo o extensivo que entra explícitamente en la expresión para la energía microscópica 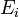 , Para el campo magnético ejemplo (intensivo) o el volumen (extensa). Entonces, las variables termodinámicas conjugadas son derivados de la energía interna. La magnetización macroscópica (extensa) es la derivada de
, Para el campo magnético ejemplo (intensivo) o el volumen (extensa). Entonces, las variables termodinámicas conjugadas son derivados de la energía interna. La magnetización macroscópica (extensa) es la derivada de  con respecto a la (intensivo) campo magnético, y la presión (intensivo) es la derivada de
con respecto a la (intensivo) campo magnético, y la presión (intensivo) es la derivada de  con respecto al volumen (extensa).
con respecto al volumen (extensa).
El tratamiento de esta sección no asume intercambio de materia (masa es decir, fija y el número de partículas fijas). Sin embargo, el volumen del sistema es variable lo que significa la densidad también es variable.
Esta probabilidad se puede utilizar para encontrar el valor medio, que corresponde al valor macroscópico, de cualquier propiedad, 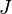 , Que depende del estado energético del sistema mediante el uso de la fórmula:
, Que depende del estado energético del sistema mediante el uso de la fórmula:
donde 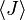 es el valor medio de la propiedad
es el valor medio de la propiedad  . Esta ecuación se puede aplicar a la energía interna,
. Esta ecuación se puede aplicar a la energía interna,  :
:
Posteriormente, estas ecuaciones se pueden combinar con las relaciones termodinámicas conocidas entre  y
y 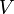 para llegar a una expresión para la presión en términos de sólo la temperatura, el volumen y la función de partición. Relaciones similares en términos de la función de partición se pueden derivar otras propiedades termodinámicas, como se muestra en la siguiente tabla; véase también la explicación detallada en configuración integral.
para llegar a una expresión para la presión en términos de sólo la temperatura, el volumen y la función de partición. Relaciones similares en términos de la función de partición se pueden derivar otras propiedades termodinámicas, como se muestra en la siguiente tabla; véase también la explicación detallada en configuración integral.
| Helmholtz energía libre: |  |
|---|---|
| Energía interna: |  |
| Presión: | 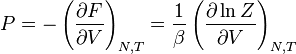 |
| Entropía : |  |
| Gibbs energía libre : |  |
| Entalpía : | 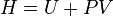 |
| Volumen constante capacidad calorífica: |  |
| Constante capacidad calorífica presión: |  |
| Potencial químico: |  |
Para aclarar, esto no es una conjunto canónico magnífico.
A menudo es útil considerar la energía de una molécula dada que se distribuye entre un número de modos. Por ejemplo, la energía de traslación se refiere a esa porción de la energía asociada con el movimiento del centro de masa de la molécula. Energía configuracional refiere a la porción de la energía asociada con las diversas fuerzas de atracción y repulsión entre las moléculas en un sistema. Los otros modos son todos considerados para ser interna a cada molécula. Incluyen modos rotacionales, vibracionales, electrónicos y nucleares. Si asumimos que cada modo es independiente (un supuesto cuestionable) la energía total se puede expresar como la suma de cada uno de los componentes:
Donde los subíndices  ,
,  ,
,  ,
,  ,
,  Y
Y  corresponden a la traducción, configuracional, nuclear, modos electrónicos, rotacionales y vibracionales, respectivamente. La relación en esta ecuación se puede sustituir en la primera ecuación para dar:
corresponden a la traducción, configuracional, nuclear, modos electrónicos, rotacionales y vibracionales, respectivamente. La relación en esta ecuación se puede sustituir en la primera ecuación para dar:
Si somos capaces de asumir todos estos modos son completamente desacoplado y no correlacionados, por lo que todos estos factores son en un sentido probabilidad totalmente independiente, entonces
Así, una función de partición se puede definir para cada modo. Las expresiones simples se han derivado en relación a cada uno de los distintos modos a diversas propiedades moleculares medibles, tales como las frecuencias de rotación o vibración característicos.
Las expresiones para las diversas funciones de partición molecular se muestran en la siguiente tabla.
| Nuclear |  |
|---|---|
| Electrónico |  |
| Vibracional | 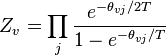 |
| Rotacional (lineal) | 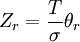 |
| Rotacional (no lineal) |  |
| Traslacional | 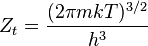 |
| Configuracional (gas ideal) |  |
Estas ecuaciones se pueden combinar con los de la primera tabla para determinar la contribución de un modo particular de la energía a una propiedad termodinámica. Por ejemplo, la "presión de rotación" se pudo determinar de esta manera. La presión total se pudo encontrar sumando las contribuciones de presión de todos los modos individuales, es decir:
Gran conjunto canónico
En gran canónica conjunto V, T y potencial químico son fijos. Si el sistema en estudio es un sistema abierto, (materia puede ser intercambiado), pero el número de partículas no se conserva, tendríamos que introducir potenciales químicos, μ j, j = 1, ..., n y reemplazar el canónica función de partición con el gran función de partición canónica:
donde N ij es el número de orden j partículas de especies en la i ª configuración. A veces, también tenemos otras variables a añadir a la función de partición, uno correspondiente a cada cantidad conservada. La mayoría de ellos, sin embargo, se puede interpretar de forma segura como potenciales químicos. En la mayoría de los sistemas de materia condensada, las cosas son no relativista y se conserva la masa. Sin embargo, la mayoría de los sistemas de materia condensada de interés también conservan el número de partículas de aproximadamente (metastably) y la masa (no relativista) es nada menos que la suma de la cantidad de cada tipo de partícula veces su masa. Masa está inversamente relacionada con la densidad, que es la variable conjugado a la presión. Para el resto de este artículo, vamos a ignorar esta complicación y pretender potenciales químicos no importan. Ver conjunto canónico magnífico.
Vamos a retrabajo todo utilizando un conjunto canónico magnífico este momento. El volumen se deja fijo y no figura en absoluto en este tratamiento. Como antes, j es el índice para aquellas partículas de especies j e i es el índice para microestado i:
| Gran potencial: |  |
| Energía interna: | 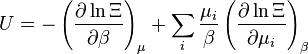 |
| Número de la partícula: |  |
| Entropía : |  |
| Helmholtz energía libre: | 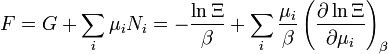 |
Equivalencia entre las descripciones en el límite termodinámico
Todas las descripciones anteriores se diferencian en la forma en que permiten que el sistema dado a fluctuar entre sus configuraciones.
En el micro-canónica conjunto, el sistema de intercambios sin energía con el mundo exterior, y por lo tanto no está sujeto a las fluctuaciones de energía, mientras que en el conjunto canónico, el sistema es libre de intercambiar energía con el exterior en forma de calor .
En el límite termodinámico, que es el límite de grandes sistemas, las fluctuaciones convertirse en insignificante, de modo que todas estas descripciones convergen a la misma descripción. En otras palabras, el comportamiento macroscópico de un sistema no depende de el conjunto particular utilizado para su descripción.
Dadas estas consideraciones, el mejor conjunto de elegir para el cálculo de las propiedades de un sistema macroscópico es ese conjunto que permite que el resultado se deriva más fácilmente.
Caminantes azar
El estudio de cadena larga polímeros ha sido una fuente de problemas dentro de los dominios de la mecánica estadística ya que alrededor del 1950. Una de las razones sin embargo que los científicos estaban interesados en su estudio es que las ecuaciones que rigen el comportamiento de una cadena de polímero fueron independientes de la química de la cadena. Lo que es más, la ecuación de gobierno resulta ser un paseo aleatorio (difusiva) en el espacio. De hecho, la ecuación de Schrödinger es en sí una ecuación de difusión en el tiempo imaginario,  .
.
Paseos aleatorios en el tiempo
El primer ejemplo de un paseo aleatorio es uno en el espacio, mediante el cual una partícula se somete a un movimiento aleatorio debido a fuerzas externas en su medio circundante. Un ejemplo típico sería un grano de polen en un vaso de precipitados de agua. Si uno pudiera de alguna manera "teñir" el camino del grano de polen ha tomado, la trayectoria observada se define como un paseo aleatorio.
Considere un problema juguete, de un tren que se mueve a lo largo de una pista de 1D en la dirección x. Supongamos que el tren se mueve ya sea una distancia de + o - una distancia b fija, en función de si una moneda cae cara o cruz cuando volteado. Vamos a empezar por considerar las estadísticas de los pasos que el tren de juguete lleva (donde  es el paso ITH tomado):
es el paso ITH tomado):
 ; debido a priori probabilidades iguales
; debido a priori probabilidades iguales 
La segunda cantidad se conoce como el función de correlación. El delta es el delta de Kronecker que nos dice que si los índices iyj son diferentes, entonces el resultado es 0, pero si i = j, entonces el delta de Kronecker es 1, por lo que la función de correlación devuelve un valor de  . Esto tiene sentido, porque si i = j entonces estamos considerando el mismo paso. Más bien trivialmente entonces se puede demostrar que el desplazamiento promedio del tren en el eje x es 0;
. Esto tiene sentido, porque si i = j entonces estamos considerando el mismo paso. Más bien trivialmente entonces se puede demostrar que el desplazamiento promedio del tren en el eje x es 0;



Como se ha indicado 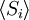 es 0, por lo que la suma de 0 todavía es 0. También se puede demostrar, usando el mismo método ha demostrado anteriormente, para calcular el valor cuadrático medio de problema. El resultado de este cálculo se da a continuación
es 0, por lo que la suma de 0 todavía es 0. También se puede demostrar, usando el mismo método ha demostrado anteriormente, para calcular el valor cuadrático medio de problema. El resultado de este cálculo se da a continuación
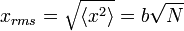
Desde el ecuación de difusión se puede demostrar que la distancia una partícula de difusión se mueve en un medio es proporcional a la raíz del tiempo que el sistema ha sido de difusión del, donde la constante de proporcionalidad es la raíz de la constante de difusión. La relación anterior, aunque de aspecto diferente, revela la física similares, donde N es simplemente el número de pasos movidos (está vagamente conectados con el tiempo) y b es la longitud del paso característico. Como consecuencia, podemos considerar la difusión como un proceso de paseo aleatorio.
Camina al azar en el espacio
Camina al azar en el espacio puede ser pensado como instantáneas del camino tomado por un caminante al azar en el tiempo. Un ejemplo es la configuración espacial de polímeros de cadena larga.
Hay dos tipos de caminata aleatoria en el espacio: auto evitando paseos aleatorios, donde los eslabones de la cadena de polímero interactúan y no se solapan en el espacio, y los paseos aleatorios puros, donde los eslabones de la cadena de polímero no son interactuantes y los enlaces son libres de estar uno encima del otro. El primer tipo es más aplicable a los sistemas físicos, pero sus soluciones son más difíciles de conseguir en a partir de primeros principios.
Al considerar una cadena de polímero libremente articulado que no interactúan, el vector de extremo a extremo es 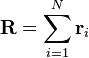 donde
donde 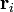 es el vector de posición del enlace i-ésimo en la cadena. Como resultado de la teorema del límite central, si N >> 1 entonces la esperamos una distribución gaussiana para el vector de extremo a extremo. También podemos hacer declaraciones de las estadísticas de los propios enlaces;
es el vector de posición del enlace i-ésimo en la cadena. Como resultado de la teorema del límite central, si N >> 1 entonces la esperamos una distribución gaussiana para el vector de extremo a extremo. También podemos hacer declaraciones de las estadísticas de los propios enlaces; 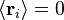 ; por la isotropía del espacio
; por la isotropía del espacio 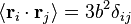 ; todos los eslabones de la cadena no están correlacionados entre sí
; todos los eslabones de la cadena no están correlacionados entre sí
Utilizando las estadísticas de los enlaces individuales, se demuestra fácilmente que  y
y 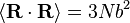 . Observe este último resultado es el mismo que se encuentra de paseo al azar en el tiempo.
. Observe este último resultado es el mismo que se encuentra de paseo al azar en el tiempo.
Suponiendo, como se ha dicho, que esa distribución de los vectores de extremo a extremo para un gran número de cadenas de polímeros idénticos es gaussiana, la distribución de probabilidad tiene la siguiente forma

¿Para qué sirve esto? Recordemos que de acuerdo con el principio de igual probabilidad probabilidades a priori, el número de microestados, Ω, en algún valor físico es directamente proporcional a la distribución de probabilidad en ese valor físico, a saber;

donde c es una constante de proporcionalidad arbitraria. Dada nuestra función de distribución, hay una maxima correspondiente a  . Físicamente esto equivale a que hay más microestados que tienen un vector de 0 que cualquier otro microestado de extremo a extremo. Ahora, considerando
. Físicamente esto equivale a que hay más microestados que tienen un vector de 0 que cualquier otro microestado de extremo a extremo. Ahora, considerando 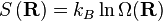


donde F es la Energía libre de Helmholtz es trivial demostrar que 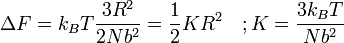
Un resorte Hookian!
Este resultado se conoce como la Primavera Entropic Resultado y equivale a decir que al estirar una cadena de polímero que está haciendo trabajo en el sistema de arrastrarlo lejos de su (preferido) estado de equilibrio. Un ejemplo de esto es una banda elástica común, compuesto de polímeros de cadena larga (de goma). Al estirar la banda elástica que está haciendo trabajos en la instalación y la banda se comporta como un resorte convencional. Lo que es particularmente sorprendente de este resultado sin embargo, es que el trabajo realizado en el estiramiento de la cadena de polímero puede estar relacionado enteramente a la variación de entropía del sistema como resultado de el estiramiento.
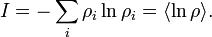
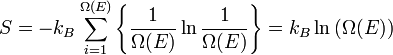

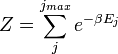

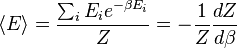

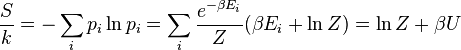
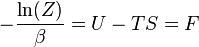


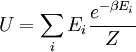

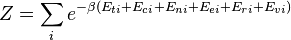


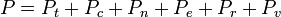
![\ Xi (V, T, \ mu) = \ sum_i \ exp \ left (\ beta \ left [\ sum_ {j = 1} ^ n \ mu_j N_ {ij} -E_i \ right] \ right)](../../images/633/63360.png)