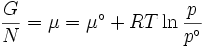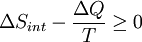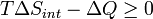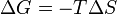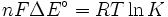Energía libre de Gibbs

Temas relacionados: Química

Acerca de este escuelas selección Wikipedia

SOS Children produjo este sitio web para las escuelas, así como este sitio web video sobre África . SOS Children ha cuidado de niños en África durante cuarenta años. ¿Puedes ayudar a su trabajo en África ?

La mecánica estadística

Termodinámica Teoría cinética
Estadísticas de partículas Spin-Estadísticas Teorema Partículas idénticas Maxwell-Boltzmann Bose-Einstein Fermi-Dirac Parastatistics Estadísticas Anyonic Estadísticas Braid
Conjuntos Microcanónica Canónico Gran canónica Isotérmico isobárica -Isentálpica isobárica Abrir estadística
Modelos Debye Einstein Yo Canto
Potenciales Energía interna Entalpía Energía libre de Helmholtz Energía libre de Gibbs Gran potencial / Landau energía libre
Los científicos Maxwell Gibbs Boltzmann Einstein Debye Fermi

En termodinámica , la energía libre de Gibbs ( IUPAC nombre recomendado: energía de Gibbs o función de Gibbs) es un potencial termodinámico que mide el "útil" o proceso de iniciar un trabajo que se puede obtener a partir de un isotérmica, isobárica sistema termodinámico. Técnicamente, la energía libre de Gibbs es la máxima cantidad de trabajo no-expansión que se puede extraer de un sistema cerrado o este máximo sólo puede alcanzarse de forma totalmente proceso reversible. Cuando un sistema pasa de un estado inicial bien definido a un estado final bien definido, el Gibbs energía libre? G es igual al trabajo intercambiado por el sistema con su entorno, menos el trabajo de las fuerzas de presión, durante una transformación reversible del sistema del mismo estado inicial al mismo estado final.

Energía de Gibbs es también el potencial químico que se minimiza cuando un sistema alcanza el equilibrio a la presión y temperatura constantes. Como tal, es un criterio de espontaneidad conveniente para procesos con presión y temperatura constante.

La energía libre de Gibbs, originalmente llamada energía disponible, se desarrolló en la década de 1870 por el físico matemático estadounidense Willard Gibbs . En 1873, en una nota al pie, Gibbs define lo que él llamó la "energía disponible" de un cuerpo como tal:

La mayor cantidad de trabajo mecánico que se puede obtener a partir de una determinada cantidad de una determinada sustancia en un estado inicial dado, sin aumentar su total de volumen o permitir que el calor pase o de órganos externos, excepto los que al cierre de los procesos son dejado en su condición inicial.

El estado inicial del cuerpo, de acuerdo con Gibbs, se supone que es tal que "el cuerpo puede hacerse pasar de ella a los estados de energía disipada por procesos reversibles ". En su 1876 obra maestra En el equilibrio de sustancias heterogéneas, un análisis gráfico de sistemas químicos de varias fases, que dedica sus pensamientos sobre la energía libre de químicos en su totalidad.

Definiciones

Willard Gibbs 1873 energía disponible (energía libre) gráfico ', que muestra un plano perpendicular al eje de v ( volumen ) y pasa por el punto A, que representa el estado inicial del cuerpo. MN es la sección de la superficie de energía disipada. Qε y Qη son secciones de los planos η = 0 y ε = 0, y por lo tanto paralelos a los ejes de ε ( energía interna) y η ( entropía ), respectivamente. AD y AE son la energía y la entropía del cuerpo en su estado inicial, AB y AC su energía disponible (la energía libre de Gibbs) y su capacidad de entropía (la cantidad en que la entropía del cuerpo se puede aumentar sin cambiar la energía de el cuerpo o el aumento de su volumen), respectivamente.

La energía libre de Gibbs se define como:

$G = U + pV-TS \,$

que es el mismo que:

$G = H-TS \,$

donde:

U es la energía interna ( Unidad SI: Joule)
p es presión (unidad SI: pascal)
V es el volumen (Unidad SI: m ³⁾
T es la temperatura (unidad SI: kelvin )
S es la entropía (unidad SI: joule por kelvin)
H es la entalpía (unidad SI: julios)

La expresión para el cambio reversible infinitesimal en la energía libre de Gibbs, para una sistema abierto, sometido a la operación de fuerzas externas X _i, que causan los parámetros externos del sistema a _i a cambio por una cantidad _i da, viene dada por:

$\ Mathrm {d} G = V \ mathrm {d} pS \ mathrm {d} t + \ sum_ {i = 1} ^ k \ mu_i \, \ mathrm {d} N_i + \ sum_ {i = 1} ^ n X_i \, \ mathrm {d} a_i + \ ldots \,$

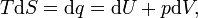$T \ mathrm {d} S = \ mathrm {d} q = \ mathrm {d} U + p \ mathrm {d} V,$ donde:

$\ Mu_i$ es el potencial químico del -ésimo i componente químico. (Unidad SI: julios por partículas o julios por mol)
$N_i$ es el número de partículas (o número de moles) que componen componente químico el i-ésimo.

Esta es una forma de Gibbs ecuación fundamental. En la expresión infinitesimal, el plazo, que incluye las cuentas potenciales químicos de los cambios en la energía libre de Gibbs resultantes de una afluencia o outflux de partículas. En otras palabras, que tiene para una sistema abierto. Para sistema cerrado, este término se puede eliminar.

Cualquier número de términos adicionales se puede añadir, dependiendo del sistema particular que está siendo considerado. Aparte de trabajo mecánico , un sistema puede además realizar numerosos otros tipos de trabajo. Por ejemplo, en la expresión infinitesimal, la energía de trabajo contráctil asociada con un sistema termodinámico que es una fibra contráctil que acorta por una cantidad - dl bajo una fuerza f daría lugar a que se añade una fdl plazo. Si una cantidad de carga - de es adquirida por un sistema en una Ψ potencial eléctrico, el trabajo eléctrico asociado con esto es -Ψ de, que se incluye en la expresión infinitesimal. Otros términos de trabajo se añaden por los requisitos del sistema.

Cada cantidad en las ecuaciones anteriores se puede dividir por la cantidad de sustancia, medido en lunares, para formar molar energía libre de Gibbs. La energía libre de Gibbs es una de las funciones termodinámicas más importantes para la caracterización de un sistema. Es un factor en los resultados determinantes tales como la voltaje de una celda electroquímica, y el constante de equilibrio para una reacción reversible. En isotérmica, los sistemas de isobáricas, energía libre de Gibbs puede ser pensado como una cantidad "dinámica", en que es una medida representativa de los efectos de las fuerzas que compiten entálpicos y de conducción entrópico que participan en un proceso termodinámico.

La dependencia de la temperatura de la energía de Gibbs para un gas ideal está dada por la Gibbs-Helmholtz ecuación y su dependencia de la presión viene dada por:

$\ Frac {G} {N} = \ frac {G} {N} ^ \ circ + kT \ ln \ frac {p} {{p ^ \ circ}}$

si el volumen es conocido en lugar de la presión entonces se convierte en:

$\ Frac {G} {N} = \ frac {G} {N} ^ \ circ + kT \ ln \ frac {V ^ \ circ} {{V}}$

o más convenientemente como su potencial químico:

$\ Frac {G} {N} = \ mu = \ mu ^ \ circ + RT \ ln \ frac {p} {{p ^ \ circ}}$

En los sistemas no ideales, fugacidad entra en juego.

Derivación

La energía libre de Gibbs diferencial total en términos de su variables naturales pueden derivarse a través de Legendre transforma de la energía interna. Para un sistema de someterse a un proceso internamente reversible que se le permite intercambiar materia, calor y trabajo con su entorno, el diferencial de la energía interna se da desde la primera ley de la termodinámica como

$\ Mathrm {d} T = T \ mathrm {d} S - p \, \ mathrm {d} V + \ sum_i \ mu_i \, \ mathrm {d} N_i \,$ .

Porque $S$ , $V$ Y $\ {N_i \}$ son las variables extensivas, Función homogénea teorema de Euler permite una fácil integración de $\ Mathrm {d} U$ :

$T = T S - p V + \ sum_i \ mu_i N_i \,$ .

La definición de $G$ desde arriba es

$G = U + p V - T S \,$ .

Tomando la diferencial total, tenemos

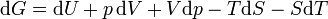$\ Mathrm {d} G = \ mathrm {d} U + p \, \ mathrm {d} V + V \ mathrm {d} p - T \ mathrm {d} S - S \ mathrm {d} T \,$ .

Sustitución $\ Mathrm {d} U$ con el resultado de da la primera ley

$\ Mathrm {d} G = T \ mathrm {d} S - p \, \ mathrm {d} V + \ sum_i \ mu_i \, \ mathrm {d} N_i + p \, \ mathrm {d} V + V \ mathrm {d} p - T \ mathrm {d} S - S \ mathrm {d} T \,$

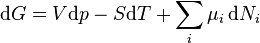$\ Mathrm {d} G = V \ mathrm {d} p - S \ mathrm {d} t + \ sum_i \ mu_i \, \ mathrm {d} N_i \,$ .

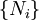Las variables naturales de $G$ son entonces $p$ , $T$ Y $\ Left \ {N_i \ right \}$ . Debido a que algunas de las variables naturales son intensivos, $d G$ no pueden estar integradas utilizando integrales de Euler como es el caso con la energía interna. Sin embargo, simplemente sustituyendo el resultado de $U$ en la definición de $G$ da una expresión estándar para G:

$G = T S - p V + \ sum_i \ mu_i N_i + p V - T S \,$

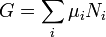$G = \ sum_i \ mu_i N_i \,$ .

Visión de conjunto

De una manera simple, con respecto a las STP sistemas reaccionar, un general regla de oro es:

Cada sistema trata de alcanzar un mínimo de energía libre.

Por lo tanto, fuera de esta tendencia natural en general, una medida cuantitativa en cuanto a cómo cerca o lejos una reacción potencial es de este mínimo es cuando la energética calculados del proceso indican que el cambio en la energía libre de Gibbs? G es negativo. Esencialmente, esto significa que tal reacción se verá favorecida y liberar energía. La energía liberada es igual a la cantidad máxima de trabajo que puede ser realizado como resultado de la reacción química. A la inversa, si las condiciones indican un Delta G positiva, entonces la energía - en la forma de trabajo - tendría que ser añadido al sistema de reacción para hacer la reacción ir.

Historia

La cantidad llamada "energía libre" es esencialmente un reemplazo más avanzada y precisa para el término anticuado " afinidad ", que fue utilizado por los químicos en años anteriores para describir la" fuerza "que causó reacciones químicas . La afinidad plazo, tal como se utiliza en relación química, se remonta al menos a la hora de Alberto Magno en 1250.

De los 1998 libros de texto modernos Termodinámica por el premio Nobel y profesor de ingeniería química Ilya Prigogine encontramos:?? "A medida que el movimiento se explica por el concepto newtoniano de fuerza, los químicos querían un concepto similar de 'motor' para el cambio químico ¿Por qué ocurren las reacciones químicas, y por qué hacer que se detengan en ciertos puntos Químicos llamado el ' fuerza 'que causó afinidad reacciones químicas, pero carecía de una definición clara ".

Durante todo el siglo 18, la opinión dominante en cuanto al calor y la luz era la formulada por Isaac Newton , llamada la "hipótesis de Newton", que afirmaron que la luz y el calor son formas de la materia atraídos o repelidos por otras formas de la materia, con fuerzas análogas a la gravitación o la afinidad química.

En el siglo 19, el químico francés Marcelino Berthelot y el químico danés Julius Thomsen había intentado cuantificar afinidad utilizando calores de reacción. En 1875, después de la cuantificación de los calores de reacción para un gran número de compuestos, Berthelot propuso la " principio de trabajo máximo "en el que todos los cambios químicos que ocurren sin la intervención de la energía exterior tienden hacia la producción de cuerpos o de un sistema de cuerpos que liberan calor .

Además de esto, en 1780 Antoine Lavoisier y Pierre-Simon Laplace sentaron las bases de termoquímica mostrando que el calor dada a cabo en una reacción es igual al calor absorbido en la reacción inversa. También investigaron la calor específico y calor latente de un número de sustancias, y cantidades de calor propuestos en la combustión. Del mismo modo, en 1840 el químico suizo Germain Hess formuló el principio de que la evolución de calor en una reacción es la misma si el proceso se realiza en un solo paso o en un número de etapas. Esto se conoce como La ley de Hess. Con el advenimiento de la teoría mecánica del calor en el siglo 19, la ley de Hess llegó a ser visto como una consecuencia de la ley de conservacion de energia.

Sobre la base de estas y otras ideas, Berthelot y Thomsen, así como otros, considerado el calor emitido en la formación de un compuesto como una medida de la afinidad, o el trabajo realizado por las fuerzas químicas. Este punto de vista, sin embargo, no era del todo correcto. En 1847, el físico Inglés James Joule demostró que podía elevar la temperatura del agua girando una rueda de paletas en ella, mostrando de esta manera que el calor y trabajo mecánico fueron equivalentes o proporcionales entre sí, es decir, aproximadamente, $dW \ propto dQ$ . Esta declaración vino a ser conocido como el equivalente mecánico del calor y era una forma precursora de la primera ley de la termodinámica .

En 1865 el físico alemán Rudolf Clausius había demostrado que este principio de equivalencia necesaria enmienda. Es decir, uno puede utilizar el calor derivado de una reacción de combustión en un horno de carbón para hervir el agua, y utilizar este calor para evaporar el vapor, y luego usar la energía de alta presión mejorada del vapor vaporizado para empujar un pistón. Así, podríamos razonar ingenuamente que uno puede convertir completamente el calor de combustión inicial de la reacción química en el trabajo de empujar el pistón. Clausius mostró, sin embargo, que tenemos que tener en cuenta la labor que las moléculas del cuerpo de trabajo, es decir, las moléculas de agua en el cilindro, hacer el uno del otro a medida que pasan o transformar de un paso o estado de la ciclo del motor a la siguiente, por ejemplo, a partir de (P1, V1) a (P2, V2). Clausius originalmente llamó a esto el "contenido transformación" del cuerpo, y más tarde cambió el nombre a la entropía . Por lo tanto, el calor usado para transformar el cuerpo de trabajo de las moléculas de un estado al siguiente no se puede utilizar para hacer el trabajo externo, por ejemplo, para empujar el pistón. Clausius definió este calor transformación como dQ = TdS.

En 1873, Willard Gibbs publicó un método de representación geométrica de las propiedades termodinámicas de las sustancias por medio de superficies en la que introdujo el esquema preliminar de los principios de su nueva ecuación capaces de predecir o estimar las tendencias de varios procesos naturales que sobrevendrá cuando los cuerpos o sistemas se ponen en contacto. Mediante el estudio de las interacciones de sustancias homogéneas en contacto, es decir, órganos, siendo en la composición de parte sólida, parte líquida y parte vapor, y mediante el uso de un tridimensional volumen - entropía - gráfico interior de la energía, Gibbs fue capaz de determinar tres estados de equilibrio, es decir, "necesariamente estable", "neutral", y "inestable", y si o no los cambios se producirán. En 1876, Gibbs construido en este marco mediante la introducción del concepto de potencial químico de manera que tome en cuenta las reacciones químicas y los estados de los órganos que son químicamente diferentes entre sí. En sus propias palabras, para resumir sus resultados en 1873, Gibbs dice:

En esta descripción, tal como se utiliza por Gibbs, ε se refiere a la energía interna del cuerpo, η se refiere a la entropía del cuerpo, y ν es el volumen del cuerpo.

Por lo tanto, en 1882, después de la introducción de estos argumentos por Clausius y Gibbs, el científico alemán Hermann von Helmholtz declaró, en oposición a Berthelot y Thomas 'hipótesis de que la afinidad química es una medida del calor de reacción de la reacción química como basado en el principio de máxima de trabajo, que la afinidad no es el calor emitido en la formación de un compuesto sino que es la mayor cantidad de trabajo que se puede obtener cuando la reacción se lleva a cabo de una manera reversible, por ejemplo, el trabajo eléctrico en una célula reversible. El trabajo máxima es así considerada como la disminución de los libres, o disponibles, la energía del sistema (energía libre de Gibbs G a T = constante, P = constante o energía libre de Helmholtz F a T = constante, V = constante), mientras que el calor emitido a cabo por lo general es una medida de la disminución de la energía total del sistema ( Energía interna). Por lo tanto, G o F es la cantidad de energía "libre" para el trabajo en las condiciones dadas.

Hasta este punto, la vista general había sido tal que: "todas las reacciones químicas conducen al sistema a un estado de equilibrio en el que las afinidades de las reacciones desaparecen". Durante los próximos 60 años, la afinidad término llegó a ser reemplazado por la libre expresión de la energía. Según el historiador química Henry Leicester, el influyente libro de texto de 1923 Termodinámica y la energía libre de las reacciones químicas por Gilbert N. Lewis y Merle Randall llevó a la sustitución del término "afinidad" por el término "energía libre" en gran parte del mundo de habla Inglés.

¿Qué significa el término "libre"?

En los siglos 18 y 19, la teoría del calor, es decir, que el calor es una forma de energía que tiene relación con movimiento vibratorio, empezaba a suplantar tanto la teoría calórica, es decir, que el calor es un fluido, y el cuatro teoría elemento en el que el calor era el más ligero de los cuatro elementos. Muchos libros de texto y artículos de enseñanza durante estos siglos presentan estas teorías al lado del otro. Del mismo modo, durante estos años, el calor empezaba a distinguirse en diferentes categorías de clasificación, como "calor libre", "producción combinada de calor", "calor radiante", calor especifico, capacidad calorífica, "calor absoluto", "calórico latente", "libre" o "perceptible" calórica (calorique sensible), entre otros.

En 1780, por ejemplo, Laplace y Lavoisier declararon: "En general, se puede cambiar la primera hipótesis en el segundo, cambiando las palabras" sin calor combinada de calor, y el calor liberado "en" . vis viva, pérdida de fuerza viva, y aumento de la fuerza viva '"De esta manera, la masa total de calorías en un cuerpo, llamado calor absoluta, fue considerada como una mezcla de dos componentes; el calórico libre o perceptible podría afectar un termómetro mientras que el otro componente, el calórico latente, no podía. El uso de las palabras "calor latente" implicaba una similitud con el calor latente en el sentido más habitual; se consideraba ligado químicamente a las moléculas del cuerpo. En el adiabático compresión de un gas el calor absoluta se mantuvo constante por el aumento observado de la temperatura, lo que indica que algunos calórico latente se había convertido en "libre" o perceptible.

Durante el siglo 19, el concepto de calorías perceptible o libre comenzó a ser conocido como "el calor libre" o el calor liberado. En 1824, por ejemplo, el físico francés Sadi Carnot, en sus famosas "Reflexiones sobre la potencia motriz del fuego", habla de cantidades de calor 'absorbidos o puestos en libertad' en diferentes transformaciones. En 1882, el físico y fisiólogo alemán Hermann von Helmholtz acuñó la frase 'energía libre' para la expresión E - TS, en la que el cambio de F (o G) determina la cantidad de energía "libre" para el trabajo en las condiciones dadas.

Así, en el uso tradicional, el término "libre" se adjuntó a energía libre de Gibbs, es decir, para sistemas a presión y temperatura constante, o para energía libre de Helmholtz, es decir, para sistemas en volumen y temperatura constante, para significar "disponible en la forma de trabajo útil ". Con referencia a la energía libre de Gibbs, añadimos la calificación que es la energía libre para el trabajo no volumen.

Un creciente número de libros y artículos de revistas no incluyen el archivo adjunto "libre", en referencia a G como simplemente energía de Gibbs (y lo mismo para el La energía de Helmholtz). Este es el resultado de un 1,988 Reunión de la IUPAC para establecer terminologías unificadas para la comunidad científica internacional, en la que supuestamente fue desterrado el adjetivo "libre". Esta norma, sin embargo, aún no se ha adoptado universalmente, y muchos artículos y libros publicados todavía incluyen el descriptivo "libre".

La energía libre de las reacciones

Para derivar la ecuación de la energía libre de Gibbs para un aislado sistema, sea S _tot ser la entropía total del sistema aislado, es decir, un sistema que no puede intercambiar calor o masa con su entorno. De acuerdo con la segunda ley de la termodinámica :

$\ Delta S_ {tot} \ GE 0 \,$

y si $\ Delta S_ {tot} = 0 \,$ entonces el proceso es reversible. La transferencia de calor $\ Delta Q$ desaparece para un sistema adiabático. Cualquier proceso adiabático que también es reversible se llama isentrópico 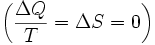$\ Left ({\ Delta Q \ over T} = Delta S = 0 \ right \) \,$ proceso.

Ahora considere sistemas diabáticos, teniendo entropía S interna _int. Dicho sistema está conectado térmicamente con su entorno, que tienen entropía S _ext. La forma de la entropía de la segunda ley no se aplica directamente al sistema diabático, sólo se aplica al sistema cerrado formado por el sistema y su entorno. Por lo tanto un proceso es posible si

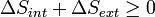$\ Delta S_ {int} + \ Delta S_ {ext} \ GE 0 \,$ .

Vamos a tratar de expresar el lado izquierdo de esta ecuación enteramente en términos de las funciones del Estado? S _ext se define como.:

$\ Delta S_ {ext} = - {\ Delta Q \ over T} \,$

Temperatura T es la misma para dos sistemas en equilibrio térmico. Por el ley cero de la termodinámica, si un sistema está en equilibrio térmico con un segundo y un tercer sistema, estos dos últimos están en equilibrio también. También, $\ Delta Q$ es el calor transferido al sistema, por lo $- \ Delta Q$ es el calor transferido a los alrededores, y -ΔQ / T es la entropía ganado por los alrededores. Ahora tenemos:

$\ Delta S_ {int} - {\ Delta Q \ over T} \ GE 0 \,$

Multiplique ambos lados por T:

$T \ Delta S_ {int} - \ Delta Q \ GE 0 \,$

ΔQ es el calor transferido al sistema; si el proceso se supone que es ahora isobárica, entonces ΔQ _p =? H:

$T \ Delta S_ {int} - \ Delta H \ GE 0 \,$

? H es el cambio de entalpía de la reacción (para una reacción química a presión constante y temperatura). Entonces

$\ Delta H - T \ Delta S_ {int} \ le 0 \,$

para un posible proceso. Deje que el cambio Δ G en energía libre de Gibbs se define como

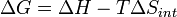$\ Delta G = \ Delta H - T \ Delta S_ {int} \,$ (Eq.1)

Observe que no se define en términos de las funciones estatales externos, como Δ S _ext o Δ S _tot. Luego la segunda ley se convierte, que también nos habla de la espontaneidad de la reacción:

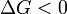$\ Delta G <0 \,$ reacción favorecida (espontánea)

$\ Delta G = 0 \,$ Ni el delantero ni la reacción inversa prevalece ( Equilibrium )

$\ Delta G> 0 \,$ reacción desfavorecida (no espontánea)

Energía libre de Gibbs G en sí se define como

$G = H - T S_ {int} \,$ (Ecuación 2)

Pero Tenga en cuenta que para obtener la ecuación (2) de la ecuación (1) debemos suponer que T es constante. Por lo tanto, energía libre de Gibbs es más útil para los procesos termoquímicos a temperatura y presión constantes: tanto isotérmico y isobárica. Tales procesos no se mueven en un P - T diagrama, tales como cambio de fase de una sustancia pura, que tiene lugar a la presión de saturación y la temperatura. Las reacciones químicas, sin embargo, no sufren cambios en potencial químico, que es una función de estado. Por lo tanto, los procesos termodinámicos no se limitan a las dos dimensiones P - diagrama V. Hay una tercera dimensión para n, la cantidad de gas. Naturalmente para el estudio de los productos químicos explosivos, los procesos no son necesariamente isotérmica y isobárica. Para estos estudios, Se utiliza la energía libre de Helmholtz.

Si un sistema cerrado (Δ Q = 0) es a presión constante (Δ Δ Q = H), entonces

$\ Delta H = 0 \,$

Por lo tanto la energía libre de Gibbs de un sistema cerrado es:

$\ Delta G = -T \ Delta S \,$

y si $\ Delta G \ le 0 \,$ a continuación, esto implica que 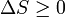$\ Delta S \ GE 0 \,$ , De vuelta al punto de partida la derivación de Δ G.

Identidades útiles

$\ Delta G = \ Delta H - T \ Delta S \,$ para temperatura constante

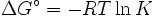
$\ Delta G ^ \ circ = -R T \ ln K \,$

$\ Delta G = \ Delta G ^ \ circ + R T \ ln Q \,$

$\ Delta G = -nf \ Delta E \,$

y reordenando da

$nF \ Delta E ^ \ circ = RT \ ln K \,$

$nF \ Delta E = nF \ Delta E ^ \ circ - R T \ ln Q \, \,$

$\ Delta E = \ Delta E ^ \ circ - \ frac {RT} {n} F \ ln Q \, \,$

que relaciona el potencial eléctrico de una reacción con el coeficiente de equilibrio para esta reacción.

donde

Δ G = cambio en la energía libre de Gibbs, Δ H = cambio de entalpía , T = absoluto de temperatura , Δ S = cambio en la entropía , R = constante de los gases, ln = logaritmo natural , K = constante de equilibrio, Q = cociente de reacción, n = número de electrones por producto en moles, F = Constante de Faraday ( culombios por mol), y Δ E = potencial eléctrico de la reacción. Por otra parte, también tenemos:

$K_ {eq} = e ^ {- \ frac {\ Delta G ^ \ circ} {RT}}$

$\ Delta G ^ \ circ = -RT (\ ln K_ {eq}) = -2.303RT (\ log K_ {eq})$

que relaciona la constante de equilibrio con la energía libre de Gibbs.

Cambio estándar de formación

La energía libre de Gibbs estándar de formación de un compuesto es el cambio de energía libre de Gibbs que acompaña la formación de 1 mol de dicha sustancia a partir de sus elementos componentes, en su estados estándar (la forma más estable del elemento a 25 grados Celsius y 100 kilopascales). Su símbolo es Δ G _f ~~^S.~~

Todos los elementos en sus estados estándar ( oxígeno gas, grafito, etc.) tienen 0 estándar Gibbs cambio de energía libre de formación, ya que no hay cambio en cuestión.

Δ G = Δ G ˚ + RT ln Q

En el equilibrio, Δ G = 0 y Q = K por lo que la ecuación se convierte en Δ G ˚ = - RT ln K

Tabla de sustancias seleccionadas

Sustancia	Estado	Δ G ˚ ( cal / mol)
NH ₃	g	-3.976
H ₂ O	lq	-56.69
H ₂ O	g	-54.64
CO ₂	g	-94.26
Colorado	g	-32.81
CH ₄	g	-12.14
C ₂ H ₆	g	-7.86
C ₃ H ₈	g	-5.614
C ₈ H ₁₈	g	4.14
C ₁₀ H ₂₂	g	8.23

Recuperado de " http://en.wikipedia.org/w/index.php?title=Gibbs_free_energy&oldid=198020586 "

See also ebooksgratis.com: no banners, no cookies, totally FREE.