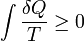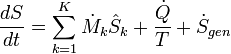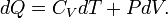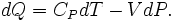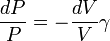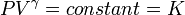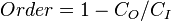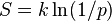Entropía
Antecedentes de las escuelas de Wikipedia
SOS ofrecen una descarga completa de esta selección de escuelas para su uso en escuelas intranets. Todos los niños disponibles para el apadrinamiento de niños de Aldeas Infantiles SOS son atendidos en una casa de familia por la caridad. Leer más ...

| Artículos Entropy |
|---|
| Introducción |
| Historia |
| Clásico |
| Estadístico |
En la termodinámica (una rama de la física ), la entropía es una medida de la falta de disponibilidad de un del sistema de energía para hacer el trabajo .
Es una medida de la aleatoriedad de las moléculas en un sistema y es central para la segunda ley de la termodinámica y de la ley combinada de la termodinámica, que se ocupan de los procesos físicos y si se producen de forma espontánea. Cambios espontáneos, en sistemas aislados, se producen con un aumento en la entropía. Cambios espontáneos tienden a suavizar las diferencias de temperatura , la presión, la densidad , y potencial químico que pueda existir en un sistema, y la entropía es, pues, una medida de hasta qué punto este proceso de suavizado de salida ha progresado.
La palabra "entropía" se deriva del griego εντροπία "un giro hacia" (εν- "en" + τροπή "un giro"), y es simbolizado por S en la física.
Explicación
Cuando la energía de un sistema se define como la suma de su energía "útil", (por ejemplo, que se utiliza para empujar un pistón), y su "energía inútil", es decir, que la energía que no se puede utilizar para el trabajo externo , entonces la entropía puede ser (la mayoría concretamente) visualizado como la "chatarra" o energía "inútil", cuya prevalencia enérgico sobre la energía total de un sistema es directamente proporcional a la temperatura absoluta del considerado sistema. (Tenga en cuenta los "TS" de productos en la energía libre de Gibbs o Las relaciones de energía libre de Helmholtz).
La entropía es una función de una cantidad de calor que muestra la posibilidad de conversión de ese calor en trabajo. El aumento en la entropía es pequeña cuando se añade calor a alta temperatura y es mayor cuando se añade calor a temperatura más baja. Así, por máxima entropía hay disponibilidad mínima para la conversión en el trabajo y para la entropía mínima existe la máxima disponibilidad para su conversión en el trabajo.
Cuantitativamente, la entropía se define por la cantidad diferencial  , Donde
, Donde  es la cantidad de calor absorbido en un isotérmica y proceso reversible en la que el sistema va de una estado a otro, y T es la temperatura absoluta a la que se está produciendo el proceso. La entropía es uno de los factores que determina la energía libre del sistema. Esta definición termodinámica de la entropía sólo es válido para un sistema en equilibrio (porque la temperatura se define sólo por un sistema en equilibrio), mientras que la definición estadística de la entropía (ver más abajo) se aplica a cualquier sistema. Así, la definición estadística se considera generalmente como la definición fundamental de la entropía.
es la cantidad de calor absorbido en un isotérmica y proceso reversible en la que el sistema va de una estado a otro, y T es la temperatura absoluta a la que se está produciendo el proceso. La entropía es uno de los factores que determina la energía libre del sistema. Esta definición termodinámica de la entropía sólo es válido para un sistema en equilibrio (porque la temperatura se define sólo por un sistema en equilibrio), mientras que la definición estadística de la entropía (ver más abajo) se aplica a cualquier sistema. Así, la definición estadística se considera generalmente como la definición fundamental de la entropía.
Cambio de entropía a menudo se ha definido como un cambio a una más estado desordenado a un nivel molecular. En los últimos años, la entropía se ha interpretado en términos de la " dispersión "de energía. La entropía es una extenso función de estado que da cuenta de los efectos de irreversibilidad en sistemas termodinámicos.
En cuanto a la mecánica estadística , la entropía describe el número de la posible configuraciones microscópicas del sistema. La definición estadística de la entropía es la definición más fundamental, de la cual todas las demás definiciones y todas las propiedades de la entropía siguen.
Origen del concepto
La primera ley de la termodinámica , formalizado a través de los experimentos al calor de fricción de James Joule en 1843, se ocupa del concepto de energía, la cual es conservada en todos los procesos; la primera ley, sin embargo, carece en su capacidad para cuantificar los efectos de fricción y disipación.
El concepto de entropía se desarrolló en la década de 1850 por el alemán físico Rudolf Clausius quien lo describió como la transformación en el contenido, es decir disipadora de energía uso, de un sistema termodinámico o cuerpo de trabajo de especies químicas durante un cambio de estado.
Aunque el concepto de entropía era originalmente una construcción termodinámico, se ha adaptado en otros campos de estudio, incluyendo teoría de la información, psicodinámica, termoeconomía y evolución .
Historia

La historia de la entropía comienza con el trabajo de Francés matemático Lazare Carnot que en sus 1.803 papel Principios Fundamentales de Equilibrio y Movimiento propusieron que en cualquier máquina de las aceleraciones y choques de las partes en movimiento todos representan pérdidas de momento de actividad. En otras palabras, en cualquier proceso natural existe una tendencia inherente hacia la disipación de la energía útil. Sobre la base de este trabajo, en 1824 el hijo de Lazare Sadi Carnot publicó Reflexiones sobre la potencia motriz del fuego en el que se expone la opinión de que en todos los motores de calor cada vez " calórica ", o lo que ahora se conoce como calor , cae a través de una diferencia de temperatura, que el trabajo o fuerza motriz puede producirse a partir de las acciones de la "caída del calórico" entre un cuerpo caliente y fría. Esta fue una visión anticipada de la segunda ley de la termodinámica .
Carnot basa sus opiniones de calor en parte en la "hipótesis newtoniana" a principios del siglo 18 que el calor y la luz eran tipos de formas indestructibles de materia, que son atraídos y repelidos por otro asunto, y parcialmente en las opiniones contemporáneas de Conde Rumford que mostró en 1789 que el calor podría ser creado por la fricción como cuando se mecanizan orificios de cañón. En consecuencia, Carnot razonó que si el cuerpo de la sustancia de trabajo, tal como un cuerpo de vapor de agua, se lleva de nuevo a su estado original (temperatura y presión) en el extremo de una completa ciclo del motor, que "no se produce cambio en la condición del cuerpo de trabajo." Este último comentario fue modificado en sus notas al pie, y era este comentario que condujo al desarrollo de la entropía.
En la década de 1850 y 60, el físico alemán Rudolf Clausius gravemente opuso a esta última suposición, es decir, que no hay cambio en el cuerpo de trabajo, y se entregó a este "cambio" una interpretación matemática al cuestionar la naturaleza de la pérdida inherente de calor útil cuando se hace el trabajo, por ejemplo, el calor producido por la fricción. Esto fue en contraste con vistas anteriores, en base a las teorías de Isaac Newton , que el calor era una partícula indestructible que tenía masa. Más tarde, los científicos tales como Ludwig Boltzmann, Josiah Willard Gibbs , y James Clerk Maxwell dio la entropía una base estadística. Carathéodory vinculado entropía con una definición matemática de la irreversibilidad, en términos de trayectorias y integrabilidad.
Las definiciones y descripciones
En la ciencia, el término "entropía" se interpreta generalmente de tres formas distintas, sino semi-relacionadas,, es decir, desde el punto de vista macroscópico ( termodinámica clásica ), un punto de vista microscópico ( termodinámica estadística ), y el punto de vista de la información ( teoría de la información).
La definición estadística de la entropía (véase más adelante) es la definición fundamental porque los otros dos pueden ser matemáticamente derivado de él, pero no viceversa. Todas las propiedades de la entropía (incluyendo la segunda ley de la termodinámica ) siguen de esta definición.
Punto de vista macroscópico (termodinámica clásica)
| Variables conjugadas de la termodinámica | |
|---|---|
| Presión | Volumen |
| ( Estrés) | ( Strain) |
| Temperatura | Entropía |
| El potencial químico | Número de la partícula |
En un sistema termodinámico, un "universo" que consiste en "entorno" y "sistemas" y compuesto de cantidades de materia, sus diferencias de presión, las diferencias de densidad, y las diferencias de temperatura todos tienden a igualar en el tiempo - simplemente porque estado de equilibrio tiene mayor probabilidad (más posible combinaciones de microestados) que cualquier otro - ver la mecánica estadística . En el ejemplo de fusión del hielo , la diferencia de temperatura entre una habitación caliente (el entorno) y el vidrio en frío de hielo y agua (el sistema y no parte de la habitación), comienza a ser igualado como porciones de la energía térmica de los alrededores calientes extendido al sistema refrigerador de hielo y agua.

Con el tiempo la temperatura del vidrio y su contenido y la temperatura de la habitación se hacen iguales. La entropía de la habitación ha disminuido como parte de su energía se ha dispersado al hielo y agua. Sin embargo, según lo calculado en el ejemplo, la entropía del sistema de hielo y agua ha aumentado más que la entropía del ambiente circundante ha disminuido. En una sistema aislado como la sala de agua y hielo en su conjunto, la dispersión de energía a partir de más cálido al enfriador siempre resulta en un incremento neto de entropía. Así, cuando el 'universo' del sistema de agua y hielo habitación ha alcanzado un equilibrio de temperatura, el cambio de entropía desde el estado inicial está en un máximo. La entropía del sistema termodinámico es una medida de hasta qué punto la ecualización ha progresado.
Un caso especial de aumento de entropía, la entropía de mezcla, se produce cuando se mezclan dos o más sustancias diferentes. Si las sustancias están a la misma temperatura y presión, no habrá intercambio neto de calor o de trabajo - el aumento de entropía será enteramente debido a la mezcla de las diferentes sustancias.
Desde un punto de vista macroscópico, en la termodinámica clásica la entropía se interpreta simplemente como una función de estado de una sistema termodinámico: es decir, una propiedad que sólo depende del estado actual del sistema, independientemente de cómo se llegó a ese estado a alcanzar. La función de estado tiene la importante propiedad de que, cuando se multiplica por una temperatura de referencia, se puede entender como una medida de la cantidad de energía en un sistema físico que no puede ser utilizado para hacer trabajo termodinámico ; es decir, el trabajo mediado por la energía térmica. Más precisamente, en cualquier proceso en el que el sistema cede energía Δ E, y su entropía disminuye en Δ S, una cantidad al menos T R Δ S de esa energía se debe dar hasta el entorno del sistema como inutilizables calor (T R es el la temperatura de los alrededores externos del sistema). De lo contrario el proceso no seguirá adelante.
En 1862, Clausius declaró lo que él llama el "teorema de equivalencia respetando los valores de las transformaciones" o lo que ahora se conoce como la segunda ley de la termodinámica , como tal:
- La suma algebraica de todas las transformaciones que se producen en un proceso cíclico sólo puede ser positivo, o, en un caso extremo, igual a nada.
Cuantitativamente, Clausius indica la expresión matemática para este teorema es como sigue. Deje δQ ser un elemento del calor emitido por el cuerpo a cualquier reserva de calor durante sus propios cambios, el calor que se puede absorber de un reservorio que se aquí contabilice como negativo, y T la temperatura absoluta del cuerpo en el momento de dar hasta este calor, entonces la ecuación:
debe ser cierto para cada proceso cíclico reversible, y la relación:
debe poseer buena para cada proceso cíclico que es de cualquier manera posible. Esta es la formulación esencial de la segunda ley y una de las formas originales del concepto de entropía. Se puede observar que las dimensiones de la entropía son la energía dividida por la temperatura, que es la misma que las dimensiones de La constante (k B) Boltzmann y capacidad calorífica. La Unidad SI de la entropía es " joule por kelvin "(J · K -1). De esta manera, la cantidad"? S "se utiliza como un tipo de energía interna, que representa los efectos de irreversibilidad, en la ecuación de balance de energía para cualquier sistema dado. En la energía libre de Gibbs ecuación, es decir,? G =? H - TΔS, por ejemplo, que es una fórmula comúnmente utilizado para determinar si las reacciones químicas se producen, la energía relacionada con la entropía cambios TΔS se resta de la? H "total" de energía del sistema para dar el? G energía "libre" del sistema, ya que durante un proceso químico o como cuando un sistema cambia de estado.
Definición microscópica de la entropía (mecánica estadística)
En termodinámica estadística la entropía se define como el número de configuraciones microscópicas que resultan en la observada Descripción macroscópica del sistema termodinámico:
donde
- k B es La constante de Boltzmann 1,38066 × 10 -23 J K-1 y
-
 es el número de microestados correspondientes al macroestado termodinámica observada.
es el número de microestados correspondientes al macroestado termodinámica observada.
Esta definición se considera que es la definición fundamental de la entropía (como todas las otras definiciones pueden ser matemáticamente derivan de ella, pero no viceversa). En 1896 Lectures de Boltzmann sobre Teoría de los gases, mostró que esta expresión da una medida de la entropía para los sistemas de átomos y moléculas en la fase de gas, proporcionando así una medida de la entropía de la termodinámica clásica.
En 1877, Boltzmann visualizó una manera probabilística para medir la entropía de un conjunto de partículas de gas ideal, en la que se definen entropía a ser proporcional al logaritmo del número de microestados un gas tal podría ocupar. A partir de entonces, el problema esencial en la termodinámica estadística , es decir, según Erwin Schrödinger, ha sido determinar la distribución de una determinada cantidad de energía E sobre sistemas idénticos N.
La mecánica estadística explica entropía como la cantidad de incertidumbre (o "mixedupness" en la frase de Gibbs ), que sigue siendo de un sistema, después de que sus propiedades macroscópicas observables se han tenido en cuenta. Para un conjunto dado de variables macroscópicas, como la temperatura y el volumen, la entropía mide el grado en que se extiende la probabilidad de que el sistema a través de diferentes estados cuánticos posibles. Los más estados disponibles para el sistema con mayor probabilidad, mayor es la entropía. Más específicamente, la entropía es una medida logarítmica de la densidad de estados. En esencia, la interpretación más general de la entropía es como una medida de nuestra incertidumbre acerca de un sistema. La estado de equilibrio de un sistema maximiza la entropía porque hemos perdido toda la información acerca de las condiciones iniciales a excepción de las variables conservadas; la maximización de la entropía maximiza nuestra ignorancia acerca de los detalles del sistema. Esta incertidumbre no es del tipo subjetivo cotidiana, sino más bien la incertidumbre inherente al método experimental y modelo interpretativo.
En la escala molecular, las dos definiciones coinciden porque la adición de calor a un sistema, lo que aumenta su entropía termodinámica clásica, también aumenta del sistema fluctuaciones térmicas , dando así un aumento de la falta de información sobre el estado microscópico exacta del sistema, es decir, un aumento entropía mecánica estadística.
El modelo interpretativa tiene un papel central en la determinación de la entropía. El calificativo "para un determinado conjunto de variables macroscópicas" anterior tiene implicaciones muy profundas: si dos observadores utilizan diferentes conjuntos de variables macroscópicas, entonces van a observar diferentes entropías. Por ejemplo, si el observador A utiliza las variables U, V y W, y el observador B utiliza U, V, W, X, entonces, cambiando X, observador B puede causar un efecto que parece una violación de la segunda ley de la termodinámica al observador A. En otras palabras: el conjunto de variables macroscópicas uno elige debe incluir todo lo que puede cambiar en el experimento, de lo contrario se podría ver la disminución de entropía!
La entropía en termodinámica química
La entropía termodinámica es central en termodinámica química, lo que permite que los cambios se cuantifican y el resultado de reacciones predijeron. La segunda ley de la termodinámica afirma que la entropía en la combinación de un sistema y de su entorno (o en una sistema aislado por sí mismo) aumenta durante todos los procesos químicos y físicos espontáneos. La espontaneidad en química significa "por sí mismo, o sin ninguna influencia externa", y no tiene nada que ver con la velocidad. La ecuación de Clausius de δ q rev / T = Δ S introduce la medición del cambio de entropía, Δ S. Cambio de entropía describe la dirección y cuantifica la magnitud de los cambios simples tales como calor transferencia entre sistemas - siempre desde más caliente al enfriador de forma espontánea. Por lo tanto, cuando una mol de sustancia a 0 K es calentado por su entorno a 298 K, la suma de los valores incrementales de q rev / T constituyen cada entropía molar estándar del compuesto del elemento o, una propiedad física fundamental y un indicador de la cantidad de energía almacenada por un sustancia a 298 K. La entropía cambio también mide la mezcla de sustancias como una suma de sus cantidades relativas en la mezcla final.
La entropía es igualmente esencial en la predicción de la magnitud de reacciones químicas complejas, es decir, si un proceso irá como está escrito o proceder en la dirección opuesta. Para tales aplicaciones, Δ S debe ser incorporado en una expresión que incluye tanto el sistema y sus alrededores, Δ S universo = entorno sistema + Δ Δ S S. Esta expresión se convierte, a través de algunos pasos, la energía libre de Gibbs ecuación para reactivos y productos en el sistema: Δ G [la energía libre de Gibbs cambio del sistema] = Δ H [la entalpía cambiar] - T Δ S [el cambio de entropía] .
La segunda ley
Un importante ley de la física, la segunda ley de la termodinámica , establece que la entropía total de cualquier sistema termodinámico aislado tiende a aumentar con el tiempo, acercándose a un valor máximo; y así, implícitamente, la entropía del universo (es decir, el sistema y sus alrededores), asumido como un sistema aislado, tiende a aumentar. Dos consecuencias importantes son que el calor no de sí mismo puede pasar de una más frío a un cuerpo más caliente: es decir, es imposible para transferir calor desde un lugar frío a un depósito caliente sin al mismo tiempo la conversión de una cierta cantidad de trabajo para calentar. También es imposible para cualquier dispositivo que puede funcionar en un ciclo recibir calor de un solo depósito y producir una cantidad neta de trabajo; que sólo se puede conseguir un trabajo útil del calor si el calor es al mismo tiempo transferido desde una caliente a un depósito frío. Esto significa que no hay posibilidad de un hecho aislado " sistema de movimiento perpetuo ". También, de esto se deduce que una reducción en el aumento de entropía en un proceso específico, tal como una reacción química , significa que es energéticamente más eficiente.
En general, de acuerdo con la segunda ley, la entropía de un sistema que no está aislado puede disminuir. Una acondicionador de aire, por ejemplo, enfría el aire en una habitación, lo que reduce la entropía del aire. El calor, sin embargo, que participan en la operación del acondicionador de aire siempre hace una mayor contribución a la entropía del medio ambiente que la disminución de la entropía del aire. Así, la entropía total de la habitación y el medio ambiente aumenta, de acuerdo con la segunda ley.
Ecuación de balance de entropía de los sistemas abiertos
En ingeniería química, los principios de la termodinámica son comúnmente aplicado a " sistemas abiertos ", es decir, aquellos en los que el calor , el trabajo , y la masa de flujo a través de la frontera del sistema. En un sistema en el que hay flujos de tanto calor ( 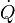 ) Y el trabajo, es decir,
) Y el trabajo, es decir, 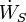 (Trabajo de eje) y P (dV / dt) (trabajo presión-volumen), a través de los límites del sistema, el flujo de calor, pero no el flujo de trabajo, provoca un cambio en la entropía del sistema. Esta tasa de variación de entropía es
(Trabajo de eje) y P (dV / dt) (trabajo presión-volumen), a través de los límites del sistema, el flujo de calor, pero no el flujo de trabajo, provoca un cambio en la entropía del sistema. Esta tasa de variación de entropía es  donde T es el absoluto temperatura termodinámica del sistema en el punto del flujo de calor. Si, además, hay flujos de masas a través de los límites del sistema, la entropía total del sistema también cambiará debido a este flujo por convección.
donde T es el absoluto temperatura termodinámica del sistema en el punto del flujo de calor. Si, además, hay flujos de masas a través de los límites del sistema, la entropía total del sistema también cambiará debido a este flujo por convección.

Para derivar una ecuación equilibrada entropía generalizada, comenzamos con la ecuación del balance general para el cambio en cualquier extensa Θ cantidad en un sistema termodinámico, una cantidad que puede ser o bien conservado, como la energía, o no conservados, como la entropía. La expresión básica equilibrio genérico indica que dΘ / dt, es decir, la tasa de cambio de Θ en el sistema, es igual a la velocidad a la que Θ entra en el sistema en los límites, menos la velocidad a la que Θ deja el sistema a través de los límites del sistema, además de la velocidad a la que Θ se genera dentro del sistema. Usando esta ecuación de balance genérico, con respecto a la tasa de cambio con el tiempo de la extensa cantidad de entropía S, la ecuación de balance de entropía para un sistema termodinámico abierto es:
donde
 = La tasa neta de flujo de la entropía debido a los flujos de masas de entrada y salida del sistema (donde
= La tasa neta de flujo de la entropía debido a los flujos de masas de entrada y salida del sistema (donde  = Entropía por unidad de masa).
= Entropía por unidad de masa).
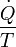 = La tasa de flujo de la entropía debido al flujo de calor a través de la frontera del sistema.
= La tasa de flujo de la entropía debido al flujo de calor a través de la frontera del sistema.
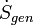 = La tasa de generación interna de entropía dentro del sistema.
= La tasa de generación interna de entropía dentro del sistema.
Tenga en cuenta, también, que si hay múltiples flujos de calor, el término  ha de ser sustituido por
ha de ser sustituido por 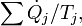 donde
donde 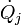 es el flujo de calor y
es el flujo de calor y  es la temperatura en el puerto j-ésimo flujo de calor en el sistema.
es la temperatura en el puerto j-ésimo flujo de calor en el sistema.
La entropía en la mecánica cuántica (von Neumann entropía)
En mecánica estadística cuántica, el concepto de entropía fue desarrollado por John von Neumann y se conoce generalmente como "entropía de von Neumann". Von Neumann estableció el marco matemático correcto para la mecánica cuántica con su trabajo Mathematische Grundlagen der Quantenmechanik. Se proporciona en este trabajo una teoría de la medición, donde la noción habitual de colapso de onda se describe como un proceso irreversible (el llamado von Neumann o medición proyectiva). Usando este concepto, junto con el matriz densidad extendió el concepto clásico de la entropía en el dominio cuántico.
Es bien sabido que una definición basada Shannon de entropía de información conduce en el caso clásico de la entropía de Boltzmann. Es tentador considerar la entropía de Von Neumann como la definición mecánica cuántica correspondiente. Pero este último es problemático desde cuántica punto de información de vista. En consecuencia Stotland, Pomeransky, Bachmat y Cohen han introducido una nueva definición de la entropía que refleja la incertidumbre inherente de los estados de la mecánica cuántica. Esta definición permite distinguir entre la entropía incertidumbre mínimo de estados puros, y el exceso de entropía estadística de mezclas.
Entropía en Astrofísica
En astrofísica, lo que se conoce como "entropía" es en realidad la constante adiabática derivada de la siguiente manera.
El uso de la primera ley de la termodinámica de un proceso infinitesimal cuasi-estática de un sistema hidrostático
Para un gas ideal en este caso especial, la energía interna, U, es sólo una función de T; Por lo tanto, la derivada parcial de la capacidad de calor con respecto a T es idénticamente el mismo que el derivado completa, produciendo a través de alguna manipulación
Además la manipulación utilizando la versión diferencial de la ley de gas ideal, la ecuación anterior, y asumiendo una presión constante, se encuentra
Para un proceso adiabático  y recordando
y recordando 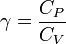 , Se encuentra
, Se encuentra
Se puede resolver esta ecuación diferencial simple de encontrar
Esta ecuación se conoce como una expresión para la constante adiabática, K, también llamado la adiabática. A partir de la ecuación de los gases ideales también se sabe
donde  es la constante de Boltzmann. Sustituyendo esto en la ecuación anterior, junto con
es la constante de Boltzmann. Sustituyendo esto en la ecuación anterior, junto con ![V = [g] / \ rho](../../images/175/17559.png) y
y  para un gas monoatómico ideales se encuentra
para un gas monoatómico ideales se encuentra
donde  es el peso molecular medio del gas o plasma; y
es el peso molecular medio del gas o plasma; y 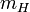 es la masa del átomo de hidrógeno, que es extremadamente cerca de la masa del protón,
es la masa del átomo de hidrógeno, que es extremadamente cerca de la masa del protón,  , Que se utiliza la cantidad más a menudo en la teoría astrofísica de los cúmulos de galaxias. Esto es lo que astrofísicos referirse como "entropía" y tiene unidades de [keV cm 2]. Esta cantidad se refiere a la entropía termodinámica como
, Que se utiliza la cantidad más a menudo en la teoría astrofísica de los cúmulos de galaxias. Esto es lo que astrofísicos referirse como "entropía" y tiene unidades de [keV cm 2]. Esta cantidad se refiere a la entropía termodinámica como
donde  , La densidad de estados en la teoría estadística, toma el valor de K como se definió anteriormente.
, La densidad de estados en la teoría estadística, toma el valor de K como se definió anteriormente.
Definiciones de libros de texto estándar
La siguiente es una lista de definiciones de entropía de una colección de libros de texto. Tenga en cuenta que las definiciones de los libros de texto no son siempre las definiciones más útiles, pero son un aspecto importante de la cultura que rodea al concepto de entropía.
- Entropía - energía desglosado en irrecuperable calor .
- La constante de Boltzmann el logaritmo de una multiplicidad; donde la multiplicidad de una macroestado es el número de microestados que corresponden a la macroestado.
- el número de formas de organizar las cosas en un sistema (los tiempos La constante de Boltzmann).
- un termodinámico no conservada función de estado, medido en términos del número de microestados un sistema pueden asumir, que corresponde a una degradación en utilizable de energía .
- una medida directa de la aleatoriedad de un sistema.
- una medida de dispersión de energía a una temperatura específica.
- una medida de la pérdida parcial de la capacidad de un sistema para realizar el trabajo debido a los efectos de irreversibilidad.
- un índice de la tendencia de un sistema hacia un cambio espontáneo.
- una medida de la falta de disponibilidad de la energía de un sistema para hacer el trabajo; también una medida del desorden; cuanto mayor es la entropía mayor es el trastorno.
- un parámetro que representa el estado de desorden de un sistema en el nivel atómico, iónica o molecular.
- una medida del desorden en el universo o de la disponibilidad de la energía en un sistema para hacer el trabajo.
Los enfoques para la comprensión de la entropía
Orden y desorden
Entropía, históricamente, ha sido a menudo asociada con la cantidad de orden, trastorno, y / o caos en una sistema termodinámico. La definición tradicional de la entropía es que se refiere a los cambios en el status quo del sistema y es una medida de "desorden molecular" y la cantidad de energía desperdiciada en una transformación de la energía dinámica de un estado o forma a otra. En esta dirección, un número de autores, en los últimos años, han derivado fórmulas exactas de entropía para contabilizar y medir desorden y el orden en asambleas atómicas y moleculares. Una de las fórmulas fin entropía / trastorno simple es que derivó en 1984 por el físico termodinámico Peter Landsberg, que se basa en una combinación de la termodinámica y argumentos de la teoría de la información. Landsberg sostiene que cuando las restricciones operan en un sistema, de tal manera que se impide la entrada de uno o más de sus posibles o permitidos estados, en contraste con sus estados prohibidos, la medida de la cantidad total de "desorden" en el sistema viene dada por la siguiente expresión:
Del mismo modo, la cantidad total de "orden" en el sistema viene dada por:
En la que C D es la capacidad de "desorden" del sistema, que es la entropía de las piezas contenidas en el conjunto permitido, C I es la capacidad de "información" del sistema, una expresión similar a Shannon capacidad del canal, y C O es la capacidad de "orden" del sistema.
Dispersión de energía
El concepto de entropía se puede describir cualitativamente como una medida de la dispersión de energía a una temperatura específica. Términos similares han estado en uso desde temprano en la historia de la termodinámica clásica , y con el desarrollo de la termodinámica estadística y la teoría cuántica , cambios de entropía se han descrito en términos de la mezcla o "difusión" de la energía total de cada componente de un sistema sobre sus niveles de energía cuantificados particulares.
Las ambigüedades en el desorden y el caos términos, que normalmente tienen significados opuestos directamente al equilibrio, contribuyen a la confusión generalizada y dificultan la comprensión de la entropía para la mayoría de los estudiantes. A medida que la segunda ley de la termodinámica muestra, en una aislado del sistema porciones internas a diferentes temperaturas tenderán a ajustar a una sola temperatura uniforme y por tanto producen equilibrio. Un enfoque educativo desarrollado recientemente evita términos ambiguos y describe tales propagación de energía en forma de dispersión, lo que conduce a la pérdida de las diferencias requeridas para el trabajo a pesar de que la energía total permanece constante de acuerdo con la primera ley de la termodinámica . Químico físico Peter Atkins, por ejemplo, que previamente escribió de dispersión que conduce a un estado desordenado, ahora escribe que "los cambios espontáneos son siempre acompañados por una dispersión de energía", y ha descartado "desorden" como una descripción.
Entropía y Teoría de la Información
En teoría de la información, la entropía es la medida de la cantidad de información que falta antes de la recepción y se refiere a veces como la entropía de Shannon. La entropía de Shannon es un concepto amplio y general que encuentra aplicaciones en teoría de la información, así como termodinámica. Fue ideado originalmente por Claude Shannon en 1948 para estudiar la cantidad de información en un mensaje transmitido. La definición de la entropía de información es, sin embargo, bastante general, y se expresa en términos de un conjunto discreto de probabilidades  . En el caso de los mensajes transmitidos, estas probabilidades eran las probabilidades de que un mensaje particular fue realmente transmitido, y la entropía del sistema de mensaje era una medida de la cantidad de información era en el mensaje. Para el caso de probabilidades iguales (es decir, cada mensaje es igualmente probable), la entropía de Shannon (en bits) es sólo el número de preguntas sí / no necesarios para determinar el contenido del mensaje.
. En el caso de los mensajes transmitidos, estas probabilidades eran las probabilidades de que un mensaje particular fue realmente transmitido, y la entropía del sistema de mensaje era una medida de la cantidad de información era en el mensaje. Para el caso de probabilidades iguales (es decir, cada mensaje es igualmente probable), la entropía de Shannon (en bits) es sólo el número de preguntas sí / no necesarios para determinar el contenido del mensaje.
La cuestión de la relación entre la entropía de la información y la entropía termodinámica es un tema muy debatido. Algunos autores sostienen que existe una relación entre los dos, mientras que otros argumentan que no tienen absolutamente nada que ver unos con otros.
Las expresiones para las dos entropías son muy similares. La información la entropía H para probabilidades iguales  es:
es:
donde K es una constante que determina las unidades de entropía. Por ejemplo, si las unidades son bits, entonces K = 1 / ln (2). La entropía S termodinámico, desde un punto de vista estadístico mecánica fue expresada por primera vez por Boltzmann:
donde p es la probabilidad de que un sistema de estar en un microestado particular, dado que es en un macroestado en particular, y k es la constante de Boltzmann. Se puede observar que uno puede pensar en la entropía termodinámica como constante, dividido por ln (2), multiplicado por el número de sí de Boltzmann / no hay preguntas que deben ser hechas con el fin de determinar el microestado del sistema, dado que sabemos que la macroestado. El vínculo entre la entropía termodinámica y la información se ha desarrollado en una serie de artículos de Edwin Jaynes a partir de 1957.
El problema con la vinculación de entropía termodinámica de la entropía de información es que en la entropía de información de todo el cuerpo de la termodinámica que se ocupa de la naturaleza física de la entropía no se encuentra. La segunda ley de la termodinámica, que regula el comportamiento de los sistemas termodinámicos en equilibrio, y la primera ley que expresa la energía térmica como el producto de la temperatura y la entropía son conceptos físicos en lugar de conceptos informativos. Si entropía termodinámica es visto como incluyendo todas las dinámicas físicas de entropía, así como los aspectos estadísticos de equilibrio, entonces la entropía de información da sólo una parte de la descripción de entropía termodinámica. Algunos autores, como Tom Schneider, abogan por dejar caer la palabra entropía para la función H de la teoría de la información y utilizando otro término "incertidumbre" de Shannon en su lugar.
Ejemplo de fusión del hielo
La ilustración de este artículo es un ejemplo clásico en el que la entropía aumenta en un pequeño "universo", una sistema termodinámico que consiste en el 'entorno' (la sala caliente) y "sistema" (vidrio, hielo, agua fría). En este universo, algunos calor δQ energía de los alrededores de las habitaciones más cálidas (a 298 K o 25 ° C) se extenderá al sistema refrigerador de hielo y agua en su temperatura constante T de 273 K (0 ° C), la temperatura de fusión de hielo. La entropía del sistema cambiará por la cantidad dS = δQ / T, en este ejemplo δQ / 273 K. (El δQ de calor para este proceso es la energía necesaria para cambiar el agua desde el estado sólido al estado líquido, y se llama la entalpía de fusión, es decir, el ΔH. para la fusión de hielo) La entropía de los alrededores va a cambiar por una cantidaddS= -δQ/ 298 K. Por lo tanto, en este ejemplo, la entropía del sistema aumenta, mientras que la entropía de los alrededores disminuye .
Es importante darse cuenta de que la disminución de la entropía de la habitación circundante es menor que el aumento en la entropía del agua y hielo: la temperatura ambiente de 298 K es mayor que 273 K y por lo tanto la relación, (cambio de entropía), de δQ / 298 K para el entorno es más pequeña que la relación (variación de entropía), de δQ / 273 K para el sistema de agua de hielo +. Para encontrar el cambio de entropía de nuestro "universo", sumamos los cambios de entropía para sus constituyentes: la habitación que rodea, y el hielo + agua. El cambio total de entropía es positivo; esto es siempre cierto en eventos espontáneos en un sistema termodinámico y muestra la importancia predictivo de la entropía: la entropía neto final después de un evento de este tipo es siempre mayor que era la entropía inicial.
Como la temperatura del agua fría se eleva a la de la habitación y la habitación se enfría aún más imperceptible, la suma de la δQ / T en el rango continuo, en muchos incrementos, en el inicialmente fresco para finalmente agua caliente se puede encontrar por cálculo. La miniatura entera "universo", es decir, este sistema termodinámico, se ha incrementado en la entropía. La energía se ha convertido de forma espontánea más disperso y diseminado en el que "universo" que cuando se introdujo el vaso de agua con hielo y se convirtió en un "sistema" en su interior.
Temas en la entropía
Entropía y la vida
Durante más de un siglo y medio, a partir de Clausius 1863 memorias "de la concentración de los rayos de luz y calor, y en los límites de su acción", tanto la escritura y la investigación se ha dedicado a la relación entre la entropía termodinámica y la evolución de la vida . El argumento de que la vida se alimenta de entropía o negativo negatoentropía como poner adelante en el libro 1944 ¿Qué es la vida? por el físico Erwin Schrödinger sirvió como un estímulo más para esta investigación. Escritos recientes han utilizado el concepto de energía libre de Gibbs para la elaboración de este tema. Tangencialmente, algunos creacionistas han argumentado que la entropía descarta evolución .
En los populares libros de texto 1982 Principios de Bioquímica por señalado bioquímico estadounidense Albert Lehninger, por ejemplo, se argumenta que el orden producido dentro de las células a medida que crecen y se dividen es más que compensada por el desorden que crean en su entorno, en el curso del crecimiento y la división. En resumen, de acuerdo con Lehninger, "organismos vivos conservan su orden interno, tomando de su entorno energía libre, en forma de nutrientes o la luz del sol, y volviendo a su entorno una cantidad igual de energía en forma de calor y la entropía. "
Evolución relacionados definiciones:
- Negentropía- una frase coloquial abreviatura de entropía negativa.
- Ectropy- una medida de la tendencia de un sistema dinámico que hacer un trabajo útil y crecer más organizado.
- Syntropy- una tendencia hacia el orden y combinaciones simétricas y diseños de los patrones cada vez más ventajosas y ordenadas.
- Extropy- un término metafórico definir la extensión de la vida o la inteligencia del sistema de organización, orden funcional, la vitalidad, la energía, la vida, la experiencia y la capacidad y la unidad para la mejora y el crecimiento.
- Entropía Ecológica- una medida dela biodiversidaden el estudio de la diversidad biológicaecología.
La flecha del tiempo
La entropía es la única cantidad en las ciencias físicas que los "picos" una dirección particular para el tiempo, a veces llamado una flecha del tiempo. A medida que vamos "hacia adelante" en el tiempo, la segunda ley de la termodinámica nos dice que la entropía de un sistema aislado sólo puede aumentar o permanecer igual; no puede disminuir. Por lo tanto, desde un punto de vista, la medida de la entropía se considera como una especie de reloj.
Entropía y cosmología
Como un universo finito se puede considerar un sistema aislado, puede ser sujeto a la Segunda Ley de la Termodinámica, por lo que su entropía total está en constante aumento. Se ha especulado que el universo está destinado a una muerte térmica en la que toda la energía termina como una distribución homogénea de la energía térmica, por lo que no es obra puede ser extraído de cualquier fuente.
Si el universo se considera que tienen generalmente creciente entropía, entonces - como Roger Penrose ha señalado - la gravedad juega un papel importante en el aumento porque la gravedad hace que la materia dispersa a acumularse en estrellas, que colapso, finalmente, en los agujeros negros . Jacob Bekenstein y Stephen Hawking han demostrado que los agujeros negros tienen la entropía máxima posible de cualquier objeto de igual tamaño. Esto hace que sean puntos finales probable de todos los procesos de entropía creciente, si son trampas de materia y energía totalmente eficaces. Hawking ha, sin embargo, cambió recientemente su postura en este aspecto.
El papel de la entropía en la cosmología sigue siendo un tema controvertido. Trabajos recientes han arrojado extensa en duda la hipótesis de la muerte de calor y la aplicabilidad de cualquier modelo termodinámico simple al universo en general. Aunque la entropía se incrementa en el modelo de un universo en expansión, la entropía máxima posible se eleva mucho más rápidamente - por lo tanto la densidad de entropía está disminuyendo con el tiempo. Esto resulta en una "brecha de entropía" empujando el sistema más lejos de equilibrio. Otros factores que complican, como la densidad de energía del vacío y macroscópicos cuánticos efectos, son difíciles de conciliar con los modelos termodinámicos, hacer predicciones de la termodinámica a gran escala extremadamente difícil.
Otras relaciones
Otras definiciones matemáticas
- Kolmogorov-Sinai entropía- un tipo de matemática de la entropía enlos sistemas dinámicos relacionados con las medidas de particiones.
- Entropía topológica- una forma de definir la entropía en un mapa de función iterada en teoría ergódica.
- Entropía relativa- es una medida natural distancia de una distribución de probabilidad "verdadero"Pa una arbitraria distribución de probabilidadQ.
- Entropía Rényi- una medida de la entropía generalizada para sistemas fractales.
Definiciones sociológicas
El concepto de entropía también ha entrado en el dominio dela sociología, en general, como unametáfora de caos, desorden o la disipación de la energía, en lugar de como una medida directa de la entropía termodinámica o información:
- Entropology- el estudio o discusión de la entropía o el nombre dado a veces ala termodinámicasinecuaciones diferenciales.
- Entropía psicológica- la distribución de energía en la psique, que tiende a buscar el equilibrio o balance entre todas las estructuras de la psique.
- Entropía Económico- una medida semi-cuantitativa de la disipación irrevocable y la degradación de los materiales naturales y la energía disponible con respecto a la actividad económica.
- Entropía social - una medida de la estructura del sistema social, que tiene dos interpretaciones teóricas y estadísticas, es decir, la sociedad (las variables macrosocietal) medido en términos de cómo las funciones individuales en la sociedad (variables microsocietal); También en relación con el equilibrio social.
- Entropía Corporativa - desperdicio de energía como la burocracia y la ineficiencia del equipo de negocio, es decir, la energía perdida a los residuos. (Esta definición es comparable al concepto de de von Clausewitz fricción en la guerra.)
Comillas
| " | Cualquier método que implica la noción deentropía, la existencia misma de la cual depende de lasegunda ley de la termodinámica, será, sin duda, parece que muchos descabellada, y puede repeler a los principiantes como oscuro y difícil de comprender. | " |
- -Willard Gibbs,métodos gráficos en la Termodinámica de Fluidos(1873)
| " | Mi mayor preocupación era cómo llamarlo. Pensé en llamarla "información", pero la palabra estaba acostumbrado demasiado, así que decidí llamarlo "incertidumbre". Cuando hablé con John von Neumann , tuvo una idea mejor. Von Neumann me dijo: 'Usted debe llamarlo entropía , por dos razones. En primer lugar, su función de incertidumbre se ha utilizado en la mecánica estadística bajo ese nombre, por lo que ya cuenta con un nombre. En segundo lugar, y más importante, nadie sabe lo que la entropía es en realidad, por lo que en un debate que siempre tendrá la ventaja. | " |
- --Conversation EntreClaude Shannon yJohn von Neumannen relación con qué nombre dar a la "medida de la incertidumbre" o atenuación en las señales de teléfono de línea (1949)
| " | Cada estrella que arde, cada planeta cuya órbita está decayendo lentamente, cada respiración que usted toma y calorías a metabolizar trae el universo más cerca y más cerca del punto en que se maximiza la entropía, el movimiento organizado de cualquier tipo cesa, y nunca pasa nada nuevo. No hay escapatoria. No importa qué tan magnífica vida en el universo se convierte o cómo avanzado, el lento aumento de la entropía no puede detenerse - el universo finalmente mueren. | " |
- --Warren Friedl, Universidad de Windsor (2007)