
Segunda ley de la termodinámica
Sabías ...
SOS Children ha intentado que el contenido de Wikipedia más accesible por esta selección escuelas. Apadrina un niño para hacer una diferencia real.
| Termodinámica | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 La clásica Máquina de Carnot | |||||||||||||||||||||
Ramas
| |||||||||||||||||||||
Sistemas Estado
Procesos
Ciclos
| |||||||||||||||||||||
|
Propiedades del sistema
Funciones de estado ( Variables conjugadas en cursiva)
| |||||||||||||||||||||
Propiedades materiales
| |||||||||||||||||||||
Ecuaciones
| |||||||||||||||||||||
Potenciales
| |||||||||||||||||||||
Filosofía
Historia
Teorías
Publicaciones clave
Líneas de tiempo
Arte
Educación
| |||||||||||||||||||||
Los científicos
| |||||||||||||||||||||
La segunda ley de la termodinámica dice que la entropía de un sistema aislado nunca disminuye, ya que los sistemas aislados evolucionan espontáneamente hacia equilibrio de la termodinámica estado de máxima entropía. De manera equivalente, máquinas de movimiento perpetuo de la segundo tipo son imposibles.
La segunda ley es un empíricamente validado postulado de la termodinámica , pero puede ser comprendido y explicado mediante las cuántica subyacentes mecánica estadística , junto con el supuesto de baja entropía condiciones iniciales en el pasado distante (posiblemente en el comienzo del universo ). En el lenguaje de la mecánica estadística, la entropía es una medida del número de configuraciones microscópicas que corresponden a un estado macroscópico. Debido equilibrio corresponde a un número mucho mayor de configuraciones microscópicas que cualquier estado de no equilibrio, tiene la máxima entropía y la segunda ley es consecuencia de que el azar solo prácticamente garantiza que el sistema evolucionará hacia el equilibrio.
La segunda ley se piensa que es la fuente de la dirección del tiempo. Es una expresión del hecho de que con el tiempo, las diferencias de temperatura, presión, y disminución potencial químico en un aislado no gravitacional sistema físico, conduciendo finalmente a un estado de equilibrio termodinámico.
La segunda ley puede expresarse de muchas maneras específicas, pero la primera formulación se le atribuye al científico francés Sadi Carnot en 1824 (véase Cronología de la termodinámica).
Descripción
La primera ley de la termodinámica establece la definición básica de energía termodinámica, también llamado energía interna, asociado con todo sistemas termodinámicos, pero desconocido en la mecánica clásica y plantea el estado de conservación de la energía en la naturaleza.
Sin embargo, el concepto de la energía en la primera ley no tiene en cuenta la observación de que los procesos naturales tienen una dirección preferida de progreso. Por ejemplo, el calor siempre fluye espontáneamente de las regiones de mayor temperatura a regiones de temperatura más baja, y nunca a la inversa, a menos que el trabajo externo se lleva a cabo en el sistema. La primera ley es completamente simétrica con respecto a los estados inicial y final de un sistema en evolución. El concepto clave para la explicación de este fenómeno a través de la segunda ley de la termodinámica es la definición de una nueva propiedad física, la entropía .
Un cambio en la entropía (dS) de un sistema es la transferencia infinitesimal de calor (δ Q) a una sistema cerrado la conducción de un proceso reversible, dividido por la temperatura de equilibrio (T) del sistema.
La entropía de un sistema aislado que está en equilibrio es constante y ha alcanzado su valor máximo.
Para un cuerpo en equilibrio térmico con otro, hay un número indefinido de escalas de temperatura empíricos, en general, respectivamente, dependiendo de las propiedades de un cuerpo termométrico particular referencia. El equilibrio térmico entre dos cuerpos implique que tengan igualdad de temperaturas. La ley cero de la termodinámica en su breve declaración habitual permite el reconocimiento de que dos cuerpos tienen la misma temperatura, sobre todo que un organismo de control tiene la misma temperatura que un cuerpo termométrico referencia. La segunda ley permite una escala de temperatura distinguida, que define una, absoluta temperatura termodinámica , independiente de las propiedades de cualquier cuerpo termométrico particular.
La segunda ley de la termodinámica se puede expresar de muchas maneras específicas, las declaraciones clásicos más destacados son la declaración de Rudolph Clausius (1854), la declaración de Lord Kelvin (1851), y la declaración de la termodinámica axiomáticas por Constantin Carathéodory (1909). Estas declaraciones echan la ley en términos físicos generales citando la imposibilidad de ciertos procesos. El Clausius y los estados Kelvin han demostrado ser equivalente.
Una declaración más reciente, debido a George N. Hatsopoulos y Joseph H. Keenan, es: Entre todos los estados de un sistema con dados de energía, los componentes y parámetros, existe un equilibrio estable única que siempre se puede llegar desde cualquier otro estado ( con la misma energía, los componentes y parámetros) por un proceso reversible de peso. El Kelvin-Planck, Clausius y declaraciones Cathedory pueden ser mostrados a seguir a partir de la declaración Hatsopoulos-Keenan.
Enunciado de Clausius
El científico alemán Rudolf Clausius sentó las bases de la segunda ley de la termodinámica en 1850 mediante el examen de la relación entre la transferencia de calor y trabajo. Su formulación de la segunda ley, que fue publicado en alemán en 1854, es conocido como el enunciado de Clausius:
Heat nunca puede pasar de una más frío a un cuerpo más caliente sin algún otro cambio, relacionadas con la misma, que se producen al mismo tiempo.
El calor no puede fluir espontáneamente de las regiones frías a las regiones calientes sin trabajo externo está realizando en el sistema, lo cual es evidente a partir de la experiencia ordinaria de la refrigeración, por ejemplo. En un refrigerador, el calor fluye de frío a caliente, pero sólo cuando se ven obligados por un agente externo, el sistema de refrigeración.
Enunciado de Kelvin
Lord Kelvin expresó la segunda ley como
Es imposible, por medio de agente material inanimado, para derivar efecto mecánico de cualquier porción de materia por enfriamiento por debajo de la temperatura de la más fría de los objetos circundantes.
Principio de Carathéodory
Constantin Carathéodory formulado la termodinámica sobre una base axiomática puramente matemática. Su declaración de la segunda ley se conoce como el Principio de Carathéodory, que puede formularse de la siguiente manera:
En todos los barrios de cualquier S estado de un sistema aislado adiabáticamente hay estados inaccesibles de S.
Con esta formulación se describe el concepto de accesibilidad adiabática por primera vez y sentado las bases de un nuevo subcampo de la termodinámica clásica, a menudo llamados la termodinámica geométricas. Se deduce del principio de Carathéodory que cantidad de energía cuasiestáticamente transferida en forma de calor es un holonómico función de proceso, en otras palabras,  .
.
Aunque es casi habitual en los libros de texto para decir que el principio de Carathéodory expresa la segunda ley y lo tratan como equivalente a la Clausius oa las declaraciones de Kelvin-Planck, tal no es el caso. Para obtener todo el contenido de la segunda ley, el principio de Carathéodory necesita ser complementado por el principio de Planck, que el trabajo isócoro siempre aumenta la energía interna de un sistema cerrado que estaba inicialmente en su propio equilibrio termodinámico interna.
Equivalencia de los estados

Supongamos que hay un motor que viola el enunciado de Kelvin: es decir, una que drena el calor y la convierte completamente en el trabajo de forma cíclica sin ninguna otra consecuencia. Ahora vincularlo con un invertido Motor de Carnot como se muestra en el gráfico. El efecto neto y exclusivo de este motor de nueva creación que consta de los dos motores mencionados es la transferencia de calor  desde el depósito más fresco a la más caliente, lo cual viola el enunciado de Clausius. Así, una violación del enunciado de Kelvin implica una violación del enunciado de Clausius, es decir, el enunciado de Clausius implica el enunciado de Kelvin. Podemos probar de manera similar que el enunciado de Kelvin implica el enunciado de Clausius, y por lo tanto los dos son equivalentes.
desde el depósito más fresco a la más caliente, lo cual viola el enunciado de Clausius. Así, una violación del enunciado de Kelvin implica una violación del enunciado de Clausius, es decir, el enunciado de Clausius implica el enunciado de Kelvin. Podemos probar de manera similar que el enunciado de Kelvin implica el enunciado de Clausius, y por lo tanto los dos son equivalentes.
En los sistemas gravitacionales
En los sistemas no gravitatorios objetos siempre tienen positivo capacidad de calor, lo que significa que la temperatura aumenta con la energía. Por lo tanto, cuando los flujos de energía a partir de un objeto de alta temperatura a una baja temperatura, la temperatura de la ex se disminuye mientras que la temperatura de este último se incrementa; por lo tanto, las diferencias de temperatura tienden a disminuir con el tiempo.
Sin embargo, este no es siempre el caso para sistemas en los que la fuerza gravitacional es importante. Los ejemplos más notables son los agujeros negros, que - según la teoría - tener capacidad calorífica negativo. El más grande es el agujero negro, más energía que contiene, pero el menor es su temperatura. Por lo tanto, la agujero negro supermasivo en el centro de la Vía Láctea se supone que tiene una temperatura de 10 -14 K, mucho más bajo que el fondo cósmico de microondas temperatura de 2.7K, pero a medida que absorbe los fotones del fondo cósmico de microondas de su masa está aumentando de manera que su baja temperatura disminuye aún más con el tiempo.
Por esta razón, los sistemas gravitacionales tienden hacia la no-distribución uniforme de masa y energía. Si bien esto es opuesta a la forma en que la segunda ley opera en otras circunstancias, en realidad es un consquence de la segunda ley.
Corolarios
El movimiento perpetuo de segunda especie
Antes del establecimiento de la Segunda Ley, muchas personas que estaban interesadas en la invención de una máquina de movimiento perpetuo habían tratado de eludir las restricciones de la Primera Ley de la Termodinámica , extrayendo la energía interna masiva del medio ambiente como la potencia de la máquina. Dicha máquina se llama una "máquina de movimiento perpetuo de segunda especie". La segunda ley declara la imposibilidad de este tipo de máquinas.
Carnot teorema
Teorema de Carnot (1824) es un principio que limita la eficiencia máxima para cualquier posible del motor. La eficiencia depende únicamente de la diferencia de temperatura entre los depósitos térmicos calientes y frías. Teorema de Carnot:
- Todos los motores térmicos irreversibles entre dos depósitos de calor son menos eficientes que un Máquina de Carnot que opera entre los mismos depósitos.
- Todos los motores de calor reversibles entre dos depósitos de calor son igualmente eficientes con una máquina de Carnot que opera entre los mismos depósitos.
En su modelo ideal, el calor de calorías convertida en trabajo podría ser reintegrado invirtiendo el movimiento del ciclo, un concepto, posteriormente conocido como reversibilidad termodinámico. Sin embargo más Carnot postula que algunos calórico se pierde, no se conviertan en trabajo mecánico. Por tanto, ninguna máquina térmica real podría darse cuenta de la Reversibilidad de Carnot ciclo y fue condenado a ser menos eficiente.
Aunque formulado en términos de calorías (véase el obsoleto teoría calórica), en lugar de la entropía , se trataba de una visión anticipada de la segunda ley.
Clausius Desigualdad
La Clausius Teorema (1854) afirma que en un proceso cíclico
La igualdad se cumple en el caso reversible y la '<' es en el caso irreversible. El caso reversible se utiliza para introducir la función de estado de entropía . Esto es porque en procesos cíclicos de la variación de una función de estado es cero a partir de la funcionalidad de estado.
Temperatura termodinámica
Para un motor térmico arbitraria, la eficiencia es:
donde A es el trabajo realizado por ciclo. Así, la eficiencia depende sólo de q C / q H.
El teorema de Carnot establece que todos los motores reversibles que operan entre los mismos depósitos de calor son igualmente eficientes. Por lo tanto, cualquier motor de calor reversible que opera entre las temperaturas T 1 y T 2 debe tener la misma eficiencia, es decir, la eficiencia es la función de sólo temperaturas: 
Además, un motor de calor reversible que opera entre las temperaturas T 1 y T 3 debe tener la misma eficiencia como uno que consta de dos ciclos, uno entre T 1 y otro (intermedio) la temperatura T 2, y el segundo entre T 2 y T 3. Esto sólo puede ser el caso si
Consideremos ahora el caso en el que  es una temperatura de referencia fijo: la temperatura de la punto triple del agua. Entonces para cualquier T 2 y T 3,
es una temperatura de referencia fijo: la temperatura de la punto triple del agua. Entonces para cualquier T 2 y T 3,
Por lo tanto si la temperatura termodinámica se define por
entonces la función f, visto como una función de la temperatura termodinámica, es simplemente
y la temperatura de referencia T 1 tendrá el valor 273.16. (Por supuesto, cualquier temperatura de referencia y cualquier valor numérico positivo podrían utilizar-la elección aquí corresponde a la Kelvin escala.)
Entropía
De acuerdo con la Igualdad de Clausius, para un proceso reversible
Eso significa que la integral de línea  es camino independiente.
es camino independiente.
Así podemos definir una función de estado llama entropía, que satisface
Con este sólo podemos obtener la diferencia de la entropía mediante la integración de la fórmula anterior. Para obtener el valor absoluto, necesitamos la tercera ley de la termodinámica , que establece que S = 0 en el cero absoluto de cristales perfectos.
Para cualquier proceso irreversible, ya que la entropía es una función de estado, podemos conectarnos siempre el estado inicial y terminal con un proceso reversible imaginario y la integración en ese camino para calcular la diferencia de entropía.
Ahora revertir el proceso reversible y combinarlo con el citado proceso irreversible. Aplicando Clausius desigualdad en este bucle,
Por lo tanto,
donde la igualdad se cumple si la transformación es reversible.
Observe que si el proceso es una proceso adiabático, a continuación,  , Por lo
, Por lo  .
.
Disponible trabajo útil
Un caso especial idealizada importante y revelador es considerar la aplicación de la segunda ley de la situación de un sistema aislado (llamado sistema total o universo), compuesto de dos partes: un sub-sistema de interés, y los alrededores del sub-sistema. Estos alrededores son imaginadas a ser tan grande que se pueden considerar como un depósito de calor ilimitado a la temperatura T y la presión P R R - de modo que la cantidad no importa el calor se transfiere a (o desde) el sub-sistema, la temperatura de la entorno permanecerán T R; y no importa lo mucho que el volumen del sub-sistema se expande (o contratos), la presión de los alrededores permanecerá P R.
Sean cuales sean los cambios a DS y DS R ocurren en las entropías de la sub-sistema y el entorno de forma individual, de acuerdo con la segunda ley de la entropía S tot del total del sistema aislado no debe disminuir:
De acuerdo con la primera ley de la termodinámica , el cambio dU en la energía interna del sub-sistema es la suma del calor δq añade al subsistema, menos cualquier δw trabajo realizado por el sub-sistema, más cualquier energía química neta entrar en el sub-sistema de d Σμ iR N i, de modo que:
donde μ iR son la potenciales químicos de las especies químicas en los alrededores externos.
Ahora el calor que sale del depósito y entra en el sub-sistema es
donde hemos utilizado primero la definición de entropía en termodinámica clásica (alternativamente, en la termodinámica estadística, la relación entre el cambio de entropía, la temperatura y el calor absorbido se puede derivar); y luego la segunda desigualdad Ley desde arriba.
De ello se deduce que cualquier δw trabajo neto realizado por el subsistema debe obedecer
Es útil para separar el δw trabajo realizado por el subsistema en el trabajo útil δw u que se puede hacer por el sub-sistema, más allá de la R dV trabajo p hecho simplemente por el sub-sistema en expansión contra la presión externa que rodea, dando la siguiente relación para el trabajo útil que se puede hacer:
Es conveniente definir la mano del lado derecho como el derivado exacta de un potencial termodinámico, llamada la disponibilidad o exergía X del subsistema,
Por consiguiente, la segunda ley implica que para cualquier proceso que puede ser considerado como dividido simplemente en un subsistema, y una temperatura ilimitado y depósito de presión con la que está en contacto,
es decir, el cambio en la exergía del subsistema más el trabajo útil realizado por el subsistema (o, el cambio en la exergía del subsistema menos cualquier trabajo, adicional a la realizada por el depósito de presión, realizado en el sistema) debe ser menor o igual a cero .
En suma, si se elige un estado de referencia infinita-depósito-como adecuado como el entorno del sistema en el mundo real, entonces la Segunda Ley predice una disminución de X para un proceso irreversible y ningún cambio para un proceso reversible.
 Es equivalente a
Es equivalente a 
Esta expresión, junto con el estado de referencia asociado permite una ingeniero de diseño que trabaja en la escala macroscópica (por encima de la límite termodinámico) para utilizar la segunda ley sin medir directamente o considerando el cambio de entropía en un sistema aislado total. (Vea también ingeniero de procesos). Esos cambios ya han sido considerados por la suposición de que el sistema que se considere puede alcanzar el equilibrio con el estado de referencia sin alterar el estado de referencia. Una eficacia de un proceso o conjunto de procesos que lo compara con el ideal reversible también puede ser encontrado (Ver segundo eficiencia ley.)
Este enfoque de la segunda ley es ampliamente utilizado en la ingeniería práctica, contabilidad ambiental, ecología de sistemas, y otras disciplinas.
Historia
La primera teoría de la conversión de calor en trabajo mecánico se debe a Nicolas Léonard Sadi Carnot en 1824. Él fue el primero en darse cuenta correctamente que la eficacia de esta conversión depende de la diferencia de temperatura entre un motor y su entorno.
Reconociendo la importancia de El trabajo de James Prescott Joule sobre la conservación de la energía, Rudolf Clausius fue el primero en formular la segunda ley durante 1850, en esta forma: el calor no fluye espontáneamente de frío a cuerpos calientes. Mientras que el conocimiento común ahora, esto era contrario a la teoría del calórico popular en ese entonces, que considera el calor como un fluido. A partir de ahí fue capaz de inferir el principio de Sadi Carnot y la definición de la entropía (1865).
Fundada en el siglo 19, la Enunciado de Kelvin-Planck de la segunda ley dice: "Es imposible para cualquier dispositivo que opera en un ciclo para recibir calor de un solo reservorio y producir una cantidad neta de trabajo. "Esto ha demostrado ser equivalente a la afirmación de Clausius.
La hipótesis ergódico también es importante para la Enfoque de Boltzmann. Se dice que, durante largos períodos de tiempo, el tiempo de permanencia en alguna región del espacio de fase de microestados con la misma energía es proporcional al volumen de esta región, es decir, que todos los microestados accesibles son igualmente probables durante un largo período de tiempo. De manera equivalente, se dice que el tiempo promedio y promedio en el conjunto estadístico son los mismos.
Se ha demostrado que no sólo los sistemas clásicos, sino también de la mecánica cuántica los tienden a maximizar su entropía en el tiempo. Así, la segunda ley sigue, dada las condiciones iniciales con baja entropía. Más precisamente, se ha demostrado que lo local von Neumann entropía está en su valor máximo con una probabilidad muy alta. El resultado es válido para una gran clase de sistemas cuánticos aislados (por ejemplo, un gas en un recipiente). Si bien el sistema completo es puro y por lo tanto no tiene ninguna entropía, la entrelazamiento entre el gas y el recipiente da lugar a un aumento de la entropía local del gas. Este resultado es uno de los logros más importantes de termodinámica cuántica.
Hoy en día, mucho esfuerzo en el campo está tratando de entender por qué las condiciones iniciales tempranas en el universo fueron las de baja entropía, ya que esto se considera como el origen de la segunda ley (ver más abajo).
Descripciones informales
La segunda ley puede establecer de varias formas breves, incluyendo:
- Es imposible para producir trabajo en el entorno usando un proceso cíclico conectado a un solo depósito de calor ( Kelvin , 1851).
- Es imposible llevar a cabo un proceso cíclico utilizando un motor conectado a dos depósitos de calor que tendrá como su único efecto de la transferencia de una cantidad de calor desde el depósito a baja temperatura para el depósito de alta temperatura ( Clausius, 1854).
- Si termodinámico trabajo que se debe hacer a una velocidad finita, energía libre debe ser gastado. (Stoner, 2000)
Descripciones matemáticas
En 1856, el físico alemán Rudolf Clausius declaró lo que él llama el "segundo teorema fundamental en la teoría mecánica del calor "en la siguiente forma:
donde Q es el calor, T es la temperatura y N es la "equivalencia-valor" de todas las transformaciones no compensados que intervienen en un proceso cíclico. Más tarde, en 1865, Clausius vendría a definir la "equivalencia-valor", como la entropía. En los talones de esta definición, ese mismo año, la versión más famosa de la segunda ley fue leída en una presentación en la Sociedad Filosófica de Zurich el 24 de abril, en el que, al final de su presentación, Clausius concluye:
La entropía del universo tiende a un máximo.
Esta declaración es el fraseo más conocido de la segunda ley. Además, debido a la amplitud general de la terminología utilizada aquí, por ejemplo, universo , así como la falta de condiciones específicas, por ejemplo, abierto, cerrado o aislado, al que se aplica esta declaración, mucha gente toma esta simple declaración en el sentido de que la segunda ley de la termodinámica se aplica prácticamente a todos los temas imaginables. Esto, por supuesto, no es cierto; esta declaración es sólo una versión simplificada de una descripción más compleja.
En cuanto a la variación en el tiempo, el enunciado matemático de la segunda ley de un sistema aislado de someterse a una transformación arbitraria es:
donde
- S es la entropía del sistema y
- t es el tiempo .
El signo de igualdad es válido en el caso de que sólo los procesos reversibles tienen lugar en el interior del sistema. Si los procesos irreversibles tienen lugar (que es el caso en los sistemas reales en funcionamiento) la> -sign bodegas. Una forma alternativa de formulación de la segunda ley para sistemas aislados es:
 con
con 
con  la suma de la tasa de producción de entropía por todos los procesos en el interior del sistema. La ventaja de esta formulación es que muestra el efecto de la producción de entropía. La tasa de producción de entropía es un concepto muy importante, ya que determina (límites) la eficiencia de las máquinas térmicas. Multiplicado con temperatura ambiente
la suma de la tasa de producción de entropía por todos los procesos en el interior del sistema. La ventaja de esta formulación es que muestra el efecto de la producción de entropía. La tasa de producción de entropía es un concepto muy importante, ya que determina (límites) la eficiencia de las máquinas térmicas. Multiplicado con temperatura ambiente  da la llamada energía disipada
da la llamada energía disipada  .
.
La expresión de la segunda ley para sistemas cerrados (por lo que, lo que permite el intercambio de calor y los límites en movimiento, pero no cambio de la materia) es:
 con
con 
Aquí
 es el flujo de calor en el sistema de
es el flujo de calor en el sistema de  es la temperatura en el punto donde el calor entra en el sistema.
es la temperatura en el punto donde el calor entra en el sistema.
Si el calor se suministra con el sistema en varios lugares que tenemos que tomar la suma algebraica de los términos correspondientes.
Para los sistemas abiertos (también permite el intercambio de materia):
 con
con 
Aquí  es el flujo de la entropía en el sistema asociado con el flujo de entrar en la materia el sistema. No se debe confundir con la derivada temporal de la entropía. Si la materia se suministra en varios lugares que tenemos que tomar la suma algebraica de estas contribuciones.
es el flujo de la entropía en el sistema asociado con el flujo de entrar en la materia el sistema. No se debe confundir con la derivada temporal de la entropía. Si la materia se suministra en varios lugares que tenemos que tomar la suma algebraica de estas contribuciones.
La mecánica estadística da una explicación para la segunda ley postulando que una materia se compone de átomos y moléculas que están en constante movimiento. Un conjunto particular de posiciones y velocidades de cada partícula en el sistema se denomina una microestado del sistema y debido al constante movimiento, el sistema está cambiando constantemente su microestado. La mecánica estadística postula que, en equilibrio, cada microestado que el sistema podría estar en la misma probabilidad de ocurrir, y cuando se hace esta suposición, que conduce directamente a la conclusión de que la segunda ley debe mantener en un sentido estadístico. Es decir, la segunda ley celebrará en promedio, con una variación estadística en el orden de 1 / √ N, donde N es el número de partículas en el sistema. Para situaciones cotidianas (macroscópicos), la probabilidad de que la segunda ley se violó es prácticamente cero. Sin embargo, para sistemas con un número pequeño de partículas, los parámetros termodinámicos, incluyendo la entropía, pueden mostrar desviaciones estadísticas significativas de la predicha por la segunda ley. Teoría termodinámica clásica no se ocupa de estas variaciones estadísticas.
Derivación de la mecánica estadística
Debido a La paradoja de Loschmidt, derivaciones de la Segunda Ley tiene que hacer una suposición con respecto al pasado, a saber, que el sistema es no correlacionado en algún momento en el pasado; esto permite para el tratamiento probabilístico simple. Este supuesto se lo suele considerar como un condición de frontera, por lo que la segunda ley es en última instancia una consecuencia de las condiciones iniciales en algún lugar en el pasado, probablemente a comienzos del universo (el Big Bang ), aunque otros escenarios también se han sugerido.
Teniendo en cuenta estas premisas, en la mecánica estadística, la segunda ley no es un postulado, sino que es una consecuencia del postulado fundamental , también conocido como el postulado igual probabilidad a priori, siempre y cuando uno es claro que los argumentos simples de probabilidad sólo se aplican a la futuro, mientras que para el pasado hay fuentes auxiliares de información que nos dicen que era de baja entropía. La primera parte de la segunda ley, que establece que la entropía de un sistema aislado térmicamente sólo puede aumentar es una consecuencia trivial de la igualdad postulado probabilidad a priori, si se restringe la noción de la entropía de los sistemas en equilibrio térmico. La entropía de un sistema aislado en equilibrio térmico que contiene una cantidad de energía de 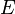 es:
es:
donde  es el número de estados cuánticos en un pequeño intervalo entre
es el número de estados cuánticos en un pequeño intervalo entre 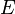 y
y  . Aquí
. Aquí  es un macroscópicamente pequeño intervalo de energía que se considera como base. Estrictamente hablando, esto significa que la entropía depende de la elección de
es un macroscópicamente pequeño intervalo de energía que se considera como base. Estrictamente hablando, esto significa que la entropía depende de la elección de  . Sin embargo, en el límite termodinámico (es decir, en el límite de tamaño infinitamente grande del sistema), la entropía específica (entropía por unidad de volumen o por unidad de masa) no depende de
. Sin embargo, en el límite termodinámico (es decir, en el límite de tamaño infinitamente grande del sistema), la entropía específica (entropía por unidad de volumen o por unidad de masa) no depende de  .
.
Supongamos que tenemos un sistema aislado cuyo estado macroscópico es especificado por un número de variables. Estas variables macroscópicas pueden, por ejemplo, se refieren al volumen total, las posiciones de los pistones en el sistema, etc. Entonces  dependerá de los valores de estas variables. Si una variable no es fijo, (por ejemplo, no abrazadera de un pistón en una cierta posición), a continuación, porque todos los estados accesibles son igualmente probables en equilibrio, la variable libre en equilibrio será tal que
dependerá de los valores de estas variables. Si una variable no es fijo, (por ejemplo, no abrazadera de un pistón en una cierta posición), a continuación, porque todos los estados accesibles son igualmente probables en equilibrio, la variable libre en equilibrio será tal que  se maximiza ya que es la situación más probable en equilibrio.
se maximiza ya que es la situación más probable en equilibrio.
Si la variable se fijó inicialmente a algún valor a continuación, después de la liberación y cuando se ha alcanzado el nuevo equilibrio, el hecho de la variable se ajustará de manera que  se maximiza, implica que la entropía habrá aumentado o se han mantenido igual (si el valor en que se haya fijado la variable pasó a ser el valor de equilibrio).
se maximiza, implica que la entropía habrá aumentado o se han mantenido igual (si el valor en que se haya fijado la variable pasó a ser el valor de equilibrio).
La entropía de un sistema que no está en equilibrio se puede definir como:
ver aquí . Aquí el  se las probabilidades de que el sistema se pueden encontrar en los estados marcados por el subíndice j. En equilibrio térmico las probabilidades de los estados dentro del intervalo de energía
se las probabilidades de que el sistema se pueden encontrar en los estados marcados por el subíndice j. En equilibrio térmico las probabilidades de los estados dentro del intervalo de energía  son todos iguales a
son todos iguales a  , Y en ese caso la definición general coincide con la definición anterior de S que se aplica al caso de equilibrio térmico.
, Y en ese caso la definición general coincide con la definición anterior de S que se aplica al caso de equilibrio térmico.
Supongamos que partimos de una situación de equilibrio y de repente eliminamos una restricción en una variable. Luego a la derecha después de hacer esto, hay una serie  de microestados accesibles, pero aún no se ha alcanzado el equilibrio, por lo que las probabilidades reales del sistema que se está en un cierto estado accesible aún no son igual a la probabilidad previa de
de microestados accesibles, pero aún no se ha alcanzado el equilibrio, por lo que las probabilidades reales del sistema que se está en un cierto estado accesible aún no son igual a la probabilidad previa de  . Ya hemos visto que en el estado final de equilibrio, la entropía habrá aumentado o ha permanecido igual en relación con el estado de equilibrio anterior. Boltzmann H-teorema, sin embargo, demuestra que la entropía aumentará continuamente como una función del tiempo durante el cabo intermedio de estado de equilibrio.
. Ya hemos visto que en el estado final de equilibrio, la entropía habrá aumentado o ha permanecido igual en relación con el estado de equilibrio anterior. Boltzmann H-teorema, sin embargo, demuestra que la entropía aumentará continuamente como una función del tiempo durante el cabo intermedio de estado de equilibrio.
Derivación de la variación de entropía para procesos reversibles
La segunda parte de la segunda ley establece que el cambio de entropía de un sistema de someterse a un proceso reversible viene dada por:
donde la temperatura se define como:
Ver aquí para la justificación de esta definición. Supongamos que el sistema tiene algún parámetro externo, x, que puede ser cambiado. En general, los estados propios de energía del sistema dependerá de x. De acuerdo con la teorema adiabático de la mecánica cuántica, en el límite de un cambio infinitamente lenta del hamiltoniano del sistema, el sistema permanecerá en el mismo estado propio de energía y por lo tanto cambiar su energía de acuerdo con el cambio en la energía de la energía de estado propio que se encuentra.
La fuerza generalizada, X, correspondiente a la variable externa x se define de tal manera que  es el trabajo realizado por el sistema si x se incrementa en una cantidad dx. Por ejemplo, si x es el volumen, entonces X es la presión. La fuerza generalizada de un sistema conocido para estar en estado propio de energía
es el trabajo realizado por el sistema si x se incrementa en una cantidad dx. Por ejemplo, si x es el volumen, entonces X es la presión. La fuerza generalizada de un sistema conocido para estar en estado propio de energía  es dado por:
es dado por:
Dado que el sistema puede estar en cualquier estado propio de energía dentro de un intervalo de  , Definimos la fuerza generalizada para el sistema como el valor esperado de la expresión anterior:
, Definimos la fuerza generalizada para el sistema como el valor esperado de la expresión anterior:
Para evaluar la media, dividimos el  estados propios de energía contando cuántos de ellos tienen una relación calidad-
estados propios de energía contando cuántos de ellos tienen una relación calidad-  dentro de un rango entre
dentro de un rango entre  y
y  . Al llamar a este número
. Al llamar a este número  , Tenemos:
, Tenemos:
El promedio de la definición de la fuerza generalizada ahora se puede escribir:
Podemos relacionar esto con la derivada de la entropía wrt x en energía constante E como sigue. Supongamos que cambiamos x a x + dx. Entonces  va a cambiar porque los estados propios de energía dependen de x, causando estados propios energía para mover dentro o fuera del rango de entre
va a cambiar porque los estados propios de energía dependen de x, causando estados propios energía para mover dentro o fuera del rango de entre 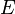 y
y  . Vamos a centrarnos de nuevo en los estados propios de energía para los que
. Vamos a centrarnos de nuevo en los estados propios de energía para los que  se encuentra dentro del rango entre
se encuentra dentro del rango entre  y
y  . Dado que estos estados propios de energía aumentan en energía por Y dx, todos esos estados propios de energía que se encuentran en el intervalo que va desde E - Y dx a E movimiento desde abajo E para arriba E. Hay
. Dado que estos estados propios de energía aumentan en energía por Y dx, todos esos estados propios de energía que se encuentran en el intervalo que va desde E - Y dx a E movimiento desde abajo E para arriba E. Hay
dichos estados propios de energía. Si  , Todos estos estados propios de energía se moverán en un rango entre
, Todos estos estados propios de energía se moverán en un rango entre 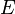 y
y  y contribuir a un aumento de la
y contribuir a un aumento de la  . El número de estados propios de energía que se mueven desde abajo
. El número de estados propios de energía que se mueven desde abajo  anteriormente
anteriormente  está, por supuesto, dada por
está, por supuesto, dada por  . La diferencia
. La diferencia
es, pues, la contribución neta al aumento de  . Tenga en cuenta que si Y es más grande que dx
. Tenga en cuenta que si Y es más grande que dx  habrá los estados propios de energía que se mueven desde abajo E para arriba
habrá los estados propios de energía que se mueven desde abajo E para arriba  . Se cuentan en tanto
. Se cuentan en tanto  y
y  , Por lo tanto, la expresión anterior es válido también en ese caso.
, Por lo tanto, la expresión anterior es válido también en ese caso.
Expresando la expresión anterior como un derivado wrt E y sumando sobre Y se obtiene la expresión:
La derivada logarítmica de wrt x está dada entonces por:
wrt x está dada entonces por:
El primer término es intensivo, es decir, que no se escala con el tamaño del sistema. En contraste, el último término escalas como el tamaño del sistema inverso y así lo hará desaparece en el límite termodinámico. Así, hemos encontrado que:
Combinando esto con
Da:
Derivación de sistemas descritos por el conjunto canónico
Si un sistema está en contacto térmico con un baño de calor en algún temperatura T a continuación, en equilibrio, la distribución de probabilidad sobre los valores propios de la energía vienen dados por elconjunto canónico:
Aquí Z es un factor que normaliza la suma de todas las probabilidades a 1, esta función se conoce como la función de partición. Consideremos ahora un cambio reversible infinitesimal en la temperatura y en los parámetros externos en los que los niveles de energía dependen. Se desprende de la fórmula general para la entropía:
que
Inserción de la fórmula para el conjunto canónico aquí da:
el conjunto canónico aquí da:
Derivación general de unitaridad de la mecánica cuántica
El operador tiempo de desarrollo de la teoría cuántica es unitario, porque el hamiltoniano es hermitiano. En consecuencia, la matriz de probabilidad de transición es doblemente estocástica, lo que implica la Segunda Ley de la Termodinámica. Esta derivación es bastante general, basado en la entropía de Shannon, y no requiere ninguna hipótesis más allá de unitaridad, que es universalmente aceptada. Es una consecuencia de la irreversibilidad o la naturaleza singular de la matriz de transición general.
Estados de no equilibrio
Es sólo por convención, para los fines de análisis termodinámico, que cualquier ocasión arbitraria del espacio-tiempo se dice que está en equilibrio termodinámico. En general, una ocasión del espacio-tiempo que se encuentra en la naturaleza no está en equilibrio termodinámico, interpretado en los términos más estrictos. En términos más flexibles, nada en todo el universo es o ha sido alguna vez verdaderamente en equilibrio termodinámico exacta. Si se supone, para los fines de análisis físicos, que uno está tratando con un sistema en equilibrio termodinámico, a continuación, estadísticamente es posible para ese sistema para lograr momentos de no equilibrio. En tales eventos estadísticamente improbables donde las partículas calientes "roban" la energía de las partículas frías suficientes de que el lado frío se enfría y el lado caliente se pone más caliente, por un instante. Tales eventos se han observado en una pequeña escala lo suficientemente donde la probabilidad de que tal cosa suceda es significativo.
La física involucrada en este tipo de eventos es el tema del teorema de fluctuación (que no debe confundirse con el teorema de fluctuación-disipación), probado por Denis Evans y Debra Searles, da una estimación numérica de la probabilidad de que un sistema fuera de equilibrio tendrá un cierto cambio en la entropía más de una cierta cantidad de tiempo. El teorema se demuestra con la hora exacta ecuaciones dinámicas reversibles de movimiento, pero asume el axioma de causalidad, que es equivalente a suponer condiciones iniciales no correlacionados (es decir, no correlacionadas últimos). Predicciones cuantitativas de este teorema se han confirmado en experimentos de laboratorio en la Universidad Nacional de Australia realizadas por Edith M. Sevick et al. uso aparato de pinzas ópticas.
Flecha del tiempo
La segunda ley de la termodinámica es la única ley física, aparte deciertas interacciones raras en la física de partículas, que no es simétrica a la inversión del sentido del tiempo.
La segunda ley se piensa que es la razón de la diferencia entre el movimiento hacia adelante y hacia atrás en el tiempo, tales como por qué la causa precede al efecto (la flecha causal de tiempo).
Controversias
Demonio de Maxwell
James Clerk Maxwell imaginó un contenedor dividido en dos partes, A y B . Ambas partes se llenan con el mismo gas a temperaturas iguales y se colocan uno junto al otro. Observando las moléculas en ambos lados, un imaginario demonio guarda una trampilla entre las dos partes. Cuando una molécula más rápido que el promedio de A vuela hacia la trampilla, el demonio lo abre, y la molécula volará desde A a B . La media la velocidad de las moléculas en B habrá aumentado mientras que en A se han ralentizado en promedio. Puesto que la velocidad molecular medio corresponde a la temperatura, la temperatura disminuye en A y el aumento de B , en contra de la segunda ley de la termodinámica.
Una de las respuestas más famosos a esta pregunta fue sugerido en 1929 por Leo Szilard y más tarde por Léon Brillouin. Szilárd señaló que en la vida real demonio de Maxwell tendría que tener algún medio de la medición de la velocidad molecular, y que el acto de adquisición de información requeriría un gasto de energía. Pero se encontraron excepciones posteriores.
La paradoja de Loschmidt
La paradoja de Loschmidt, también conocida como la paradoja de reversibilidad, es la objeción de que no debería ser posible deducir un proceso irreversible de la dinámica en tiempo simétrica. Esto pone el tiempo de simetría reversión de los procesos físicos fundamentales casi todos los conocidos de nivel bajo en desacuerdo con cualquier intento de inferir de ellos la segunda ley de la termodinámica, que describe el comportamiento de los sistemas macroscópicos. Ambos son principios bien aceptada en física, con el apoyo observacional y teórica sólida, sin embargo, parecen estar en conflicto; por lo tanto, la paradoja.
Debido a esta paradoja, derivaciones de la segunda ley tienen que hacer una suposición con respecto al pasado, a saber, que el sistema es no correlacionado en algún momento en el pasado, o - lo que es equivalente - que la entropía en el pasado fue menor que en el futuro. Este supuesto se lo suele considerar como una condición de frontera, por lo que la segunda ley se deriva en última instancia de las condiciones iniciales del Big Bang .
Gibbs paradoja
En la mecánica estadística , un simple derivación de la entropía de un gas ideal basado en la distribución de Boltzmann produce una expresión para la entropía que no es extensa (no es proporcional a la cantidad de gas en cuestión). Esto lleva a una aparente paradoja conocida como la paradoja de Gibbs, permitiendo, por ejemplo, la entropía de un sistema cerrado para disminuir, violar la segunda ley de la termodinámica.
La paradoja se evita mediante el reconocimiento de que la identidad de las partículas no influye en la entropía. En la explicación convencional, esto se asocia con un indistinguishability de las partículas asociadas con la mecánica cuántica. Sin embargo, un número creciente de documentos ahora tomar la perspectiva de que no es más que la definición de la entropía que se cambia de ignorar la permutación de las partículas (y de ese modo evitar la paradoja). La ecuación resultante para la entropía (de un gas ideal clásico) es extensa, y es conocida como la ecuación Sackur-Tetrode.
Poincaré recurrencia teorema
La Poincaré recurrencia teorema establece que determinados sistemas, después de un tiempo suficientemente largo, volver a un estado muy cercano al estado inicial. El tiempo de recurrencia de Poincaré es el período de tiempo transcurrido hasta la recurrencia, que es del orden de  . El resultado se aplica a los sistemas físicos en los que se conserva la energía. El teorema de recurrencia aparentemente contradice la segunda ley de la termodinámica, que dice que los grandes sistemas dinámicos evolucionan irreversiblemente hacia el estado con mayor entropía, por lo que si se parte de un estado de baja entropía, el sistema nunca volver a ella. Hay muchas maneras posibles de resolver esta paradoja, pero ninguna de ellas es universalmente aceptado. El argumento más razonable es que para los sistemas termodinámicos típicos del tiempo de recurrencia es tan grande (muchas veces más largo que el tiempo de vida del universo) que, a efectos prácticos, no se puede observar la recurrencia.
. El resultado se aplica a los sistemas físicos en los que se conserva la energía. El teorema de recurrencia aparentemente contradice la segunda ley de la termodinámica, que dice que los grandes sistemas dinámicos evolucionan irreversiblemente hacia el estado con mayor entropía, por lo que si se parte de un estado de baja entropía, el sistema nunca volver a ella. Hay muchas maneras posibles de resolver esta paradoja, pero ninguna de ellas es universalmente aceptado. El argumento más razonable es que para los sistemas termodinámicos típicos del tiempo de recurrencia es tan grande (muchas veces más largo que el tiempo de vida del universo) que, a efectos prácticos, no se puede observar la recurrencia.
Muerte térmica del universo
De acuerdo con la segunda ley, la entropía de cualquier sistema aislado, como el universo entero, nunca disminuye. Si la entropía del universo no tiene máximo límite superior entonces eventualmente el universo no tendrá energía libre termodinámica para sostener el movimiento o la vida , es decir, el que se alcanza la muerte de calor.
Citas
| Wikiquote tiene una colección de citas relacionadas con: Segunda ley de la termodinámica |
La ley que la entropía siempre aumenta sostiene, en mi opinión, la posición suprema entre las leyes de la Naturaleza. Si alguien señala a usted que su teoría favorita del universo está en desacuerdo con las ecuaciones de Maxwell - entonces tanto peor para las ecuaciones de Maxwell. Si se comprueba que se contradice con la observación - bueno, estos experimentadores hacen cosas bungle veces. Pero si su teoría se encuentra para estar en contra de la segunda ley de la termodinámica que puedo darle ninguna esperanza; no hay nada para ella, pero a colapsar en la humillación más profunda.-SirArthur Stanley Eddington,La naturaleza del mundo físico(1927)
La tendencia a la entropía de aumentar en sistemas aislados se expresa en la segunda ley de la termodinámica - quizás la formulación más pesimista y amoral en todo el pensamiento humano.- Gregory Hill yKerry Thornley, Principia Discordia(1965)
Ha habido casi tantas formulaciones de la segunda ley como ha habido discusiones de la misma.-Philosopher / FísicoPW Bridgman, (1941)



































![S = k \ log \ left [\ Omega \ dejó (E \ right) \ right] \,](../../images/2567/256780.png)


![\ Frac {1} {k T} \ equiv \ beta \ equiv \ frac {d \ log \ left [\ Omega \ dejó (E \ right) \ right]} {de}](../../images/2567/256788.png)
















