Masa

En la física , la masa (de griego μᾶζα "pan de cebada, a tanto alzado (de masa)") se refiere a la cantidad de materia en un objeto. Más específicamente, la masa inercial es una medida cuantitativa de la resistencia de un objeto a la aceleración . Además de esto, la masa gravitacional es una medida cuantitativa que es proporcional a la magnitud de la fuerza gravitacional que es

1. ejercida por un objeto (masa gravitacional activo), o
2. experimentado por un objeto (fuerza gravitacional pasivo)

al interactuar con un segundo objeto. La Unidad SI de masa es el kilogramo (kg).

En el uso diario, la masa se refiere a veces como " peso ", las unidades de las cuales pueden ser libras o kilogramos (por ejemplo, el peso de una persona puede ser declarado como 75 kg). En uso científico, sin embargo, el término" peso "se refiere a una diferentes, pero relacionadas propiedad de la materia,. El peso es la fuerza gravitacional que actúa sobre un cuerpo, lo cual dada varía en función de la fuerza de gravedad del cuerpo opuesto (por ejemplo, el peso de una persona en la Tierra vs sobre la Luna ) - mientras que la masa es una propiedad intrínseca de ese cuerpo que nunca cambia. En otras palabras, el peso de un objeto depende de su medio ambiente, mientras que su masa no. En la superficie de la Tierra, un objeto con una masa de 50 kilogramos pesa 491 newtons; en la superficie de la Luna, el mismo objeto todavía tiene una masa de 50 kilogramos, pero pesa sólo 81,5 newtons. Reexpresado en términos matemáticos, en la superficie de la Tierra, el peso W de un objeto está relacionada con su masa m por W = m g, donde g = 9,806 6 5 m / s ² es la El campo gravitacional de la Tierra, (expresado como la aceleración experimentada por un objeto en caída libre).

La masa inercial de un objeto determina su aceleración en la presencia de una fuerza aplicada. De acuerdo con la segunda ley de Newton del movimiento , si un cuerpo de masa m fijo se somete a una fuerza F sola, su aceleración a es dada por ^F / _m. La masa de un cuerpo también determina el grado en que se genera o se ve afectada por una campo gravitatorio. Si un primer cuerpo de masa m _A se coloca a una distancia r (centro de masa de centro de masa) de un segundo cuerpo de masa m _B, cada cuerpo experimenta una fuerza de atracción F _g = Gm _A m _B / r ^2, donde G = 6,67 × 10 ^-11 kg N ^-2 m ² es el "universal .. la constante gravitacional "Esto se refiere a veces como masa gravitatoria experimentos repetidos desde el siglo 17 han demostrado que la masa inercial y gravitatoria son equivalentes; desde 1915, esta observación se ha conllevado a priori en el principio de equivalencia de la relatividad general .

La relatividad especial muestra que masa en reposo (o masa invariante) y energía en reposo son esencialmente equivalentes, a través de la relación bien conocida E = mc ^2. Esta misma ecuación también se conecta masa relativista y "energía relativista" (energía total del sistema). Los dos últimos masa "relativista" y la energía son conceptos que están relacionados con sus contrapartes "descanso", pero no tienen el mismo valor que sus contrapartes de descanso en los sistemas donde hay un momento neto. Con el fin de deducir cualquiera de estas cuatro cantidades de cualquiera de los otros, en cualquier sistema que tiene un momento neto, se necesita una ecuación que toma en cuenta el impulso. Masa (siempre que el tipo y la definición de masa está acordado) es una cantidad conservada en el tiempo. Desde el punto de vista de un solo observador no acelerado, la masa no se crea ni se destruye, y la relatividad especial no cambia esta comprensión. Todos los observadores no acelerado de acuerdo en la cantidad de masa invariante en sistemas cerrados en todo momento, y aunque diferentes observadores no pueden ponerse de acuerdo entre sí sobre cuánto masa relativista está presente en cualquier sistema, todos coinciden en que la cantidad no cambia con el tiempo.

Macroscópicamente, la masa se asocia con la materia asunto -aunque, a diferencia de masa, está mal definido en la ciencia. En la escala subatómica, no sólo fermiones, las partículas a menudo asociados con la materia, sino también algunos bosones, las partículas que actúan como portadores de fuerza, tener masa en reposo. Otro problema para una fácil definición es que gran parte de la masa en reposo de la materia ordinaria se deriva de la masa invariante contribuyó a la materia de partículas y energías cinéticas que han dejado de masa en reposo a sí mismos (sólo el 1% de la masa en reposo de la materia se explica por el resto masa de sus quarks fermionic y electrones). Desde una perspectiva fundamental de la física, la masa es el número que describe en las que el representación de la pequeño grupo de la Grupo de Poincaré transforma una partícula. En el Modelo Estándar de la física de partículas, esta simetría se describe como algo que surge como consecuencia de un acoplamiento de partículas con masa en reposo a un postulado adicional campo, conocido como el Campo de Higgs.

La masa total del universo observable se estima entre 10 y ⁵² kg 10 kg ^53, correspondiente a la masa en reposo de entre 10 ⁷⁹ y 10 ⁸⁰ protones .

Las unidades de masa

El kilogramo es una de las siete unidades de base del SI ; Entre éstos, es uno de los tres, incluyendo el segundo y el kelvin , que se definen ad hoc, sin referencia a otra unidad base. Desde 1889, el kilogramo se definió por medio del kilogramo prototipo internacional .

Balanzas permiten comparar directamente masa gravitacional dentro de un campo gravitatorio. Estos dispositivos han estado en uso por lo menos desde la Edad del Bronce Medio (que se muestra es un equilibrio para pesar citas tabaco de la mitad del siglo 19).

En el Sistema Internacional de Unidades (SI), la masa se mide en kilogramos (kg). El gramo (g) es _^1/1000 de un kilogramo. El programa fue introducido por primera vez en 1795, con una definición basada en la densidad del agua (de modo que en la temperatura de fusión del hielo , un centímetro cúbico de agua tendría una masa de un gramo, mientras que el metro en el momento se definió como el 10000000mo parte de la distancia desde el ecuador de la Tierra a la Polo Norte). Desde 1889, el kilogramo se ha definido como la masa del kilogramo prototipo internacional , y como tal es independiente de la metro, o las propiedades del agua. En octubre de 2011, el día 24 Conferencia General de Pesas y Medidas resolvieron "tomar nota de la intención de" redefinir el kilogramo en términos de la Constante de Planck, previsto para 2014.

Otras unidades son aceptados para su uso en el SI:

• La tonelada (t) es igual a 1,000 kg.
• La electronvolt (eV) es principalmente una unidad de energía , pero a causa de la la equivalencia masa-energía también puede funcionar como una unidad de masa. En este contexto, se denota eV / c ^2, o simplemente como eV. El electronvolt es común en la física de partículas .
• La unidad de masa atómica (u) se define de manera que un solo átomo de carbono-12 tiene una masa de 12 u; 1 U es aproximadamente 1,66 × 10 ^-27 kg. La unidad de masa atómica es conveniente para expresar las masas de los átomos y las moléculas.

Fuera del sistema SI, se utiliza una variedad de diferentes unidades de masa, dependiendo del contexto, como el babosa (sl), la libras (lb), la Masa de Planck (m _P), y el masa solar.

En situaciones normales, el peso de un objeto es proporcional a su masa, que por lo general hace que sea problemático utilizar la misma unidad en ambos conceptos. Sin embargo, el distinción entre masa y peso llega a ser importante para las mediciones con una precisión mejor que un pequeño porcentaje (debido a ligeras diferencias en la fuerza de la Del campo gravitatorio en diferentes lugares de la Tierra), y para los lugares alejados de la superficie de la Tierra, como en el espacio o en otros planetas.

Una masa a veces se puede expresar en términos de longitud. La masa de una partícula muy pequeña puede ser identificado con su inversa Compton longitud de onda (1 cm ^-1 ≈ 3.52 × 10 ^-41 kg). La masa de una estrella muy grande o agujero negro puede ser identificado con su Radio de Schwarzschild (1 cm ≈ 6.73 × 10 ²⁴ kg).

Resumen de los conceptos de masa y formalismos

En la mecánica clásica , la masa tiene un papel central en la determinación del comportamiento de los cuerpos. La segunda ley de Newton relaciona la fuerza F ejercida en un cuerpo de masa m a del cuerpo de aceleración a:

.

Además, la masa se refiere de un cuerpo impulso p a su lineal velocidad v:

,

y del cuerpo de energía cinética K a su velocidad:

.

En la relatividad especial , masa relativista es un formalismo que representa los efectos relativistas haciendo que el aumento de la masa con la velocidad.

Dado que la energía es dependiente de marco de referencia (al observador), es conveniente formular las ecuaciones de la física de tal manera que los valores de masa son invariantes (no cambie) entre los observadores, y así las ecuaciones son independientes del observador. Para una sola partícula, esta cantidad es la masa en reposo; para un sistema de partículas dependiente o independiente, esta cantidad es la masa invariante. La masa invariante M de un cuerpo está relacionada con su energía E y la magnitud de su impulso p por

donde c es la velocidad de la luz .

Resumen de los conceptos relacionados con la masa

La relación entre las propiedades de masa y sus constantes físicas asociadas. Se cree Cada objeto masivo para exhibir las cinco propiedades. Sin embargo, debido a las constantes extremadamente grandes o extremadamente pequeños, es generalmente imposible verificar más de dos o tres propiedades para cualquier objeto.

• La Radio de Schwarzschild (r _s) representa la capacidad de la masa para provocar curvatura en el espacio y el tiempo.
• La parámetro gravitacional estándar (μ) representa la capacidad de un cuerpo masivo para ejercer fuerzas gravitacionales newtonianos en otros cuerpos.
• La masa inercial (m) representa la respuesta newtoniana de masa de fuerzas.
• Energía en reposo (E ₀₎ representa la capacidad de la masa para ser convertido en otras formas de energía.
• La Compton longitud de onda (λ) representa la respuesta cuántica de la masa a la geometría local.

En la ciencia física , se pueden distinguir conceptualmente entre al menos siete aspectos diferentes de la masa, o siete nociones físicas que involucran el concepto de masa:

• La cantidad de materia en ciertos tipos de muestras se puede determinar con exactitud a través de electrodeposición u otros procesos precisas . La masa de una muestra exacta está determinada en parte por el número y tipo de átomos o moléculas que contiene, y en parte por la energía implicada en la unión juntos (que contribuye un negativo "masa perdida", o déficit de masa).

• La masa inercial es una medida de la resistencia de un objeto a cambiar su estado de movimiento cuando una fuerza se aplica. Se determina mediante la aplicación de una fuerza a un objeto y la medición de la aceleración que resulta de esa fuerza. Un objeto con pequeña masa inercial se acelerará más de un objeto con gran masa inercial cuando actúa sobre la misma fuerza. Se dice que el cuerpo de mayor masa tiene mayor inercia.

• Masa gravitacional activa (* ver más adelante) es una medida de la fuerza de un objeto de flujo gravitacional (flujo gravitacional es igual a la integral de superficie de campo gravitatorio sobre una superficie envolvente). Campo gravitacional se puede medir permitiendo que un pequeño 'objeto de prueba' caer libremente y midiendo su aceleración en caída libre. Por ejemplo, un objeto en caída libre cerca de la luna experimentará menos campo gravitatorio, y por lo tanto acelerar más lento que el mismo objeto haría si estuviera en caída libre cerca de la Tierra. El campo gravitacional cerca de la Luna es más débil porque la Luna tiene masa gravitatoria menos activo.

• Masa gravitacional pasiva (* ver más adelante) es una medida de la fuerza de la interacción de un objeto con una campo gravitatorio. Masa gravitatoria pasivo se determina dividiendo el peso de un objeto por su aceleración en caída libre. Dos objetos dentro del mismo campo gravitatorio experimentarán la misma aceleración; sin embargo, el objeto con una masa gravitacional más pequeño pasiva experimentará una fuerza más pequeña (menos peso) que el objeto con una masa gravitacional pasiva más grande.

• La energía también tiene masa de acuerdo con el principio de la equivalencia masa-energía. Esta equivalencia se ejemplifica en un gran número de procesos físicos incluyendo la producción de pares, la fusión nuclear, y la gravitatoria flexión de la luz. La producción de pares y la fusión nuclear son procesos mediante los cuales cantidades mensurables de masa y energía se convierten en unos de otros. En la curvatura gravitatoria de la luz, los fotones de energía pura se muestran a exhibir un comportamiento similar a masa gravitacional pasiva.

• La curvatura de el espacio-tiempo es una manifestación relativista de la existencia de la masa. Curvatura es extremadamente débil y difícil de medir. Por esta razón, la curvatura no fue descubierto hasta después de que fue predicho por la teoría de la relatividad general de Einstein. Extremadamente precisa los relojes atómicos en la superficie de la tierra, por ejemplo, se encuentran a medir menos tiempo (correr más lento) que los relojes similares en el espacio. Esta diferencia en el tiempo transcurrido es una forma de curvatura llamada la dilatación del tiempo gravitacional. Otras formas de curvatura se han medido utilizando el Satélite Gravity Probe B.

• Masa Quantum se manifiesta como una diferencia entre cuántica de un objeto frecuencia y su número de onda. La masa cuántica del electrón, la Compton longitud de onda, se puede determinar a través de diversas formas de espectroscopía y está estrechamente relacionado con el Rydberg constante, la Radio de Bohr, y la radio clásico del electrón. La masa cuántica de objetos de mayor tamaño se puede medir directamente usando una balanza watt. En la mecánica cuántica relativista, la masa es una de las etiquetas representación irreducible del grupo de Poincaré.

* NOTA: La distinción entre "activo" y "pasivo" masa gravitatoria no existe en la visión newtoniana de la gravedad como se encuentra en la mecánica clásica , y con seguridad puede ser ignorado por los laicos. (En la mayoría de las aplicaciones prácticas, la gravedad newtoniana se utiliza debido a que por lo general es suficientemente precisa, y es más simple que la relatividad general, por ejemplo, la NASA usa la gravedad newtoniana principalmente para diseñar misiones espaciales, aunque "precisiones se han mejorado de forma rutinaria por la contabilidad para pequeños efectos relativistas" .) La distinción entre "activo" y "pasivo" es muy abstracto, y se aplica a las aplicaciones de nivel de post-grado de la Relatividad General a ciertos problemas en la cosmología, y de otra manera no se utiliza. Hay, sin embargo, una importante distinción conceptual de la física newtoniana entre "masa inercial" y "masa gravitacional", aunque estas cantidades son idénticos; la distinción conceptual entre estas dos definiciones fundamentales de la masa se mantiene con fines de enseñanza, porque implican dos métodos distintos de medición. Durante mucho tiempo se considera anómalo que las dos medidas distintas de la masa (inercial y gravitacional) dieron el mismo resultado. La propiedad observada, señalado por Galileo, según la cual los objetos de diferente caída masiva con el mismo ritmo de aceleración (ignorando la resistencia del aire), es una expresión del hecho de que la masa inercial y gravitacional son iguales.

En resumen, cada experimento hasta la fecha ha demostrado los siete valores anteriores para ser proporcional, y en algunos casos iguales, y esta proporcionalidad da lugar al concepto abstracto de la masa. Si, en algún experimento futuro, uno de los fenómenos de masas relacionada se muestra no ser proporcional a los demás, entonces ese fenómeno específico ya no se considera una parte del concepto abstracto de la masa.

El peso y la cantidad

Representación de principios balanzas en la Papiro de Hunefer (datada en el 19a dinastía, ca. 1285 aC). Los espectáculos de escena Anubis pesando el corazón de Hunefer.

Peso, por definición, es una medida de la fuerza que debe aplicarse para apoyar un objeto (es decir, mantenga en reposo) en un campo gravitatorio. Campo gravitatorio de la Tierra hace que elementos cercanos a la Tierra que tienen peso. Por lo general, los campos gravitacionales cambian sólo ligeramente en distancias cortas, y el campo de la Tierra es casi uniforme en todos los lugares en la superficie de la Tierra; Por lo tanto, el peso de un objeto cambia ligeramente cuando se mueve de un lugar a otro, y estos pequeños cambios pasó desapercibido durante gran parte de la historia. Esto puede haber dado los primeros seres humanos la impresión de que el peso es una propiedad que no cambia, fundamental de los objetos en el mundo material. Además, la medición de peso utilizando una balanza no se ve afectada por los cambios en la intensidad del campo gravitatorio, y por lo que este no era un problema en los primeros tiempos.

En el egipcio ilustración religiosa a la derecha, Anubis está utilizando una balanza para pesar el corazón de Hunefer. La balanza equilibra la fuerza del peso de un objeto contra la fuerza del peso de otro objeto. Los dos lados de una balanza son lo suficientemente cerca que los objetos experimentan campos gravitacionales similares. Por lo tanto, si tienen masas similares a continuación, sus pesos también será similar. Esto permite que la escala, por los pesos que comparan, para comparar también las masas, y le da la distinción de ser uno de los dispositivos más antiguos conocidos capaces de medir la masa.

El concepto de cantidad es muy antiguo y es anterior a la historia, por lo que cualquier descripción de los primeros desarrollos de este concepto es de naturaleza especulativa. Sin embargo, se podría suponer razonablemente que los seres humanos, en algún era temprana, se dieron cuenta de que el peso de una colección de objetos similares era directamente proporcional al número de objetos de la colección:

donde W es el peso de la colección de objetos similares y n es el número de objetos de la colección. Proporcionalidad, por definición, implica que dos valores tienen una constante relación:

, O equivalentemente

En consecuencia, los estándares de peso históricos a menudo se definen en términos de cantidades. Los romanos, por ejemplo, utiliza la semilla de algarrobo ( quilates o siliqua) como un estándar de medición. Si el peso de un objeto es equivalente a 1728 semillas de algarrobo, a continuación, el objeto se dijo que pesar una libra romana. Si, por otra parte, el peso del objeto era equivalente a 144 semillas de algarrobo entonces el objeto se dice que pesan una onza romana (Uncia). La libra romana y oz ambos fueron definidos en términos de diferentes colecciones de tamaño de un mismo patrón de masa común, la semilla de algarrobo. La relación de una onza romano (144 semillas de algarrobo) a una libra romana (1728 semillas de algarrobo) fue:

Este ejemplo ilustra una ocurrencia común en la ciencia física: cuando los valores se relacionan a través de fracciones simples, hay una buena posibilidad de que los valores se derivan de una fuente común.

Varios átomos y moléculas como se muestran en John Dalton Un nuevo sistema 's de filosofía química (1808)

El nombre átomo proviene del griego ἄτομος / Átomos, α-τέμνω, lo que significa uncuttable, algo que no se puede dividir aún más. El concepto filosófico que la materia podría estar compuesto por unidades discretas que no pueden ser divididas a su vez ha sido de alrededor de milenios. Sin embargo, la prueba empírica y la aceptación universal de la existencia de los átomos no se produjo hasta el siglo 20.

A medida que la ciencia de la química maduró, evidencia experimental de la existencia de los átomos vino de la la ley de las proporciones múltiples. Cuando dos o más elementos combinados para formar un compuesto, sus masas están siempre en una relación fija y definida. Por ejemplo, la relación de masa de nitrógeno a oxígeno en el óxido nítrico es siete ochos. El amoniaco tiene un hidrógeno a nitrógeno relación de masa de tres catorceavos. El hecho de que las masas elementales combinan en fracciones simples sugiere que toda la masa elemental se deriva de una fuente común. En principio, la situación masa atómica es análogo al ejemplo anterior de unidades de masa romanos. La libra romana y oz ambos fueron definidos en términos de diferentes colecciones clasificadas por tamaño de semillas de algarrobo, y, en consecuencia, las dos unidades de masa se relacionan entre sí a través de una fracción simple. Comparativamente, ya que todas las masas atómicas se relacionan entre sí a través de fracciones simples, entonces tal vez las masas atómicas son sólo diferentes colecciones de tamaño de alguna unidad de masa fundamental común.

En 1805, el químico John Dalton publicó su primera tabla de pesos atómicos relativos, enumerando seis elementos, hidrógeno , oxígeno , nitrógeno , carbono , azufre y fósforo , y la asignación de hidrógeno un peso atómico de 1. Y en 1815, el químico William Prout llegó a la conclusión de que el átomo de hidrógeno era de hecho la unidad de masa fundamental de la cual se derivan todas las otras masas atómicas.

Los átomos de carbono en grafito (Imagen obtenida con Scanning tunneling microscopio)

Si La hipótesis de Prout había demostrado exacta, entonces el concepto abstracto de la masa, como la conocemos ahora, nunca podría haber evolucionado, ya que la masa siempre podría definirse en términos de cantidades de la masa atómica de hidrógeno. La hipótesis de Prout; sin embargo, se encontró que ser inexacta en dos aspectos principales. En primer lugar, nuevos avances científicos revelaron la existencia de partículas más pequeñas, tales como electrones y quarks , cuyas masas no están relacionados a través de fracciones simples. Y en segundo lugar, las masas elementales sí se encontró que no sea múltiplo exacto de la masa átomo de hidrógeno, sino más bien, eran cerca de múltiplos. La teoría de la relatividad de Einstein explicó que cuando los protones y neutrones se unen para formar un núcleo atómico , algo de la masa del núcleo se libera en forma de energía de unión. Cuanto más fuertemente unido el núcleo, más energía se pierde durante la formación y esta pérdida de energía de enlace hace que las masas elementales no ser relacionados a través de fracciones simples.

El hidrógeno, por ejemplo, con un solo protón, tiene un peso atómico de 1.007825 u. El más abundante isótopos de hierro tiene 26 protones y 30 neutrones, por lo que uno podría esperar su peso atómico sea 56 veces mayor que la del átomo de hidrógeno, pero de hecho, su peso atómico es sólo 55,9383 u, lo que claramente no es un número entero múltiplo de 1,007825. La hipótesis de Prout fue probada inexacta en muchos aspectos, pero los conceptos abstractos de la masa atómica y la cantidad siga desempeñando un papel influyente en la química y la unidad de masa atómica sigue siendo la unidad de elección para mediciones de masa muy pequeñas.

Misas para su uso con balanzas

Cuando los franceses inventaron el sistema métrico en el siglo 18, utilizaron una cantidad de definir su unidad de masa. El kilogramo fue originalmente definido para que sea igual en masa a la cantidad de agua pura contenida en un recipiente de un litro. Esta definición, sin embargo, fue insuficiente para los requisitos de precisión de la tecnología moderna, y el kilogramo métrico se redefinió en términos de una barra de platino-iridio hecho por el hombre conocido como el kilogramo prototipo internacional.

Masa gravitacional

Masa gravitacional activa es una propiedad de la masa de un objeto que produce un campo gravitacional en el espacio que rodea al objeto, y estos campos gravitatorios gobernar estructuras a gran escala en el Universo . Campos gravitacionales tienen las galaxias juntas. Causan nubes de gas y polvo a unirse en estrellas y planetas . Ellos proporcionan la presión necesaria para la fusión nuclear que se produzca dentro de las estrellas. Y determinan la órbitas de varios objetos dentro del Sistema Solar . Puesto que los efectos gravitacionales están a nuestro alrededor, es imposible precisar la fecha exacta en que los seres humanos descubrieron masa gravitatoria. Sin embargo, es posible identificar algunos de los pasos importantes hacia nuestra comprensión moderna de la masa gravitatoria y su relación con los otros fenómenos de masas. Algunos términos asociados con masa gravitacional y sus efectos son los Constante gravitacional gaussiana, la parámetro gravitacional estándar y el Radio de Schwarzschild.

Masa gravitatoria kepleriano

Johannes Kepler 1610

Inglés nombre		Los planetas de Kepler
		Semieje mayor	Período orbital sideral	Misa de Sun
Mercurio		0.387 099 AU	0.240 842 año sideral
Venus		0,723 332 UA	0,615 187 años sideral
Tierra		1.000 000 UA	1.000 000 años sideral
Marte		1.523 662 UA	1.880 816 años sideral
Júpiter		5.203 363 UA	11,861 776 años sideral
Saturno		9.537 070 UA	29,456 626 años sideral

Johannes Kepler fue el primero en dar una descripción precisa de las órbitas de los planetas, y de esta manera; él fue el primero en describir la masa gravitatoria. En 1600 AD, Kepler buscó empleo con Tycho Brahe y en consecuencia tuvo acceso a los datos astronómicos de una precisión más alta que cualquier previamente disponible. Utilizando observaciones precisas de Brahe del planeta Marte, Kepler se dio cuenta de que los métodos astronómicos tradicionales eran inexactos en sus predicciones, y pasó los próximos cinco años a desarrollar su propio método para caracterizar el movimiento planetario.

En el modelo planetaria final de Kepler, que describió con éxito las órbitas planetarias como siguiente elípticas caminos con el Sol en un punto focal de la elipse. El concepto de masa gravitatoria activo es una consecuencia inmediata de Kepler tercera ley del movimiento planetario . Kepler descubrió que la cuadrado de la período orbital de cada planeta es directamente proporcional a la cubo de la semieje mayor de su órbita, o equivalente, que la relación de estos dos valores es constante para todos los planetas del Sistema Solar . Esta relación constante es una medida directa de la masa gravitacional activa del Sol, cuenta con unidades de distancia en cubos por tiempo al cuadrado, y es conocido como el parámetro gravitacional estándar:

Inglés nombre		Las lunas galileanas
		Semieje mayor	Período orbital sideral	Masa de Júpiter
Io		0.002 819 UA	0.004 843 años sideral
Europa		0.004 486 UA	0,009 722 años sideral
Ganímedes		0.007 155 UA	0,019 589 años sideral
Callisto		0.012 585 UA	0.045 694 años sideral

En 1609, Johannes Kepler publicó sus tres reglas conocidas como leyes de Kepler del movimiento planetario, explicando cómo los planetas siguen órbitas elípticas bajo la influencia del Sol El 25 de agosto de ese mismo año, Galileo Galilei demostró su primer telescopio a un grupo de mercaderes venecianos, ya principios de enero de 1610, Galileo observó cuatro objetos tenues cerca de Júpiter, que confundió con estrellas. Sin embargo, después de unos días de observación, Galileo se dio cuenta de que estas "estrellas" eran, de hecho, que orbita a Júpiter. Estos cuatro objetos (más tarde llamado el Lunas galileanas en honor de su descubridor) fueron los primeros cuerpos celestes observados en orbitar algo que no sea la Tierra o Sol Galileo continuó observando estas lunas en los próximos dieciocho meses, y para mediados de 1611 había obtenido estimaciones muy precisas de sus períodos. Más tarde, el semi-eje mayor de cada luna también se estimó, permitiendo así que la masa gravitacional de Júpiter que se determina a partir de las órbitas de sus lunas. La masa gravitacional de Júpiter se encontró que era aproximadamente una milésima de la masa gravitacional del Sol

Campo gravitatorio galileo

Galileo Galilei 1636

Distancia recorrida por una bola en caída libre es proporcional al cuadrado del tiempo transcurrido

En algún momento antes de 1638, Galileo dirigió su atención al fenómeno de la caída de objetos bajo la influencia de la gravedad de la Tierra, y que estaba tratando activamente de caracterizar estos movimientos. Galileo no fue el primero en investigar el campo gravitatorio de la Tierra, ni fue el primero en describir con precisión sus características fundamentales. Sin embargo, la dependencia de Galileo en la experimentación científica para establecer principios físicos tendría un profundo efecto en las futuras generaciones de científicos. Galileo utilizó una serie de experimentos científicos para caracterizar el movimiento de caída libre. No está claro si se trataba de experimentos sólo hipotéticas utilizadas para ilustrar un concepto, o si eran experimentos reales realizados por Galileo, pero los resultados obtenidos en estos experimentos fueron a la vez realista y convincente. Una biografía por alumno de Galileo Vincenzo Viviani afirmó que Galileo había caído bolas del mismo material, pero diferentes masas, desde la torre inclinada de Pisa para demostrar que su tiempo de descenso era independiente de su masa. En apoyo de esta conclusión, Galileo había avanzado el siguiente argumento teórico: Me preguntó si dos cuerpos de masas diferentes y distintos ritmos de caída están atadas por una cuerda, ¿el sistema combinado caen más rápido, ya que ahora es más masiva, o hace el encendedor cuerpo en su caída más lenta contuvo el cuerpo más pesado? La única solución convincente a esta pregunta es que todos los cuerpos deben caer en la misma proporción.

Un experimento posterior se describe en dos nuevas ciencias de Galileo publicados en 1638. Uno de los personajes de ficción de Galileo, Salviati, describe un experimento utilizando una bola de bronce y una rampa de madera. La rampa de madera fue "12 codos de largo, medio codo de ancho y tres traveses de dedo grueso" con una recta, liso, pulido ranura. La ranura se alinea con " pergamino, también lisa y pulida como sea posible ". Y en esta ranura se colocó" una bola de bronce duro, liso y muy redondo ". La rampa se inclina en varios ángulos para frenar la aceleración suficiente para que el tiempo transcurrido se podía medir. La . pelota se le permitió rodar una distancia conocida por la rampa, y se midió el tiempo necesario para que la bola se mueva la distancia conocida El tiempo se midió utilizando un reloj de agua se describe de la siguiente manera:

"Un gran vaso de agua colocada en una posición elevada, a la parte inferior de esta embarcación se suelda un tubo de pequeño diámetro que da un fino chorro de agua, que se recogieron en un vaso pequeño durante el tiempo de cada descenso, ya sea para el conjunto longitud del canal o para una parte de su longitud; el agua así recogida se pesó, después de cada descenso, en un equilibrio muy preciso; las diferencias y las proporciones de estos pesos nos dieron las diferencias y las relaciones de las veces, y esto con tales exactitud que aunque la operación se repitió muchas, muchas veces, no hubo diferencia apreciable en los resultados ".

Galileo encontró que para un objeto en caída libre, la distancia que el objeto ha caído siempre es proporcional al cuadrado del tiempo transcurrido:

Galileo Galilei murió en Arcetri, Italia (cerca de Florencia), el 8 de enero de 1642. Galileo había mostrado que los objetos en caída libre bajo la influencia del campo gravitatorio de la Tierra tienen una aceleración constante, y contemporáneo, Johannes Kepler de Galileo, había demostrado que los planetas seguir trayectorias elípticas bajo la influencia de la masa gravitacional del Sol. Sin embargo, la relación entre el campo gravitacional de Galileo y la masa gravitatoria de Kepler no estaba comprendido en vida de Galileo.

Masa gravitatoria newtoniana

Isaac Newton 1689

Luna de la Tierra		Misa de la Tierra
Semieje mayor	Período orbital sideral
0.002 569 AU	0.074 802 año sideral
La gravedad de la Tierra	Radio de la Tierra
9.806 65 m / s 2	6 375 kilometros

Robert Hooke publicó su concepto de las fuerzas gravitacionales en 1674, afirmando que, todos los órganos Cœlestial de ningún tipo, tienen una atracción o poder gravitar hacia sus propios Centros [y] ellos también atraen a todos los demás Cuerpos Cœlestial que están dentro de la esfera de su actividad . Afirma, además, que la atracción gravitacional aumenta cuánto más cerca del cuerpo obrado en ellos es su propio centro. En una correspondencia de 1679-1680 entre Robert Hooke y Isaac Newton , Hooke conjetura que las fuerzas gravitatorias podrían disminuir de acuerdo con el doble de la distancia entre los dos cuerpos. Hooke instó a Newton, que fue un pionero en el desarrollo del cálculo , para trabajar a través de los detalles matemáticos de las órbitas de Kepler para determinar si la hipótesis de Hooke fue correcta. Las propias investigaciones de Newton verificaron que Hooke era correcta, pero debido a las diferencias personales entre los dos hombres, Newton optó por no revelar esto a Hooke. Isaac Newton mantuvo silencio sobre sus descubrimientos hasta 1684, momento en el que le dijo a un amigo, Edmond Halley , que había resuelto el problema de las órbitas gravitacionales, pero había perdido la solución en su oficina. Después de ser alentado por Halley, Newton decidió desarrollar sus ideas acerca de la gravedad y publicar todos sus hallazgos. En noviembre de 1684, Isaac Newton envió un documento a Edmund Halley, ahora perdido, pero presume que se han titulado De motu corporum en gyrum (en latín significa "En el movimiento de los cuerpos en una órbita"). Halley presentó las conclusiones de Newton a la Real Sociedad de Londres, con la promesa de que una presentación más completa seguiría. Newton más tarde grabó sus ideas en un conjunto de tres libros, titulado Philosophiæ Naturalis Principia Mathematica (latín: "Principios matemáticos de filosofía natural"). El primero fue recibido por la Royal Society el 28 de abril 1685 a 6, el segundo el 2 de marzo 1686-7, y el tercero el 6 de abril 1686-7. La Royal Society publicó colección completa de Newton a su propio costo mayo 1686-7.

Isaac Newton había tendido un puente entre masa gravitacional de Kepler y la aceleración gravitatoria de Galileo, y demostró la siguiente relación:

dondeges la aparente aceleración de un cuerpo a medida que pasa a través de una región del espacio donde existen campos gravitacionales,μes la masa gravitacional (parámetro gravitacional estándar) del cuerpo causando campos gravitacionales, yRes la coordenada radial (la distancia entre el centros de los dos cuerpos).

Al encontrar la relación exacta entre la masa gravitacional de un cuerpo y su campo gravitacional, Newton proporcionó un segundo método para medir la masa gravitatoria. La masa de la Tierra se puede determinar utilizando el método de Kepler (de la órbita de la luna de la Tierra), o puede ser determinada por la medición de la aceleración de la gravedad en la superficie de la Tierra, y multiplicando que por el cuadrado del radio de la Tierra. La masa de la Tierra es de aproximadamente tres millonésimas de la masa del Sol Hasta la fecha, ningún otro método preciso para medir la masa gravitacional ha sido descubierto.

Bala de cañón de Newton

Bala de cañón de Newton era un pensado experimento utilizado para cerrar la brecha entre la aceleración gravitacional de Galileo y las órbitas elípticas de Kepler. Apareció en 1728 el libro de Newton Un Tratado del sistema del mundo . De acuerdo con el concepto de la gravitación de Galileo, una piedra cayó cae con aceleración constante hacia abajo, hacia la Tierra. Sin embargo, Newton explica que cuando se lanza una piedra horizontalmente (es decir, hacia los lados o perpendicular a la gravedad de la Tierra) sigue una trayectoria curva. "Para una piedra proyectada es por la presión de su propio peso forzada fuera de la trayectoria rectilínea, que por la proyección solo debería haber perseguido y hecho para describir una línea curva en el aire; y por medio de esa manera torcida está al fin derribado al suelo. Y cuanto mayor sea la velocidad es con la que se proyecta, más lejos se va antes de que caiga a la Tierra ".

Newton otras razones que si un objeto se "proyecta en una dirección horizontal desde la parte superior de una montaña alta" con la velocidad suficiente, "sería llegar al fin bastante más allá de la circunferencia de la Tierra, y volver a la montaña desde la que se proyecta . "experimento mental de Newton se ilustra en la imagen a la derecha. Un cañón en la cima de una montaña muy alta dispara una bala de cañón en una dirección horizontal. Si la velocidad es baja, simplemente se cae de nuevo en la Tierra (rutas A y B). Sin embargo, si la velocidad es igual o mayor que algún umbral ( velocidad orbital), pero no lo suficientemente alto como para dejar la Tierra por completo ( velocidad de escape, la ruta E), continuará girando alrededor de la Tierra a lo largo de una órbita elíptica (C y D).

Masa gravitatoria universal y la cantidad

Bala de cañón de Newton ilustra la relación entre la masa gravitacional de la Tierra y su campo gravitatorio; sin embargo, un número de otras ambigüedades todavía permanecía. Robert Hooke había afirmado en 1674 que: "todos los cuerpos celestes de ningún tipo, tienen una atracción o poder gravitar hacia sus propios centros", pero Hooke tenía ni explicó por qué esta atracción gravitando era exclusiva de los cuerpos celestes, ni había explicado por qué la atracción fue dirigida hacia el centro de un cuerpo celeste.

Una manzana experimenta campos gravitatorios dirigidas a todas las partes de la Tierra;sin embargo, la suma total de estos muchos campos produce un solo campo gravitacional dirigida hacia el centro de la Tierra

Para responder a estas preguntas, Newton introdujo el concepto totalmente nuevo que la masa gravitacional es "universal": lo que significa que cada objeto tiene masa gravitatoria, y por lo tanto, cada objeto genera un campo gravitatorio. Newton supone además que la fuerza del campo gravitatorio de cada objeto disminuiría según el cuadrado de la distancia a ese objeto. Con estas premisas en mente, Newton calculó cuál sería el campo gravitatorio global si una gran colección de objetos pequeños se formaron en un cuerpo esférico gigante. Newton encontrado que un cuerpo esférico gigante (como la Tierra o Sun, con la densidad más o menos uniforme en cada radio dado), tendría un campo gravitacional, que era proporcional a la masa total del cuerpo, e inversamente proporcional al cuadrado de la distancia a el centro del cuerpo.

Concepto de masa gravitacional universal de Newton se ilustra en la imagen a la izquierda. Cada pieza de la Tierra tiene una masa gravitatoria y cada pieza crea un campo gravitatorio dirigido hacia esa pieza. Sin embargo, el efecto global de estos muchos campos es equivalente a un único campo de gran alcance dirigida hacia el centro de la Tierra. La manzana se comporta como si un solo poderoso campo gravitatorio se acelera hacia el centro de la Tierra.

Concepto de masa de gravitación universal de Newton pone masa gravitatoria en pie de igualdad con los conceptos tradicionales de peso y cantidad. Por ejemplo, los antiguos romanos habían utilizado la semilla de algarrobo como un estándar de peso. Los romanos podían colocar un objeto con un peso desconocido en un lado de una balanza y colocar las semillas de algarrobo en el otro lado de la escala, lo que aumenta el número de semillas hasta que se equilibra la balanza. Si el peso de un objeto es equivalente a 1,728 semillas de algarrobo, a continuación, el objeto se dijo que pesar una libra romana.

Según la teoría de la gravitación universal de Newton, cada semilla de algarrobo produce campos gravitatorios. Por lo tanto, si uno fuera a recoger un inmenso número de semillas de algarrobo y formar con ellos una enorme esfera, entonces el campo gravitatorio de la esfera sería proporcional a la cantidad de semillas de algarrobo en la esfera. Por lo tanto, debería ser teóricamente posible determinar el número exacto de semillas de algarrobo que serían necesarios para producir un campo gravitatorio similar a la de la Tierra o dom Y puesto que las unidades de peso romanos eran todos se define en términos de semillas de algarrobo, a continuación, conocer la Tierra, o "masa de la semilla de algarrobo" de Sun permitiría una para calcular la masa en libras romanas, u onzas romanos, o cualquier otra unidad romana.

Sección de dibujo Vertical de torsión instrumento equilibrio de Cavendish incluyendo el edificio en el que se aloja. Las grandes bolas fueron colgados de un marco para que pudieran ser girados en su posición al lado de las pequeñas bolas por una polea desde fuera. Figura 1 del documento del Cavendish.

Esta posibilidad se extiende más allá de las unidades romanas y la semilla de algarrobo. La libra avoirdupois británica, por ejemplo, fue originalmente definido para ser igual a 7.000 granos de cebada. Por lo tanto, si se pudiera determinar la "masa de granos de cebada" de la Tierra (el número de granos de cebada se requieren para producir un campo gravitatorio similar a la de la Tierra), a continuación, esto permitiría una para calcular la masa de la Tierra en libras avoirdupois. Además, el kilogramo original se define para que sea igual en masa a un litro de agua pura (el kilogramo moderna se define por el hecho por el hombre kilogramo prototipo internacional). Por lo tanto, la masa de la Tierra en kilogramos teóricamente podría ser determinada por averiguar cómo se necesitarían muchos litros de agua pura (o kilogramos prototipo internacional) para producir campos gravitacionales similares a las de la Tierra. De hecho, es una simple cuestión de abstracción para darse cuenta de que cualquier unidad de masa tradicional teóricamente se puede utilizar para medir la masa gravitacional.

Medición de masa gravitatoria en términos de unidades de comunicación tradicionales es simple en principio, pero extremadamente difícil en la práctica. De acuerdo con la teoría de Newton todos los objetos producen campos gravitacionales y es teóricamente posible recoger un inmenso número de objetos pequeños y formar con ellos una enorme esfera de gravitación. Sin embargo, desde un punto de vista práctico, los campos gravitatorios de los objetos pequeños son extremadamente débiles y difíciles de medir. Y si uno fuera a recoger un inmenso número de objetos, la esfera resultante probablemente sería demasiado grande para construir en la superficie de la Tierra, y demasiado caros de construir en el espacio. Libros de Newton sobre la gravitación universal fueron publicados en la década de 1680, pero la primera medición satisfactoria de la masa de la Tierra en términos de unidades de comunicación tradicionales, el experimento de Cavendish, no se produjo hasta 1797, más de cien años después. Cavendish encontró que la densidad de la Tierra era de 5.448 ± 0.033 veces la del agua. A partir de 2009, la masa de la Tierra en kilogramos solamente se sabe que alrededor de cinco dígitos de precisión, mientras que su masa gravitacional es conocido por más de nueve cifras significativas.

Inercial y la masa gravitatoria

Aunque la masa de inercia, masa gravitatoria pasiva y masa gravitacional activa son conceptualmente distintas, ningún experimento ha demostrado siempre sin ambigüedad alguna diferencia entre ellos. En la mecánica clásica , la tercera ley de Newton implica que la masa gravitacional activa y pasiva siempre debe ser idéntico (o al menos proporcional), pero la teoría clásica no ofrece ninguna razón convincente por qué la masa gravitatoria tiene que ser igual a la masa inercial. Eso que hace es simplemente un hecho empírico.

Albert Einstein desarrolló su teoría general de la relatividad de partida desde el supuesto de que esta correspondencia entre inercial y (pasivo) masa gravitatoria no es accidental: que ningún experimento jamás detectar una diferencia entre ellos (la versión débil del principio de equivalencia). Sin embargo, en la teoría resultante, la gravitación no, no es una fuerza y por lo tanto sujetos a la tercera ley de Newton, por lo que "la igualdad de inercia y activa masa gravitacional [...] sigue siendo tan enigmática como siempre ".

Masa inercial

Masa inerciales la masa de un objeto medido por su resistencia a la aceleración.

Para entender lo que es la masa inercial de un cuerpo, se parte de la mecánica clásica y las leyes del movimiento de Newton . Más adelante, veremos cómo se debe modificar la definición clásica de la masa si se tiene en cuenta la teoría de la relatividad especial , que es más precisa que la mecánica clásica. Sin embargo, las implicaciones de la relatividad especial no va a cambiar el sentido de la "masa" de ninguna manera esencial.

De acuerdo conla segunda ley de Newton, decimos que un cuerpo tiene una masamsi, en cualquier instante de tiempo, que obedece a la ecuación de movimiento

donde F es la resultante fuerza actúa sobre el cuerpo y una es la aceleración del centro de la cuerpo de masa. Por el momento, vamos a dejar a un lado la cuestión de lo que significa "fuerza que actúa sobre el cuerpo" en realidad significa.

Esta ecuación ilustra cómo la masa se ​​refiere a la inercia de un cuerpo. Considere dos objetos con diferentes masas. Si aplicamos una fuerza idéntica a cada uno, el objeto con una masa más grande experimentará una aceleración más pequeño, y el objeto con una masa más pequeña experimentará una aceleración más grande. Podríamos decir que la mayor masa ejerce una mayor "resistencia" a la evolución de su estado de movimiento en respuesta a la fuerza.

Sin embargo, esta noción de la aplicación de fuerzas "idénticas" a los diferentes objetos que nos lleva de nuevo al hecho de que en realidad no hemos definido lo que es una fuerza. Podemos dejar de lado esta dificultad con la ayuda de la tercera ley de Newton , que establece que si un objeto ejerce una fuerza sobre un segundo objeto, se experimentará una fuerza igual y opuesta. Para ser precisos, supongamos que tenemos dos objetos X e Y, con constantes masas inerciales m _X y m _Y . Nos aislamos los dos objetos de todas las otras influencias físicas, de modo que las únicas fuerzas presentes son la fuerza ejercida sobre X por Y, que denotamos F _XY , y la fuerza ejercida sobre Y por X, que denotamos F _YX . La segunda ley de Newton establece que

donde un _X y una _Y son las aceleraciones de X e Y, respectivamente. Supongamos que estas aceleraciones son diferentes de cero, de modo que las fuerzas entre los dos objetos son diferentes de cero. Esto ocurre, por ejemplo, si los dos objetos están en el proceso de chocar uno con el otro. La tercera ley de Newton a continuación que

y por lo tanto

Tenga en cuenta que nuestra exigencia de queun _Xno-cero haber asegura que está bien definida la fracción.

Esto es, en principio, cómo íbamos a medir la masa inercial de un objeto. Elegimos un objeto de "referencia" y definir su masa m _Y como (por ejemplo) 1 kilogramo. Entonces podemos medir la masa de cualquier otro objeto en el universo al chocar con el objeto de referencia y medir las aceleraciones.

Masa gravitatoria newtoniana

El concepto newtoniano de la masa gravitatoria descansa sobre La ley de Newton de la gravitación. Supongamos que tenemos dos objetos A y B, separados por una distancia R _{UNA B} . La ley de gravitación establece que si A y B tienen masas gravitacionales M _LA y M _B respectivamente, entonces cada objeto ejerce una fuerza gravitacional sobre el otro, de magnitud

,

dondeGes lo universal constante gravitacional.La declaración anterior puede reformularse de la siguiente manera: siges la magnitud en un lugar determinado en un campo gravitacional, entonces la fuerza de la gravedad sobre un objeto con masa gravitacionalMes

.

Esta es la base por la cual se determinan por masas de pesaje. En simples escalas de primavera, por ejemplo, la fuerza F es proporcional al desplazamiento de la primavera debajo del plato de pesada, según la ley de Hooke, y la balanza se calibra para tomar g en cuenta, lo que la masa M para ser leído fuera. La equilibrio medidas de masa gravitatoria; Sólo la primavera de peso medidas escala.

Equivalencia de las masas inerciales y gravitacionales

La equivalencia de las masas inerciales y gravitacionales se refiere a veces como el "principio de equivalencia de Galilea" o el " principio de equivalencia débil ". La consecuencia más importante de este principio de equivalencia se aplica a caer libremente objetos. Supongamos que tenemos un objeto con inerciales y gravitacionales masas m y M , respectivamente. Si la única fuerza que actúa sobre el objeto viene de un campo gravitatorio g , combinando la segunda ley de Newton y la ley de la gravedad produce la aceleración

Esto dice que la relación de gravitatoria a la masa inercial de cualquier objeto es igual a alguna constante K si y sólo si todos los objetos caen a la misma velocidad en un campo gravitatorio dado. Este fenómeno se conoce como la "universalidad de caída libre". (Además, la constante K se pueden tomar para ser 1 mediante la definición de nuestras unidades apropiadamente.)

Los primeros experimentos que demuestran la universalidad de caída libre se llevaron a cabo por Galileo . Se afirma comúnmente que Galileo obtuvo sus resultados al dejar caer objetos desde la torre inclinada de Pisa , pero esto es muy probablemente apócrifa; En realidad, él realizó sus experimentos con bolas rodando por casi frictionaless planos inclinados para frenar el movimiento y aumentar la precisión de tiempo. Se han realizado experimentos cada vez más precisas, como las realizadas por Loránd Eötvös, mediante el equilibrio del péndulo de torsión, en 1889. A partir de 2008, ninguna desviación de universalidad, y por lo tanto de la equivalencia de Galilea, nunca se ha encontrado, por lo menos a la precisión 10 ^-12 . esfuerzos experimentales más precisos todavía están llevando a cabo.

La universalidad de la caída libre sólo se aplica a sistemas en los que la gravedad es la única fuerza que actúa. Todas las demás fuerzas, especialmente fricción y la resistencia del aire, deben estar ausentes o por lo menos insignificante. Por ejemplo, si un martillo y una pluma se dejan caer desde la misma altura en el aire en la Tierra, la pluma tomará mucho más tiempo en llegar al suelo; la pluma no está realmente en libre -otoño porque la fuerza de resistencia del aire hacia arriba contra la pluma es comparable a la fuerza hacia abajo de la gravedad. Por otro lado, si el experimento se realiza en un vacío, en el que no hay resistencia del aire, el martillo y la pluma debe golpear el suelo exactamente en el mismo tiempo (suponiendo que la aceleración de los dos objetos uno hacia el otro, y de la suelo hacia ambos objetos, por su parte, es insignificante). Esto se puede hacer fácilmente en un laboratorio de la escuela secundaria al dejar caer los objetos en tubos transparentes que tienen el aire eliminado con una bomba de vacío. Es aún más dramática cuando se hace en un ambiente que, naturalmente, tiene un vacío, como David Scott hizo en la superficie de la Luna durante Apolo 15.

Una versión más fuerte del principio de equivalencia, conocido como el principio de equivalencia de Einstein o la fuerte principio de equivalencia , se encuentra en el corazón de la teoría general de la relatividad . Principio de equivalencia de Einstein afirma que dentro suficientemente pequeñas regiones del espacio-tiempo, es imposible distinguir entre una aceleración uniforme y un campo gravitatorio uniforme. Así, la teoría postula que la fuerza que actúa sobre un objeto masivo causado por un campo gravitatorio es el resultado de la tendencia del objeto a moverse en una línea recta (en otras palabras su inercia) y por lo tanto debería ser una función de su masa inercial y la fuerza del campo gravitatorio.

Masa y energía en la relatividad especial

El término masa en relatividad especial por lo general se refiere a la masa en reposo del objeto, que es la masa newtoniana medida por un observador en movimiento junto con el objeto. La masa invariante es otro nombre para la masa en reposo de las partículas individuales. Sin embargo, la masa invariante más general (calculado con una fórmula más complicado) también se puede aplicar a sistemas de partículas en movimiento relativo, y debido a esto, es generalmente reservado para los sistemas que consisten en partículas de alta energía ampliamente separadas. La masa invariante de los sistemas es la misma para todos los observadores y sistemas inerciales, y no puede ser destruida, y por lo tanto se conserva, en tanto que el sistema es cerrado. En este caso, "cierre" implica que un límite idealizada se dibuja alrededor del sistema, y no se permite ninguna masa / energía a través de ella.

En tanto como la energía se conserva en sistemas cerrados en la relatividad, la masa de un sistema es también una cantidad que se conserva: esto significa que no cambia con el tiempo, incluso como algunos tipos de partículas se convierten a otros. Para cualquier observador dado, la masa de cualquier sistema se conserva por separado y no se puede cambiar con el tiempo, al igual que la energía se conserva por separado y no se puede cambiar con el tiempo. La idea popular errónea de que la masa se ​​puede convertir en energía (sin masa) en la relatividad es debido a que algunos de materia partículas pueden en algunos casos ser convertidos a los tipos de energía que no se importan (como la luz, la energía cinética y la energía potencial en magnético, eléctrico, y otros campos). Sin embargo, esto confunde "materia" (una cosa no conservada y mal definida) con la masa (que está bien definido y se conserva). Incluso si no se consideran "materia", todos los tipos de energía aún continúan exhibiendo masa en la relatividad. Por lo tanto, la masa y la energía no cambian en uno otro en la relatividad; más bien, ambos son nombres para la misma cosa, y ni masa ni energía aparecen sin el otro. Partículas "materia" no pueden ser conservados en las reacciones de la relatividad, pero la masa del sistema cerrado siempre es.

Por ejemplo, una bomba nuclear en una caja-fuerte estupendo idealizada, sentado en una escala, sería, en teoría, no muestran cambio en la masa cuando detonó (aunque el interior de la caja se volvería mucho más caliente). En tal sistema, la masa de la caja sería cambiar sólo si la energía se les permitió escapar de la caja como la luz o el calor. Sin embargo, en ese caso, la energía eliminado tomaría su masa asociada a ella. Dejar que el calor fuera de un sistema de este tipo no es más que una manera de quitar la masa. Por lo tanto, la masa, como la energía, no puede ser destruido, pero sólo se movía de un lugar a otro.

En los sistemas consolidados, la energía de enlace debe (a menudo) se restará de la masa del sistema no unido, simplemente porque esta energía tiene masa, y esta masa se ​​resta de la sistema cuando se emite, en el momento que está obligado. Masa no se conserva en este proceso ya que el sistema no está cerrada durante el proceso de unión. Un ejemplo conocido es la energía de enlace de los núcleos atómicos , que aparece como otros tipos de energía (como los rayos gamma) cuando se forman los núcleos, y (después de haber sido emitida) resulta en nucleidos que tienen menos masa que las partículas libres ( nucleones ) de los que se componen.

El término masa relativista se utiliza también, y esto es la cantidad total de energía en un cuerpo o sistema (dividido por c ² ). La masa relativista (de un cuerpo o sistema de cuerpos) incluye una contribución de la energía cinética del cuerpo, y es mayor cuanto más rápido se mueve el cuerpo, por lo que a diferencia de la masa invariante, la masa relativista depende del observador de marco de referencia. Sin embargo, para determinado sola marcos de referencia y para sistemas cerrados, la masa relativista es también una cantidad conservada.

Debido a que la masa relativista es proporcional a la energía, se ha caído en desuso gradualmente entre los físicos. Hay desacuerdo sobre si el concepto sigue siendo pedagógicamente útil.

Misa en la relatividad general

En la relatividad general , el principio de equivalencia es cualquiera de varios conceptos relacionados que se ocupan de la equivalencia de la gravedad y la masa inercial . En el núcleo de esta afirmación es de Albert Einstein idea de que la fuerza gravitatoria tan experimentado a nivel local, mientras que de pie sobre un cuerpo masivo (como la Tierra) es el mismo que el de la fuerza de la pseudo experimentado por un observador en un no- inercial (acelerado) Plazo de referencia.

Sin embargo, resulta que es imposible encontrar una definición general objetiva para el concepto de masa invariante en la relatividad general. En el núcleo del problema es la no linealidad de las ecuaciones de campo de Einstein, que hace que sea imposible escribir la energía del campo gravitacional como parte del tensor de tensión-energía de una manera que es invariante para todos los observadores. Para un observador dado, esto se puede lograr por el pseudotensor Stress-energía-impulso.

Misa en la física cuántica

Enla mecánica clásica, la masa inerte de una partícula aparece en laecuación de Euler-Lagrange como parámetrom,

.

Después de la cuantificación, en sustitución de la posición vectorxcon unafunción de onda, el parámetromaparece en laenergía cinéticadel operador,

.

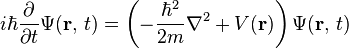En el ostensiblementecovariante (relativista invariante)ecuación de Dirac, y enunidades naturales, esto se convierte en

Cuando la "masa "parámetromes ahora simplemente una constante asociada a lacuántica descrita por la función de onda ψ.

En el Modelo Estándar de la física de partículas como se desarrolla en la década de 1960, no es la propuesta que se plantea este término desde el acoplamiento del campo ψ a un Φ campo adicional, la llamada de la Campo de Higgs. En el caso de los fermiones, los resultados del mecanismo de Higgs en ​​el sustitución del término m ψ en el Lagrangiano con 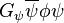. Esto cambia el explanandum del valor de la masa de cada partícula elemental con el valor de la acoplamientos desconocido G _ψ . El descubrimiento de una masiva Higgs Higgs sería considerado como una fuerte confirmación de esta teoría. Pero hay evidencia indirecta de la realidad de la simetría electrodébil romper como describe el mecanismo de Higgs, y la no existencia del bosón de Higgs indicaría una " Higgsless "descripción de este mecanismo.

Origen de la masa

En la física teórica, un mecanismo de generación de masa es una teoría que trata de explicar el origen de la masa de las leyes más fundamentales de la física . Hasta la fecha, se han propuesto una serie de diferentes modelos que abogan por diferentes puntos de vista en el origen de la masa. El problema se complica por el hecho de que la noción de masa está fuertemente relacionada con la interacción gravitatoria sino una teoría de este último aún no ha sido reconciliado con el modelo actualmente popular de la física de partículas , conocido como el Modelo Estándar .