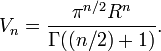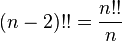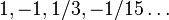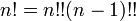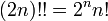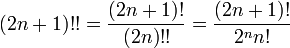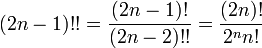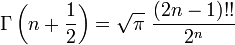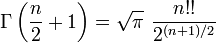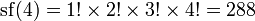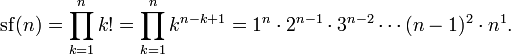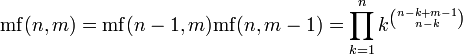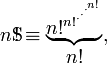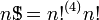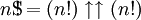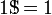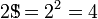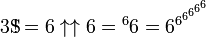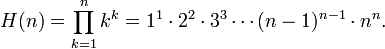Factorial
Acerca de este escuelas selección Wikipedia
SOS Children, una organización benéfica educación , organizó esta selección. Madres SOS cada aspecto después de un una familia de niños apadrinados .
 |  |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 15 | 1307674368000 |
| 20 | 2432902008176640000 |
| 25 | 15511210043330985984000000 |
| 50 | 3.04140932 ... × 10 64 |
| 70 | 1.19785717 ... × 10 100 |
| 450 | 1.73336873 ... × 10 1000 |
| 3249 | 6.41233768 ... × 10 10 000 |
| 25206 | 1.205703438 ... × 10 100000 |
| 47176 | 8,4485731495 ... × 10 200001 |
| 100000 | 2,8242294079 ... × 10 456573 |
En matemáticas , el factorial de un no negativo entero n, denotado por n!, es el producto de todos los enteros positivos menores o iguales a n. Por ejemplo,
- y
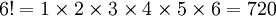
donde n! representa n factorial. La notación n! fue presentado por Cristiano Kramp en 1808 .
Definición
La función factorial se define formalmente por
La definición anterior incorpora la instancia
como una instancia del hecho de que la producto de ningún número en absoluto es 1. Este hecho para factoriales es útil, porque
- la relación recursiva
 trabaja para
trabaja para  ;
; - esta definición hace que muchas identidades en la combinatoria válidos para cero tamaños.
- En particular, el número de combinaciones o permutaciones de un conjunto vacío es, simplemente, 1.
Aplicaciones
- Los factoriales se utilizan en la combinatoria . Por ejemplo, hay
 diferentes formas de organización de n objetos distintos en una secuencia. (Los arreglos se llaman permutaciones .) Y el número de maneras que uno puede elegir k objetos de entre un conjunto dado de n objetos (el número de combinaciones), está dado por el llamado coeficiente binomial
diferentes formas de organización de n objetos distintos en una secuencia. (Los arreglos se llaman permutaciones .) Y el número de maneras que uno puede elegir k objetos de entre un conjunto dado de n objetos (el número de combinaciones), está dado por el llamado coeficiente binomial
- En permutaciones , si
 los objetos pueden ser elegidos de un total de n objetos y dispuestos de diferentes maneras, donde r ≤ n, entonces el número total de permutaciones distintas viene dada por:
los objetos pueden ser elegidos de un total de n objetos y dispuestos de diferentes maneras, donde r ≤ n, entonces el número total de permutaciones distintas viene dada por:
- Los factoriales también a su vez en el cálculo . Por ejemplo, el teorema de Taylor expresa una función f (x) como una serie de potencias en x, básicamente debido a que el n-ésimo derivado de x n es n!.
- Factoriales también se utilizan ampliamente en la teoría de probabilidad .
- Factoriales se utilizan a menudo como un ejemplo sencillo, junto con los números de Fibonacci , al enseñar recursividad en ciencias de la computación porque satisfacen la siguiente relación recursiva (si n ≥ 1):
Teoría de los números
Los factoriales tienen muchas aplicaciones en la teoría de números . En particular, n! es necesariamente divisible por todos los números primos hasta e incluyendo n. Como consecuencia, n> 5 es una número compuesto si y solo si
Un resultado más fuerte es El teorema de Wilson, que establece que
si y sólo si p es primo.
Adrien-Marie Legendre encontró que la multiplicidad del primo p que ocurre en la descomposición en factores primos de n! se puede expresar exactamente como
que es finita ya que la la función del suelo elimina todo 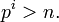
La única factorial que también es un número primo es 2, pero hay muchos primos de la forma 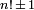 , Llamado primos factoriales.
, Llamado primos factoriales.
Todos los factoriales mayor que 0! y 1! son incluso, como lo son todos los múltiplos de 2.
Tasa de crecimiento
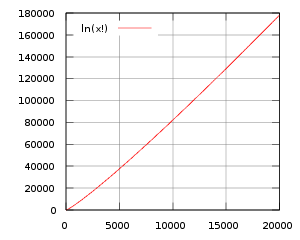
Como n crece, el factorial n! se vuelve más grande que todos los polinomios y funciones exponenciales en n.
Cuando n es grande, n! se puede estimar con bastante precisión utilizando Aproximación de Stirling:
Una versión débil que puede ser fácilmente demostrado con inducción matemática es
El logaritmo de la factorial se puede utilizar para calcular el número de dígitos en una base dada el factorial de un número dado tomará. Satisface la identidad:
Tenga en cuenta que esta función, si graficado, es de aproximadamente lineal, para valores pequeños; pero el factor 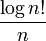 , Y por lo tanto la pendiente de la gráfica, crece arbitrariamente grande, aunque muy lentamente. La gráfica de
, Y por lo tanto la pendiente de la gráfica, crece arbitrariamente grande, aunque muy lentamente. La gráfica de 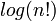 para
para  entre 0 y 20000 se muestra en la figura de la derecha.
entre 0 y 20000 se muestra en la figura de la derecha.
Una aproximación simple para
basado en Aproximación de Stirling es
Una mejor aproximación para
fue dada por Srinivasa Ramanujan:
Uno puede ver de esto que
es Ο (n log n). Este resultado desempeña un papel clave en el análisis de la complejidad computacional de algoritmos de clasificación (ver comparación de orden).
Cálculo
El valor de  puede ser calculado por la multiplicación repetida si
puede ser calculado por la multiplicación repetida si  no es demasiado grande. El mayor factorial que la mayoría de las calculadoras puede manejar es de 69 !, porque el 70! > 10 100 (excepto para la mayoría de las calculadoras HP que puede manejar 253! Como su exponente puede ser de hasta 499). La calculadora se ve en Mac OS X, Microsoft Excel y Google calculadora puede manejar factoriales hasta 170 !, que es el más grande factorial menos de 2 1024 (10 100 en hexadecimal ) y corresponde a un número entero de 1024 bits. Los valores de 12! y 20! son los mayores factoriales, que pueden almacenarse en, respectivamente, los números enteros de 32 bits y 64 bits de uso común en los ordenadores personales. En la práctica, la mayoría de las aplicaciones de software se computar estos pequeños factoriales por la multiplicación directa o tabla de búsqueda. Los valores más altos a menudo se aproximan en términos de estimaciones de punto flotante de la Función gamma, generalmente con La fórmula de Stirling.
no es demasiado grande. El mayor factorial que la mayoría de las calculadoras puede manejar es de 69 !, porque el 70! > 10 100 (excepto para la mayoría de las calculadoras HP que puede manejar 253! Como su exponente puede ser de hasta 499). La calculadora se ve en Mac OS X, Microsoft Excel y Google calculadora puede manejar factoriales hasta 170 !, que es el más grande factorial menos de 2 1024 (10 100 en hexadecimal ) y corresponde a un número entero de 1024 bits. Los valores de 12! y 20! son los mayores factoriales, que pueden almacenarse en, respectivamente, los números enteros de 32 bits y 64 bits de uso común en los ordenadores personales. En la práctica, la mayoría de las aplicaciones de software se computar estos pequeños factoriales por la multiplicación directa o tabla de búsqueda. Los valores más altos a menudo se aproximan en términos de estimaciones de punto flotante de la Función gamma, generalmente con La fórmula de Stirling.
Por número teórico y combinatorias cálculos, muy grandes factoriales exactas son a menudo necesarios. Factoriales bignum se pueden calcular mediante la multiplicación directa, pero la multiplicación de la secuencia de 1 × 2 × ... × n de abajo hacia arriba (o de arriba hacia abajo) es ineficiente; es mejor para dividir recursivamente la secuencia de modo que el tamaño de cada subproducto se minimiza.
El asintóticamente-mejor eficiencia se obtiene calculando n! desde su primer factorización. Como se documenta en Peter Borwein, factorización prima permite  computado de tiempo O (n (log n log log n) 2), a condición de que un rápido se utiliza el algoritmo de multiplicación (por ejemplo, el Schönhage-Strassen algoritmo). Peter Luschny presenta código fuente y los puntos de referencia para varios algoritmos factoriales eficientes, con o sin el uso de una tamiz de primera.
computado de tiempo O (n (log n log log n) 2), a condición de que un rápido se utiliza el algoritmo de multiplicación (por ejemplo, el Schönhage-Strassen algoritmo). Peter Luschny presenta código fuente y los puntos de referencia para varios algoritmos factoriales eficientes, con o sin el uso de una tamiz de primera.
La función gamma

La función factorial también puede ser definido por los valores no enteros, pero esto requiere más herramientas avanzadas de análisis matemático . La función que "rellena" los valores de la factorial entre los números enteros se llama Función Gamma, denotado 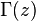 para los números enteros Z no menos de 1, definido por
para los números enteros Z no menos de 1, definido por
De Euler fórmula original para la función Gamma fue
La función Gamma se relaciona con los factoriales de que satisface una relación recursiva similar:
Junto con  esto produce la ecuación para cualquier número entero no negativo
esto produce la ecuación para cualquier número entero no negativo  :
:
Según el valor de la función Gamma de 1.2, el ejemplo concreto de factoriales semienteros se resolvieron
Por ejemplo
La función gamma en realidad está definida para todos los números complejos  a excepción de los números enteros no positivos
a excepción de los números enteros no positivos 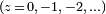 . Se piensa a menudo como una generalización de la función factorial para el dominio complejo, que se justifica por las siguientes razones:
. Se piensa a menudo como una generalización de la función factorial para el dominio complejo, que se justifica por las siguientes razones:
- Significado compartido. La definición canónica de la función factorial comparte la misma relación recursiva con la función Gamma.
- Contexto. La función Gamma se utiliza generalmente en un contexto similar a la de los factoriales (pero, por supuesto, en los que un dominio más general es de interés).
- Singularidad ( Bohr-Mollerup teorema). La función gamma es la única función que satisface la relación recursiva antes mencionado para el dominio de los números complejos, se meromórfica, y es log-convexa en el eje real positivo. Es decir, es la única función suave, log-convexa que podría ser una generalización de la función factorial a todos los números complejos.
Euler también desarrolló una aproximación producto convergente para los factoriales no enteros, los cuales se pueden ver como equivalente a la fórmula de la función gamma encima:
También se puede escribir como a continuación:
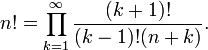
El producto converge rápidamente para valores pequeños de n.
Aplicaciones de la función gamma
- El volumen de un n - dimensional hiperesfera es
Productos factoriales similares
Hay varias otras secuencias de números enteros similares a la factorial que se utilizan en las matemáticas:
Primorial
La primorial (secuencia A002110 en OEIS ) es similar a la factorial, pero con el producto tomarse sólo a través de los números primos .
Doble factorial
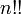 denota el doble factorial de
denota el doble factorial de  y se define de forma recursiva por
y se define de forma recursiva por
Por ejemplo, 8 !! = 2 · 4 · 6 · 8 = 384 y 9 !! = 1 · 3 · 5 · 7 · 9 = 945. La secuencia de dobles factoriales (secuencia A006882 en OEIS ) para 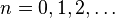 comienza como
comienza como
- 1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, ...
La definición anterior se puede utilizar para definir dobles factoriales de números negativos:
La secuencia de dobles factoriales para 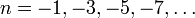 comienza como
comienza como
mientras que el doble factorial de los enteros negativos es infinito.
Algunas identidades implican dobles factoriales son:
donde 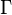 es el Función gamma. La última ecuación anterior se puede utilizar para definir el doble factorial como una función de cualquier número complejo
es el Función gamma. La última ecuación anterior se puede utilizar para definir el doble factorial como una función de cualquier número complejo 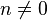 , Así como la función gamma generaliza la función factorial. Hay que tener cuidado de no interpretar
, Así como la función gamma generaliza la función factorial. Hay que tener cuidado de no interpretar 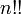 como el factorial de
como el factorial de  , Que se escribiría
, Que se escribiría 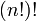 y es un número mucho más grande (por
y es un número mucho más grande (por  ).
).
Multifactoriales
Una notación relacionada común es usar múltiples puntos de exclamación para denotar una multifactorial, el producto de los números enteros en pasos de dos ( 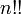 ), Tres (
), Tres ( 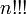 ), O más. El factorial doble es la variante más utilizada, pero se puede definir de manera similar la triple factorial (
), O más. El factorial doble es la variante más utilizada, pero se puede definir de manera similar la triple factorial ( 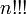 ) Etcétera. En general, la k-ésima factorial, denotado por
) Etcétera. En general, la k-ésima factorial, denotado por 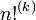 , Se define de forma recursiva como
, Se define de forma recursiva como
Algunos matemáticos han sugerido una notación alternativa de 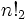 para el doble factorial y de manera similar
para el doble factorial y de manera similar  para otros multifactoriales, pero esto no ha entrado en uso general.
para otros multifactoriales, pero esto no ha entrado en uso general.
Factorial Cuádruple
La factorial cuádruple, sin embargo, no es una multifactorial; Se trata de un número mucho mayor dado por 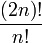 .
.
Superfactorials
Neil Sloane y Simon Plouffe define la superfactorial en 1995 como el producto de la primera  factoriales. Así que la superfactorial de 4 es
factoriales. Así que la superfactorial de 4 es
En general
La secuencia de superfactorials comienza (de  ) Como
) Como
- 1, 1, 2, 12, 288, 34 560, 24883200, ... (secuencia A000178 en OEIS )
Esta idea fue desarrollada en 2000 por Henry Bottomley a la superduperfactorial como el producto de la primera  superfactorials, a partir (de
superfactorials, a partir (de  ) Como
) Como
- 1, 1, 2, 24, 6912, 238 878 720, 5944066965504000, ... (secuencia A055462 en OEIS )
y por lo tanto recursivamente a cualquier factorial de varios niveles donde el m º factorial -nivel de  es el producto de la primera
es el producto de la primera 
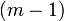 factoriales -Nivel th, es decir,
factoriales -Nivel th, es decir,
donde  para
para  y
y 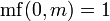 .
.
Superfactorials (definición alternativa)
Clifford Pickover en sus 1.995 Keys libro al Infinito define la superfactorial de  como
como
o como,
donde el (4) notación denota la hyper4 operador, o el uso de Flecha arriba notación de Knuth,
Esta secuencia de superfactorials comienza:
Hyperfactorials
De vez en cuando la hyperfactorial de  se considera. Está escrito como
se considera. Está escrito como 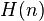 y definido por
y definido por
Para n = 1, 2, 3, 4, ... los valores h (n) son 1, 4, 108, 27648, ... (secuencia A002109 en OEIS ).
La función hyperfactorial es similar a la factorial, pero produce números más grandes. La tasa de crecimiento de esta función, sin embargo, no es mucho más grande que un factorial regular. Sin embargo, H (14) = 1,85 × 10 ... 99 ya es casi igual a una googol, y H (15) = 8,09 × 10 ... 116 es casi de la misma magnitud que el Número Shannon, el número teórico de posibles partidas de ajedrez.
La función hyperfactorial puede generalizarse a los números complejos de una manera similar a la función factorial. La función resultante se llama K-función.
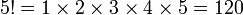
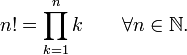
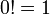
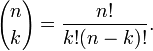

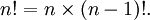
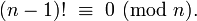
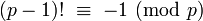
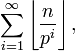
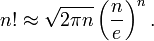
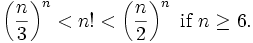
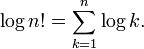
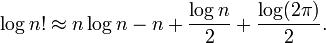
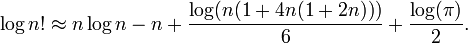
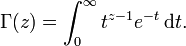
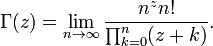
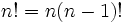
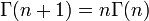
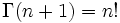
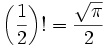
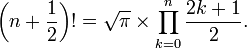
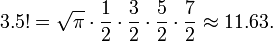
![n! \ Aprox \ left [\ left (\ frac {2} {1} \ right) ^ n \ frac {1} {n + 1} \ right] \ left [\ left (\ frac {3} {2} \ right ) ^ n \ frac {2} {n + 2} \ right] \ left [\ left (\ frac {4} {3} \ right) ^ n \ frac {3} {n + 3} \ right] \ dots](../../images/183/18356.png)