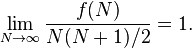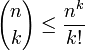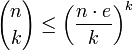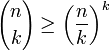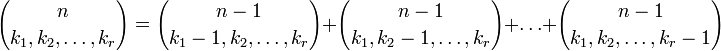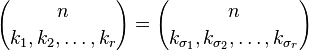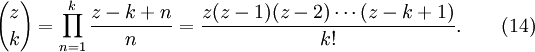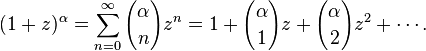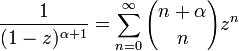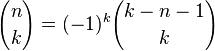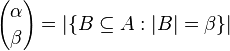Coeficiente binomial
Sabías ...
Esta selección se hace para las escuelas por caridad para niños leer más . SOS Children es la caridad más grande del mundo dando huérfanos y abandonados los niños la oportunidad de la vida familiar.
En matemáticas , en particular en la combinatoria , un coeficiente binomial es una coeficiente de cualquiera de los términos en la expansión de la binomio (x + y) n. Coloquialmente dado, decir que hay n pizzas para elegir, si se quiere hornear una pizza con k exactamente coberturas diferentes, entonces el coeficiente binomial expresa cómo son posibles muchos tipos diferentes de tales k pizzas -topping.
Definición
Dado un número entero no negativo n y k un número entero, el coeficiente binomial se define como el número natural
y
donde n! denota el factorial de n.
De acuerdo a Nicholas J. Higham, el  notación fue introducido por Albert von Ettinghausen en 1826 , aunque estas cifras ya eran conocidos siglos antes (ver el triángulo de Pascal ). Notaciones alternativos incluyen C (n, k), k o n C
notación fue introducido por Albert von Ettinghausen en 1826 , aunque estas cifras ya eran conocidos siglos antes (ver el triángulo de Pascal ). Notaciones alternativos incluyen C (n, k), k o n C  , En todos los cuales el C significa combinación o elegir. De hecho, otro nombre para el coeficiente binomial es elegir la función, y el coeficiente binomial de n y k menudo se lee como "n elegir k".
, En todos los cuales el C significa combinación o elegir. De hecho, otro nombre para el coeficiente binomial es elegir la función, y el coeficiente binomial de n y k menudo se lee como "n elegir k".
Los coeficientes binomiales son la coeficientes en la expansión de la binomial (x + y) n (de ahí el nombre):
Esto se generaliza por el teorema binomial, lo que permite el exponente n sea negativo o un número no entero. Ver el artículo sobre combinación.
Interpretación combinatoria
La importancia de los coeficientes de dos términos (y la motivación para el nombre alternativo "elegir") radica en el hecho de que 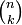 es el número de formas en que k objetos se pueden elegir de entre n objetos, sin importar el orden. Más formalmente,
es el número de formas en que k objetos se pueden elegir de entre n objetos, sin importar el orden. Más formalmente,
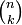 es el número de subconjuntos k -element de un conjunto de n -element.
es el número de subconjuntos k -element de un conjunto de n -element. 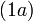
De hecho, esta propiedad se elige a menudo como una definición alternativa del coeficiente binomial, ya que a partir de (1a) se puede derivar (1) como corolario de un sencillo prueba combinatoria. Para una demostración coloquial, tenga en cuenta que en la fórmula
el numerador indica el número de maneras de llenar las ranuras k utilizando las opciones de N, donde las ranuras se pueden distinguir unos de otros. Así, una pizza con setas añadidos antes de pollo se considera que es diferente de una pizza con pollo añade antes de setas. El denominador elimina estas repeticiones porque si las ranuras k son indistinguibles, entonces todos los k! formas de organización de ellos se consideran idénticos.
En el contexto de las ciencias de la computación, sino que también ayuda a ver 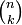 como el número de cadenas que consta de unos y ceros con los k y n - k ceros. Para cada subconjunto k -element, K, de un conjunto de n -element, N, el función indicadora, 1 K: N -> {0,1}, donde 1 K (x) = 1 cuando x en K y 0 en caso contrario, produce una secuencia de bits única de longitud n con exactamente los k por la alimentación de 1 K con el n elementos en un orden específico.
como el número de cadenas que consta de unos y ceros con los k y n - k ceros. Para cada subconjunto k -element, K, de un conjunto de n -element, N, el función indicadora, 1 K: N -> {0,1}, donde 1 K (x) = 1 cuando x en K y 0 en caso contrario, produce una secuencia de bits única de longitud n con exactamente los k por la alimentación de 1 K con el n elementos en un orden específico.
Ejemplo
El cálculo del coeficiente binomial está convenientemente dispuesto de esta manera: ((((5/1) · 6) / 2) · 7) / 3, alternativamente dividiendo y multiplicando con el aumento de números enteros. Cada división produce un resultado entero que es en sí misma un coeficiente binomial.
Derivación de la expansión binomial
Para exponente 1, (x + y) es 1 x + y. Para exponente 2, (x + y) es 2 (x + y) (x + y), que forma términos de la siguiente manera. Las primeras ofertas de factores sea un X o un Y; lo mismo para el segundo factor. Por lo tanto, para formar x 2, la única posibilidad es elegir x de ambos factores; Asimismo, para y 2. Sin embargo, el término xy puede estar formado por x de la primera y de la segunda y factor de, o Y de la primera y de la segunda x factor de; por lo tanto, adquiere un coeficiente de 2. Procedimiento para exponente 3, (x + y) se reduce a 3 (x + y) 2 (x + y), donde ya sabemos que (x + y) 2 = x 2 2 xy + y 2, dando una expansión inicial de (x + y) (x 2 2 xy + y 2). Una vez más, los extremos 3 x e y 3 se presentan de una manera única. Sin embargo, el plazo y x 2 es ya sea 2 xy veces x o x 2 y veces, para un coeficiente de 3; Asimismo xy 2 surge de dos maneras, la suma de los coeficientes 1 y 2 para dar 3.
Esto sugiere una inducción. Así, para exponente n, cada término tiene grado total (suma de los exponentes) n, con n - k factores de x y k factores de y. Si k es 0 ó n, surge el término de una sola manera, y obtenemos los términos x n y y n. Si k no es ni 0 ni n, entonces surge el término de dos maneras, a partir de x NK-1 y k × x y x de nk y k-1 × Y. Por ejemplo, x 2 y 2 es dos veces xy 2 x y x 2 y tiempos de y, por tanto, su coeficiente es 3 (el coeficiente de xy 2) + 3 (el coeficiente de x 2 y). Este es el origen del triángulo de Pascal, se discute a continuación.
Otra perspectiva es que para formar x n - k y k de n factores de (x + y), debemos elegir y de k de los factores y x del resto. Para contar las posibilidades, considere todos los n! permutaciones de los factores. Represente cada permutación como una lista barajado de los números del 1 al n. Seleccione una x de la primera n - k factores enumerados, y una y de los factores k restantes; de esta manera cada permutación contribuye a la expresión x n - k y k. Por ejemplo, la lista <4,1, 2,3> x selecciona de factores 4 y 1, y selecciona y de factores 2 y 3, como una forma para formar el término x 2 y 2.
- (X + 1 y) (x + 2 y) (x + 3 y) (x + 4 y)
Pero la lista distinta <1,4, 3,2> hace exactamente la misma selección; la fórmula coeficiente binomial debe eliminar esta redundancia. El n - k factores para tener x (n - k)! permutaciones, y los factores k para Y tienen K! permutaciones. Por lo tanto n /! (N - k) k! es el número de formas distintas para formar realmente el término x n - k y k.
Una explicación más simple sigue: Uno puede elegir un elemento aleatorio de  exactamente
exactamente  maneras, un segundo elemento aleatorio en
maneras, un segundo elemento aleatorio en 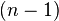 maneras, y así sucesivamente. Por lo tanto,
maneras, y así sucesivamente. Por lo tanto,  elementos de poder elegir de n en
elementos de poder elegir de n en 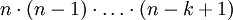 maneras. En este cálculo, sin embargo, se produce cada selección independiente del orden
maneras. En este cálculo, sin embargo, se produce cada selección independiente del orden 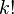 veces, como una lista de
veces, como una lista de  elementos pueden ser permutadas de muchas maneras. Así eq. (1) se obtiene.
elementos pueden ser permutadas de muchas maneras. Así eq. (1) se obtiene.
El triángulo de Pascal
Regla de Pascal es la importante relación de recurrencia
que sigue directamente de la definición:
La relación de recurrencia sólo probado puede ser usado para probar por inducción matemática que C (n, k) es un número natural para todo n y k, un hecho que no es inmediatamente evidente a partir de la definición.
Regla de Pascal también da lugar a triángulo de Pascal :
0: 1 1: 1 1 2: 1 2 1 3: 1 3 3 1 4: 1 4 6 4 1 5: 1 5 10 10 5 1 6: 1 6 15 20 15 6 1 7: 1 7 21 35 35 21 7 1 8: 1 8 28 56 70 56 28 8 1
El número de fila n contiene los números C (n, k) para k = 0, ..., n. Se construye a partir de los en el exterior y luego siempre la adición de dos números adyacentes y escribir la suma directamente debajo. Este método permite el cálculo rápido de los coeficientes binomiales sin la necesidad de fracciones o multiplicaciones. Por ejemplo, al observar la fila número 5 del triángulo, se puede leer rápidamente de que
- (X + y) = 1 5 x 5 x 5 + 4 y + 10 x 3 y 2 + 10 x 2 y 3 + 5 x y 4 + 1 y 5.
Las diferencias entre los elementos en otras diagonales son los elementos de la diagonal anterior, como consecuencia de la relación de recurrencia (3) anterior.
En el tratado 1303 AD Espejo precioso de los Cuatro Elementos, Zhu Shijie mencionó el triángulo como un método antiguo para la evaluación de coeficientes de dos términos que indican que el método era conocido Matemáticos chinos cinco siglos antes de Pascal .
Combinatoria y estadísticas
Coeficientes binomiales son de importancia en la combinatoria , ya que proporcionan fórmulas listas para ciertos problemas de conteo frecuente:
- Cada conjunto con n elementos tiene
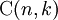 diferentes subconjuntos tener k elementos cada uno (estos son llamados k -conjuntos compuestos).
diferentes subconjuntos tener k elementos cada uno (estos son llamados k -conjuntos compuestos). - El número de cadenas de longitud n que contienen los k y n - k ceros es
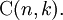
- Hay
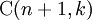 cadenas que consta de los k y n ceros tales que no hay dos son adyacentes.
cadenas que consta de los k y n ceros tales que no hay dos son adyacentes. - El número de secuencias que consta de n números naturales cuya suma es igual a k es
 ; este es también el número de maneras para elegir k elementos de un conjunto de n si se permiten repeticiones.
; este es también el número de maneras para elegir k elementos de un conjunto de n si se permiten repeticiones. - La Números catalanes tienen una fórmula fácil que implica coeficientes de dos términos; que pueden ser utilizados para contar las diversas estructuras, tales como árboles y expresiones entre paréntesis.
Los coeficientes binomiales también se producen en la fórmula para la distribución binomial en estadísticas y en la fórmula para una Curva de Bézier.
Las fórmulas que implican coeficientes binomiales
Uno tiene que
Esto se deduce inmediatamente de la definición o se puede ver desde la expansión (2) mediante el uso de (x + y) n = (y + x) n, y se refleja en la "simetría" numérica de triángulo de Pascal .
Otra fórmula es
se obtiene de expansión (2) usando x = y = 1. Esto es equivalente a decir que los elementos en una fila del triángulo de Pascal siempre se suman a dos elevado a una potencia entera. Una prueba combinatoria de este hecho se da contando subconjuntos de tamaño 0, tamaño 1, tamaño 2, y así sucesivamente hasta el tamaño n de un conjunto S de n elementos. Desde contamos el número de subconjuntos de tamaño i para 0 ≤ i ≤ n, esta suma debe ser igual al número de subconjuntos de S, que se sabe que es 2 n.
La fórmula
se sigue de expansión (2), después de la diferenciación con respecto a X o Y y luego sustituyendo x = y = 1.
La identidad de Vandermonde
se encuentra mediante la expansión de (1+ x) m (1+ x) nm = (x 1+) n con (2). Como C (n, k) es cero si k> n, la suma es finita para número entero n y m. La ecuación (7a) generaliza la ecuación (3). Se mantiene para arbitraria, valores complejos  y
y  , La Identidad Chu-Vandermonde.
, La Identidad Chu-Vandermonde.
Una fórmula relacionada es
Mientras que la ecuación (7a) es verdadera para todos los valores de m, la ecuación (7b) es verdadera para todos los valores de j.
De expansión (7a) usando n = 2 m, k = m, y (4), se encuentra
Denotemos por F (n + 1) los números de Fibonacci . Obtenemos una fórmula sobre las diagonales del triángulo de Pascal
Esto puede ser probado por inducción usando (3).
También usando (3) y la inducción, se puede demostrar que
Una vez más por (3) y la inducción, se puede demostrar que para k = 0, ..., n - 1
así como
que en sí es un caso especial de la consecuencia de que para cualquier entero a = 1, ..., n - 1,
que puede ser demostrado mediante la diferenciación (2) un par de veces y ajuste x = -1 ey = 1.
Identidades combinatorias que implican coeficientes binomiales
Presentamos algunas identidades que tienen pruebas combinatorias. Tenemos, por ejemplo,
para 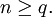 La prueba combinatoria es como sigue: el lado izquierdo cuenta el número de maneras de seleccionar un subconjunto de
La prueba combinatoria es como sigue: el lado izquierdo cuenta el número de maneras de seleccionar un subconjunto de ![[N]](../../images/197/19706.png) de por lo menos q elementos, y que marcan elementos q entre los seleccionados. El lado derecho cuenta con el mismo parámetro, porque hay
de por lo menos q elementos, y que marcan elementos q entre los seleccionados. El lado derecho cuenta con el mismo parámetro, porque hay  maneras de elegir un conjunto de marcas q y ocurrir en todos los subconjuntos que contienen, además, algún subconjunto de los elementos restantes, de los cuales hay
maneras de elegir un conjunto de marcas q y ocurrir en todos los subconjuntos que contienen, además, algún subconjunto de los elementos restantes, de los cuales hay  Esto reduce a (6) cuando
Esto reduce a (6) cuando 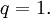
La identidad (8) también tiene una prueba combinatoria. La identidad lee
Suponga que tiene  cuadrados vacíos dispuestos en una fila y que desea marcar (seleccionar) n de ellos. Hay
cuadrados vacíos dispuestos en una fila y que desea marcar (seleccionar) n de ellos. Hay 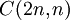 maneras de hacer esto. Por otro lado, es posible elegir sus n plazas seleccionando k cuadrados de los primeros n y
maneras de hacer esto. Por otro lado, es posible elegir sus n plazas seleccionando k cuadrados de los primeros n y  cuadrados de los n restantes plazas. Esto da
cuadrados de los n restantes plazas. Esto da
Ahora aplique (4) para obtener el resultado.
Funciones generadoras
Si no sabemos sobre los coeficientes binomiales podríamos derivar usando el caso del etiquetado Teorema Fundamental del Combinatoria Enumeración. Esto se hace definiendo  siendo el número de formas de particionamiento
siendo el número de formas de particionamiento ![[N]](../../images/197/19706.png) en dos subconjuntos, el primero de los cuales tiene el tamaño k. Estas particiones forman una clase de combinación con la especificación
en dos subconjuntos, el primero de los cuales tiene el tamaño k. Estas particiones forman una clase de combinación con la especificación
Por lo tanto la exponencial la generación de la función B de la función suma de los coeficientes binomiales está dada por
Esto produce inmediatamente
como se esperaba. Marcamos el primer subconjunto con  con el fin de obtener los coeficientes binomiales a sí mismos, dando
con el fin de obtener los coeficientes binomiales a sí mismos, dando
Esto produce la función generatriz bivariante
La extracción de coeficientes, encontramos que
o
de nuevo como se esperaba. Esta derivación se incluye aquí porque se asemeja mucho a la de la Stirling números de la primera y segunda clase, y por lo tanto se presta apoyo a la notación de estilo binomial que se utiliza para estos números.
Divisores de coeficientes binomiales
Los principales divisores de C (n, k) se pueden interpretar como sigue: si p es un número primo p y r es la mayor potencia de p que divide C (n, k), entonces r es igual al número de los números naturales j tal que el parte fraccionaria de k / p j es más grande que la parte fraccionaria de n / p j. En particular, C (n, k) es siempre divisible por n / mcd (n, k).
Un resultado algo sorprendente por David Singmaster (1974) es que cualquier divide enteros casi todos los coeficientes binomiales. Más precisamente, fijar un número entero d y dejar que f (N) denotan el número de coeficientes binomiales C (n, k) con n <N tal que d divide C (n, k). Entonces
Dado que el número de coeficientes binomiales C (n, k) con n <N es N (N 1) / 2, esto implica que la densidad de los coeficientes binomiales divisibles por d va a 1.
Límites para los coeficientes binomiales
Los siguientes límites para C (n, k) sostienen:
Las generalizaciones
Generalización a multinomios
Coeficientes binomiales pueden generalizarse a coeficientes multinomiales. Ellos se definen como el número:
donde
Mientras que los coeficientes binomiales representan los coeficientes de (x + y) n, los coeficientes multinomiales representan los coeficientes del polinomio
- (X 1 + x 2 + ... + x r) n.
Ver teorema multinomial. El caso k = 2 da coeficientes de dos términos:
La interpretación combinatoria de coeficientes multinomiales es la distribución de n elementos distinguibles más de R contenedores (distinguibles), cada uno conteniendo exactamente k i elementos, donde i es el índice del recipiente.
Coeficientes multinomiales tienen muchas propiedades similares a las de los coeficientes binomiales, por ejemplo la relación de recurrencia:
y la simetría:
donde 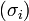 es una permutación de (1,2, ..., r).
es una permutación de (1,2, ..., r).
La generalización a enteros negativos
Si  , A continuación,
, A continuación, 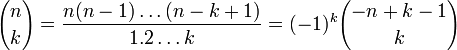 se extiende a todos
se extiende a todos  .
.
El coeficiente binomial se extiende a  vía
vía
Nótese en particular, que
Esto da lugar a la Pascal hexágono o Pascal molino de viento.
- Hilton, Holton y Pedersen (1997). Reflexiones matemáticos. Springer. ISBN 0-387-94770-1.
Generalización al argumento real y complejo
El coeficiente binomial  se puede definir para cualquier número complejo z y cualquier número natural k como sigue:
se puede definir para cualquier número complejo z y cualquier número natural k como sigue:
Esta generalización se conoce como el coeficiente binomial generalizado y se utiliza en la formulación de la teorema del binomio y satisface las propiedades (3) y (7).
Para k fija, la expresión 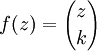 es un polinomio en z de grado k con racionales coeficientes.
es un polinomio en z de grado k con racionales coeficientes.
f (z) es el polinomio único de grado k satisfacer
- f (0) = f (1) = ... = f (k - 1) = 0 y f (k) = 1.
Cualquier polinomio p (z) de grado d se puede escribir en la forma
Esto es importante en la teoría de la ecuaciones en diferencias y diferencias finitas, y pueden ser vistos como un análogo discreto de teorema de Taylor . Está estrechamente relacionado con Polinomio de Newton. Alternando sumas de esta forma se pueden expresar como la Nørlund-Arroz integral.
En particular, se puede expresar el producto de los coeficientes binomiales como una combinación lineal de este tipo:
donde los coeficientes de conexión son coeficientes multinomiales. En términos de objetos etiquetados combinatorias, los coeficientes de conexión representan el número de formas de asignar M + nk etiquetas a un par de objetos combinatorios marcados de peso m y n respectivamente, que han tenido sus etiquetas primero k identificados, o pegadas entre sí, con el fin para obtener un nuevo objeto combinatoria etiquetado de peso m + nk. (Es decir, para separar las etiquetas en 3 porciones que se aplicarán a la parte pegada, la parte sin pegar del primer objeto, y la parte despegado del segundo objeto.) En este sentido, los coeficientes binomiales son a exponencial generando serie lo la caída de los factoriales son series de generación ordinaria.
Serie binomial de Newton
Newton serie binomial, el nombre de Sir Isaac Newton , es uno de los más sencillos Serie Newton:
La identidad puede obtenerse mostrando que ambos lados satisfacen la ecuación diferencial (1+ z) f '(z) = α f (z).
La radio de convergencia de esta serie es 1. Una expresión alternativa es
donde la identidad
está aplicado.
La fórmula para la serie binomial fue grabada en la lápida de Newton en la Abadía de Westminster en 1727.
Generalización de q -Serie
El coeficiente binomial tiene una generalización q-analógico conocido como el Binomial gaussiana.
Generalización a cardenales infinitos
La definición del coeficiente binomial se puede generalizar a cardenales infinitos definiendo:
donde A es un conjunto con cardinalidad  . Se puede demostrar que el coeficiente binomial generalizado está bien definido, en el sentido de que no importa lo que establece elegimos para representar el número cardinal
. Se puede demostrar que el coeficiente binomial generalizado está bien definido, en el sentido de que no importa lo que establece elegimos para representar el número cardinal  ,
, 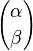 seguirá siendo el mismo. Para cardenales finitos, esta definición coincide con la definición estándar del coeficiente binomial.
seguirá siendo el mismo. Para cardenales finitos, esta definición coincide con la definición estándar del coeficiente binomial.
Suponiendo que la Axioma de elección, uno puede demostrar que 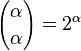 para cualquier cardinal infinito
para cualquier cardinal infinito  .
.
Coeficiente binomial en lenguajes de programación
La notación  es conveniente en la escritura a mano, pero un inconveniente para máquinas de escribir y terminales de ordenador. Muchos lenguajes de programación no ofrecen un estándar subrutina para calcular el coeficiente binomial, pero por ejemplo la Lenguaje de programación J utiliza el signo de exclamación: k! n.
es conveniente en la escritura a mano, pero un inconveniente para máquinas de escribir y terminales de ordenador. Muchos lenguajes de programación no ofrecen un estándar subrutina para calcular el coeficiente binomial, pero por ejemplo la Lenguaje de programación J utiliza el signo de exclamación: k! n.
Implementaciones ingenuos, como el siguiente fragmento en C :
int elegir (int n, int k) {
volver factorial (n) / (factorial (k) * factorial (n - k));
}
son propensos a desbordarse errores, lo que restringe gravemente la gama de valores de entrada. Una aplicación directa de la primera definición funciona bien:
unsigned long long elegir (n sin firmar, sin firmar k) {
si (k> n)
return 0;
si (k> n / 2)
k = nk; // Más rápido
largo doble acum = 1;
for (i = 0 sin firmar; i ++ <k;)
acum = acum * (n-k + i) / i;
retorno acum + 0,5; // Evitar el error de redondeo
}
Uso Regla de Pascal 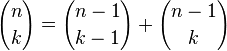 , El algoritmo para el coeficiente binomial puede escribirse en forma recursiva:
, El algoritmo para el coeficiente binomial puede escribirse en forma recursiva:
función de elegir (n: número entero, k: entero): número entero
si k = 0 o k = n entonces
elegir = 1
más
elegir elegir = (n-1, k-1) + elegir (n-1, k)
terminara si
función final
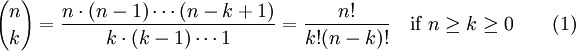
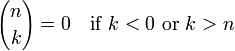
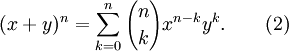


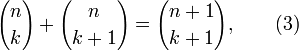


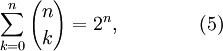

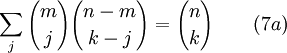
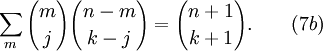
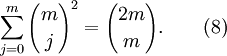
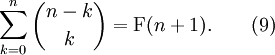




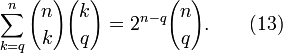

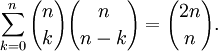


![\ Sum_ {k = 0} ^ {n} {n \ choose k} = n! [Z ^ n] \ exp (2z) = 2 ^ n,](../../images/197/19718.png)

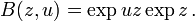
![{N \ choose k} = n! [U ^ k] [z ^ n] \ exp uz \ exp z = n! [Z ^ n] \ frac {z ^ k} {k!} \ Exp z](../../images/197/19722.png)
![\ Frac {n!} {K!} [Z ^ {n-k}] \ exp z = \ frac {n!} {K! \, (N-k)!},](../../images/197/19723.png)