
OEIS
Antecedentes
Esta selección se hace para las escuelas por caridad para niños leer más . Haga clic aquí para obtener más información sobre SOS Children.
La Enciclopedia On-Line de secuencias del número entero (OEIS), también citó simplemente como Sloane, es una extensa búsqueda base de datos de secuencias de números enteros, de libre disposición en la Web .
OEIS registra información sobre secuencias enteras de interés para ambos profesionales matemáticos y aficionados, y es ampliamente citado. Contiene más de 135.000 secuencias, lo que es la mayor base de datos de su clase.
Cada entrada contiene los principales términos de la sucesión, palabras clave, motivaciones matemáticos, enlaces de literatura, y más, incluyendo la opción de generar un gráfico o un juego representación musical de la secuencia. La base de datos es buscar por palabra clave y por subsecuencia.
Historia
Neil Sloane empezó a recoger las secuencias de números enteros como estudiante a mediados de 1960 de apoyar su trabajo en la combinatoria . La base de datos se almacena en un primer momento en tarjetas perforadas. Publicó selecciones de la base de datos en forma de libro en dos ocasiones:
- Un Manual de secuencias del número entero (1973, ISBN 0-12-648550-X), que contiene 2400 secuencias.
- La Enciclopedia de secuencias del número entero con Simon Plouffe (1995, ISBN 0-12-558630-2), que contiene 5487 secuencias.
Estos libros fueron bien recibidos y, sobre todo después de la segunda publicación, los matemáticos suministran Sloane con un flujo constante de nuevas secuencias. La colección se volvió incontrolable en forma de libro, y cuando la base de datos había alcanzado 16.000 entradas Sloane decidió ir en línea por primera vez como un servicio de correo electrónico (agosto de 1994), y poco después como un sitio web (1995). La base de datos sigue creciendo a un ritmo de unas 10.000 entradas de un año.
Sloane ha gestionado personalmente "sus" secuencias desde hace casi 40 años, pero a partir de 2002, una junta de editores asociados y voluntarios ha ayudado a mantener la base de datos.
Como spin-off de la labor de base de datos, Sloane fundó la Diario de secuencias del número entero en 1998.
En 2004, Sloane celebró la adición de la secuencia número 100.000 de la base de datos, ![]() A100000. En 2006, la interfaz de usuario fue revisado y se añadieron capacidades de búsqueda más avanzados.
A100000. En 2006, la interfaz de usuario fue revisado y se añadieron capacidades de búsqueda más avanzados.
No enteros
Además de las secuencias de números enteros en sentido estricto, OEIS también catalogó secuencias de fracciones , los dígitos del números trascendentes, números complejos y así sucesivamente por transformarlos en secuencias de números enteros.
Las secuencias de números racionales están representados por dos secuencias (nombrados con la palabra clave 'frac'): la secuencia de los numeradores y la secuencia de los denominadores. Por ejemplo, el quinto orden Secuencia de Farey,  , Está catalogado como el numerador secuencia de 1, 1, 1, 2, 1, 3, 2, 3, 4 (
, Está catalogado como el numerador secuencia de 1, 1, 1, 2, 1, 3, 2, 3, 4 ( ![]() A006842) y el denominador secuencia de 5, 4, 3, 5, 2, 5, 3, 4, 5 (
A006842) y el denominador secuencia de 5, 4, 3, 5, 2, 5, 3, 4, 5 ( ![]() A006843).
A006843).
Números irracionales importantes como π = 3.1415926535897 ... se catalogan bajo secuencias enteras representativos como expansiones decimales (en este caso 3, 1, 4, 1, 5, 9, 2, 6, ... ( ![]() A000796)) o desarrollo en fracciones continuas (aquí 3, 7, 15, 1, 292, 1, ... (
A000796)) o desarrollo en fracciones continuas (aquí 3, 7, 15, 1, 292, 1, ... ( ![]() A001203)).
A001203)).
Convenciones
El OEIS se limita actualmente a llano ASCII de texto, por lo que utiliza una forma lineal de la notación matemática convencional (como f (n) para las funciones, n para las variables de funcionamiento, etc.). letras griegas suelen estar representados por sus nombres completos, por ejemplo, , MU para μ, PHI para φ.
Cada secuencia se identifica por la letra A seguida de seis dígitos, denominado a veces sin los ceros iniciales, por ejemplo, A315 en lugar de A000315.
Términos individuales de secuencias están separadas por comas. Grupos de dígitos no están separados por comas, puntos o espacios.
En los comentarios, fórmulas, etc., a (n) representa el enésimo término de la sucesión.
Significado especial de cero
Zero se utiliza a menudo para representar la secuencia de elementos inexistentes. Por ejemplo, ![]() A104157 enumera el "primo más pequeño de n ² consecutivos prepara para formar un n × n cuadrado mágico de menos constante mágica, o 0 si no existe tal cuadrado mágico. " El valor de un (1) (un cuadrado de 1 x 1 magia) es 2; a (3) es 1480028129. Pero no hay tal cuadrado de 2 × 2 magia, por lo que una (2) es 0.
A104157 enumera el "primo más pequeño de n ² consecutivos prepara para formar un n × n cuadrado mágico de menos constante mágica, o 0 si no existe tal cuadrado mágico. " El valor de un (1) (un cuadrado de 1 x 1 magia) es 2; a (3) es 1480028129. Pero no hay tal cuadrado de 2 × 2 magia, por lo que una (2) es 0.
Este uso especial tiene una base matemática sólida en ciertas funciones de conteo. Por ejemplo, la función de valencia totient  (
( ![]() A014197) cuenta las soluciones de φ (x) = m. Hay 4 soluciones para 4, pero no hay soluciones para los 14, por lo tanto, una (14) de A014197 es 0-no hay soluciones.
A014197) cuenta las soluciones de φ (x) = m. Hay 4 soluciones para 4, pero no hay soluciones para los 14, por lo tanto, una (14) de A014197 es 0-no hay soluciones.
Ocasionalmente -1 se usa para este propósito en su lugar, como en ![]() A072041.
A072041.
Ordenación lexicográfica
El OEIS mantiene la orden lexicográfico de las secuencias, por lo que cada secuencia tiene un predecesor y un sucesor (su "contexto"). OEIS normaliza las secuencias de ordenación lexicográfica, (por lo general) haciendo caso omiso de ceros o unos iniciales y también el signo de cada elemento. Las secuencias de códigos de distribución de peso suelen omitir los ceros periódicamente recurrentes.
Por ejemplo, considere: los números primos , los primos palíndromos, la sucesión de Fibonacci , el secuencia del abastecedor perezoso, y los coeficientes de la expansión de la serie de 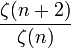 . En OEIS orden lexicográfico, que son:
. En OEIS orden lexicográfico, que son:
Secuencia # 1: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...
Secuencia # 2: 2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, ...
Secuencia # 3: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...
Secuencia 4: 1, 2, 4, 7, 11, 16, 22, 29, 37, 46, 56, 67, 79, 92, ...
Secuencia # 5: 1, -3, -8, -3, -24, 24, -48, -3, -8, 72, -120, 24, -168, 144, ...
mientras ordenamiento lexicográfico unnormalized ordenaría estas secuencias así: # 3, # 5, # 4, # 1, # 2.
Autorreferencialidad
Muy temprano en la historia de la OEIS, muchas personas sugirieron secuencias derivadas de la colocación de las secuencias en el propio OEIS. "Me resistí a la adición de estas secuencias por mucho tiempo, en parte por el deseo de mantener la dignidad de la base de datos, y en parte porque A22 sólo conocían a 11 términos!" Sloane recordó.
Una de las secuencias más temprana autorreferenciales Sloane aceptados en la OEIS era ![]() A031135 (más tarde
A031135 (más tarde ![]() A091967) "a (n) = n-ésimo término de la secuencia A_n." Esta secuencia estimuló el progreso en la búsqueda de más términos de
A091967) "a (n) = n-ésimo término de la secuencia A_n." Esta secuencia estimuló el progreso en la búsqueda de más términos de ![]() A000022. Para n mayor que corresponden a las secuencias que son finitos y teniendo en cuenta en su totalidad (palabras clave "fini" y "completo"), un término (n) de A091967 no está definido.
A000022. Para n mayor que corresponden a las secuencias que son finitos y teniendo en cuenta en su totalidad (palabras clave "fini" y "completo"), un término (n) de A091967 no está definido.
![]() A100544 lista el primer término dado en la secuencia A n, pero necesita ser actualizada de vez en cuando debido al cambio de opiniones sobre las compensaciones. Añadir lugar plazo de un (1) de la secuencia A n puede parecer una buena alternativa si no fuera por el hecho de que algunas secuencias tienen compensaciones de 2 y superiores.
A100544 lista el primer término dado en la secuencia A n, pero necesita ser actualizada de vez en cuando debido al cambio de opiniones sobre las compensaciones. Añadir lugar plazo de un (1) de la secuencia A n puede parecer una buena alternativa si no fuera por el hecho de que algunas secuencias tienen compensaciones de 2 y superiores.
Esta línea de pensamiento lleva a la pregunta "¿Es n en la secuencia A n?" y las secuencias deliciosamente paradójicos ![]() A053873, n es en A n, y
A053873, n es en A n, y ![]() A053169, n no es en A n. Así, el número compuesto 2808 está en A053873 porque
A053169, n no es en A n. Así, el número compuesto 2808 está en A053873 porque ![]() A002808 es la secuencia de números compuestos, mientras que los no-prime 40 está en A053169 porque no es en A000040, los números primos. La paradoja es que las secuencias Qué 53.169 y 53.873 pertenecen a? (Esta es una forma de La paradoja de Russell.)
A002808 es la secuencia de números compuestos, mientras que los no-prime 40 está en A053169 porque no es en A000040, los números primos. La paradoja es que las secuencias Qué 53.169 y 53.873 pertenecen a? (Esta es una forma de La paradoja de Russell.)
Un ejemplo simplificado de una entrada típica OEIS
Esta entrada, ![]() A046970, fue elegido porque, con la excepción de una Programa de arce, que contiene todos los campos de una entrada OEIS puede tener.
A046970, fue elegido porque, con la excepción de una Programa de arce, que contiene todos los campos de una entrada OEIS puede tener.
Número de Identificación: A046970 URL: http://www.research.att.com/projects/OEIS?Anum=A046970 Secuencia: 1,3,8,3,24,24,48,3,8,72,120,24,168,144,192,3,288 , 24,360,72, 384,360,528,24,24,504,8,144,840,576,960,3,960,864,1152,24, 1368,1080,1344,72,1680,1152,1848,360,192,1584,2208,24,48,72, 2304,504,2808 , 24,2880,144,2880,2520,3480,576 Firmado: 1, -3, -8, -3, -24,24, -48, -3, -8,72, -120,24, -168144192 , -3, -288, 24, -360,72,384,360, -528,24, -24504, -8144, -840, -576, -960, -3, 960,864,1152,24, -1368,1080,1344, 72, -1680, -1152, -1848.360, 192,1584, -2208,24, -48,72,2304,504, -2808,24,2880,144,2880, 2520, -3480, -576 Nombre : Creado a partir de la función zeta de Riemann: coeficientes de expansión de la serie de Zeta (n + 2) / Zeta (n). Comentarios: ... Aparte de signos también sum_ {d | n} núcleo (d) ^ 2 * mu (n / d) en su núcleo (x) es la parte squarefree de x. - Benoit Cloitre (abcloitre (AT) modulonet.fr), 31 de mayo 2002 Referencias M. Abramowitz y IA Stegun, Handbook of Mathematical Functions, Dover Publications, 1965, pp 805-811.. Enlaces: función zeta Wikipedia, Riemann. Fórmula: multiplicativa con un (p ^ e) = 1-p ^ 2. a (n) = sum_ {d | n} mu (d) * d ^ 2. Ejemplo: una (3) = -8 porque los divisores de 3 son {1, 3}, y mu (1) * 1 ^ 2 + mu (3) * 3 ^ 2 = -8. a (4) = -3 porque los divisores de 4 son {1, 2, 4}, y mu (1) * 1 ^ 2 + mu (2) * 2 ^ 2 + mu (4) * 4 ^ 2 = - 3 Math'ca: Mudd [d_]: = MoebiusMu [d] * d ^ 2; Tabla [Plus@@Mudd [Divisores [n]], {n, 60}] (López) Programa: (PARI) A046970 (n) = sumdiv (n, d, d ^ 2 * moebius (d)) (Benoit Cloitre ) Ver también: Secuencia en contexto: A016623 A046543 A035292 this_sequence A058936 A002017 A086179 secuencias adyacentes: A046967 A046968 A046969 this_sequence A046971 A046972 A046973 Cfr A027641 y A027642. Palabras clave: signo, mult Offset: 1 Autor (s): Douglas Stoll, dougstoll (AT) email.msn.com Extensión: Se ha corregido y ampliado por Vladeta Jovovic (Vladeta (AT) Eunet.yu), 25 de julio 2001 ... Los campos de entrada
Número de identificación
Cada secuencia en el OEIS tiene una número de serie, un número entero positivo de seis dígitos, con el prefijo A (y con relleno de ceros a la izquierda, antes de noviembre de 2004). La letra "A" significa "absoluta". Los números están bien asignadas por el editor (s) o por un Distribuidor número, que es muy útil para cuando los contribuyentes desean enviar en secuencias relacionadas a la vez y ser capaz de crear referencias cruzadas. Un número A del dispensador expira un mes a partir de tema si no se utiliza. Pero a medida que la siguiente tabla de secuencias seleccionadas arbitrariamente mostrar, la correspondencia aproximada sostiene.
| A059097 | N números tales que el coeficiente binomial C (2n, n) no es divisible por el cuadrado de un primo impar. | 01 de enero 2001 |
| A060001 | Fibonacci (n) !. | 14 de marzo 2001 |
| A066288 | Número de poliominós 3 dimensiones (o policubos) con n celdas y grupo de simetría de orden exactamente 24. | 01 de enero 2002 |
| A075000 | Número más pequeño de tal manera que n * a (n) es una concatenación de n enteros consecutivos ... | 31 de agosto 2002 |
| A078470 | Fracción continua de Zeta (3/2) | 01 de enero 2003 |
| A080000 | Número de permutaciones que cumplan -k <= p (i) -i <= r y p (i) -i | 10 de febrero 2003 |
| A090000 | Longitud de los más largos bloque contiguo de 1 de la expansión binaria de n-ésimo primo. | 20 de noviembre 2003 |
| A091345 | Convolución exponencial de A069321 (n) con la misma, donde nos pusimos A069321 (0) = 0. | 01 de enero 2004 |
| A100000 | Marcas del 22.000 años hueso Ishango del Congo. | 07 de noviembre 2004 |
| A102231 | Columna 1 de triángulo A102230, y es igual a la convolución de A032349 A032349 con desplazamiento a la derecha. | 01 de enero 2005 |
| A110030 | Número de enteros consecutivos comenzando con n necesaria para sumar a un número Niven. | 08 de julio 2005 |
| A112886 | Sin triángulos enteros positivos. | 12 de enero 2006 |
| A120007 | Mobius transformada de suma de factores primos de n | 02 de junio 2006 |
Incluso para las secuencias en los predecesores libro a la OEIS, los números de identificación no son los mismos. El 1973 Manual de secuencias del número entero contenía alrededor de 2.400 secuencias, que fueron numerados por orden lexicográfico (la letra M más 4 dígitos, acolchados cero en caso necesario), y la Enciclopedia de secuencias del número entero de 1995 contenía 5.487 secuencias, también numeradas por orden lexicográfico (el letra N más 4 dígitos, acolchados cero en caso necesario). Estos viejos números M y N, en su caso, se encuentran en el campo de número de identificación entre paréntesis después del moderno Un número.
URL
El campo URL da el formato preferido para la dirección URL para enlazar a la secuencia en cuestión, para simplificar cortar y pegar.
Secuencia
El campo de secuencia muestra los mismos, o por valor de al menos aproximadamente cuatro líneas 'números. El campo de secuencia no hace distinción entre las secuencias que son finitos, pero todavía demasiado tiempo para mostrar y secuencias que son infinitas. Para ayudar a hacer esa determinación, que hay que buscar en el campo de palabras clave para "fini", "completo" o "más". Para determinar a qué n los valores dados corresponden, ver el campo de desplazamiento, lo que da la n para el primer término dado.
Cualquier signo negativo se eliminan de este campo, y los valores con signos se ponen en el campo Firmado.
Firmado
El campo firmado es casi lo mismo que el campo de secuencia excepto que muestra signos negativos. Este campo sólo se incluye para secuencias que tienen valores negativos. Cualquier entrada a este campo debe tener la palabra clave "señal".
Nombre
El campo de nombre por lo general contiene el nombre más común para la secuencia, ya veces también la fórmula. Por ejemplo, 1, 8, 27, 64, 125, 216, 343, 512, ( ![]() A000578) se llama "Los cubos: a (n) = n ^ 3."
A000578) se llama "Los cubos: a (n) = n ^ 3."
Comentarios
El campo de comentarios es para obtener información sobre la secuencia que no encaja del todo en cualquiera de los otros campos. El campo de comentarios a menudo señala relaciones interesantes entre las diferentes secuencias y aplicaciones menos obvias para una secuencia. Por ejemplo, Lekraj Beedassy en un comentario a A000578 señala que los números de cubo también cuentan el "número total de triángulos resultantes de entrecruzamiento cevians dentro de un triángulo, de modo que dos de sus lados son cada uno n-particionada ", mientras Sloane señala la relación inesperada entre los números hexagonales centradas ( ![]() A003215) y segundo polinomios de Bessel (
A003215) y segundo polinomios de Bessel ( ![]() A001498) en un comentario a A003215.
A001498) en un comentario a A003215.
Si no se da el nombre de un comentario, el comentario fue hecho por el remitente original de la secuencia.
Arce, Mathematica, y otros programas
Arce y Mathematica son los programas preferidos para el cálculo de las secuencias en la OEIS, y ambos obtienen sus propias etiquetas de campo, "Maple" y "Mathematica". Cualquier otro programa para crear una etiqueta de campo genérico "Programa" y el nombre del programa en paréntesis. El OEIS tiene programas en PARI, Magma, Matlab, Python e incluso Microsoft Excel.
Si no hay un nombre dado, el programa fue escrito por el remitente original de la secuencia.
Palabras clave
El OEIS tiene su propio conjunto estándar de cuatro o cinco palabras clave de letras que caracterizan a cada secuencia:
- base de los resultados del cálculo dependen de una base posicional específico. Por ejemplo, 2, 3, 5, 7, 11, 101, 131, 151, 181 ...
 A002385 son números primos, independientemente de la base, pero son palindrómica específicamente en base 10. La mayoría de ellos no son palindrómica en binario. Algunas secuencias califica a esta palabra clave en función de cómo se definen. Por ejemplo, 3, 7, 31, 127, 8191, 131071, ...
A002385 son números primos, independientemente de la base, pero son palindrómica específicamente en base 10. La mayoría de ellos no son palindrómica en binario. Algunas secuencias califica a esta palabra clave en función de cómo se definen. Por ejemplo, 3, 7, 31, 127, 8191, 131071, ...  A000668 no tiene precio "base" si se ha definido como "primos de la forma 2 ^ n - 1." Sin embargo, que se define como "primos Repunit en binario", la secuencia sería puntúa la palabra clave "base".
A000668 no tiene precio "base" si se ha definido como "primos de la forma 2 ^ n - 1." Sin embargo, que se define como "primos Repunit en binario", la secuencia sería puntúa la palabra clave "base". - bref "secuencia es demasiado corta como para hacer cualquier análisis con", por ejemplo,
 A079243, Número de clases de isomorfismo de operaciones no conmutativa asociativas no anti-asociativas anti-conmutativos binarios cerrados en un conjunto de orden n.
A079243, Número de clases de isomorfismo de operaciones no conmutativa asociativas no anti-asociativas anti-conmutativos binarios cerrados en un conjunto de orden n. - cofr La secuencia representa una fracción continua.
- contras La secuencia es una expansión decimal de un importante matemático constante, como el correo o π.
- Un núcleo secuencia que es de importancia fundamental para una rama de las matemáticas, como los números primos, la sucesión de Fibonacci, etc.
- muertos Esta palabra clave se utiliza para secuencias erróneas que han aparecido en los periódicos o libros, o de duplicados de secuencias existentes. Por ejemplo,
 A088552 es el mismo que A000668.
A088552 es el mismo que A000668. - mudo Una de las palabras más subjetivas, por "secuencias sin importancia", que pueden o no estar relacionados directamente con las matemáticas.
 A001355, "Mix dígitos de pi y e." es un ejemplo de la primera, y
A001355, "Mix dígitos de pi y e." es un ejemplo de la primera, y  A082390, "Los números en un teclado de computadora, leer en una espiral." es un ejemplo de este último.
A082390, "Los números en un teclado de computadora, leer en una espiral." es un ejemplo de este último. - fácil Los términos de la secuencia se puede calcular fácilmente. Tal vez la secuencia más merecedores de esta palabra clave es 1, 2, 3, 4, 5, 6, 7, ...
 A000027, donde cada término es 1 más que el término anterior. La palabra clave "fácil" a veces se le da a las secuencias "primos de la forma f (m)", donde f (m) es una función fácil de calcular. (Aunque incluso si f (m) es fácil de calcular por gran m, puede ser muy difícil determinar si f (m) es primo).
A000027, donde cada término es 1 más que el término anterior. La palabra clave "fácil" a veces se le da a las secuencias "primos de la forma f (m)", donde f (m) es una función fácil de calcular. (Aunque incluso si f (m) es fácil de calcular por gran m, puede ser muy difícil determinar si f (m) es primo). - eigen Una secuencia de valores propios .
- fini La secuencia es finito, aunque aún podría contener más términos que pueden mostrarse. Por ejemplo, el campo de secuencia de
 A105417 muestra sólo una cuarta parte de todos los términos, pero un comentario señala que el último término es de 3888.
A105417 muestra sólo una cuarta parte de todos los términos, pero un comentario señala que el último término es de 3888. - frac Una secuencia de cualquiera de numeradores o denominadores de una secuencia de fracciones que representan números racionales. Cualquier secuencia con esta palabra clave debe, hará referencia a su secuencia coincidente de numeradores o denominadores, aunque esto se puede prescindir de las secuencias de Fracciones egipcias, tales como
 A069257, donde la secuencia de numeradores sería
A069257, donde la secuencia de numeradores sería  A000012. Esta palabra clave no debe utilizarse para las secuencias de las fracciones continuas, cofr debe utilizarse en lugar para ese propósito.
A000012. Esta palabra clave no debe utilizarse para las secuencias de las fracciones continuas, cofr debe utilizarse en lugar para ese propósito. - El pleno campo de secuencia muestra la secuencia completa. Si una secuencia tiene la palabra clave "completo", sino que también debe tener el "fini." Palabra clave Un ejemplo de una secuencia finita dada en su totalidad es el de la primos supersingular
 A002267, de los cuales no son precisamente quince.
A002267, de los cuales no son precisamente quince. - duro Los términos de la secuencia no se pueden calcular fácilmente, incluso con número prima crujido poder. Esta palabra clave se utiliza con mayor frecuencia para las secuencias correspondientes a problemas no resueltos, tales como "¿Cuántas esferas pueden tocar a otra esfera del mismo tamaño?"
 A001116 enumera las diez primeras soluciones conocidas.
A001116 enumera las diez primeras soluciones conocidas. - menos una "secuencia de menos interesante".
- más Los próximos términos de la sucesión no se conocen.
- información The secuencia corresponde a una función multiplicadora. Plazo de un (1) debe ser de 1, y un término (mn) puede ser calculado multiplicando a (m) de un (n) si m y n son primos entre sí. Por ejemplo, en
 A046970, a (12) = a (3) a (4) = -8 × -3.
A046970, a (12) = a (3) a (4) = -8 × -3. - nuevo Para las secuencias que fueron añadidos en el último par de semanas, o tenían una importante ampliación recientemente. Esta palabra clave no se le da una casilla en el formulario web para la presentación de nuevas secuencias, el programa de Sloane lo añade de forma predeterminada en su caso.
- agradable Tal vez la palabra clave más subjetivo de todos, porque "excepcionalmente agradable secuencias."
- nonn La secuencia consiste en números enteros no negativos (que puede incluir ceros). No se hace distinción entre las secuencias que consisten en números no negativos sólo por los elegidos de compensación (por ejemplo, n 3, los cubos, que son todos positivos de n = 0 forwards) y los que por definición son totalmente no negativa (por ejemplo, n 2, las plazas).
- obsc La secuencia se considera oscura y necesita una mejor definición. Una secuencia con esta palabra clave,
 A025046 se ha mirado por al menos otro colaborador OEIS que era incapaz de reproducir los resultados dados por el solicitante original.
A025046 se ha mirado por al menos otro colaborador OEIS que era incapaz de reproducir los resultados dados por el solicitante original. - libertad condicional secuencias que "puede ser borrado más tarde a discreción del editor."
- firmar algunos (o todos) de los valores de la secuencia son negativos. La entrada incluye un campo Firmado con los signos y un campo de secuencia que consta de todos los valores pasados a través del valor absoluto función.
- tabf "Una matriz irregular (o de forma divertida) de números realizados en una secuencia de lectura fila por fila." Por ejemplo,
 A071031, "Triángulo leído por filas dando sucesivos estados de autómata celular generada por" regla de 62. "
A071031, "Triángulo leído por filas dando sucesivos estados de autómata celular generada por" regla de 62. " - Tabl Una secuencia obtenida mediante la lectura de una disposición geométrica de números, como un triángulo o cuadrado, fila por fila. El ejemplo por excelencia es el triángulo de Pascal leído por filas,
 A007318.
A007318. - UNED Sloane no ha editado la secuencia, pero cree que podría ser vale la pena incluir en la OEIS. La secuencia podría contener errores de cálculo o tipográfico. Se invita a los contribuyentes a reflexionar sobre la secuencia y enviar Sloane su edición.
- Desc "Poco se sabe" acerca de la secuencia, ni siquiera la fórmula que lo produce. Por ejemplo,
 A072036, que se presentó a un oráculo de Internet para reflexionar.
A072036, que se presentó a un oráculo de Internet para reflexionar. - a pie "paseos Condes (o caminos autónomos evitar)."
- palabra Depende de las palabras de un idioma específico. Por ejemplo, cero, uno, dos, tres, cuatro, cinco, etc., 4, 3, 3, 5, 4, 4, 3, 5, 5, 4, 3, 6, 6, 8, 8, 7, 7, 9, 8, 8 ...
 A005589, "Número de letras en el nombre Inglés de n, con exclusión de los espacios y guiones."
A005589, "Número de letras en el nombre Inglés de n, con exclusión de los espacios y guiones."
Algunas palabras clave son excluyentes entre sí, a saber: núcleo y mudo, fácil y duro, lleno y más, menos y agradable, y nonn y firmar.
Offset
El desplazamiento es el índice del primer término dado. Para algunas secuencias, el desplazamiento es obvio. Por ejemplo, si enumeramos la secuencia de números cuadrados como 0, 1, 4, 9, 16, 25 ..., el desplazamiento es 0; mientras que si lo listamos como 1, 4, 9, 16, 25 ..., el desplazamiento es 1. El desplazamiento predeterminado es 0, y la mayoría de las secuencias en la OEIS haber compensado de 0 ó 1. Secuencia ![]() A073502, la constante mágica de n × n cuadrado mágico con las entradas de la carrera (en relación con al menos 1 primo) con pequeñas sumas de filas, es un ejemplo de una secuencia con desplazamiento de 3, y
A073502, la constante mágica de n × n cuadrado mágico con las entradas de la carrera (en relación con al menos 1 primo) con pequeñas sumas de filas, es un ejemplo de una secuencia con desplazamiento de 3, y ![]() A072171, "Número de estrellas de magnitud visual n." es un ejemplo de una secuencia con desplazamiento de -1.
A072171, "Número de estrellas de magnitud visual n." es un ejemplo de una secuencia con desplazamiento de -1.
A veces puede haber desacuerdo sobre cuáles son los términos iniciales de la secuencia son, y en consecuencia lo que la compensación debe ser. En el caso de la secuencia del abastecedor perezoso, el número máximo de piezas se puede cortar una torta en con n cortes, la OEIS da la secuencia como 1, 2, 4, 7, 11, 16, 22, 29, 37, ... ![]() A000124, con el desplazamiento 0, mientras que Mathworld da la secuencia como 2, 4, 7, 11, 16, 22, 29, 37, ... (implícita compensado 1). Se puede argumentar que sin hacer cortes a la tortita es técnicamente una serie de recortes, es decir, n = 0. Pero puede también argumentar que un panqueque sin cortar es irrelevante para el problema.
A000124, con el desplazamiento 0, mientras que Mathworld da la secuencia como 2, 4, 7, 11, 16, 22, 29, 37, ... (implícita compensado 1). Se puede argumentar que sin hacer cortes a la tortita es técnicamente una serie de recortes, es decir, n = 0. Pero puede también argumentar que un panqueque sin cortar es irrelevante para el problema.
Aunque el desplazamiento es un campo necesario, algunos contribuyentes no se molestan en comprobar si el desplazamiento de 0 por defecto es apropiado para la secuencia en que están enviando.
El formato interno en realidad muestra dos números para el desplazamiento. El primero es el número descrito anteriormente, mientras que el segundo representa el índice de la primera entrada (contando desde 1) que tiene un valor absoluto mayor que 1. Este segundo valor se utiliza para acelerar el proceso de búsqueda de una secuencia. Así ![]() A000001, que comienza 1, 1, 1, 2 con la primera entrada que representa una (1) tiene 1, 4 como el valor interno de la campo de desplazamiento.
A000001, que comienza 1, 1, 1, 2 con la primera entrada que representa una (1) tiene 1, 4 como el valor interno de la campo de desplazamiento.
Autor (s)
El autor de la secuencia es la persona que presentó la secuencia, incluso si la secuencia ha sido conocido desde la antigüedad. El nombre del remitente se le da nombre (escrito con todas las letras), inicial (s) (si procede) y apellido; esto en contraste con la forma en que los nombres están escritos en los campos de referencia. También se da la dirección de correo del remitente, con el carácter @ sustituida por "(AT)". Para la mayoría de las secuencias después A055000, el campo autor también incluye la fecha en que el remitente envió en la secuencia. Pero cuando el remitente es uno de los contribuyentes más frecuentes el campo de autor sólo tiene las iniciales; "njas" para el propio Neil Sloane, por ejemplo.
Buscando en la OEIS
La versión anterior de la página principal de consulta de la OEIS ofrecido tres maneras de ver hasta secuencias, y el botón de la derecha tuvo que ser seleccionado. Hubo una página avanzada de búsqueda, pero su utilidad se ha integrado en la página principal de búsqueda en un importante rediseño de la interfaz en enero de 2006.
Introduzca una secuencia
Introduzca unas pocas términos de la sucesión, separadas por espacios o comas (o ambos).
Puede introducir signos negativos, pero serán ignoradas. Por ejemplo, 0, 3, 7, 13, 20, 28, 36, 43, 47, 45, 32, 0, -64, n 2 menos el n-ésimo número de Fibonacci, es una secuencia que técnicamente no está en la OEIS, pero el muy similar secuencia 0, -3, -7, -13, -20, -28, -36, -43, -47, -45, -32, 0, 64, se encuentra en la OEIS y le aparecerá cuando uno busca su homólogo signos invertido.
Sin embargo, la búsqueda puede ser obligado a coincidir con los signos mediante el uso de la "señal:" prefijo en la cadena de búsqueda. Esto es especialmente útil para las secuencias como ![]() A008836 que consiste exclusivamente en los positivos y negativos.
A008836 que consiste exclusivamente en los positivos y negativos.
Uno puede entrar en tan poco como un único entero o hasta cuatro líneas de términos. Sloane recomienda entrar seis términos, a (2) a una (7), con el fin de obtener suficientes resultados, pero no demasiados resultados. Hay casos en los que entra un solo número entero da precisamente uno de los resultados, tal como 1990661 trae justo ![]() A007597, la primos strobogrammatic). Y también hay casos en los que uno puede entrar en muchos términos y todavía no restringir los resultados tanto.
A007597, la primos strobogrammatic). Y también hay casos en los que uno puede entrar en muchos términos y todavía no restringir los resultados tanto.
Introduzca una palabra
Introduzca una cadena de caracteres alfanuméricos. Algunos caracteres, como letras extranjeras acentuados, no están permitidos. Por lo tanto, para buscar secuencias relacionadas con Problema de Znám, intente entrar en él sin los acentos: "El problema de Znam." El manejo de los apóstrofes se ha mejorado mucho en el rediseño de 2006. Las cadenas de búsqueda " triángulo de Pascal , "" Pascals triángulo "y" triángulo de Pascal "todos dan los resultados deseados.
Para buscar más números poligonales por palabra, intentan "números n-gonal" en lugar de "números de prefijo gonal griegos" (por ejemplo, "los números 47-gonales" en lugar de "números heptaquartagonal"). Más allá de " números dodecagonales ", palabra que buscan con los prefijos griegos podrían dejar de producir los resultados deseados.
Introduzca un número de secuencia
Introduzca la OEIS moderna Un número de la secuencia, con la letra A y con o sin cero de relleno. A partir de 2006, los antiguos números de secuencia M y N producirán el resultado correcto como cadenas de búsqueda, por ejemplo, una búsqueda de M0422 traerá correctamente ![]() A006047, el número de entradas en n º fila del triángulo de Pascal no es divisible por 3 (M0422 en el libro La enciclopedia de secuencias del número entero) y no
A006047, el número de entradas en n º fila del triángulo de Pascal no es divisible por 3 (M0422 en el libro La enciclopedia de secuencias del número entero) y no ![]() A000422, la concatenación de los números de n hasta 1.
A000422, la concatenación de los números de n hasta 1.
Buscando desde un navegador Web
Una OpenSearch compatible navegador web (por ejemplo, Firefox 2.0 o Internet Explorer 7) puede tener OEIS añadido a su lista de búsqueda de la barra de herramientas basada añadiendo un proveedor con la siguiente URL: http://www.research.att.com/~njas/sequences/?q=TEST&language=english Entonces se puede introducir directamente la secuencia, por ejemplo, "1,2,6,24,120" (sin comillas) en la barra de búsqueda y buscar OEIS fácilmente.
