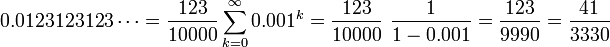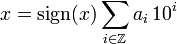Decimal
Acerca de este escuelas selección Wikipedia
Esta selección Escuelas fue originalmente elegido por SOS para las escuelas en el mundo en desarrollo que no tienen acceso a Internet. Está disponible como una descarga intranet. SOS Children ha cuidado de niños en África durante cuarenta años. ¿Puedes ayudar a su trabajo en África ?
| Sistemas de numeración por la cultura |
|---|
|
| Sistemas posicionales por base |
| Decimal (10) |
| Ternario Balanced |
| Lista de sistemas de numeración |
El decimal (base diez u ocasionalmente denario) sistema de numeración tiene diez como su base. Es el sistema de numeración más utilizado, tal vez porque los seres humanos tienen cuatro dedos y un pulgar en cada mano, dando un total de diez dígitos sobre ambas manos.
Notación decimal
Notación decimal es la escritura de los números en la base diez sistema de numeración , que utiliza varios símbolos (llamados dígitos ) por no más de diez valores distintos (0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 ) para representar los números, no importa lo grande. Estos dígitos se utilizan a menudo con una separador decimal que indica el comienzo de una parte fraccionaria, y con uno de los símbolos de signo + (positivo) o - (negativos) delante de los números para indicar señal. Sólo hay dos sistemas decimales verdaderamente posicionales en la civilización antigua, la Sistema de barras de conteo de China y el sistema numérico-hindú árabe, tanto requieren no más de diez símbolos. Otros sistemas numéricos requerir más o menos símbolos.
La sistema decimal es un sistema de numeración posicional; que tiene posiciones de las unidades, decenas, centenas, etc. La posición de cada dígito transmite el multiplicador (una potencia de diez) para ser utilizado con ese dígito-cada posición tiene un valor diez veces mayor que la de la posición a su derecha.
Diez es el número que es el conteo de los dedos y los pulgares de ambas manos (o dedos en los pies). En muchos idiomas la palabra dígitos o su traducción es también el término anatómico refiriéndose a los dedos de manos y pies. En Inglés, decimal (decimus < Lat. ) significa décima, diezmar medios reducen en una décima, y denario (denario <Lat.) significa que el unidad de diez. Los símbolos para los dígitos de uso común en torno a la mundo de hoy se llama Números arábigos por los europeos y Números indios por los árabes, los términos de los dos grupos, tanto en referencia a la cultura de la que aprendieron el sistema. Sin embargo, los símbolos utilizados en las diferentes áreas no son idénticos; por ejemplo, los números arábigos occidentales (de la que se derivan los números europeos) se diferencian de las formas utilizadas por otras culturas árabes.
Notaciones alternativas
Algunas culturas, o se utilizan para, utilizar otros sistemas de numeración, incluyendo precolombina Culturas mesoamericanas, como la Maya, que utilizan un sistema vigesimal (utilizando todos los dedos y veinte dedos de los pies), algunos nigerianos que utilizan varios duodecimal (base 12) sistemas, los babilonios , que utiliza sexagesimal (base 60), y el Yuki, quien habría usado octal (base 8).
Computer hardware y sistemas de software comúnmente utilizan una representación binaria , internamente. Para uso externo por especialistas en informática, esta representación binaria se presenta a veces en la relacionada octales o hexadecimales sistemas. Para la mayoría de propósitos, sin embargo, los valores binarios son convertidos a los valores decimales equivalentes para su presentación a y manipulación por los seres humanos.
Tanto el hardware y software también utilizan representaciones internas que se decimal eficaz para almacenar valores decimales y hacer aritmética. A menudo, esta aritmética se realiza sobre los datos que están codificados usando binario codificado decimal, pero hay otras representaciones decimales de uso (ver IEEE 754r), especialmente en implementaciones de bases de datos. Aritmética decimal se utiliza en ordenadores para que los resultados fraccionarios decimales pueden calcularse exactamente, lo que no es posible utilizando una representación fraccionaria binario. Esto es a menudo importante para los cálculos financieros y otros .
Las fracciones decimales
Una fracción decimal es una fracción donde el denominador es una potencia de diez.
Las fracciones decimales se expresan sin un denominador, la separador decimal que se inserta en el numerador (con ceros a la izquierda agregado si es necesario), en la posición de la derecha corresponde a la potencia de diez del denominador. por ejemplo, 08/10, 833/100, 83/1000, y 8/10000 se expresan como:. 0 8, 8 33, 0 083, 0 y 0008.... En los países de habla Inglés, un punto (·) o período se utiliza como separador decimal (.); en la mayoría de otros idiomas se utiliza una coma.
La parte entera o una parte integral de un número decimal es la parte a la izquierda del separador decimal (véase también la función del suelo). La parte del separador decimal a la derecha es la parte fraccionaria; si se considera como un número separado, un cero se escribe a menudo delante. Especialmente para los números negativos, tenemos que distinguir entre la parte fraccionaria de la notación y la parte fraccionaria del número en sí, ya que este último obtiene su propio signo menos. Es habitual para un número decimal que es menos de uno a tener un cero.
Ceros después de la coma decimal no son necesarios, aunque en la ciencia, la ingeniería y estadísticas que pueden ser retenidos para indicar una precisión requerida o para mostrar un nivel de confianza en la precisión de la serie:.. Mientras 0 080 0 y 08 son numéricamente igualdad de condiciones, en la ingeniería de 0. 080 sugiere una medición con un error de hasta 1 parte en dos mil (± 0. 0005), mientras que 0. 08 sugiere una medición con un error de hasta 1 en doscientos (ver Personajes importantes).
Otros números racionales
Cualquier número racional que no puede ser expresado como una fracción decimal tiene una expansión decimal infinito única terminando con decimales recurrentes.
Diez es el producto de la primera y la tercera números primos , uno mayor que el cuadrado del segundo número primo, y es uno menos que el quinto número primo. Esto lleva a un montón de fracciones decimales simples:
- Media = 0,5
- 1/3 = 0,333333 ... (con repetición de 3)
- 1/4 = 0,25
- 1/5 = 0,2
- 1/6 = 0,166666 ... (con 6 repitiendo)
- 1/8 = 0.125
- 1/9 = 0,111111 ... (con 1 repetición)
- 1/10 = 0,1
- 1/11 = 0,090909 ... (con 09 repitiendo)
- 1/12 = 0,083333 ... (con repetición de 3)
- 1/81 = 0.012345679012 ... (con 012.345.679 repetir)
Otros factores primos en el denominador darán más recurrentes secuencias , véase, por ejemplo 7, 13.
Que un número racional debe tener una expansión decimal finito o recurrente puede ser visto como una consecuencia de la división larga algoritmo , en que sólo hay q-1 posibilidad diferente de cero restos de la división por q, de modo que el patrón recurrente tendrán un período de menos de q. Por ejemplo para encontrar 03.07 por división larga:
0.4 2 8 5 7 1 4 ...
7) 3,0 0 0 0 0 0 0 0
2 8 30/7 = 4 r 2
2 0
1 4 20/7 = 2 r 6
6 0
5 6 8 r = 60/7 4
4 0
3 5 40/7 = 5 r 5
5 0
4 9 50/7 = 7 r 1
1 0
7 10/7 = 1 r 3
3 0
2 8 30/7 = 4 r 2 (de nuevo)
2 0
etc
Lo contrario a esta observación es que cada decimal periódico representa un número racional p / q. Esto es una consecuencia del hecho de la parte recurrente de una representación decimal es, de hecho, un infinito serie geométrica que se suma a un número racional. Por ejemplo,
Los números reales
Cada número real tiene una (posiblemente infinita) representación decimal, es decir, que se puede escribir como
donde
- signo () es el función de signo,
- un i ∈ {0,1, ..., 9} para todo i ∈ Z, son sus dígitos decimales, iguales a cero para todo i mayor que un número (que es el número de logaritmo común de | x |).
Dicha suma converge como i disminuye, incluso si hay un número infinito distinto de cero a i.
Los números racionales (por ejemplo, p / p) con factores primos en el denominador distinto de 2 y 5 (cuando se reduce a términos más simples) tienen un único representación decimal periódico.
Considere los números racionales que tienen sólo los factores 2 y 5 en el denominador, es decir, que se puede escribir como p / (2 a 5 b). En este caso no es una representación decimal de terminación. Por ejemplo 1/1 = 1, media = 0,5, 3/5 = 0,6, 3/25 = 0,12 y 1306/1250 = 1,0448. Tales números son los únicos números reales que no tienen una representación decimal único, ya que también pueden escribirse como una representación que tiene un recurrente 9, por ejemplo 1 = 0,99999 ..., media = 0,499999 ..., etc.
Esto deja a los números irracionales . También tienen representación decimal infinita única, y pueden ser caracterizados como los números cuya representación decimal ni resolución ni repetirse.
Así que, en general, la representación decimal es único, si se excluyen las representaciones que terminan en un recurrente 9.
Naturalmente, el mismo tricotomía es válido para otra base-n sistemas de numeración posicionales:
- Representación de terminación: donde el denominador racional divide algún n k
- Representación Recurrente: otro racional
- No termina, la representación no recurrente: irracional
y una versión de esto incluso es válido para los sistemas de numeración irracional-base, tal como representación de base media de oro.
Historia
A continuación una lista cronológica de los escritores decimales grabados.
Escritores decimales
- . c 3500 - 2500 aC Elamitas de Irán posiblemente utiliza formas tempranas de sistema decimal.
- . c 2900 aC egipcios jeroglíficos muestran contando en potencias de 10 (1.000.000 + 400.000 cabras, etc.) - ver Ifrah, por debajo
- . c 2600 aC la civilización del valle del Indo , el uso físico conocido más temprano de decimales fracciones en peso del sistema antiguo: 1/20, 1/10, 1/5, 1/2. Ver pesos y medidas antigua del valle del Indo
- . c 1400 aC chino escritores muestran familiaridad con el concepto: por ejemplo, 547 está escrito 'Quinientos más cuatro décadas, más de siete de días' en algunos manuscritos
- . c 1200 aC En la antigua India , el Texto védico Yajur-Veda establece los poderes de 10, hasta 10 55
- c. 400 aC Pingala - desarrolla el sistema de numeración binario para sánscrito prosodia, con una correspondencia clara con el sistema decimal en base 10
- c. 250 aC Arquímedes escribe el Contador de arena, que toma cálculo decimal hasta 10 80,000,000,000,000,000
- . c 100-200 La Satkhandagama escrito en la India - primer uso de logaritmos decimales
- c. 476-550 Aryabhata - utiliza un sistema de cifrado alfabético para los números que utilizan cero
- c. 598-670 Brahmagupta - explica el Numerales hindúes Árabe (sistema moderno número), que utiliza decimales enteros , enteros negativos y cero
- . c 780-850 Muhammad ibn Musa al-Ḵwārizmī - primero en exponer en algorismo fuera India
- c. 920-980 Abul Hasan Ahmad ibn Ibrahim Al-Uqlidisi - primer tratamiento matemático directa conocida de las fracciones decimales.
- c. 1300-1500 El Escuela de Kerala en Sur de la India - decimal Los números de coma flotante
- 1548 / 49-1620 Simon Stevin - autor de De Thiende ('la décima')
- 1561-1613 Bartholemaeus Pitiscus - (posiblemente) la notación decimal.
- 1550-1617 John Napier - uso de logaritmos decimales como una herramienta computacional
- 1765 Johann Heinrich Lambert - discute (con pocas o ninguna pruebas) patrones en expansiones decimales de números racionales y señala una conexión con el pequeño teorema de Fermat en el caso de los denominadores principales
- 1800 Karl Friedrich Gauss - utiliza la teoría de números para explicar sistemáticamente los patrones recurrentes en las expansiones decimales de números racionales (por ejemplo, la relación entre la longitud del período de la parte recurrente y el denominador, que fracciones con el mismo denominador tienen recurrentes partes decimales que son turnos de cada otro, como 1/7 y 2/7) y también plantea preguntas que siguen abiertas hasta el día (por ejemplo, un caso especial de La conjetura de Artin sobre las raíces primitivas: es 10 un generador módulo p para infinitos primos p)?.
- 1925 Louis Charles Karpinski - La Historia de la aritmética
- 1959 Werner Buchholz - dedos o puños? (La elección de representación decimal o binario)
- 1974 Hermann Schmid - Cálculo Decimal
- 2000 Georges Ifrah - La Historia universal de las cifras: desde la Prehistoria hasta la invención de la computadora
- 2003 Mike Cowlishaw - Decimal Floating-Point: algoritmo para ordenadores.
Los lenguajes naturales
Un sistema decimal sencillo, en el que 11 se expresa hasta diez-ona y 23 ya que dos-ten-tres, se encuentra en idiomas chino excepto Wu, y en Vietnamita con algunas irregularidades. Japonés, Coreano, y Tailandesa haber importado el sistema decimal chino. Muchos otros idiomas con un sistema decimal tienen palabras especiales para los números entre el 10 y el 20, y décadas.
Idiomas incas como Quechua y Aymara tiene un sistema decimal casi sencillo, en el que 11 se expresa como diez con uno y 23 como dos hasta diez con tres.
Algunos psicólogos sugieren irregularidades de números en un lenguaje puede obstaculizar la capacidad de conteo de los niños.