Contenido Checked

Conjunto de Mandelbrot

Temas relacionados: Matemáticas

Antecedentes

SOS Children ha intentado que el contenido de Wikipedia más accesible por esta selección escuelas. Infantil SOS es la mayor donación de caridad del mundo niños huérfanos y abandonados de la oportunidad de la vida familiar.

Imagen inicial de una secuencia de conjunto de Mandelbrot zoom con ambiente de color continuamente

El conjunto de Mandelbrot es un conjunto de los puntos en el plano complejo , la límite de los cuales forma un fractal . Matemáticamente, el conjunto de Mandelbrot se puede definir como el conjunto de-valores complejos c para el cual el órbita de 0 bajo iteración de la complejo cuadrática polinomio x n + 1 = x n 2 + c restos delimitada.

Ej. c = 1 da la secuencia 0, 1, 2, 5, 26 ... que conduce hasta el infinito. Como esta secuencia es ilimitada, 1 no es un elemento del conjunto de Mandelbrot.

Por otra parte, c = i da la secuencia 0, i, (-1 + i), -i, (-1 + i), -i ... que está limitada, y por lo tanto pertenece a la Mandelbrot.

Cuando calculado y representado gráficamente en el plano complejo, el Conjunto de Mandelbrot se ve que tiene un límite elaborada, que no simplifica en cualquier ampliación dada. Esto califica el límite como un fractal.

El conjunto de Mandelbrot se ha convertido fuera populares matemáticas tanto por su atractivo estético y por ser una estructura complicada que surge de una simple definición. Benoît Mandelbrot y otros trabajaron duro para comunicar esta área de las matemáticas al público.

Historia

El conjunto de Mandelbrot tiene su lugar en dinámicas complejas, un campo investigaron por primera vez por los matemáticos franceses Pierre Fatou y Gaston Julia en el comienzo del siglo 20a. Las primeras fotos de ella se extrajeron en 1978 por Robert Brooks y Peter Matelski como parte de un estudio de Grupos kleinianos.

Mandelbrot estudió el espacio de parámetros de polinomios de segundo grado en un artículo que apareció en 1980. El estudio matemático del conjunto de Mandelbrot realmente comenzó con el trabajo de los matemáticos Adrien Douady y John H. Hubbard, que estableció muchas de sus propiedades fundamentales y nombró el conjunto en honor de Mandelbrot.

Los matemáticos Heinz-Otto Peitgen y Peter Richter llegó a ser bien conocido por promover el set con brillantes fotografías, libros, y una galería de gira.

El artículo de portada de la 08 1985 Scientific American ofreció una imagen creada por Mandelbrot, Peitgen, y Hubbard.

El trabajo de Douady y Hubbard coincidió con un gran aumento en el interés por la dinámica compleja y matemáticas abstractas, y el estudio del conjunto de Mandelbrot ha sido una pieza central de este campo desde entonces. Una lista exhaustiva de todos los matemáticos que han contribuido a la comprensión de este conjunto desde entonces está más allá del alcance de este artículo, pero dicha lista incluirá en especial Mikhail Lyubich,, Curt McMullen, John Milnor, Mitsuhiro Shishikura, y Jean-Christophe Yoccoz.

Definición formal

El conjunto de Mandelbrot M se define por una familia de complejo polinomios de segundo grado

P_c: \ mathbb C \ a \ mathbb C

dada por

P_c: z \ mapsto z ^ 2 + c ,

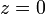donde c es un parámetro complejo. Para cada c , Se tiene en cuenta el comportamiento de la secuencia (0, p_c (0), p_c (p_c (0)), p_c (p_c (p_c (0))), \ ldots) obtenido por iteración P_c (z) a partir de punto crítico z = 0 \, , Que o bien se escapa al infinito o se mantiene dentro de un disco de algún radio finito. El conjunto de Mandelbrot se define como el conjunto de todos los puntos c de tal manera que la secuencia anterior no escapa al infinito.

Representación de un matemático del conjunto de Mandelbrot M, un punto c es de color negro si pertenece al conjunto, y blanco en caso contrario. Re [c] y Im [c] denotan las partes real e imaginaria de c.

Más formalmente, si P_c ^ {\ circ} n (z) denota la enésima iteración de P_c (z) (Es decir, P_c (z) compuesto con sí n veces), el conjunto de Mandelbrot es el subconjunto de la plano complejo dada por

M = \ left \ {c \ in \ mathbb C: \ sup_ {n \ in \ mathbb N} | p_c ^ {\ circ} n (0) | <\ infin \ right \}.

Matemáticamente, el conjunto de Mandelbrot es sólo una un conjunto de números complejos. Un número complejo dado c o bien pertenece a M o no lo hace. Una imagen del conjunto de Mandelbrot se puede hacer por la coloración de todos los puntos c que pertenecen a M negro, y todos los demás puntos de blanco. Las imágenes más coloridas por lo general visto son generados por puntos para colorear no en el conjunto de acuerdo con la rapidez o lentitud de la secuencia | P_c ^ {\ circ} n (0) | diverge a infinito. Vea la sección de dibujos de computadora abajo para más detalles.

El conjunto de Mandelbrot también se puede definir como la locus conexión de la familia de polinomios P_c (z) . Es decir, es el subconjunto del plano complejo que consiste en esos parámetros c para los cuales el Julia conjunto de P_c es conectada.

Propiedades básicas

El conjunto de Mandelbrot es un conjunto compacto , que figura en el disco cerrado de radio 2 alrededor del origen. De hecho, un punto c pertenece al conjunto de Mandelbrot si y sólo si | P_c ^ {\ circ} n (0) | \ leq 2 para todos n \ geq 0 . En otras palabras, si el valor absoluto de P_c ^ {\ circ} n (0) nunca se hace mayor que 2, la secuencia se escapará al infinito.

Correspondencia entre el conjunto de Mandelbrot y la mapa logístico

La intersección de M con el eje real es precisamente el intervalo [-2, 0,25] \, . Los parámetros a lo largo de este intervalo se pueden poner en uno-a-uno correspondencia con los de la verdadera familia logística,

z \ mapsto \ lambda z (1-z), \ quad \ lambda \ in [1,4]. \,

La correspondencia está dada por

c = \ frac {1 - (\ lambda 1) ^ 2} {4}.

De hecho, esto da una correspondencia entre todo el espacio de parámetros de la familia logística y la del conjunto de Mandelbrot.

El área del conjunto de Mandelbrot se estima en 1.506 591 77 0.000 000 ± 08.

Douady y Hubbard han demostrado que el conjunto de Mandelbrot es conectada. De hecho, construyeron una explícita isomorfismo conformal entre el complemento del conjunto Mandelbrot y el complemento de la disco unidad cerrada. Mandelbrot había conjeturado en un principio que el conjunto de Mandelbrot está desconectado. Esta conjetura se basa en imágenes de ordenador generados por los programas que no son capaces de detectar los filamentos delgados que conectan las diferentes partes de M . Tras más experimentos, revisó su conjetura, decidiendo que M debería estar conectado.

La fórmula dinámica para la uniformización del complemento del conjunto de Mandelbrot, que surge de la prueba Douady y de Hubbard de la conexión de M , Da lugar a rayos externos del conjunto de Mandelbrot. Estos rayos pueden usarse para estudiar el conjunto de Mandelbrot en términos combinatorios y formar la columna vertebral de la Parapuzzle Yoccoz.

La frontera del conjunto de Mandelbrot es exactamente el locus bifurcación de la familia cuadrática; es decir, el conjunto de parámetros c para los cuales la dinámica cambia abruptamente bajo pequeños cambios de c. Puede ser construido como el conjunto límite de una secuencia de curvas algebraicas planas, las curvas de Mandelbrot, del tipo general conocido como lemniscates polinómicas. Las curvas de Mandelbrot se definen mediante el establecimiento de p = 0 z, p n = n-1 + 2 z p, y luego interpretar el conjunto de puntos | n p (z) | = 1 en el plano complejo como una curva en el verdadero cartesiano plano de grado 2 n + 1 en x e y.

Otras propiedades

Los principales focos cardioides y período

Los períodos de componentes hiperbólicos

Al mirar un cuadro de conjunto de Mandelbrot, uno inmediatamente nota la gran cardioide en forma de región en el centro. Este cardioide principal es la región de los parámetros c para cual P_c tiene una la atracción de punto fijo. Se compone de todos los parámetros de la forma

c = \ frac {1 - (\ mu-1) ^ 2} {4}

para algunos \ Mu \, en el disco unidad abierto.

A la izquierda de la cardioide principal, unida a ella en el punto c = -3/4 , Una bombilla de forma circular es visible. Esta bombilla está conformado por aquellos parámetros c \, para cual P_c tiene una atraer ciclo de periodo 2. Este conjunto de parámetros es un círculo real, la de radio cuarto alrededor de -1.

Hay infinitamente muchas otras bombillas tangente a la cardioide principal: por cada número racional \ Frac {p} {q} , Con p y q primos entre sí, hay una bombilla de tal manera que es tangente en el parámetro

c _ {\ frac {p} {q}} = \ frac {1 - \ left (e ^ {2 \ pi i \ frac {p} {q}} - 1 \ right) ^ 2} {4}.
Atraer ciclo en 2/5 de bulbo dibujan en el conjunto de Julia (animación)

Esta bombilla se llama \ Frac {p} {q} -bulb del conjunto de Mandelbrot. Se compone de los parámetros que tienen un ciclo de atracción del período q y el número de rotación combinatoria \ Frac {p} {q} . Más precisamente, la q periódico Fatou componentes que contienen el ciclo atrayendo todo contacto en un punto común (comúnmente llamado el \ Alpha \, -punto fijo). Si etiquetamos estos componentes U_0, \ dots, U_ {q-1} en la orientación en sentido antihorario, entonces P_c mapea el componente U_j al componente U_ {j + p \, (\ operatorname {mod} q)} .

La atracción de los ciclos y conjuntos de Julia para los parámetros en los media, 3/7, 2/5, 1/3, 1/4, 1/5 y bombillas

El cambio de comportamiento que ocurren en c _ {\ frac {p} {q}} que se conoce como una bifurcación: el punto fijo "choca" con la atracción de un período de repulsión q-ciclo. Al pasar a través del parámetro de bifurcación en el \ Frac {p} {q} -bulb, el punto fijo atraer convierte en un punto de repulsión fijo (el \ Alpha punto -fixed), y el periodo q -Ciclo convierte atraer.

Componentes hiperbólicos

Todas las bombillas que nos encontramos en la sección anterior fueron componentes interiores del conjunto de Mandelbrot en la que los mapas P_c \, tener un ciclo periódico de atracción. Tales componentes se denominan componentes hiperbólicos.

Se conjetura que estas son las únicas regiones del interior del M . Este problema, conocido como la densidad de hiperbolicidad, puede ser el problema abierto más importante en el campo de la dinámica compleja. Componentes no hiperbólicas hipotéticos del conjunto de Mandelbrot se refieren a menudo como componentes "queer".

Para polinomios cuadráticos reales, esta pregunta fue respondida positivamente en la década de 1990 de forma independiente por Lyubich y por Graczyk y Świątek. (Tenga en cuenta que los componentes hiperbólicos de intersección del eje real se corresponden exactamente con las ventanas periódicas en el Diagrama de Feigenbaum. Así que este resultado indica que existen esas ventanas cerca de todos los parámetros en el diagrama.)

No todos los componentes hiperbólico se puede llegar en una secuencia de bifurcaciones directas del cardioide principal del conjunto de Mandelbrot. Sin embargo, un componente de este tipo se puede llegar en una secuencia de bifurcaciones directos de la cardioide principal de una pequeña copia de Mandelbrot (ver más abajo).

Conectividad local

Se conjetura que el conjunto de Mandelbrot es conectado localmente. Esta famosa conjetura se conoce como MLC (por Mandelbrot localmente conectado). Por el trabajo de Adrien Douady y John H. Hubbard, esta conjetura se traduciría en un simple modelo abstracto "disco pellizcado" del conjunto de Mandelbrot. En particular, ello implicaría la conjetura hiperbolicidad importante antes mencionado.

La célebre obra de Jean-Christophe Yoccoz establece la conectividad local del conjunto de Mandelbrot en todo finito-renormalizable parámetros; es decir, en términos generales aquellas contenidas sólo en un número finito de copias pequeñas Mandelbrot. Desde entonces, la conectividad local se ha demostrado en muchos otros puntos de M , Pero la conjetura completa todavía está abierta.

Autosemejanza

Auto similitud en el conjunto de Mandelbrot muestra por el zoom en una partida especial durante la exploración en la dirección negativa-X. Las sartenes de centros de pantalla (-1,0) a (-1.31,0) mientras que la vista magnifica de 0,5 x 0,5 a 0,12 x 0,12 para aproximar la Relación Feigenbaum \ Delta .
Autosemejanza alrededor del punto -.1011 + .9563i Misiurewicz.

El conjunto de Mandelbrot es auto-similar con una lupa en los barrios de la Puntos Misiurewicz. También se conjetura para ser auto-similar alrededor generalizada Puntos Feigenbaum (por ejemplo, -1.401155 o -.1528 + 1.0397i), en el sentido de la convergencia a un conjunto límite.

Cuasi-auto-similitud en el conjunto de Mandelbrot

El conjunto de Mandelbrot, en general, no es estrictamente auto-similar pero es-auto-similar cuasi, como pequeñas versiones ligeramente diferentes de sí mismo se pueden encontrar en arbitrariamente pequeñas escalas.

Las pequeñas copias del conjunto de Mandelbrot son ligeramente diferentes, sobre todo por los finos hilos que los unen al cuerpo principal del conjunto.

Otros resultados

La Dimensión de Hausdorff de la frontera del conjunto Mandelbrot es igual a 2 tal como se determina por un resultado de Mitsuhiro Shishikura. No se sabe si la frontera del conjunto de Mandelbrot tiene planar positivo Medida de Lebesgue.

En el Modelo Blum-Shub-Smale de cálculo real, el conjunto de Mandelbrot no es computable, sino su complemento es computablemente enumerable. Sin embargo, muchos objetos simples (por ejemplo, la gráfica de exponenciación) tampoco son computables en el modelo de BSS. En la actualidad se desconoce si el conjunto de Mandelbrot es computable en modelos de computación real basado en análisis computable, que corresponden más a la noción intuitiva de "conspirar el conjunto por una computadora." Hertling ha demostrado que el conjunto de Mandelbrot es computable en este modelo si la conjetura hiperbolicidad es cierto.

Relación con los conjuntos de Julia

Un "conjunto de Julia incorporado"

Como consecuencia de la definición del conjunto de Mandelbrot, existe una estrecha correspondencia entre la geometría del conjunto de Mandelbrot en un punto dado y la estructura de la correspondiente Conjunto de Julia.

Este principio se explota en los resultados de prácticamente todos profundas en el conjunto de Mandelbrot. Por ejemplo, Shishikura demuestra que, para un conjunto denso de los parámetros en el límite del conjunto de Mandelbrot, el conjunto de Julia tiene Hausdorff dimensión dos, y a continuación, transfiere esta información al plano parámetro. Del mismo modo, Yoccoz demuestra por primera vez la conectividad local de conjuntos de Julia, antes de establecer que para el conjunto de Mandelbrot en los parámetros correspondientes. Adrien Douady Frases este principio como

Plough en el plano dinámico, y la cosecha en el espacio de parámetros.

Geometría

períodos del ciclo y las antenas

Recordemos que, para cada número racional \ Frac {p} {q} , Donde p y q son primos entre sí, hay un componente hiperbólico de período q bifurcación de la cardioide principal. La parte del conjunto de Mandelbrot conectado a la cardioide principal en este punto de bifurcación se denomina p / q-extremidad. Experimentos ordenador sugieren que el diámetro de la extremidad tiende a cero como \ Frac {1} {q ^ 2} . La mejor estimación actual conocido es el famoso Yoccoz-desigualdad, que establece que el tamaño tiende a cero como \ Frac {1} {q} .

Un período q -limb tendrá q-1 "Antenas" en la parte superior de su extremidad. De este modo podemos determinar el período de una bombilla de determinada contando estas antenas.

Las generalizaciones

"Id =" "style =" mwe_player_0 ancho: 200px; altura: 200px "> Archivo: Multibrot.ogg 
Multibrot d ajusta con el cambio de 0 a 8

A veces, el loci conexión de las familias distintas de la familia cuadrática también se conoce como el Mandelbrot fija de estas familias.

El loci conectividad de las familias de polinomios unicritical F_C = z ^ d + c \, para d> 2 a menudo son llamados conjuntos Multibrot.

Conjuntos Multibrot de grados 3 y 4

Para las familias generales de funciones holomorfas, la frontera del conjunto de Mandelbrot se generaliza a la locus de bifurcación, que es un objeto natural para estudiar incluso cuando el locus conexión no es útil.

También es posible considerar construcciones similares en el estudio de las asignaciones no analíticos. De particular interés es la tricornio, el locus de la conectividad de la familia contra el holomorfa

z \ mapsto \ bar {z} ^ 2 + c. \,

El tricornio (también llamado a veces el conjunto Mandelbar) se encontró por Milnor en su estudio de las rebanadas de parámetros de polinomios cúbicos reales. No está conectada localmente. Esta propiedad se hereda por el locus conexión de polinomios cúbicos reales.


Dibujos de ordenador

Método Buddhabrot
Imagen fija de una película de aumentar la magnificación en ,001643721971153 + 0.822467633298876i

Algoritmos:

  • Escapar algoritmo de tiempo
    • versión boolean (dibuja establece M-y su exterior por medio de 2 colores) = algoritmo de Mandelbrot
    • discreta (entero) version = método de ajuste de nivel (LSM / M); dibuja Mandelbrot y de color bandas en su exterior
    • versión continua
    • versión curvas de nivel = atrae lemniscates de Mandelbrot = límites de conjuntos de nivel
    • descomposición del exterior del conjunto de Mandelbrot
  • potencial complejo
    • Hubbard-Douady (real) potencial del conjunto de Mandelbrot (CPM / M) - parte radial del potencial complejo
    • ángulo externo del conjunto de Mandelbrot - parte angular del potencial complejo
    • abstracto M-set
  • Método de estimación Distancia de conjunto de Mandelbrot
  • algoritmo utilizado para explorar el interior del conjunto de Mandelbrot
    • período de componentes hiperbólicos
    • multiplicador de la órbita periódica (rayos internos (ángulo) y el radio INTENAL)
    • bof61 y bof60

Cada algoritmo puede ser implementado en secuencial o versión paralela. Simetría de espejo se puede utilizar para cálculos de velocidad-up .

Wikibooks tiene un libro sobre el tema de: Fractales

Escapar algoritmo de tiempo

El algoritmo más simple para generar una representación del conjunto de Mandelbrot se conoce como el algoritmo de "escapar de tiempo". Un cálculo de repetición se realiza para cada x, punto y en el área de trazado y basado en el comportamiento de ese cálculo, se elige un color para ese píxel.

El x e y ubicación de cada punto se utilizan como valores iniciales en una repetición, o iteración de cálculo (descrito en detalle a continuación). El resultado de cada iteración se utiliza como los valores de partida para la siguiente. Los valores se comprueban durante cada iteración para ver si han llegado a un estado crítico 'escape'. Si se alcanza esa condición, el cálculo se detiene, el píxel se dibuja, y los próximos x, se examina el punto y. Para algunos valores de partida, escape se produce rápidamente, después de sólo un pequeño número de iteraciones. Para otros valores de partida, puede tardar cientos o miles de iteraciones para escapar. Para los valores dentro del conjunto de Mandelbrot, nunca ocurrirá escape. El programador o usuario debe elegir la cantidad de iteraciones, o "profundidad", que desean examinar. Cuanto mayor es el número máximo de iteraciones, más detalles y sutileza emergen en la imagen final, pero el tiempo que se necesita para calcular la imagen.

El color de cada punto representa la rapidez con que los valores alcanzaron el punto de escape. A menudo negro se utiliza para mostrar valores que no logran escapar antes de que el límite de iteración, y colores más brillantes gradualmente se utilizan para los puntos que se escapan. Esto da una representación visual de cuántos ciclos se requiere antes de llegar a la condición de escape.

Para los programadores

La definición del conjunto de Mandelbrot, junto con sus propiedades básicas, sugiere un algoritmo simple para hacer un dibujo del conjunto de Mandelbrot. La región del plano complejo que estamos considerando se subdivide en un cierto número de píxeles. Para colorear cualquier pixel, y mucho c \, ser el punto medio de ese píxel. Ahora Iteramos el valor crítico c \, bajo P_c \, , Comprobando en cada etapa si el punto de la órbita tiene un módulo mayor que 2.

Si este es el caso, sabemos que el punto medio no pertenece al conjunto de Mandelbrot, y coloreamos nuestra píxel. (De cualquier coloreamos de blanco para obtener la imagen matemática simple o colorearlo según el número de iteraciones que se utilizan para obtener las imágenes de colores conocidos). De lo contrario, seguimos iterando para cierto (grande, pero fijo) número de pasos, después de lo cual decidimos que nuestro parámetro es "probablemente" en el conjunto de Mandelbrot, o al menos muy cerca de ella, y el color del píxel negro.

En pseudocódigo, este algoritmo se vería de la siguiente manera. 

 Para cada píxel de la pantalla hacer: {x = x0 = coordenada X del píxel y = y0 = coordenada de iteración pixel = 0 max_iteration = 1,000, mientras que (x * x + y * y <= (2 * 2 ) Y iteración <max_iteration) {xtemp = x * x - y * y + x0 y = 2 * x * y + x = y0 xtemp iteración = iteración + 1} if (iteración == max_iteration) luego de color = color negro persona = iteración parcela (x0, y0, color)}

donde, relacionando el pseudocódigo para c \,, z \, y P_c \, :

  • z = x + iy
  • z ^ 2 = x ^ 2 + i2xy - y ^ 2
  • c = x0 + iy0

y así, como se puede ver en el pseudocódigo en el cálculo de x e y:

  • x = Re (z ^ 2 + c) = x ^ 2-y ^ 2 + x0 y y = Im (z ^ 2 + c) = 2xy + y0

Para obtener imágenes a color del conjunto, la asignación de un color a cada valor del número de iteraciones ejecutadas se puede hacer utilizando una de una variedad de funciones (lineal, exponencial, etc.). Una forma práctica de hacerlo, sin ralentizar los cálculos, es utilizar el número de iteraciones ejecutadas como una entrada a una tabla de la paleta de colores de consulta inicializado en el arranque. Si la tabla de colores tiene, por ejemplo, 500 entradas, entonces usted puede utilizar n mod 500, donde n es el número de iteraciones, para seleccionar el color que desea utilizar. Puede inicializar la matriz de la paleta de colores de varias maneras diferentes, dependiendo de qué característica especial de la conducta de escape se desea destacar gráficamente.

Continuo colorante (liso)

Esta imagen se hizo con el escape algoritmo de tiempo. Note las "bandas" muy evidentes de color.
Esta imagen se hizo con la iteración Normalizado Conde Algoritmo. Note las bandas de color han sido sustituidos por un degradado suave.
Otro ejemplo de la iteración Normalized Count algoritmo. Observe que no hay efecto de bandas; todos los colores fluyen entre sí. Además, los colores toman en el mismo patrón que se observaría si se utilizó el algoritmo de tiempo de escape.

El Escape Algoritmo El tiempo es popular por su simplicidad. Sin embargo, crea bandas de color, que pueden desvirtuar el valor de una imagen. Esto se puede solucionar mediante el Normalizada número de iteraciones del algoritmo, que ofrece una suave transición de colores entre iteraciones. La ecuación es

n + \ frac {\ ln (2 \ ln (B)) - \ ln (\ ln (| z |))} {\ ln (P)}

donde n es el número de iteraciones para z, B es el radio de rescate (normalmente es 2 para un conjunto de Mandelbrot, pero puede ser cambiado), y P es la potencia para la que z se eleva a en la ecuación de conjunto de Mandelbrot (z n = 1 z n P + c, P es generalmente 2). Otra ecuación para esto es

n + 1- \ frac {\ ln (\ ln (| z |))} {\ ln (2)}.

Tenga en cuenta que esta nueva ecuación es más sencilla que la primera, pero sólo funciona para los conjuntos de Mandelbrot con un radio de rescate de 2 y una potencia de 2.
Mientras que este algoritmo es relativamente fácil de implementar (usando la ecuación), hay algunas cosas que deben ser tomados en consideración. En primer lugar, las dos ecuaciones devuelven un flujo continuo de números. Sin embargo, es hasta usted para decidir sobre cómo los valores de retorno se convertirán en un color. Algún tipo de método para la fundición de estos números en un gradiente debe desarrollarse. En segundo lugar, se recomienda que una pocas iteraciones adicionales se realizan de modo que z puede crecer. Si deja de iterar tan pronto como se escapa z, existe la posibilidad de que el algoritmo de suavizado no funcionará.

La distancia estimada

Se puede calcular la distancia desde el punto c (en exterior o interior) a punto de la más cercana límite del conjunto de Mandelbrot.

Estimación de la distancia exterior

La prueba de la conexión del conjunto de Mandelbrot, de hecho, da una fórmula para la uniformizar mapa de la complemento de M (Y el derivado de este mapa). Por el Koebe cuarto teorema, uno puede entonces estimar la distancia entre el punto medio de nuestra pixel y el conjunto de Mandelbrot hasta un factor de 4.

En otras palabras, siempre que el número máximo de iteraciones es suficientemente alta, se obtiene una imagen de la Mandelbrot con las siguientes propiedades:

  1. Cada pixel que en algún punto del conjunto de Mandelbrot es de color negro.
  2. Cada píxel que es de color negro está cerca del conjunto de Mandelbrot.
Estimación de la distancia exterior puede ser utilizado para dar color a toda complemento del conjunto de Mandelbrot

La estimación de la distancia de un c píxeles (un número complejo) a partir del conjunto de Mandelbrot está dada por

b = \ lim_ {n \ to \ infty} 2 \ cdot \ ln (\ mediados {p_c ^ {\ circ} n (c)} \ mediados) \ cdot \ frac {\ {mediados p_c ^ {\ circ} n ( c)} \ mediados} {\ mid \ frac {\ partial} {\ partial {c}} p_c ^ {\ circ} n (c) \ mediados}

donde

  • P_c (z) \, representa complejo polinomio cuadrático
  • P_c ^ {\ circ} n (c) representa n iteraciones de P_c (z) \ az o z ^ 2 + c \ az , Comenzando con z = c: P_c ^ {\ circ 0} (c) = c , P_c ^ {\ circ n + 1} (c) = p_c ^ {\ circ n} (c) ^ 2 + c ;
  • \ Frac {\ partial} {\ partial {c}} p_c ^ {\ circ} n (c) es la derivada de P_c ^ {\ circ} n (c) con respecto a c. Este derivado se puede encontrar a partir de \ Frac {\ partial} {\ partial {c}} p_c ^ {\ circ 0} (c) = 1 y luego \ Frac {\ partial} {\ partial {c}} p_c ^ {\ circ n + 1} (c) = 2 \ cdot {} p_c ^ {\ circ} n (c) \ cdot \ frac {\ partial} { \ partial {c}} p_c ^ {\ circ} n (c) + 1 . Esto puede verificarse fácilmente mediante el uso de la regla de la cadena para la derivada.

Desde el punto de vista matemático, esta fórmula sólo funciona en el límite donde n tiende a infinito, pero las estimaciones muy razonables se puede encontrar con sólo unas pocas iteraciones adicionales después de las principales salidas de bucle.

Una vez b se encuentra, por el Koebe cuarto teorema, sabemos que no tiene sentido del conjunto de Mandelbrot con la distancia de c menor que b / 4.

Estimación de la distancia Interior

Píxeles de color de acuerdo a la distancia interior estimado

También es posible estimar la distancia de un (es decir, interior) punto limitly periódica a la frontera del conjunto Mandelbrot. La estimación está dada por b = \ frac {1- \ mediados {\ frac {\ partial} {\ partial {z}} p_c ^ {\ circ} p (z_0)} \ mediados ^ 2} {\ mediados {\ frac {\ partial} { \ partial {c}} \ frac {\ partial} {\ partial {z}} p_c ^ {\ circ} p (z_0) + \ frac {\ partial} {\ partial {z}} \ frac {\ partial} { \ partial {z}} p_c ^ {\ circ} p (z_0) \ frac {\ frac {\ partial} {\ partial {c}} p_c ^ {\ circ} p (z_0)} {1- \ frac {\ parcial} {\ partial {z}} p_c ^ {\ circ} p (z_0)}} \ mediados}

donde

  • p es el período,
  • c es el punto de ser estimado,
  • P_c (z) es el complejo polinomio cuadrático P_c (z) = z ^ 2 + c
  • P_c ^ {\ circ} p (z_0) es p composiciones de P_c (z) \ az , Empezando con P_c ^ {\ circ 0} (z) = z_0
  • z_0 es cualquiera de las p puntos que hacen que la atractor de las iteraciones de P_c (z) \ az empezando con P_c ^ {\ circ 0} (z) = c ; z_0 satisface z_0 = p_c ^ {\ circ} p (z_0) ,
  • \ Frac {\ partial} {\ partial {c}} \ frac {\ partial} {\ partial {z}} p_c ^ {\ circ} p (z_0) , \ Frac {\ partial} {\ partial {z}} \ frac {\ partial} {\ partial {z}} p_c ^ {\ circ} p (z_0) , \ Frac {\ partial} {\ partial {c}} p_c ^ {\ circ} p (z_0) y \ Frac {\ partial} {\ partial {z}} p_c ^ {\ circ} p (z_0) son diversos derivados de P_c ^ {\ circ} p (z) , Evaluada en z_0 .

Dado p y z_0 , P_c ^ {\ circ} p (z_0) y sus derivados pueden ser evaluados por:

  • \ Begin {align} \ frac {\ partial} {\ partial {c}} \ frac {\ partial} {\ partial {z}} p_c ^ {\ circ 0} (z_0) = & 0 \\ \ frac {\ parcial} {\ partial {z}} \ frac {\ partial} {\ partial {z}} p_c ^ {\ circ 0} (z_0) = & 0 \\ \ frac {\ partial} {\ partial {c}} p_c ^ {\ circ 0} (z_0) = & 0 \\ \ frac {\ partial} {\ partial {z}} p_c ^ {\ circ 0} (z_0) = & 1 \\ p_c ^ {\ circ 0} (z_0) = & z_0 \ end {align}
  • \ Begin {align} \ frac {\ partial} {\ partial {c}} \ frac {\ partial} {\ partial {z}} p_c ^ {\ circ n + 1} (z_0) & = 2 \ cdot (\ frac {\ partial} {\ partial {c}} p_c ^ {\ circ} n (z_0) \ cdot \ frac {\ partial} {\ partial {z}} p_c ^ {\ circ} n (z_0) + p_c ^ {\ circ} n (z_0) \ cdot \ frac {\ partial} {\ partial {c}} \ frac {\ partial} {\ partial {z}} p_c ^ {\ circ} n (z_0)) \\ \ frac {\ partial} {\ partial {z}} \ frac {\ partial} {\ partial {z}} p_c ^ {\ circ n + 1} (z_0) & = 2 \ cdot (\ frac {\ partial} { \ partial {z}} p_c ^ {\ circ} n (z_0) ^ 2 + p_c ^ {\ circ} n (z_0) \ cdot \ frac {\ partial} {\ partial {z}} \ frac {\ partial} {\ partial {z}} p_c ^ {\ circ} n (z_0)) \\ \ frac {\ partial} {\ partial {c}} p_c ^ {\ circ n + 1} (z_0) & = 2 \ cdot p_c ^ {\ circ} n (z_0) \ cdot \ frac {\ partial} {\ partial {c}} p_c ^ {\ circ} n (z_0) + 1 \\ \ frac {\ partial} {\ partial {z }} p_c ^ {\ circ n + 1} (z_0) & = 2 \ cdot p_c ^ {\ circ} n (z_0) \ cdot \ frac {\ partial} {\ partial {z}} p_c ^ {\ circ n } (z_0) \\ p_c ^ {\ circ n + 1} (z_0) & = p_c ^ {\ circ} n (z_0) ^ 2 + c \ end {align} .

Análoga a la caja exterior, una vez b se encuentra, sabemos que todos los puntos dentro de la distancia de b / 4 de c se encuentran dentro del conjunto de Mandelbrot.

Hay dos problemas prácticos con la estimación de la distancia interior: en primer lugar, tenemos que encontrar z_0 Precisamente, y en segundo lugar, tenemos que encontrar p con precisión. El problema con z_0 es que la convergencia de z_0 iterando P_c (z) requiere, en teoría, un número infinito de operaciones. El problema con período es que, a veces, debido a errores de redondeo, un período se identifica falsamente a ser un múltiplo entero del período real (por ejemplo, se detecta un período de 86, mientras que el período real es sólo 43 = 86/2) . En tal caso, la distancia se sobreestima, es decir, el radio reportado podría contener puntos fuera del conjunto de Mandelbrot.

Vista 3D: valor absoluto de la órbita de los puntos interiores del conjunto de Mandelbrot

Optimizaciones

Una forma de mejorar los cálculos es averiguar de antemano si el punto dado se encuentra dentro de la cardioide o en el bulbo período de 2.

Para evitar tener que hacer un gran número de iteraciones para otros puntos en el conjunto, se puede hacer "periodicidad comprobación" significa -de qué comprobar si se ha alcanzado un punto alcanzado en la iteración un píxel antes. Si es así, el píxel no puede divergen, y debe estar en el conjunto. Esto es más relevante para los cálculos de punto fijo, donde existe una probabilidad relativamente alta de dicha periodicidad -un completo de punto flotante (o de mayor precisión) aplicación sería rara vez entrar en un período tan.

Periodicidad de cheques es, por supuesto, una solución de compromiso: La necesidad de recordar los puntos cuesta instrucciones de memoria y de gestión de datos, mientras que ahorra instrucciones computacionales

Recuperado de " http://en.wikipedia.org/w/index.php?title=Mandelbrot_set&oldid=208950518 "