
Significar
Antecedentes
Este contenido de Wikipedia ha sido seleccionada por SOS para su utilización en las escuelas de todo el mundo. Haga clic aquí para obtener información sobre el apadrinamiento de niños.
En las estadísticas , la media tiene dos significados relacionados:
- la media aritmética (y se distingue de la media geométrica o media armónica).
- la valor esperado de una variable aleatoria , que también se llama media de la población.
A veces se dice que la 'media' significa promedio. Esto es incorrecto si "media" se toma en el sentido específico de "media aritmética", ya que hay diferentes tipos de medias: la media, la mediana y el modo . Por ejemplo, los precios medios de la vivienda casi siempre utilizan el valor de la mediana de la media.
Para una de valor real variable aleatoria X, la media es la expectativa de X. Tenga en cuenta que no todos los distribución de probabilidad tiene un medio definido (o varianza ); ver el Distribución de Cauchy para un ejemplo.
Para conjunto de datos, la media es la suma de las observaciones dividido por el número de observaciones. La media es citado a menudo junto con la desviación estándar : la media describe la ubicación central de los datos, y la desviación estándar describe la propagación.
Una medida alternativa de dispersión es la desviación media, equivalente a la media desviación absoluta de la media. Es menos sensible a los valores atípicos, pero menos matemáticamente tratable.
Así como estadísticas, los medios se utilizan a menudo en la geometría y el análisis; una amplia gama de medios se han desarrollado a estos efectos, que no se utilizan mucho en las estadísticas. Estos se enumeran a continuación.
Ejemplos de medios
Media aritmética
La media aritmética es el promedio "estándar", a menudo llamado simplemente el "medio".
La media a menudo puede confundirse con el medio o modo . La media es la media aritmética de un conjunto de valores, o de distribución; Sin embargo, para distribuciones asimétricas, la media no es necesariamente el mismo que el valor medio (mediana), o la más probable (modo). Por ejemplo, el ingreso medio está sesgado al alza por un pequeño número de personas con grandes ingresos, por lo que la mayoría tienen un ingreso inferior a la media. Por el contrario, la renta mediana es el nivel en el que la mitad de la población se encuentra por debajo y media está por encima. El ingreso modo es el ingreso más probable, y favorece el mayor número de personas con ingresos más bajos. La mediana o la moda son a menudo las medidas más intuitivas de estos datos.
Dicho esto, muchos distribuciones asimétricas se describen mejor por su media - tales como las exponenciales y Poisson distribuciones.
Por ejemplo, la media aritmética de 34, 27, 45, 55, 22, 34 (seis valores) es (34 + 27 + 45 + 55 + 22 + 34) / 6 = 217/6 ≈ 36.167.
Media geométrica
La media geométrica es un promedio que es útil para conjuntos de números que son interpretados de acuerdo con su producto y no su suma (como es el caso con la media aritmética). Por ejemplo, las tasas de crecimiento.
Por ejemplo, la media geométrica de 34, 27, 45, 55, 22, 34 (seis valores) es (34 × 27 × 45 × 55 × 22 × 34) 1/6 = 1/6 = 1699493400 34.545.
Media armónica
La media armónica es una media, que es útil para conjuntos de números que se definen en relación con algunos unidad, por ejemplo velocidad (distancia por unidad de tiempo).
Por ejemplo, la media armónica de los números 34, 27, 45, 55, 22, y 34 es
Medios generalizadas
Potencia media
La media generalizada, también conocida como la potencia media o titular quiere decir, es una abstracción de la cuadrática, aritmética, geométrica y medias armónicas. Se define por
Al elegir el valor adecuado para el parámetro m obtenemos
 | máximo |
 | media cuadrática, |
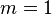 | media aritmética , |
 | media geométrica, |
 | armónica significa, |
 | mínimo. |
f-media
Esto se puede generalizar adicionalmente como la f-media generalizada
y de nuevo una elección adecuada de un invertible  dare
dare
 | armónica significa, |
 | potencia media, |
 | media geométrica. |
Media ponderada
La se utiliza media aritmética ponderada, si se quiere combinar los valores promedio de las muestras de la misma población con diferentes tamaños de muestra:
Los pesos  representar los límites de la muestra parcial. En otras aplicaciones que representan una medida de la fiabilidad de la influencia sobre la media por los valores respectivos.
representar los límites de la muestra parcial. En otras aplicaciones que representan una medida de la fiabilidad de la influencia sobre la media por los valores respectivos.
Media truncada
A veces un conjunto de números (el datos) podría estar contaminado por los valores atípicos inexactas, es decir, valores que son mucho demasiado baja o demasiado alta. En este caso se puede utilizar una media truncada. Se trata de descartes partes de los datos dado en la parte superior o la parte inferior, por lo general una cantidad igual en cada extremo, y luego tomando la media aritmética de los datos restantes. El número de valores eliminados se indica como un porcentaje del número total de valores.
Intercuartil significa
La intercuartil significa es un ejemplo específico de una media truncada. Es simplemente la media aritmética después de quitar el más bajo y el más alto trimestre de valores.
suponiendo que los valores se han ordenado.
La media de una función
En el cálculo , y especialmente cálculo multivariable, la media de una función es vagamente definido como el valor promedio de la función sobre su dominio. En una variable, la media de una función f (x) en el intervalo (a, b) se define por
(Ver también teorema del valor medio). En varias variables, la media durante un relativamente compacto dominio de U en un espacio euclidiano se define por
Esto generaliza la media aritmética. Por otro lado, también es posible generalizar la media geométrica a las funciones mediante la definición de la media geométrica de f para ser
Más en general, en teoría de la medida y la teoría de la probabilidad , ya sea clase de significar juega un papel importante. En este contexto, La desigualdad de Jensen pone estimaciones agudos sobre la relación entre estas dos nociones diferentes de la media de una función.
La media de los ángulos
La mayor parte de las vías habituales fallan en cantidades circulares, como ángulos , daytimes, fracciones de números reales . Para aquellas cantidades que necesita un media de cantidades circulares.
Otros medios
- Media aritmético-geométrica
- -Aritmética armónica media
- Media de Cesàro
- Media Chisini
- Media Contraharmonic
- Media simétrica Primaria
- Media geométrica-armónica
- Heinz significa
- Media heroniana
- Identric significar
- Media de mínimos cuadrados
- Lehmer significa
- Media logarítmica
- Mediana
- Media cuadrática
- Stolarsky significa
- Media Temporal
- Media geométrica ponderada
- Media armónica ponderada
- Entropía de Rényi (un f-media generalizada)
Propiedades
El método más general para la definición de una media o promedio, y, toma cualquier función de una lista g (x_1, x_2, ..., x_n), que es simétrico en virtud de permutación de los miembros de la lista, y equivale a la misma función con el valor de la media sustituyendo cada miembro de la lista: g (x_1, x_2, ..., x_n) = g (y, y, ..., y). Todos los medios comparten algunas propiedades y propiedades adicionales son compartidos por los medios más comunes. Algunas de estas propiedades se recogen aquí.
Media ponderada
A medias ponderada  es una función que mapea tuplas de números positivos a un número positivo (
es una función que mapea tuplas de números positivos a un número positivo (  ).
).
- " Punto fijo ":

- Homogeneidad:

- (Usando notación vectorial:
 )
)
- (Usando notación vectorial:
- Monotonía:

Sigue
- Acotación:
![\ Forall x \ M x \ in [\ min x, \ max x]](../../images/135/13510.png)
- Continuidad:

- Bosquejo de una prueba: Porque
 y
y  sigue
sigue  .
.
- Hay medios, que no son diferenciables . Por ejemplo, el número máximo de una tupla se considera un medio (como un caso extremo de la potencia media, o como un caso especial de una mediana ), pero no es diferenciable.
- Todos los medios enumerados anteriormente, con la excepción de la mayoría de las F-medios generalizadas, satisfacen las propiedades presentadas.
- Si
 es biyectiva, entonces el f-media generalizada satisface la propiedad del punto fijo.
es biyectiva, entonces el f-media generalizada satisface la propiedad del punto fijo. - Si
 es estrictamente monótona, entonces el f-media generalizada satisface también la propiedad monotonía.
es estrictamente monótona, entonces el f-media generalizada satisface también la propiedad monotonía. - En general un f-media generalizada se perderá la homogeneidad.
- Si
Estas propiedades implican técnicas para la construcción de medios más complejos:
Si  son medios ponderados,
son medios ponderados,  es un positivo número real , entonces
es un positivo número real , entonces 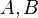 con
con
también son una media ponderada.
Media no ponderada
Intuitivamente hablado, una media no ponderada es una media ponderada con pesos iguales. Desde nuestra definición de medias ponderada anterior no exponga pesos particulares, la igualdad de pesos deben ser ejercidos por un camino diferente. Un punto de vista diferente sobre la ponderación homogénea es, que las entradas se pueden intercambiar sin alterar el resultado.
Así definimos  siendo una media no ponderada si es una media ponderada y para cada permutación
siendo una media no ponderada si es una media ponderada y para cada permutación  de entradas, el resultado es el mismo. Dejar
de entradas, el resultado es el mismo. Dejar  el conjunto de permutaciones de
el conjunto de permutaciones de  -tuplas.
-tuplas.
- Simetría:
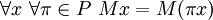
Análogamente a los medios ponderados, si  es una media ponderada y
es una media ponderada y  son medios ponderados,
son medios ponderados,  es un positivo número real , entonces
es un positivo número real , entonces 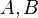 con
con
son también medios ponderados.
Convertir media no ponderada de medias ponderada
Una media no ponderada se puede convertir en una media ponderada por la repetición de elementos. Esta conexión también se puede utilizar para indicar que una media es la versión ponderada de una media no ponderada. Digamos que usted tiene la media no ponderada  y el peso de los números de los números naturales
y el peso de los números de los números naturales 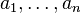 . (Si los números son racionales , entonces ellos multiplicar con el mínimo común denominador.) A continuación, la media ponderada correspondiente
. (Si los números son racionales , entonces ellos multiplicar con el mínimo común denominador.) A continuación, la media ponderada correspondiente  se obtiene por
se obtiene por
 .
.
Medios de tuplas de diferentes tamaños
Si una media  se define por tuplas de varios tamaños, entonces también se espera que la media de una tupla está limitada por los medios de particiones. Más precisamente
se define por tuplas de varios tamaños, entonces también se espera que la media de una tupla está limitada por los medios de particiones. Más precisamente
- Dada una tupla arbitraria
 , Cual es dividido en
, Cual es dividido en  , Entonces se cumple
, Entonces se cumple  . (Ver Casco convexo)
. (Ver Casco convexo)
La educación matemática
En muchos estándares del estado y del plan de estudios del gobierno, se espera que tradicionalmente los estudiantes a aprender bien el significado o la fórmula para el cálculo de la media en el cuarto grado. Sin embargo, en muchos , se alienta a los estándares basados en los planes de estudio de matemáticas de los estudiantes a inventar sus propios métodos, y no se les puede enseñar el método tradicional. Textos de reforma basado como TERC de hecho desalienta la enseñanza de la tradicional "añadir los números y se divide por el número de artículos" método a favor de pasar más tiempo en el concepto de la mediana , que no requiere la división. Sin embargo, la media se puede calcular con una simple calculadora de cuatro funciones, mientras que la mediana requiere un ordenador. La misma guía del profesor dedica varias páginas sobre cómo encontrar la mediana de un conjunto, que se juzga a ser más simple que la búsqueda de la media.
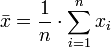
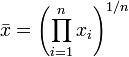


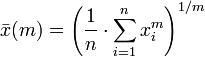

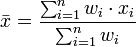


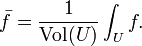

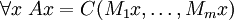
![\ Forall x \ B x = \ sqrt [p] {C (x_1 ^ p, \ dots, x_n ^ p)}](../../images/135/13518.png)
![\ Forall x \ B x = \ sqrt [p] {M_1 (x_1 ^ p, \ dots, x_n ^ p)}](../../images/135/13521.png)
