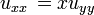Ecuación en derivadas parciales
Sabías ...
SOS Children, una organización benéfica educación , organizó esta selección. Visite el sitio web de Aldeas Infantiles SOS en http://www.soschildren.org/
En matemáticas , ecuaciones diferenciales parciales (PDE) son un tipo de ecuación diferencial , es decir, un relación que implica un desconocido función (o funciones) de varios variables independientes y su (resp.) su derivadas parciales con respecto a esas variables. Ecuaciones diferenciales parciales se utilizan para formular, y así ayudar a la solución de los problemas relacionados con las funciones de varias variables; tales como la propagación de sonido o de calor , electrostática, electrodinámica, flujo de fluido, elasticidad. Curiosamente, los fenómenos físicos aparentemente distintos pueden tener formulaciones matemáticas idénticas, y por lo tanto se rige por la misma dinámica subyacente.
Introducción
Una ecuación diferencial parcial es relativamente simple
Esta relación implica que los valores de u (x, y) son independientes de x. Por lo tanto el solución general de esta ecuación es
donde f es una función arbitraria (diferenciable) de y. El análogo ecuación diferencial ordinaria es
que tiene la solución
donde c es cualquier valor constante (independiente de x). Estos dos ejemplos ilustran que las soluciones generales de las ecuaciones diferenciales ordinarias implican constantes arbitrarias, pero las soluciones de las ecuaciones diferenciales parciales implican funciones arbitrarias. Una solución de una ecuación diferencial parcial no es generalmente único; condiciones adicionales se deben especificar en general sobre la límite de la región donde se define la solución. Por ejemplo, en el sencillo ejemplo anterior, la función  se puede determinar si
se puede determinar si  se especifica en la línea
se especifica en la línea  .
.
Existencia y unicidad
Aunque el tema de la existencia y unicidad de soluciones de ecuaciones diferenciales ordinarias tiene una respuesta muy satisfactoria con el Teorema de Picard-Lindelöf, que está lejos de ser el caso para las ecuaciones en derivadas parciales. Hay un teorema general (la Cauchy-Kovalevskaya teorema) que indica que el Problema de Cauchy para cualquier ecuación diferencial parcial que es analítica en la función desconocida y sus derivados tienen una solución analítica único. Aunque este resultado podría aparecer para liquidar la existencia y unicidad de soluciones, hay ejemplos de ecuaciones diferenciales parciales lineales cuyos coeficientes tienen derivadas de todos los órdenes (que sin embargo no son analíticas) pero que no tienen soluciones a todos: ver Lewy (1957). Incluso si existe la solución de una ecuación diferencial parcial y es único, puede sin embargo tener propiedades indeseables.
Un ejemplo de comportamiento patológico es la secuencia de problemas de Cauchy (dependiendo n) para el Ecuación de Laplace
con condiciones iniciales
donde n es un número entero. La derivada de u con respecto a y se aproxima a 0 uniformemente en x cuando n aumenta, pero la solución es
Esta solución tiende a infinito si nx no es un múltiplo entero de π para cualquier valor distinto de cero de y. El problema de Cauchy para la ecuación de Laplace se llama mal planteado o no bien planteado, ya que la solución no depende continuamente en los datos del problema. Tales problemas planteados malos no son generalmente satisfactorios para las aplicaciones físicas.
Notación y ejemplos
En PDEs, es común para denotar derivadas parciales utilizando subíndices. Esto es:
Especialmente en (matemática) la física, a menudo se prefiere el uso de del (que en coordenadas cartesianas se escribe  para derivadas espaciales y un punto
para derivadas espaciales y un punto 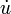 para los derivados de tiempo, por ejemplo, para escribir la ecuación de onda (ver abajo) como
para los derivados de tiempo, por ejemplo, para escribir la ecuación de onda (ver abajo) como
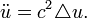 (Notación matemática)
(Notación matemática)
 (Notación física)
(Notación física)
Ecuación del calor en una dimensión espacio
La ecuación para la conducción del calor en una dimensión de un cuerpo homogéneo tiene la forma
donde u (t, x) es la temperatura, y α es una constante positiva que describe la velocidad de difusión. El problema de Cauchy para esta ecuación consiste en especificar  , Donde f (x) es una función arbitraria.
, Donde f (x) es una función arbitraria.
Soluciones generales de la ecuación del calor se pueden encontrar por el método de la separación de variables. Algunos ejemplos aparecen en el artículo ecuación del calor. Son ejemplos de Serie de Fourier para f periódico y Transformadas de Fourier de f no periódica. Usando la transformada de Fourier, una solución general de la ecuación de calor tiene la forma
donde F es una función arbitraria. Con el fin de satisfacer la condición inicial, F está dada por la transformada de Fourier de f, es decir
Si f representa una muy pequeña pero intensa fuente de calor, entonces la integral anterior se puede aproximar por la distribución delta, multiplicado por la fuerza de la fuente. Para una fuente cuya fuerza está normalizado a 1, el resultado es
y la solución resultante de la ecuación del calor es
Esto es un Gaussian integral. Se puede evaluar para obtener
Este resultado corresponde a una densidad de probabilidad normal para x con media 0 y varianza 2α t. La ecuación del calor y similares ecuaciones de difusión son herramientas útiles para el estudio de fenómenos aleatorios.
Ecuación de onda en una dimensión espacial
La ecuación de onda es una ecuación para una función desconocida u (t, x) de la forma
Aquí u podría describir el desplazamiento de una cadena estirada del equilibrio, o la diferencia en la presión de aire en un tubo, o la magnitud de un campo electromagnético en un tubo, y c es un número que corresponde a la velocidad de la onda. El problema de Cauchy para esta ecuación consiste en la prescripción el desplazamiento inicial y la velocidad de una cadena u otro medio de:
donde f y g son funciones dadas arbitrarias. La solución de este problema está dada por La fórmula de d'Alembert:
Esta fórmula implica que la solución a (t, x) sólo depende de los datos en el segmento de la línea inicial que se corta por la curvas características
que se sienten atraídos hacia atrás desde ese punto. Estas curvas corresponden a las señales que se propagan con la velocidad c hacia adelante y hacia atrás. Por el contrario, la influencia de los datos en cualquier punto dado en la línea inicial se propaga con la velocidad finita c: no hay ningún efecto fuera de un triángulo a través de ese punto de cuyos lados son curvas características. Este comportamiento es muy diferente de la solución para la ecuación del calor, donde el efecto de una aparece fuente puntual (con pequeña amplitud) instantáneamente en todos los puntos en el espacio. La solución dada anteriormente también es válido si t es negativo, y la fórmula explícita muestra que la solución depende sin problemas en los datos: tanto hacia adelante y hacia atrás problemas de Cauchy para la ecuación de onda son bien planteado.
Ondas esféricas
Ondas esféricas son ondas cuya amplitud depende sólo de la distancia radial r desde el centro de una fuente puntual. Para este tipo de olas, la ecuación de onda tridimensional toma la forma
Esto es equivalente a
y por lo tanto la cantidad ru satisface la ecuación de onda unidimensional. Por lo tanto una solución general para ondas esféricas tiene la forma
donde F y G son completamente funciones arbitrarias. La radiación de una antena corresponde al caso en que G es idénticamente cero. Así, la forma de onda transmitida desde una antena no tiene ninguna distorsión en el tiempo: el único factor de distorsión es de 1 / r. Esta característica de propagación sin distorsión de ondas no está presente si hay dos dimensiones espaciales.
Ecuación de Laplace en dos dimensiones
La Ecuación de Laplace de una función desconocida de dos variables φ tiene la forma
Las soluciones de la ecuación de Laplace se llaman funciones armónicas.
Conexión con funciones
Las soluciones de la ecuación de Laplace están íntimamente conectados con las funciones analíticas de una variable compleja (aka funciones holomorfas): las partes real e imaginaria de una función analítica son funciones armónicas conjugadas: ambos satisfacen la ecuación de Laplace, y sus gradientes son ortogonales. Si f = u + iv, entonces la Cauchy-Riemann ecuaciones de estado que
y se deduce que
Por el contrario, dado cualquier función armónica, es la parte real de una función analítica, al menos localmente. Los detalles se dan en Ecuación de Laplace.
Un problema típico valor límite
Un problema típico para la ecuación de Laplace es encontrar una solución que satisfaga valores arbitrarios en el límite de un dominio. Por ejemplo, podemos buscar una función armónica que adquiere los valores u (θ) en un círculo de radio uno. La solución fue dada por Poisson:
Petrovsky (1967, p. 248) muestra cómo esta fórmula se puede obtener sumando una serie de Fourier para φ. Si r <1, los derivados de φ se pueden calcular mediante la diferenciación bajo el signo integral, y uno puede verificar que φ es analítica, incluso si u es continua, pero no necesariamente diferenciable. Este comportamiento es típico para soluciones de ecuaciones diferenciales parciales elípticas: las soluciones pueden ser mucho más suave que los datos de contorno. Esto está en contraste con las soluciones de la ecuación de onda, y más general ecuaciones diferenciales parciales hiperbólicas, que normalmente no tienen más derivados que los datos.
Ecuación de Euler-Tricomi
La Ecuación de Euler-Tricomi se utiliza en la investigación de flujo transónico. Es
Ecuación de advección
La ecuación de advección describe el transporte de un escalar conservado  en un campo de velocidad
en un campo de velocidad  . Es:
. Es:
Si el campo de velocidad es solenoidal (es decir, 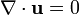 ), Entonces la ecuación se puede simplificar a
), Entonces la ecuación se puede simplificar a
La única ecuación de advección flujo constante dimensional 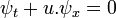 (Donde
(Donde  es constante) se conoce comúnmente como el problema chiquero. Si
es constante) se conoce comúnmente como el problema chiquero. Si  no es constante e igual a
no es constante e igual a  la ecuación se conoce como Ecuación de Burgers.
la ecuación se conoce como Ecuación de Burgers.
Ecuación de Ginzburg-Landau
La Ecuación de Ginzburg-Landau se utiliza en el modelado de la superconductividad . Es
donde 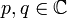 y
y  son constantes y
son constantes y  es la unidad imaginaria.
es la unidad imaginaria.
La ecuación de Dym
La Ecuación de Dym se nombra para Harry Dym y se produce en el estudio de solitones. Es
Otros ejemplos
La Ecuación de Schrödinger es un PDE en el corazón de no relativistas mecánica cuántica . En el Aproximación WKB es la Ecuación de Hamilton-Jacobi.
A excepción de la ecuación de Dym y la ecuación de Ginzburg-Landau, las anteriores ecuaciones son lineales en el sentido de que pueden ser escritos en forma Au = f para un determinado operador lineal A y la función f dada. Otras ecuaciones no lineales importantes incluyen las ecuaciones de Navier-Stokes que describen el flujo de fluidos, y la de Einstein ecuaciones de campo de la relatividad general .
Métodos para resolver PDEs
El método de la separación de variables rendirá soluciones particulares de un PDE linear en dominios muy simples, como rectángulos que puedan satisfacer las condiciones iniciales o de frontera. Debido a que cualquier superposición de soluciones de una PDE lineal es de nuevo una solución, las soluciones en particular, entonces se pueden combinar para obtener soluciones más generales. Si el dominio es finita o periódica, una suma infinita de soluciones, tales como una Serie de Fourier es apropiado, pero una integral de soluciones como una Integral de Fourier se requiere generalmente para dominios infinitos. La solución para una fuente puntual para la ecuación del calor dada anteriormente es un ejemplo para el uso de una integral de Fourier.
Problemas de valor inicial-frontera
Muchos de los problemas de la física matemática se formulan como problemas de valor inicial-fronterizos.
Cuerda vibrante
Si la cadena se estira entre dos puntos en los que x = 0 y x = L y U indica la amplitud del desplazamiento de la cadena, entonces u satisface la ecuación de onda unidimensional en la región donde 0 <x <L y t es ilimitado . Dado que la cadena está atado en los extremos, u también deberán cumplir las condiciones de contorno
así como las condiciones iniciales
El método de separación de variables para la ecuación de onda
conduce a soluciones de la forma
donde
donde la constante k debe ser determinado. Las condiciones de contorno a continuación, implica que X es un múltiplo de kx pecado, y k debe tener la forma
donde n es un número entero. Cada término en la suma corresponde a un modo de vibración de la cuerda. El modo con n = 1 se llama el modo fundamental, y las frecuencias de los otros modos son todas múltiplos de esta frecuencia. Ellos forman la Entonada serie de la cadena, y son la base para la acústica musical. Las condiciones iniciales pueden entonces ser satisfechos mediante la representación de f y g como infinitas sumas de estos modos. Instrumentos de viento típicamente corresponden a vibraciones de una columna de aire con un extremo abierto y un extremo cerrado. Las condiciones de contorno correspondientes son
El método de separación de variables también se puede aplicar en este caso, y conduce a una serie de armónicos impares.
El problema general de este tipo se resuelve en Teoría de Sturm-Liouville.
Membrana vibratoria
Si una membrana se estira sobre una curva C que forma el límite de un dominio D en el plano, sus vibraciones se rigen por la ecuación de onda
Si t> 0 y (x, y) está en D. La condición de frontera es  si
si 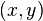 está en
está en  . El método de separación de variables conduce a la forma
. El método de separación de variables conduce a la forma
que a su vez deben satisfacer
La última ecuación se denomina Helmholtz ecuación. La constante k debe ser determinada con el fin de permitir una v no trivial para satisfacer la condición de frontera en C. Tales valores de k 2 se llaman los valores propios del Laplaciano en D, y las soluciones asociadas son las funciones propias del Laplaciano en D. La teoría de Sturm-Liouville se puede extender a este problema de valores propios elíptica (Jost, 2002).
No hay en general métodos aplicables para resolver PDEs no lineales. Sin embargo, la existencia y unicidad resultados (como el Cauchy-Kovalevskaya teorema) a menudo son posibles, como son las pruebas de importantes propiedades cualitativas y cuantitativas de las soluciones (obtener estos resultados es una parte importante del análisis ). Solución computacional a las PDEs no lineales, la Método Split-paso, existir para ecuaciones específicas como la ecuación no lineal de Schrödinger.
Sin embargo, algunas técnicas pueden utilizarse para varios tipos de ecuaciones. La h-principio es el método más poderoso para resolver ecuaciones indeterminados. La Teoría Riquier-Janet es un método eficaz para la obtención de información sobre muchos analítica sistemas sobredeterminados.
La método de las características ( Método de transformación de semejanza) se puede utilizar en algunos casos muy especiales para resolver ecuaciones diferenciales parciales.
En algunos casos, una PDE puede ser resuelto a través de análisis de perturbación en el que se considera que la solución sea una corrección a una ecuación con una solución conocida. Las alternativas son técnicas de análisis numérico de sencillo esquemas de diferencias finitas a los más maduros multigrid y métodos de elementos finitos. Muchos de los problemas de interés en la ciencia y la ingeniería se resuelven de esta forma el uso de las computadoras , a veces de alto rendimiento supercomputadoras.
Clasificación
Algunas ecuaciones diferenciales parciales, lineal de segundo orden pueden ser clasificados como parabólica, hiperbólica o elíptica. Otros, como el Ecuación de Euler-Tricomi tienen diferentes tipos de diferentes regiones. La clasificación proporciona una guía para apropiarse de las condiciones iniciales y de frontera, y la suavidad de las soluciones.
Ecuaciones de segundo orden
Suponiendo  , La EDP de segundo orden general de dos variables independientes tiene la forma
, La EDP de segundo orden general de dos variables independientes tiene la forma
donde los coeficientes A, B, C, etc. puede depender de x e y. Esta forma es análoga a la ecuación para una sección cónica:
Así como uno clasifica las secciones cónicas en parabólica, hiperbólica, elíptica y sobre la base de la discriminante 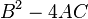 , El mismo se puede hacer para una EDP de segundo orden en un punto dado.
, El mismo se puede hacer para una EDP de segundo orden en un punto dado.
 : soluciones de PDEs elípticas son tan suaves como los coeficientes permiten, en el interior de la región donde se definen la ecuación y soluciones. Por ejemplo, las soluciones de la ecuación de Laplace son analíticas en el dominio en el que se definen, pero las soluciones pueden asumir valores límite que no son suaves. El movimiento de un fluido a velocidades subsónicas se puede aproximar con PDEs elípticas, y la ecuación de Euler-Tricomi es elíptica donde x <0.
: soluciones de PDEs elípticas son tan suaves como los coeficientes permiten, en el interior de la región donde se definen la ecuación y soluciones. Por ejemplo, las soluciones de la ecuación de Laplace son analíticas en el dominio en el que se definen, pero las soluciones pueden asumir valores límite que no son suaves. El movimiento de un fluido a velocidades subsónicas se puede aproximar con PDEs elípticas, y la ecuación de Euler-Tricomi es elíptica donde x <0.  ecuaciones que son: parabólica en cada punto puede ser transformado en una forma análoga a la ecuación del calor por un cambio de variables independientes. Soluciones suavizan como las variables transformadas tiempo aumenta. La ecuación de Euler-Tricomi tiene tipo parabólico en la línea donde x = 0.
ecuaciones que son: parabólica en cada punto puede ser transformado en una forma análoga a la ecuación del calor por un cambio de variables independientes. Soluciones suavizan como las variables transformadas tiempo aumenta. La ecuación de Euler-Tricomi tiene tipo parabólico en la línea donde x = 0. 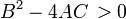 : ecuaciones hiperbólicas conservan cualquier discontinuidad de funciones o derivados en los datos iniciales. Un ejemplo es el ecuación de onda. El movimiento de un fluido a velocidades supersónicas se puede aproximar con PDEs hiperbólicas, y la ecuación de Euler-Tricomi es hiperbólica, donde x> 0.
: ecuaciones hiperbólicas conservan cualquier discontinuidad de funciones o derivados en los datos iniciales. Un ejemplo es el ecuación de onda. El movimiento de un fluido a velocidades supersónicas se puede aproximar con PDEs hiperbólicas, y la ecuación de Euler-Tricomi es hiperbólica, donde x> 0.
Si hay n variables independientes x 1, x 2, ..., x n, una ecuación diferencial parcial lineal general de segundo orden tiene la forma
La clasificación depende de la firma de los valores propios de la matriz de coeficientes.
- Elíptico: Los valores propios son positivos o negativos.
- Parabólico: Los valores propios son todos positivos o todos negativos, excepto una que es cero.
- Hiperbólica: Sólo hay un valor propio negativo y todo lo demás son positivos, o sólo hay un valor propio positivo y todo el resto son negativos.
- Ultrahyperbolic: No más de un valor propio positivo y más de un valor propio negativo, y no hay valores propios cero. Sólo hay teoría limitada para las ecuaciones ultrahyperbolic (Courant y Hilbert, 1962).
Sistemas de ecuaciones de primer orden y superficies características
La clasificación de las ecuaciones diferenciales parciales se puede extender a los sistemas de ecuaciones de primer orden, donde la u desconocido es ahora un vector con m componentes, y las matrices de coeficientes  son m por m matrices para
son m por m matrices para 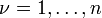 . La ecuación diferencial parcial toma la forma
. La ecuación diferencial parcial toma la forma
donde el coeficiente de matrices A ν y el vector B puede depender de x y u. Si una hipersuperficie S se da en la forma implícita
donde φ tiene un gradiente diferente de cero, entonces S es una superficie característica para el operador L en un punto dado, si la forma característica desaparece:
La interpretación geométrica de esta condición es la siguiente: si los datos de u se prescriben en la superficie S, entonces puede ser posible determinar la derivada normal de u en S de la ecuación diferencial. Si los datos de S y la ecuación diferencial determinan la derivada normal del u en el S, entonces S no es característica. Si los datos de S y la ecuación diferencial no determinan el derivado normal del u en S, entonces la superficie es característica, y la ecuación diferencial restringe los datos de S: la ecuación diferencial es interno a S.
- Un sistema de primer orden Lu = 0 es elíptica si hay superficie se caracteriza por L: los valores de u en S y la ecuación diferencial siempre determinan la derivada normal del u en el S.
- Un sistema de primer orden es hiperbólica en un punto si hay una superficie S-espacio como con ξ normales en ese punto. Esto significa que, dado cualquier η no trivial vector ortogonal a ξ, y un multiplicador escalar λ, la ecuación
m tiene raíces reales λ 1, λ 2, ..., λ m. El sistema es estrictamente hiperbólico si estas raíces son siempre distintas. La interpretación geométrica de esta condición es la siguiente: la forma Q característica (ζ) = 0 define un cono (el cono normal) con coordenadas homogéneas ζ. En el caso hiperbólico, este cono tiene hojas m, y el eje ζ = λ ξ se ejecuta dentro de estas hojas: que no se cruza con ninguna de ellas. Pero cuando se desplaza desde el origen por η, este eje se cruza cada hoja. En el caso elíptica, el cono normal, no tiene hojas reales.
Ecuaciones de tipo mixto
Si un PDE tiene coeficientes que no son constantes, es posible que no pertenece a ninguna de estas categorías, sino más bien ser de tipo mixto. Un ejemplo simple pero importante es la ecuación de Euler-Tricomi
que se llama elíptico-hiperbólica porque es elíptica en la región x <0, hiperbólica en la región x> 0, y parabólica degenerado en la línea x = 0.



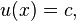




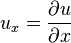



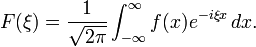
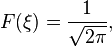


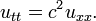

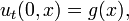
![u (t, x) = \ frac {1} {2} \ left [f (x-ct) + f (x + ct) \ right] + \ frac {1} {2c} \ int_ {x-ct} ^ {x + ct} g (y) \, dy. \,](../../images/89/8985.png)

![u_ {tt} = c ^ 2 \ left [u_ {rr} + \ frac {2} {r} U_r \ right]. \,](../../images/89/8987.png)
![(Ru) _ {tt} = c ^ 2 \ left [(ru) _ {rr} \ right], \,](../../images/89/8988.png)
![u (t, r) = \ frac {1} {r} \ left [F (r-ct) + G (r + ct) \ right], \,](../../images/89/8989.png)
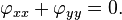


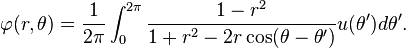
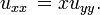



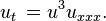


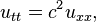
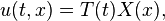

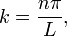
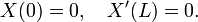
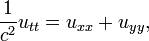

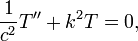


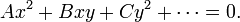



![Q \ se fue (\ frac {\ part \ phi} {\ x_1 parcial}, \ ldots, \ frac {\ part \ phi} {\ x_n parcial} \ right) = \ det \ left [\ sum _ {\ nu = 1 } ^ Na + \ nu \ frac {\ partial \ phi} {\ x_ parcial \ nu} \ right] = 0 \.,](../../images/90/9030.png)