Función de Bessel

Temas relacionados: Matemáticas

Sabías ...

Esta selección Escuelas fue originalmente elegido por SOS para las escuelas en el mundo en desarrollo que no tienen acceso a Internet. Está disponible como una descarga intranet. Visite el sitio web de Aldeas Infantiles SOS en http://www.soschildren.org/

En matemáticas , las funciones de Bessel, primero definidas por el matemático Daniel Bernoulli y generalizada por Friedrich Bessel, son soluciones canónica y (x) de Bessel de ecuación diferencial :

$x ^ 2 \ frac {d ^ 2 y} {dx ^ 2} + x \ frac {dy} {dx} + (x ^ 2 - \ alpha ^ 2) y = 0$

para un número arbitrario α real o complejo. El caso especial más común e importante es donde α es un número entero n, entonces α se conoce como el orden de la función de Bessel.

Aunque α y -α producir la misma ecuación diferencial, es convencional para definir diferentes funciones de Bessel para estos dos órdenes (por ejemplo, de modo que las funciones de Bessel son en su mayoría funciones suaves de α). Funciones de Bessel también se conocen como funciones de cilindro o armónicos cilíndricos porque se encuentran en la solución de La ecuación de Laplace en coordenadas cilíndricas.

Aplicaciones

La ecuación de Bessel se presenta cuando la búsqueda de soluciones a separables Y la ecuación de Laplace Ecuación de Helmholtz en cilíndrica o coordenadas esféricas . Por lo tanto, las funciones de Bessel son especialmente importantes para muchos problemas de la propagación de ondas, los potenciales estáticos, y así sucesivamente. En la resolución de problemas en los sistemas de coordenadas cilíndrico, se obtienen las funciones de Bessel de orden entero (α = n); en problemas esféricas, se obtiene órdenes media enteros (α = n + ½). Por ejemplo:

las ondas electromagnéticas en un cilíndrico guía de onda
la conducción de calor en un objeto cilíndrico.
modos de vibración de una circular delgada (o anular) membrana artificial.
problemas de difusión en una red.

Funciones de Bessel también tienen propiedades útiles para otros problemas, tales como el procesamiento de señales (por ejemplo, véase Síntesis FM, Ventana de Kaiser, o Filtro de Bessel).

Definiciones

Como se trata de una ecuación diferencial de segundo orden, tiene que haber dos soluciones linealmente independientes. Dependiendo de las circunstancias, sin embargo, varias formulaciones de estas soluciones son convenientes, y las diferentes variaciones se describen a continuación.

Funciones de Bessel de primera clase: $J_ \ alpha$

Funciones de Bessel de primera especie, denominado J _α (x), son soluciones de la ecuación diferencial de Bessel que son finitos en el origen (x = 0) para α enteros no negativos, y divergen cuando x tiende a cero para no entero negativo α. El tipo de solución (por ejemplo, entero o no entero) y la normalización de J _α (x) se definen por sus propiedades de abajo. Para las soluciones de orden enteros, es posible definir la función por su serie de Taylor alrededor de expansión x = 0:

$J_ \ alpha (x) = \ sum_ {m = 0} ^ \ infty \ frac {(- 1) ^ m} {m! \ Gamma (m + \ alpha + 1)} {\ left ({\ frac {x} {2}} \ right)} ^ {2m + \ alpha}$

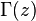donde $\ Gamma (z)$ es el función gamma, una generalización del factorial función a los valores no enteros. Para no entero α, una más general serie de potencias se requiere la expansión. Las gráficas de las funciones de Bessel se ven más o menos como oscilante funciones seno o coseno que decaen de forma proporcional a 1 / √ x (ver también sus formas asintóticas abajo), aunque sus raíces no son generalmente periódica, excepto asintóticamente para grandes x. (La serie de Taylor indica que $-J_1 (X)$ es la derivada de $J_0 (x)$ , Al igual $- \ Sin$ es la derivada de $\ cos$ ; más en general, el derivado de $J_n (x)$ se puede expresar en términos de $J_ {n \ pm 1} (x)$ por las identidades de abajo ).

Parcela de la función de Bessel de primera especie, J _α (x), para las órdenes enteros α = 0,1,2.

Para α no enteros, las funciones $J_ \ alpha (x)$ y $J _ {- \ alpha} (x)$ son linealmente independientes, y por lo tanto son las dos soluciones de la ecuación diferencial. Por otro lado, para la orden de número entero $\ Alpha$ , La siguiente relación es válida:

$J _. {- N} (x) = (-1) ^ n J_ {n} (x) \,$

Esto significa que las dos soluciones ya no son linealmente independientes. En este caso, la segunda solución linealmente independiente se encuentra a continuación, a ser la función de Bessel de segundo tipo, como se discute a continuación.

Integrales de Bessel

Otra definición de la función de Bessel, para valores enteros de $n$ , Es posible utilizando una representación integral:

$J_n (x) = \ frac {1} {\ pi} \ int_ {0} ^ {\ pi} \ cos (n \ tau - x \ sin \ tau) d \ tau.$

Este fue el enfoque que Bessel utilizado, y de esta definición se deriva varias propiedades de la función.

Otra representación integral es:

$J_n (x) = frac {1} {2 \ pi} \ int _ \ {- \ pi} ^ {\ pi} e ^ {- i (n \ tau - x \ sin \ tau)} d \ tau$

Relación con la serie hipergeométrica

Las funciones de Bessel se pueden expresar en términos de la serie hipergeométrica como

$J_ \ alpha (z) = \ frac {(z / 2) ^ \ alpha} {\ Gamma (\ alpha + 1)} \; _ 0F_1 (\ alpha + 1; z ^ 2/4).$

Esta expresión está relacionada con el desarrollo de las funciones de Bessel en términos de la Función de Bessel-Clifford.

Funciones de Bessel de segunda clase: $Y_ \ alpha$

Las funciones de Bessel de segunda especie, indicados por Y _α (x), son soluciones de la ecuación diferencial de Bessel. Son singulares ( infinita) en el origen (x = 0).

Parcela de la función de Bessel de segunda especie, Y _α (x), para las órdenes enteros α = 0,1,2.

_Α y (x) veces también se llama la función de Neumann, y de vez en cuando se denota no por N _α (x). Para no enteros α, que está relacionado con J _α (x) por:

$Y_ \ alpha (x) = \ frac {J_ \ alpha (x) \ cos (\ alpha \ pi) - J _ {- \ alpha} (x)} {\ sin (\ alpha \ pi)}.$

En el caso de orden entero n, la función se define tomando el límite como no entero α tiende a n ':

$Y_n (x) = \ lim _ {\ alpha \ an} Y_ \ alpha (x),$

que tiene el resultado (en forma integral)

$Y_n (x) = \ frac {1} {\ pi} \ int_ {0} ^ {\ pi} \ sin (x \ sin \ theta - n \ theta) d \ theta - \ frac {1} {\ pi} \ int_ {0} ^ {\ infty} \ left [e ^ {nt} + (-1) ^ ne ^ {- nt} \ right] e ^ {- x \ senh t} dt.$

Para el caso de no enteros α, la definición de Y _α (x) es redundante (como se desprende de su definición anterior). Por otra parte, cuando α es un número entero, Y _α (x) es la segunda solución linealmente independientes de la ecuación de Bessel; Por otra parte, como era de manera similar en el caso de las funciones de la primera clase, la siguiente relación es válida:

$Y _. {- N} (x) = (-1) ^ n y_n (x) \,$

Ambos J _α (x) e Y _α (x) son funciones holomorfas de x en el plano complejo cortan a lo largo del eje real negativo. Cuando α es un número entero, no hay punto de ramificación, y las funciones de Bessel son funciones enteras de x. Si x se mantiene fijo, entonces las funciones de Bessel son funciones enteras de α.

Funciones de Hankel: $H_ \ alpha$

Otra formulación importante de las dos soluciones linealmente independientes de la ecuación de Bessel son la Hankel funciones H _α ⁽¹⁾ (x) y H _α ⁽²⁾ (x), definida por:

$H_ \ alpha ^ {(1)} (x) = J_ \ alpha (x) + i Y_ \ alpha (x)$

$H_ \ alpha ^ {(2)} (x) = J_ \ alpha (x) - i Y_ \ alpha (x)$

donde i es la unidad imaginaria . Estas combinaciones lineales también se conocen como funciones de Bessel de tercera clase; son dos soluciones linealmente independientes de la ecuación diferencial de Bessel. Las funciones de Hankel de primera y segunda clase se utilizan para expresar hacia el exterior y hacia el interior de propagación de soluciones de onda cilíndrica de la ecuación de onda cilíndrica, respectivamente (o viceversa, dependiendo de la convención de signos para el frecuencia). Se nombran después Hermann Hankel.

Usando las relaciones anteriores se pueden expresar como:

$H _ {\ alpha} ^ {(1)} (x) = \ frac {J _ {- \ alpha} (x) - e ^ {- \ alpha \ pi i} J_ \ alpha (x)} {i \ sin ( \ alpha \ pi)}$

$H _ {\ alpha} ^ {(2)} (x) = \ frac {J _ {- \ alpha} (x) - e ^ {\ alpha \ pi i} J_ \ alpha (x)} {- i \ sin ( \ alpha \ pi)}$

Si α es un número entero, el límite tiene que ser calculado. Las siguientes relaciones son válidas, si α es un entero o no:

$H _ {- \ alpha} ^ {(1)} (x) = e ^ {\ alpha \ pi i} H _ {\ alpha} ^ {(1)} (x)$

$H _ {- \ alpha} ^ {(2)} (x) = e ^ {- \ alpha \ pi i} H _ {\ alpha} ^ {(2)} (x)$

Funciones de Bessel modificadas: $I_ \ alpha, K_ \ alpha$

Las funciones de Bessel son válidos incluso para complejos argumentos x, y un importante caso especial es el de un argumento puramente imaginario. En este caso, las soluciones a la ecuación de Bessel se llaman las funciones de Bessel modificadas (u ocasionalmente las funciones hiperbólicas de Bessel) de la primera y segunda clase, y se definen por:

$I_ \ alpha (x) = i ^ {- \ alpha} J_ \ alpha (ix) \!$

$K_ \ alpha (x) = \ frac {\ pi} {2} \ frac {I _ {- \ alpha} (x) - I_ \ alpha (x)} {\ sin (\ alpha \ pi)} = \ frac { \ pi} {2} i ^ {\ alpha + 1} H_ \ alpha ^ {(1)} (ix) \!$

Estos son elegidos para ser para argumentos reales x de valor real. La expansión de la serie de I _α (x) es por lo tanto similar a la de _α J (x), pero sin la alterna (-1) factor de ^m.

I _α (x) y K _α (x) son las dos soluciones linealmente independientes de la ecuación de Bessel modificada:

$x ^ 2 \ frac {d ^ 2 y} {dx ^ 2} + x \ frac {dy} {dx} - (x ^ 2 + \ alpha ^ 2) y = 0.$

A diferencia de las funciones ordinarias de Bessel, que son oscilante como funciones de un argumento real, _α y K _α están creciendo exponencialmente y descomposición funciones, respectivamente. Al igual que el ordinario la función de Bessel J _α, la función de I _α tiende a cero en x = 0 para α> 0 y es finita en x = 0 para α = 0. Análogamente, K _α diverge en x = 0.

Funciones de Bessel modificadas de primera clase, me _α (x), para α = 0,1,2,3

Funciones de Bessel modificadas de segunda clase, K _α (x), para α = 0,1,2,3

La función de Bessel modificada de la segunda clase también ha sido llamado por los nombres ahora raras:

Función Basset
función de Bessel modificada del tercer tipo
Función MacDonald

Esféricos funciones de Bessel: $j_n, y_n$

Funciones esféricas de Bessel de primera clase, j _n (x), para n = 0,1,2

Funciones de Bessel esféricas de segunda clase, y _n (x), para n = 0,1,2

Al resolver el Ecuación de Helmholtz en coordenadas esféricas por separación de variables, la ecuación radial tiene la forma:

$x ^ 2 \ frac {d ^ 2 y} {dx ^ 2 + 2x} \ frac {dy} {dx} + [x ^ 2 - n (n + 1)] y = 0.$

Las dos soluciones linealmente independientes de esta ecuación se llaman esférica Bessel funciona j _n e y _n, y están relacionados con la ordinaria Bessel J funciones _n e Y _n por:

$j_n (x) = \ sqrt {\ frac {\ pi} {2x}} J_ {n + 1/2} (x),$

$y_n (x) = \ sqrt {\ frac {\ pi} {2x}} Y_ {n + 1/2} (x) = (-1) ^ {n + 1} \ sqrt {\ frac {\ pi} { 2x}} J _ {- n-1/2} (x).$

$y_n$ También se denota $n_n$ o η _n; algunos autores llaman a estas funciones las funciones esféricas Neumann.

Las funciones de Bessel esféricas también pueden escribirse como:

$j_n (x) = (-x) ^ n \ left (\ frac {1} {x} \ frac {d} {dx} \ right) ^ n \, \ frac {\ sin x} {x},$

$y_n (x) = - (- x) ^ n \ left (\ frac {1} {x} \ frac {d} {dx} \ right) ^ n \, \ frac {\ cos x} {x}.$

La primera función de Bessel esférica $j_0 (x)$ También se conoce como el (unnormalized) función sinc. Las primeras funciones esféricas de Bessel son:

$j_0 (x) = \ frac {\ sin x} {x}$

$j_1 (x) = \ frac {\ sin x} {x ^ 2} - \ frac {\ cos x} {x}$

$J_2 (x) = \ left (\ frac {3} {x ^ 2} - 1 \ right) \ frac {\ sin x} {x} - \ frac {3 \ cos x} {x ^ 2}$

$y_0 (x) = - j _ {- 1} (x) = - \, \ frac {\ cos x} {x}$

$y_1 (x) = j _ {- 2} (x) = - \, \ frac {\ cos x} {x ^ 2} - \ frac {\ sin x} {x}$

$y_2 (x) = - j _ {- 3} (x) = \ left (- \, \ frac {3} {x ^ 2} 1 \ right) \ frac {\ cos x} {x} - \ frac { 3 \ sin x} {x ^ 2}.$

También son análogos esféricas de las funciones de Hankel:

$h_n ^ {(1)} (x) = j_n (x) + i y_n (x)$

$h_n ^ {(2)} (x) = j_n (x) - i y_n (x).$

De hecho, no son simples expresiones de forma cerrada para las funciones de Bessel de orden de medio entero en términos de los estándares funciones trigonométricas , y por lo tanto para las funciones esféricas de Bessel. En particular, para los números enteros no negativos N:

$h_n ^ {(1)} (x) = (-i) ^ {n + 1} \ frac {e ^ {ix}} {x} \ sum_ {m = 0} ^ n \ frac {i ^ m} { m! (2x) ^ m} \ frac {(n + m)!} {(nm)!}$

y h _n ⁽²⁾ es el complejo conjugado de este (por real x). De ello se deduce, por ejemplo, que j ₀ (x) = sin (x) / x e y ₀ (x) = -cos (x) / x, y así sucesivamente.

Funciones Riccati-Bessel: $S_n, C_n, \ zeta_n$

Funciones Riccati-Bessel sólo difieren ligeramente de las funciones esféricas de Bessel:

$S_n (x) = x j_n (x) = \ sqrt {\ pi x / 2} J_ {n + 1/2} (x)$

$C_n (x) = - x y_n (x) = - \ sqrt {\ pi x / 2} Y_ {n + 1/2} (x)$

$\ Zeta_n (x) = x ^ {h_n (2)} (x) = \ sqrt {\ pi x / 2} H_ {n + 1/2} ^ {(2)} (x) = S_n (x) + iC_n (x)$

Satisfacen la ecuación diferencial:

$x ^ 2 \ frac {d ^ 2 y} {dx ^ 2} + [x ^ 2 - n (n + 1)] y = 0$

Esta ecuación diferencial, y las soluciones Riccati-Bessel, surge en el problema de la dispersión de las ondas electromagnéticas por una esfera, conocido como La dispersión de Mie después de la primera solución publicada por Mie (1908). Véase, por ejemplo Du (2004) para la evolución reciente y las referencias.

Siguiente Debye (1909), la notación $\ Psi_n, \ chi_n$ se utiliza a veces en lugar de $S_n, C_n$ .

Formas asintóticas

Las funciones de Bessel tienen el siguiente formas asintóticas para α no negativo. Para los pequeños argumentos $0 <x \ ll \ sqrt {\ alpha + 1}$ , Se obtiene:

$J_ \ alpha (x) \ rightarrow \ frac {1} {\ Gamma (\ alpha + 1)} \ left (\ frac {x} {2} \ right) ^ \ alpha$

$Y_ \ alpha (x) \ rightarrow \ left \ {\ begin {matriz} \ frac {2} {\ pi} \ left [\ ln (x / 2) + \ gamma \ right] y \ mbox {si} \ alpha = 0 \\ \\ - \ frac {\ Gamma (\ alpha)} {\ pi} \ left (\ frac {2} {x} \ right) ^ \ alpha y \ mbox {si} \ alpha> 0 \ end {matriz} \ right.$

donde γ es el Euler-Mascheroni constante (0,5772 ...) y Γ puntos marca el la función gamma. Para grandes argumentos $x \ gg | \ alpha ^ 2 - 1/4 |$ , Se convierten:

$J_ \ alpha (x) \ rightarrow \ sqrt {\ frac {2} {\ pi x}} \ cos \ left (x \ frac {\ alpha \ pi} {2} - \ frac {\ pi} {4} \ right)$

$Y_ \ alpha (x) \ rightarrow \ sqrt {\ frac {2} {\ pi x}} \ sin \ left (x \ frac {\ alpha \ pi} {2} - \ frac {\ pi} {4} \ right).$

(Para α = 1/2 estas fórmulas son exactas; ver las funciones de Bessel esféricas anteriormente.) Formas asintótica para los otros tipos de función de Bessel siguen directa a partir de las relaciones anteriores. Por ejemplo, para la gran $x \ gg | \ alpha ^ 2 - 1/4 |$ , Las funciones de Bessel modificadas se convierten en:

$I_ \ alpha (x) \ rightarrow \ frac {1} {\ sqrt {2 \ pi x}} e ^ x,$

$K_ \ alpha (x) \ rightarrow \ sqrt {\ frac {\ pi} {2x}} e ^ {- x}.$

mientras que para pequeños argumentos $0 <x \ ll \ sqrt {\ alpha + 1}$ , Se convierten:

$I_ \ alpha (x) \ rightarrow \ frac {1} {\ Gamma (\ alpha + 1)} \ left (\ frac {x} {2} \ right) ^ \ alpha$

$K_ \ alpha (x) \ rightarrow \ left \ {\ begin {matriz} - \ ln (x / 2) - \ gamma y \ mbox {si} \ alpha = 0 \\ \\ \ frac {\ Gamma (\ alpha )} {2} \ left (\ frac {2} {x} \ right) ^ \ alpha y \ mbox {si} \ alpha> 0 \ end {matriz} \ right.$

Propiedades

Por orden entero α = n, J _n se define a menudo a través de un Desarrollo de Laurent de una función generadora:

$e ^ {(x / 2) (t-1 / t)} = \ sum_ {n = - \ infty} ^ \ infty j_n (x) t ^ n,$

un enfoque utilizado por PA Hansen en 1843. (Esto se puede generalizar a la orden no entero por la integración de contorno u otros métodos.) Otra relación importante para órdenes enteros es el Jacobi-Anger identidad:

$e ^ {iz \ cos \ phi} = \ sum_ {n = - \ infty} ^ \ infty i ^ n j_n (z) e ^ {en \ phi},$

que se utiliza para expandir una onda plana como una suma de ondas cilíndricas, o para encontrar la Serie de Fourier de un tono modulado Señal de FM.

Las funciones _α j, y _{α, α} H ^(1), y H _α ⁽²⁾ todos satisfacen la relaciones de recurrencia:

$Z _ {\ alpha-1} (x) + Z _ {\ alpha + 1} (x) = \ frac {2 \ alpha} {x} Z_ \ alpha (x)$

$Z _ {\ alpha-1} (x) - Z _ {\ alpha + 1} (x) = 2 \ frac {dZ_ \ alpha} {dx}$

donde Z designa J, Y, H ^(1), o H ^(2). (Estos dos identidades se combinan a menudo, por ejemplo, suma o se resta, para dar varias otras relaciones.) De esta manera, por ejemplo, se puede calcular funciones de Bessel de órdenes superiores (o sus derivados superiores) dados los valores en órdenes inferiores (o derivados inferiores ). En particular, se deduce que:

$\ Left (\ frac {d} {x dx} \ right) ^ m \ left [x ^ \ alpha Z _ {\ alpha} (x) \ right] = x ^ {\ alpha - m} Z _ {\ alpha - m } (x)$

$\ Left (\ frac {d} {x dx} \ right) ^ m \ left [\ frac {Z_ \ alpha (x)} {x ^ \ alpha} \ right] = (-1) ^ m \ frac {Z_ {\ alpha + m} (x)} {x ^ {\ alpha + m}}$

Funciones de Bessel modificadas siguen relaciones similares:

$e ^ {(x / 2) (t + 1 / t)} = \ sum_ {n = - \ infty} ^ \ infty I_N (x) t ^ n,$

$e ^ {z \ cos \ theta} = I_0 (z) + 2 \ sum_ {n = 1} ^ \ infty i_n (z) \ cos (n \ theta),$

La relación de recurrencia lee

$C _ {\ alpha-1} (x) - C _ {\ alpha + 1} (x) = \ frac {2 \ alpha} {x} C_ \ alpha (x)$

$C _ {\ alpha-1} (x) + C _ {\ alpha + 1} (x) = 2 \ frac {DC_ alpha \} {dx}$

donde C _α denota I _α o correo ^{απ i} K _α. Estas relaciones de recurrencia son útiles para los problemas de difusión discretos.

Debido a que la ecuación de Bessel se convierte Hermítica (autoadjunto) si se divide por x, las soluciones debe satisfacer una relación de ortogonalidad para las condiciones de contorno adecuadas. En particular, se deduce que:

$\ Int_0 ^ 1 x J_ \ alpha (x U _ {\ alpha, m}) J_ \ alpha (x U _ {\ alpha, n}) dx = \ frac {\ delta_ {m, n}} {2} [J_ { \ alpha + 1} (u _ {\ alpha, m})] ^ 2 = \ frac {\ delta_ {m, n}} {2} [J _ {\ alpha} '(u _ {\ alpha, m})] ^ 2,$

donde α> -1, δ _{m, n} es el Delta de Kronecker, yu _{α, m} es el m-ésimo cero de J _α (x). Esta relación de ortogonalidad puede entonces ser utilizado para extraer los coeficientes en la Serie de Fourier-Bessel, donde una función se expande en la base de las funciones J _{α (α} x _{u, m)} para α fijo y variando m. (Una relación análoga para las funciones esféricas de Bessel sigue inmediatamente.)

Otra relación de ortogonalidad es la ecuación de cierre:

$\ Int_0 ^ \ infty x J_ \ alpha (UX) J_ \ alpha (vx) dx = \ frac {1} {u} \ delta (u - v)$

para α> -1/2 y donde δ es el Función delta de Dirac. Esta propiedad se utiliza para construir una función arbitraria de una serie de funciones de Bessel por medio de la Transformada de Hankel. Para las funciones esféricas de Bessel la relación de ortogonalidad es:

$\ Int_0 ^ \ infty x ^ 2 j_ \ alpha (UX) j_ \ alpha (vx) dx = \ frac {\ pi} {2u ^ 2} \ delta (u - v)$

para α> 0.

Otra propiedad importante de las ecuaciones de Bessel, que se sigue de La identidad de Abel, implica la Wronskiano de las soluciones:

$A_ \ alpha (x) \ frac {db_ \ alpha} {dx} - \ frac {dA_ \ alpha} {dx} B_ \ alpha (x) = \ frac {C_ \ alpha} {x},$

donde A y B _{α α} son dos soluciones de la ecuación de Bessel, y C _α es una constante independiente de x (que depende de α y en las funciones de Bessel particulares considerados). Por ejemplo, si A = J _{α α} y B _{α α} = Y, a continuación, C _α es 2 / π. Esto también es válido para las funciones de Bessel modificadas; Por ejemplo, si A = I _{α α} y B _{α α} = k, entonces C _α es -1.

(Hay un gran número de otras integrales e identidades conocidas que no se reproducen aquí, pero que se pueden encontrar en las referencias.)

Teorema de multiplicación

Las funciones de Bessel obedecen a un teorema de la multiplicación

$\ Lambda ^ {- \ nu} J_ \ nu (\ lambda z) = \ sum_ {n = 0} ^ \ infty \ frac {1} {! N} \ left (\ frac {(1- \ lambda ^ 2) z} {2} \ right) ^ n J _ {\ nu + n} (z)$

donde $\ Lambda$ y $\ Nu$ puede tomarse como números complejos arbitrarios. Una forma similar se puede dar por $Y_ \ nu (z)$ y etc. Ver

Recuperado de " http://en.wikipedia.org/w/index.php?title=Bessel_function&oldid=207920326 "

See also ebooksgratis.com: no banners, no cookies, totally FREE.