Sistema de numeración

Temas relacionados: Matemáticas

Antecedentes

Este contenido de Wikipedia ha sido seleccionada por SOS para su utilización en las escuelas de todo el mundo. Infantil SOS es la mayor donación de caridad del mundo niños huérfanos y abandonados de la oportunidad de la vida familiar.

Sistemas de numeración por la cultura
Numerales indo-arábigos Western árabe Oriental Árabe Familia india Tamil Telugu Birmano Khmer Lao Mongol Tailandés Números de Asia Oriental Chino Japonés Suzhou Coreano Vietnamita Numeración con varillas Numerales alfabéticos Abjad Armenio Aryabhata Cirílico Ge'ez Griego Georgiano Hebreo Otros sistemas históricos Egeo Ático Babilónico Brahmi Egipcio Etrusco Inuit Kharosthi Maya Quipu Romano
Sistemas posicionales por base
Decimal (10)
1 2 3 4 5 6 7 8 9 11 12 13 14 15 16 20 24 26 27 32 36 60 64 85
Ternario Balanced
Lista de sistemas de numeración

Un sistema de numeración (o sistema de numeración) es una notación matemática para representar los números de un conjunto dado de símbolos de una manera consistente. Se puede observar como el contexto que permite que el numeral "11" para ser interpretada como la binaria numeral de tres, el decimal numeral de once, u otros números en diferentes bases.

Idealmente, un sistema de numeración hará lo siguiente:

Representar un útil conjunto de números (por ejemplo, todos los números enteros, enteros o números reales )
Dar a cada número representado una representación única (o al menos una representación de serie)
Reflejar la estructura algebraica y aritmética de los números.

Por ejemplo, el habitual decimal representación de números enteros da a cada número entero una representación única como una finito secuencia de dígitos , con las operaciones de la aritmética (suma, resta, multiplicación y división) están presentes como el estándar algoritmos de la aritmética. Sin embargo, cuando se utiliza la representación decimal de los racionales números o reales, la representación ya no es único: muchos números racionales tienen dos números, uno estándar que termina, tales como 2.31, y otros que se repite, como 2,309999999 .... Los números que terminan no tienen dígitos distintos de cero después de una posición dada. Por ejemplo, los mismos números 2.31 y 2.310 son llevados a ser el mismo, excepto en las ciencias experimentales, donde la mayor precisión se denota por el cero final.

Sistemas de numeración se denominan a veces los sistemas de numeración , pero ese nombre es engañoso, ya que podría hacer referencia a diferentes sistemas de números, tales como el sistema de los números reales , el sistema de los números complejos , el sistema de p números -adic, etc. Estos sistemas no son el tema de este artículo.

Tipos de sistemas de numeración

El sistema más comúnmente utilizado de números es conocido como Numerales indo-arábigos, y dos grandes matemáticos indios podrían dar crédito para el desarrollo de ellos. Aryabhatta de Kusumapura que vivió durante el siglo quinto desarrolló la notación de valor y lugar Brahmagupta un siglo más tarde introdujo el símbolo cero.

El sistema de numeración más simple es el sistema de numeración unario, en el que cada número natural está representada por un número correspondiente de símbolos. Si se elige el símbolo /, por ejemplo, entonces el número siete estaría representada por ///////. Marcas de conteo representan uno de estos sistemas todavía en uso común. En la práctica, el sistema unario es normalmente sólo es útil para pequeñas cantidades, a pesar de que juega un papel importante en la informática teórica. También, Elias codificación gamma que se utiliza comúnmente en la compresión de datos expresa números arbitrarios de tamaño mediante el uso de unario para indicar la longitud de un número binario.

La notación unaria puede abreviarse mediante la introducción de símbolos diferentes para ciertos valores nuevos. Muy comúnmente, estos valores son potencias de 10; Así, por ejemplo, si / representa uno, - para diez y + 100 para, a continuación, el número 304 se puede representar de forma compacta como +++ //// y el número 123 como + - - /// sin necesidad de cero. Se llama firmar valor notación. La antigua Sistema egipcio es de este tipo, y el sistema romano es una modificación de esta idea.

Más útil aún son sistemas que emplean abreviaturas especiales para repeticiones de símbolos; por ejemplo, el uso de los primeros nueve letras de nuestro alfabeto para estas abreviaturas, con un pie de "una ocurrencia", B "dos ocurrencias", y así sucesivamente, podríamos escribir C + D / para el número 304. El sistema de numeración de Inglés es de este tipo ("trescientos [y] cuatro"), como son las de prácticamente todos los demás habladas lenguas , independientemente de lo que los sistemas por escrito que han adoptado.

Más elegante es una sistema posicional, también conocida como la notación de valor posicional. Una vez que trabaja en base 10, utilizamos diez dígitos diferentes 0, ..., 9 y utilizar la posición de un dígito para significar la potencia de diez que el dígito es que ser multiplicado con, como en 304 = 3 × 100 + 0 × 10 + 4 × 1. Tenga en cuenta que cero , lo que no se necesita en los otros sistemas, es de crucial importancia aquí, con el fin de ser capaz de "saltar" una potencia. La Sistema de numeración hindú-árabe, tomado de la India , es un sistema de base 10 posicional; se utiliza hoy en día en todo el mundo.

La aritmética es mucho más fácil en sistemas posicionales que en los aditivos anteriores; Además, los sistemas de aditivos tienen una necesidad de un número potencialmente infinito de diferentes símbolos de las diferentes potencias de 10; sistemas posicionales sólo necesitan 10 símbolos diferentes (suponiendo que utiliza base 10).

Los números usados al escribir números con dígitos o símbolos se pueden dividir en dos tipos que podrían llamarse la números aritméticas y el 0,1,2,3,4,5,6,7,8,9 números geométricas 1,10,100,1000,10000 ... respectivamente. Los sistemas de registro de valor utilizan sólo los números geométricas y el sistema posicional utilizan sólo los números aritméticos. El sistema de registro de valor no necesita números aritméticos porque están hechos por la repetición (a excepción de la Sistema iónico), y el sistema de posición no necesita números geométricas porque están hechos por la posición. Sin embargo, la lengua hablada utiliza tanto la aritmética y los números geométricos.

En ciertas áreas de la informática, se utiliza un sistema posicional k basal modificado, llamado numeración biyectiva, con los dígitos 1, 2, ..., k (k ≥ 1), y cero está representado por la cadena vacía. Esto establece una biyección entre el conjunto de todas esas cuerdas dígitos y el conjunto de los enteros no negativos, evitando la no unicidad causada por ceros a la izquierda. Bijective basal k numeración también se llama notación -adic k, que no debe confundirse con números p-adic. Base 1 biyectiva el mismo que unario.

Bases utilizadas

En informática

Interruptores, imitado por sus sucesores electrónicos construidos originalmente de tubos de vacío y en la tecnología moderna de transistores, sólo tienen dos estados posibles: "abierto" y "cerrado". Sustituyendo abierto = 1 y cerrada = 0 (o al revés) produce todo el conjunto de dígitos binarios. Este sistema de base 2 ( binario ) es la base para computadoras digitales. Se utiliza para llevar a cabo la aritmética de enteros en casi todos los ordenadores digitales; alguna base-3 exótica ( ternarios) y la base-10 computadoras también se han construido, pero esos diseños fueron descartados temprano en la historia del hardware de computación .

Modernos ordenadores utilizan transistores que representan dos estados con voltajes altos o bajos. La unidad más pequeña de memoria para este estado binario se llama un poco. Los bits se organizan en grupos para ayudar en el proceso, y para que los números binarios más corto y más manejable para los seres humanos. Más recientemente, estos grupos de bits, tales como bytes y palabras, se dimensionan en múltiplos de cuatro. Por lo tanto la base 16 ( hexadecimal ) se utiliza comúnmente como taquigrafía. Base 8 (octal) también se ha utilizado para este propósito.

Una computadora no trata a todos sus datos como numérico. Por ejemplo, algunas de ellas pueden ser tratadas como instrucciones de programa o datos tales como texto. Sin embargo, la aritmética y la lógica booleana constituyen operaciones más internos. Los números enteros se representan exactamente, como enteros. Los números reales , permitiendo valores fraccionarios, por lo general se aproximan como Los números de coma flotante. El equipo utiliza diferentes métodos para hacer aritmética con estos dos tipos de números.

Cinco

Un sistema de base 5 ( quinario) se ha utilizado en muchas culturas para contar. Es evidente que se basa en el número de dedos en una mano humana. También puede considerarse como una sub-base de otras bases, tales como la base 10 y la base 60.

Ocho

Un sistema de base-8 ( octal) fue ideado por el Yuki del norte de California, que utiliza los espacios entre los dedos para contar. De cero a siete son los únicos dígitos posibles. También hay evidencia lingüística que sugiere que la Edad de Bronce Proto-Indo europeos (de los cuales la mayoría de los idiomas europeos y índicos descienden) podría haber sustituido un sistema de base de 8 (o un sistema que sólo podía contar hasta 8) con un sistema de base 10. La evidencia es que la palabra para 9, NEWM, es sugerido por algunos a derivar de la palabra para el "nuevo", newo-, lo que sugiere que el número 9 se había inventado recientemente y llamado el 'número nueva' (Mallory y Adams 1997) .

Diez

El sistema de base 10 ( decimal ) es el más comúnmente utilizado en la actualidad. Se supone que se originó porque los seres humanos tienen diez los dedos. Estos sistemas utilizan a menudo una base superpuesta más grande. Ver Superbase Decimal.

Doce

12-Base sistemas ( duodecimal o dozenal) han sido populares porque la multiplicación y la división son más fáciles que en base 10, con la adición y la sustracción de ser igual de fácil. 12 es una base útil porque tiene muchos factores . Es el múltiplo más pequeño de uno a cuatro y de seis. Todavía hay una palabra especial para "docena", y al igual que hay una palabra para 10 ^2, cien, también hay una palabra para 12 ^2, bruto. Base-12 podría haberse originado a partir del número de nudillos en los cuatro dedos de una mano excluyendo el pulgar, que se utiliza como un puntero en el conteo.

Doce es una unidad de medida común británica. Hay doce pulgadas a un pie. Antes de 1971, en la moneda británica, había 12 centavos a un chelín. . Las palabras en inglés para los números son también "base-12 'en que no es una palabra única para que los números del uno al doce, con' trece 'ser la primera palabra que se formó por la combinación de números (tres y diez).

Hay 24 horas al día, por lo general, contados hasta las 12 hasta el mediodía ( pm) y una vez más hasta la medianoche ( am), a menudo dividen a su vez por 6 horas en el conteo (por ejemplo, en Tailandia ) o como alterna entre el uso de términos como 'la noche', 'mañana', 'tarde', y 'la noche', mientras que otros idiomas usan tales términos con duraciones de 3 a 9 horas a menudo de acuerdo con interruptores en algunas de las marcas de intervalo de 3 horas.

Múltiplos de 12 han sido de uso común como unidades inglesas de resolución en el análogo y el mundo de la impresión digital, en la que 1 punto es igual a 1/72 de pulgada y 12 puntos es igual a 1 pica, y la impresora como resoluciones 360, 600, 720, 1200 o 1440 dpi (puntos por pulgada) son comunes. Estos son combinaciones de base 12 y la base 10-factores: (3 × 12) × 10, 12 × (5 × 10), (6 × 12) × 10, 12 × (10 × 10) y (12 × 12) × 10.

Veinte

La civilización maya y otras civilizaciones de Precolombino Mesoamérica utiliza de base-20 ( vigesimal), posiblemente procedente del número de dedos de manos y pies de una persona. Evidencia de sistemas de conteo de base-20 se encuentra también en los idiomas del centro y oeste de África .

También existen posibles restos de un sistema de base 20 en francés, como se ve en los nombres de los números del 60 al 99. Por ejemplo, el sesenta y cinco es soixante-cinq (literalmente, "sesenta [y] cinco"), mientras que setenta -cinco es soixante-quinze (literalmente, "sesenta [y] quince"). Además, para cualquier número entre 80 y 99, el número "decenas-columna" se expresa como un múltiplo de veinte (algo similar a la forma arcaica de Inglés habla de " puntajes "). Por ejemplo, el ochenta y dos es quatre-vingt-deux (literalmente, cuatro veinte [s] [y] dos), mientras que noventa y dos es quatre-vingt-douze (literalmente, cuatro veinte [s] [y ] doce).

La Lengua irlandesa también utilizó la base-20 en el pasado, veinte ser fichid, cuarenta Dhá fhichid, fhichid sesenta Tri y fhichid ceithre ochenta. Un remanente de este sistema puede ser visto en la palabra moderna para 40, daoichead.

Números daneses muestran una estructura de base similares-20.

Sesenta

Base 60 ( sexagesimal) fue utilizado por los sumerios y sus sucesores en Mesopotamia y sobrevive hoy en día en nuestro sistema de tiempo (de ahí la división de una hora en 60 minuto y un minuto en 60 segundos) y en nuestro sistema de medida angular (un grado se divide en 60 minuto y un minuto se divide en 60 segundos). 60 también tiene un gran número de factores, incluyendo los seis primeros números contables . Base-60 sistemas se cree que se originó a través de la fusión de la base-10 y la base-12 sistemas. La Calendario chino, por ejemplo, utiliza una base-60 Jia-Zi 甲子 sistema para denotar años, con cada año dentro del ciclo de 60 años de ser nombrado con dos símbolos, la base-10 el primer ser (llamado Tian-Gan 天干 o tallos celestiales) y el segundo símbolo que represente la base 12 (llamados Di-Zhi 地支 o ramas terrestres). Ambos símbolos se incrementan en los años sucesivos hasta que el primer patrón se repite 60 años después. El segundo símbolo de este sistema también está relacionado con el 12-animales Sistema del zodiaco chino. El sistema de Jia-zi también se puede aplicar a contar los días, con un año que contiene aproximadamente seis ciclos de 60 días.

La base dual (veinticinco)

Muchos sistemas de conteo antiguos utilizan 5 como base primaria, casi seguro que viene del número de dedos en la mano de una persona. A menudo, estos sistemas se complementan con una base secundaria, a veces diez, veinte veces. En algunos Lenguas africanas la palabra para 5 es la misma que la "mano" o "puño" ( Dyola lengua de Guinea-Bissau , Banda lengua de África Central). Conteo continúa mediante la adición de 1, 2, 3, o 4 a combinaciones de 5, hasta que se alcanza la base secundaria. En el caso de los veinte años, esta palabra a menudo significa "hombre completo". Este sistema se conoce como quinquavigesimal. Se encuentra en muchas lenguas del Sudán región.

Nombres de base

     1 -   unario 2 - binario 3 -   ternario / trinary 4 -   cuaternario 5 -   quinario / quinternary 6 -   senary /   heximal / hexary 7 -   septenario / septuary 8 -   octal / octonary / OCTONAL / octimal 9 -   nonary / novary / Noval 10 - decimal / denario 11 -   undecimal / undenary / unodecimal 12 -   dozenal / duodecimal / duodenario 13 -   tridecimal /   tredecimal / triodecimal 14 -   tetradecimal / quadrodecimal / quattuordecimal 15 -   pentadecimal / quindecimal 16 - hexadecimal / sexadecimal / sedecimal 17 - septendecimal / heptadecimal 18 - octodecimal / decennoctal 19 - nonadecimal / novodecimal / decennoval 20 -   vigesimal / bigesimal / bidecimal 21 - unovigesimal / unobigesimal 22 - duovigesimal 23 - triovigesimal 24 -   quadrovigesimal / quadriovigesimal 26 -   hexavigesimal / sexavigesimal 27 - heptovigesimal 28 - octovigesimal 29 - novovigesimal 30 -   trigesimal / triogesimal 31 - unotrigesimal (... repetición del patrón de nombres ...) 36 -   hexatridecimal / sexatrigesimal (... repetición nombrar patrón ...) 40 - cuadragesimal / quadrigesimal 41 - unoquadragesimal (... repetición nombrar patrón ...) 50 - quinquagesimal / pentagesimal 51 - unoquinquagesimal (... repetición del patrón de denominación .. .) 60 -   sexagesimal (... repetición nombrar patrón ...) 64 -   quadrosexagesimal (... repetición del patrón de nombres ...) 70 - septagesimal / heptagesimal 80 - octagesimal / octogesimal 90 - nonagesimal / novagesimal 100 - centimal / centesimal (... repetición del patrón de nombres ...) 110 - decacentimal 111 - unodecacentimal ( ... de la repetición de nombres ...) 200 - bicentimal / bicentesimal (... repetición nombrar patrón ...) 210 - decabicentimal 211 - unodecabicentimal (... repetición nombrar patrón ...) 300 - tercentimal / tricentesimal 400 - quattrocentimal / quadricentesimal 500 - quincentimal / pentacentesimal 600 - hexacentimal / hexacentesimal 700 - heptacentimal / heptacentesimal 800 - octacentimal / octocentimal / octacentesimal / octocentesimal 900 - novacentimal / novacentesimal 1000 - milesimal 2000 - bimillesimal (... repetición del patrón de nombres ...) 10.000 - decamillesimal

Sistemas posicionales en detalle

En un sistema de b basal posicional numeral (con b un positivo número natural conocido como el radix), se utilizan los símbolos b básicas (o dígitos) correspondientes a los primeros b números naturales incluyendo el cero. Para generar el resto de los números, se utiliza la posición del símbolo en la figura. El símbolo en la última posición tiene su propio valor, y ya que se mueve a la izquierda, su valor se multiplica por b.

Por ejemplo, en el decimal sistema (base 10), los medios 4327 numeral (4 × 10 ³⁾ + (3 × 10 ²⁾ + (2 × 10 ¹⁾ + (7 × 10 ^0), señalando que 10 ⁰ = 1 .

En general, si b es la base, se escribe un número en el sistema de numeración de base b expresándolo en forma a _n b ⁿ + a _{n - 1} b ^{n - 1} + a _{n - 2} b ^{n - 2} +. .. + a ₀ b ⁰ y escribir los dígitos enumerados a _n a _{n - 1} a _{n - 2} ... un ₀ en orden descendente. Los dígitos son números naturales entre 0 y b - 1, ambos inclusive.

Si un texto (como éste), examina las múltiples bases, y si existe ambigüedad, se añade la base (representación actúa en base 10) en el subíndice a la derecha del número, así: _{base numérica.} Salvo que se especifique por el contexto, números sin subíndice se consideran decimal.

Mediante el uso de un punto de dividir los dígitos en dos grupos, uno también puede escribir fracciones en el sistema posicional. Por ejemplo, la base-2 numeral 1 denota 10,11 × 2 + ¹ 0 ⁰ × 2 + 1 × 2 + 1 ^{-1 -2} × 2 = 2,75.

En general, los números en el sistema de base b son de la forma:

$(A_na_ {n-1} \ cdots a_1a_0.c_1 c_2 C_3 \ cdots) _b = \ sum_ {k = 0} ^ n a_kb ^ k + \ sum_ {k = 1} ^ \ infty c_kb ^ {- k}.$

El número b ^k y b ^{- k} son los pesos de los dígitos correspondientes. La posición k es el logaritmo del peso correspondiente w, es decir $k = \ log_ {b} w = \ log_ {b} b ^ k$ . La posición más alta utilizada está cerca de la orden de magnitud del número.

El número de marcas de conteo requiere en el sistema de numeración unario para describir el peso habría sido w. En el sistema posicional el número de dígitos necesarios para describir es sólo $k + 1 =$ $\ Log_ {b} w$ $+ 1$ , Para $k \ ge 0$ . Por ejemplo, para describir el peso se necesitan 1000 luego de 4 dígitos desde $\ Log_ {10} 1000 + 1 = 3 + 1$ . El número de dígitos necesarios para describir la posición es $\ Log_ {b} k + 1 = \ log_ {b} \ log_ {b} w + 1$ (En las posiciones 1, 10, 100 ... sólo por simplicidad en el ejemplo decimal).

Posición	3	2	1	0	-1	-2	...
Peso	$b ^ 3$	$b ^ 2$	$b ^ 1$	$b ^ 0$	$b ^ {- 1}$	$b ^ {- 2}$	...
Dígito	$a_3$	$a_2$	$a_1$	$a_0$	$c_1$	$c_2$	...
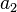Decimal ejemplo peso	1000	100	10	1	0.1	0.01	...
Ejemplo Decimal dígitos	4	3	2	7	0	0	...

Tenga en cuenta que un número tiene una terminación o repetición de expansión si y sólo si es racional ; esto no depende de la base. Un número que termina en una base puede repetir en otro (por lo tanto 0,3 ₁₀ = 0.0100110011001 ... _2). Un número irracional permanece unperiodic (número infinito de dígitos unrepeating) en todas las bases integrales. Así, por ejemplo, en la base 2, π = 3.1415926 ... ₁₀ puede escribirse como la unperiodic 11,001001000011111 ... _2.

Si b = p es un número primo , uno puede definir números p sótanos cuya expansión a la izquierda nunca se detiene; éstos se llaman el números p-adic.

Cambio de base

Un simple algoritmo para convertir enteros entre radices enteros positivos se repite la división por la raíz de destino; los restos dan los "dígitos" que empiezan en el menos significativo. Por ejemplo, 1020304 base 10 en la base 7:

 1020304/7 = 145 757 r 5
  145757/7 = 20822 r 3
   20822/7 = 2974 r 4
    2974/7 = 424 r 6
     424/7 = 60 r 4
      60/7 = 8 r 4
       8/7 = 1 r 1
       1/7 = 0 r = 1> 11446435

Por ejemplo, 10110111 base 2 en la base 5:

 10110111/101 = 100 100 r 11 (3)
   100100/101 = 111 r 1 (1)
      111/101 = 1 r 10 (2)
        1/101 = 0 r 1 (1) => 1213

Para convertir una fracción "decimal", hacer la multiplicación repetida, tomando las piezas enteras sobresalen como los "dígitos". Desafortunadamente una fracción de terminación en una base puede no terminar en otro. Por ejemplo, la base de 0.1A4C 16 en la base 9:

 0.1A4C × 9 = 0.ECAC 0.ECAC × 9 = 0.520C 8.520C × 9 = 0.E26C 2.E26C × 9 = 7.F5CC 0.F5CC × 9 = 0.A42C 8.A42C × 9 = 5. C58C => 0,082785 ...

Generalizadas enteros de longitud variable

Más en general está utilizando una notación (aquí escrito little-endian) como $a_0 a_1 a_2$ para $a_0 + a_1 b_1 + a_2 b_1 b_2$ , Etc.

Esto se utiliza en punycode, uno de cuyos aspectos es la representación de una secuencia de números enteros no negativos de tamaño arbitrario en la forma de una secuencia sin delimitadores, de "dígitos" de una colección de 36: az y 0-9, 0-25 y que representa 26-35, respectivamente. Un dígito inferior a un valor umbral de marca que es el dígito más significativo, de ahí el final del número. El valor de umbral depende de la posición en el número. Por ejemplo, si el valor de umbral para el primer dígito es b (es decir, 1) y luego una (es decir, 0) marca el final de la serie (que tiene un solo dígito), por lo que en número de más de un dígito de la gama es sólo b -9 (1-35), por lo tanto, el peso b ₁ es 35 en lugar de 36. Supongamos que los valores de umbral para el segundo y tercer dígitos son c (2), entonces el tercer dígito tiene un peso 34 × 35 = 1190 y tenemos la siguiente secuencia:

a (0), BA (1), CA (2), .., 9a (35), bb (36), cb (37), .., 9b (70), bca (71), .., 99a (1260), el BCB (1261), etc.

Tenga en cuenta que a diferencia de un sistema de numeración de base 35 regular, tenemos números como 9b donde 9 y B representan cada uno 35; sin embargo, la representación es única porque ac y aca no están permitidos.

La flexibilidad en la elección de los valores de umbral permite la optimización en función de la frecuencia de aparición de los números de diferentes tamaños.

El caso con todos los valores de umbral igual a 1 corresponde a biyectiva numeración, donde los ceros corresponden a los separadores de los números con los dígitos que son no cero.

Propiedades de los sistemas numéricos con bases enteros

Sistemas de numeración con base A, donde A es un entero positivo, poseer las siguientes propiedades:

Si A es par y A / 2 es impar, todos los poderes integrales superior a cero del número (A / 2) 1 contendrán (A / 2) 1 como último dígito

Si tanto A como A / 2 son aún, a continuación, todas las potencias enteras mayor que o igual a cero de la serie (A / 2) +1 alternará entre que tiene (A / 2) 1 y 1 como su último dígito. (Para potencias impares será (A / 2) 1, incluso para los poderes que habrá 1)

Prueba de la primera propiedad:

Definir ${A \ over 2} + 1 = x$ Entonces x es par, y todo $x ^ p$ para p mayor que 0 debe ser par. La propiedad es equivalente a

$\! \ X ^ p \ equiv \ x \ (\ mbox {mod} \ A)$

En primer lugar, comprobamos el caso de p = 1

$\! \ X \ equiv \ x \ (\ mbox {mod} \ A)$

x es menor que A, por lo que el resultado es trivial. A continuación, comprobar para p = 2:

$\! \ X ^ 2 = xx$

$\! \ X ^ 2 = x (x-1) + x$

Desde $x-1 = ({A \ over 2} + 1) - 1 = {A \ over 2}$ , Entonces para todo incluso N:

$\! \ {NA \ over 2} = N (x-1) \ equiv \ 0 \ (\ mbox {mod} \ A) \ (1)$

Debido a que x es par, entonces $x (x-1)$ es congruente con módulo cero A. Por lo tanto:

$\! \ X ^ 2 \ equiv \ x \ (\ mbox {mod} \ A)$

Uso de inducción, suponiendo que la propiedad se mantiene para p -1:

$\! \ X ^ {p = x ^ {p-1}} x = {x ^ {p-1}} (x-1) + x ^ {p-1}$

Dado el caso se mantiene para p -1, entonces ${X ^ {p-1}} \ equiv \ x \ (\ mbox {mod} \ A)$ . Desde

$\! \ {X ^ {p-1}} (x-1)$

es un caso de la Ecuación 1, a continuación, ${X ^ {p-1}} (x-1) \ equiv \ 0 \ (\ mbox {mod} \ A)$ . Esto deja, para todo p mayor que 0,

$\! \ X ^ p \ equiv \ x \ (\ mbox {mod} \ A)$

QED

Prueba de la segunda propiedad:

Definir ${A \ over 2} + 1 = x$ Entonces x es impar, y todo $x ^ p$ para p mayor que o igual a 0 debe ser impar. La propiedad es equivalente a

$! \ \ X ^ p \ equiv \ 1 \ (\ mbox {mod} \ A); \ \ mbox {si} \ p \ equiv \ 0 \ (\ mbox {mod} \ 2)$

$! \ \ X ^ p \ equiv \ x \ (\ mbox {mod} \ A); \ \ mbox {si} \ p \ equiv \ 1 \ (\ mbox {mod} \ 2)$

Desde $x-1 = ({A \ over 2} + 1) - 1 = {A \ over 2}$ , Entonces para todos los impares E:

$\! \ {EA \ over 2} = E (x-1) \ equiv \ {A \ over 2} \ (\ mbox {mod} \ A) \ (2)$

El caso pasará primero para p = 0:

$\! \ X ^ 0 = 1$

$\! \ 1 \ equiv \ 1 \ (\ mbox {mod} \ A)$

Este resultado es trivial

A continuación, para p = 1:

$\! \ X ^ 1 = x$

$\! \ X \ equiv \ x \ (\ mbox {mod} \ A)$

Este resultado también es trivial

A continuación, para p = 2:

$\! \ X ^ 2 = xx = x (x-1) + x$

Debido a que x es impar, entonces x (x-1) es un caso de la Ecuación 2,

$x (x-1) + x \ equiv \ {{A \ over 2} + x} \ (\ mbox {mod} \ A)$

$\! \ {A \ over 2} + x = {A \ over 2} + {A \ over 2} + 1 = A + 1$

$\! \ A + 1 \ equiv \ 1 \ (\ mbox {mod} \ A), (\ mbox {so} \ x (x-1) + x = x ^ 2 \ equiv \ 1 \ (\ mbox {mod } \ A)$

A continuación, para p = 3:

$\! \ X ^ 3 = {x ^ 2} x = {x ^ 2} (x-1) + x ^ 2$

Porque $x ^ 2$ es impar, ${X ^ 2} (x-1) + x ^ 2$ es un caso de la Ecuación 2,

$\! \ {X ^ 2} (x-1) + x ^ 2 \ equiv \ {{A \ over 2} + x ^ 2} \ (\ mbox {mod} \ A)$

Desde $x ^ 2 \ equiv \ 1 \ (\ mbox {mod} \ A)$ ,

$\! \ {X ^ 2} (x-1) + x ^ 2 \ equiv \ {{A \ over 2} + 1} \ (\ mbox {mod} \ A)$

${{A \ over 2} + 1} = x$ , Por lo $x ^ 3 \ equiv \ x \ (\ mbox {mod} \ A)$ .

Uso de inducción, suponiendo que la propiedad se mantiene para p -1:

$\! \ X ^ p \ equiv \ {x ^ {p-1}} (x-1) + x ^ {p-1}$

Si p es impar:

$\! \ X ^ {p-1} \ equiv \ 1 \ (\ mbox {mod} \ A)$

Desde ${X ^ {p-1}} (x-1)$ es un caso de la ecuación (2), ${X ^ {p-1}} (x-1) + x ^ {p-1} \ equiv \ {{A \ over 2} + 1} \ (\ mbox {mod} \ A)$ , Por lo

$x ^ p \ equiv \ x \ (\ mbox {mod} \ A)$

Si p es par:

$\! \ X ^ {p-1} \ equiv \ x \ (\ mbox {mod} \ A)$

Desde ${X ^ {p-1}} (x-1)$ es un caso de la ecuación (2), ${X ^ {p-1}} (x-1) + x ^ {p-1} \ equiv \ {{A \ over 2} + x} \ (\ mbox {mod} \ A)$ .

${A \ over 2} + x = {A \ over 2} + {A \ over 2} + 1 = A + 1$

$A + 1 \ equiv \ 1 \ (\ mbox {mod} \ A)$ , Por lo

$x ^ p \ equiv \ 1 \ (\ mbox {mod} \ A)$

QED

Recuperado de " http://en.wikipedia.org/w/index.php?title=Numeral_system&oldid=197894673 "

See also ebooksgratis.com: no banners, no cookies, totally FREE.