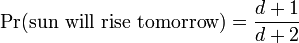Pierre-Simon Laplace

Pierre-Simon, marqués de Laplace
Retrato póstumo de Madame Feytaud de 1842
Nacido	23/03/1749 Beaumont-en-Auge, Normandía, Francia
Murió	05 de marzo 1827 (03/05/1827) (77 años) París , Francia
Residencia	Francia
Ciudadanía	Francés
Campos	Astronomía Matemáticas
Instituciones	École Militaire (1769-1776)
Conocido por	Trabajar en Mecánica Celeste La ecuación de Laplace Laplace Operador / Laplaciano Transformada de Laplace

Pierre-Simon, marqués de Laplace ( 23 de marzo 1749 - 05 de marzo 1827 ) fue un francés matemático y astrónomo cuya labor fue fundamental para el desarrollo de la astronomía matemática . Resumió y amplió el trabajo de sus predecesores en su cinco volúmenes Mécanique Céleste ( Mecánica Celeste) (1799-1825). Este trabajo seminal tradujo el geométrica estudio de la mecánica clásica , utilizado por Isaac Newton , a una basada en el cálculo , la apertura de una gama más amplia de problemas.

Formuló La ecuación de Laplace, e inventó el Transformada de Laplace, que aparece en muchas ramas de la física matemática , un campo que él tomó un papel de liderazgo en la formación. La Operador diferencial de Laplace, ampliamente utilizado en la aplicada matemáticas , también lleva su nombre.

Independientemente de Immanuel Kant , formuló la hipótesis nebular de la origen del sistema solar, y fue uno de los primeros científicos a postular la existencia de los agujeros negros y la noción de colapso gravitacional.

Se le recuerda como uno de los más grandes científicos de todos los tiempos, a veces referido como un francés Newton o Newton de Francia, con una facultad matemática fenomenal naturales que posee ninguno de sus contemporáneos.

Se convirtió en un contar de la Primer Imperio francés en 1806 y fue nombrado un marqués en 1817, después de la Restauración borbónica.

Primeros años de vida

Pierre Simon Laplace nació en Beaumont-en-Auge, Normandía.

De acuerdo a Rouse Ball ('Brevísima relación de la historia de las matemáticas', cuarta edición, 1908), que era el hijo de un pequeño aldeano o tal vez una granja-obrero, y debía su educación al interés emocionado en algunos vecinos ricos por sus habilidades y la presencia de acoplamiento. Muy poco se sabe de sus primeros años, para cuando llegó a ser distinguido que tenía la mezquindad que se apartaba tanto de sus parientes y de los que le habían ayudado. Al parecer, según un alumno se convirtió en un ujier en la escuela de Beaumont; pero, después de haber adquirido una carta de presentación a D'Alembert, se trasladó a París para empujar su fortuna. Sin embargo, Pearson (1929, Biometrika) es mordaz sobre las inexactitudes en la cuenta de Rouse Ball y afirma que ".. Caen fue probablemente en la época de Laplace los intelectualmente activa de todos los pueblos de Normandía más. Fue aquí que Laplace fue educado y fue provisionalmente profesor. Fue aquí Escribió su primer artículo publicado en los Melanges del Sociedad Real de Turín, iv Tomé. 1766-1769, al menos dos años antes de ir a 22 o 23 a París en 1771. Por lo tanto, antes era de 20 que estaba en contacto con Joseph Louis Lagrange en Turín . Él no fue a París un autodidacta país muchacho crudo con sólo un fondo campesino I En 176S a la edad de dieciséis años Laplace dejó la "Escuela del duque de Orleans" en Beaumont y se fue a la Universidad de Caen, donde aparece haber estudiado durante cinco años. El "Ecole Militaire" de Beaumont no reemplazó la vieja escuela hasta 1770.

Su padre fue Pierre Laplace, una sidra comerciante y su madre fue Marie-Anne Barrio Sochon. Sus padres eran de cómodo familias burguesas. Laplace asistió a una escuela en la aldea de ejecución en un Benedictino priorato, su padre la intención de que sería ordenado en la Iglesia Católica Romana , ya los dieciséis fue enviado a promover la intención de su padre en el Universidad de Caen, lectura teología.

En la universidad, fue apadrinado por dos profesores entusiastas de las matemáticas, Christophe Gadbled y Pierre Le Canu, que despertaron su celo por el tema. Laplace nunca se graduó en teología, pero dejó de París con una carta de presentación de Le Canu a Jean le Rond d'Alembert. Hay una historia apócrifa que, de diecinueve años de edad, él solucionó el problema durante la noche que D'Alembert lo establecido para la presentación de la semana siguiente, luego resuelto un problema más difícil de la noche siguiente. D'Alembert estaba impresionado y lo recomendó para un lugar de enseñanza en el École Militaire.

Con un ingreso seguro y la enseñanza poco exigente, Laplace ahora se lanzó a la investigación original y, en los diecisiete años siguientes, 1771-1787, él produjo mucho de su trabajo original en la astronomía.

Laplace impresionó aún más el Marqués de Condorcet, e incluso en 1771 Laplace sentía que tenía derecho a ser miembro de la Academia de Ciencias francés. Sin embargo, en ese año, el ingreso fue a Alexandre-Théophile Vandermonde y en 1772 a Antoine-Joseph primo. Laplace estaba disgustado y principios de 1773 sondeó un traslado a Berlín . Sin embargo, Condorcet se convirtió en secretario permanente de la Academia en febrero y Laplace fue elegido miembro asociado en 31 de marzo.

Se casó en 1788 y su hijo nació en 1789.

Análisis, probabilidad y la estabilidad astronómico

Obra publicada a principios de Laplace en 1771 comenzó con ecuaciones diferenciales y diferencias finitas, pero él ya estaba empezando a pensar en los conceptos matemáticos y filosóficos de probabilidad y estadística . Sin embargo, antes de su elección a la Academia en 1773, ya había elaborado dos documentos que permitan establecer su reputación. El primero, Mémoire sur la probabilité des provoca les événements par se publicó finalmente en 1774, mientras que el segundo artículo, publicado en 1776, elaboró aún más su pensamiento estadístico y también comenzó su trabajo sistemático en mecánica celeste y la estabilidad del sistema solar . Las dos disciplinas siempre estarían vinculados entre sí en su mente. "Laplace tuvo la probabilidad como un instrumento para la reparación de defectos en el conocimiento." El trabajo de Laplace en probabilidad y estadística se discute más adelante con su obra de madurez en la teoría analítica de las probabilidades.

La estabilidad del sistema solar

Sir Isaac Newton publicó su Philosophiae Naturalis Principia Mathematica en 1687 en el que daba una derivación de las leyes de Kepler , que describen el movimiento de los planetas , de sus leyes del movimiento y su la ley de la gravitación universal. Sin embargo, a pesar de que Newton había desarrollado de forma privada los métodos de cálculo , toda su obra publicada utiliza engorroso geométrica razonamiento, no aptos para dar cuenta de los efectos de orden superior más sutiles de las interacciones entre los planetas. Newton mismo había puesto en duda la posibilidad de una solución matemática a la totalidad, incluso concluyendo que periódica intervención divina era necesaria para garantizar la estabilidad del sistema solar. Prescindiendo de la hipótesis de la intervención divina sería la principal actividad de la vida científica de Laplace. A partir de 2007, se considera generalmente que los métodos de Laplace por su cuenta, aunque críticos para el desarrollo de la teoría, no son lo suficientemente precisa para demostrar la estabilidad del sistema solar.

Un problema particular de astronomía observacional fue la inestabilidad aparente por el que Júpiter orbita 's parecía estar disminuyendo mientras que la de Saturno se expandía. El problema había sido abordado por Leonhard Euler en 1748 y Joseph Louis Lagrange en 1763, pero sin éxito. En 1776, Laplace publicó una memoria en la que exploró por primera vez la posible influencia de un supuesto éter lumínico o de una ley de la gravitación que no actuó de forma instantánea. Él finalmente regresó a una inversión intelectual en la gravedad newtoniana. Euler y Lagrange habían hecho una aproximación práctica al ignorar pequeñas términos en las ecuaciones de movimiento. Laplace señaló que aunque los propios términos eran pequeños, cuando integrada sobre el tiempo que podían vuelven importantes. Laplace realiza su análisis en los términos de orden superior, hasta e incluyendo el cúbico. El uso de este análisis más exacto, Laplace llegó a la conclusión de que los dos planetas y el sol deben estar en equilibrio mutuo y con ello inició su trabajo en la estabilidad del sistema solar. Gerald James Whitrow describió el logro como "el avance más importante en la astronomía física desde Newton".

Laplace tenía un amplio conocimiento de todas las ciencias y dominó todos los debates de la Academia. Laplace parece haber considerado análisis meramente como un medio para atacar los problemas físicos, aunque la capacidad con la que inventó el análisis necesario es casi fenomenal. Mientras sus resultados eran ciertos, pero él tomó problemas para explicar los pasos por los que llegó a ellos; nunca estudió la elegancia o la simetría en sus procesos, y era suficiente para él si podía de ninguna manera resolver la cuestión particular, que estaba discutiendo.

En la figura de la Tierra

Durante los años 1784-1787 se produjo algunas memorias de potencia excepcional. Destacan entre ellos es una lectura en 1783, reeditado como la Parte II de Théorie du Mouvement et de la figura elliptique des planètes en 1784, y en el tercer volumen de la céleste Méchanique. En este trabajo, Laplace completamente determinado la atracción de un esferoide sobre una partícula fuera de ella. Esta es memorable por la introducción en el análisis de armónicos esféricos o Laplace de coeficientes, y también para el desarrollo de la utilización de la potencial, un nombre usado por primera vez por George Green en 1828.

Armónicos esféricos

Armónicos esféricos

En 1783, en un documento enviado a la Academia, Adrien-Marie Legendre había introducido lo que ahora se conoce como funciones asociadas de Legendre. Si dos puntos en un plano tienen coordenadas polares (r, θ) y (r ', θ'), donde r '≥ r, entonces, por la manipulación elemental, el recíproco de la distancia entre los puntos, d, puede haber escrita como:

Esta expresión puede ser ampliado en potencias de r / r 'usando Teorema binomial generalizado de Newton para dar:

La secuencia de las funciones P ⁰ _k (cosф) es el conjunto de los llamados "funciones de Legendre asociadas" y su utilidad surge del hecho de que cada función de los puntos de un círculo puede ser expandido como una serie de ellos.

Laplace, con escaso respeto por el crédito a Legendre, hizo que la extensión no trivial de que el resultado tres dimensiones para producir un conjunto más general de las funciones, los armónicos esféricos o coeficientes de Laplace. A partir de 2007, este último término no es de uso común. Cada función de los puntos de una esfera se puede ampliar como una serie de ellos.

La teoría del potencial

Este documento también destaca por el desarrollo de la idea de la potencial escalar. El gravitacional fuerza que actúa sobre un cuerpo es, en lenguaje moderno, un vector , que tiene magnitud y dirección. Una función potencial es una función escalar que define cómo los vectores se comportarán. Una función escalar es computacionalmente y conceptualmente más fácil de tratar que una función vectorial.

Alexis Clairault había sugerido la idea en 1743 mientras trabajaba en un problema similar, aunque él estaba usando de tipo newtoniano razonamiento geométrico. Laplace describió el trabajo de Clairault como "en la clase de las más bellas producciones matemáticas". Sin embargo, Rouse Bola alega que la idea "se apropió de Joseph Louis Lagrange , que había utilizado en sus memorias de 1773, 1777 y 1780 ".

Laplace aplica el lenguaje del cálculo a la función potencial y muestra que siempre satisface la ecuación diferencial :

- Y en este resultado se basó su trabajo posterior en la atracción gravitacional. La cantidad que se ha denominado la concentración de y su valor en cualquier punto indica el "exceso" del valor de hay más de su valor medio en el entorno del punto. La ecuación de Laplace, un caso especial de La ecuación de Poisson, aparece de forma ubicua en la física matemática. Cada vez que un vector de fuerza actúa sobre un cuerpo, el concepto de un potencial pueden ser aplicados y la ecuación de Laplace se produce en dinámica de fluidos, electromagnetismo y otras áreas. Según algunos autores esto sigue a la vez del hecho de que es un operador escalar. Rouse Bola especuló que podría ser visto como "el signo externo" de uno de los "formularios anteriores" en la teoría de la percepción de Kant .

Los armónicos esféricos resultan ser críticos para soluciones prácticas de la ecuación de Laplace. La ecuación de Laplace en coordenadas esféricas , como se utilizan para el mapeo de la cielo, se puede simplificar, usando el método de la separación de variables en una parte radial, dependiendo únicamente de distancia de la Tierra (por ejemplo), y una parte angular o esférica. La solución a la parte esférica de la ecuación se puede expresar como una serie de armónicos esféricos de Laplace, lo que simplifica el cálculo práctico.

Desigualdades planetarias

Esta memoria fue seguido por otro en las desigualdades planetarias, que se presentó en tres secciones en 1784, 1785 y 1786. Este trabajo trata principalmente con la explicación de la "gran desigualdad" de Júpiter y Saturno. Laplace mostró por consideraciones generales que la acción mutua de dos planetas nunca podría afectar en gran medida las excentricidades e inclinaciones de sus órbitas; y que las peculiaridades del sistema joviano se debieron a la cercanía a la conmensurabilidad de los movimientos medios de Júpiter y Saturno: la evolución de estos teoremas sobre el movimiento planetario se dan en sus dos memorias de 1788 y 1789. Fue en estos datos que Delambre calcula sus tablas astronómicas.

Se había observado desde la antigüedad que la Luna posición 's en el cielo iba a la deriva con el tiempo. En 1693, Edmond Halley había demostrado que la tasa de la deriva fue en aumento, un efecto conocido como la aceleración secular de la Luna. Laplace dio una explicación en 1787 en términos de cambios en la excentricidad de la órbita de la Tierra. Sin embargo, en 1853, John Couch Adams llegó a demostrar que Laplace sólo había considerado la fuerza radial en la luna y no el tangencial, y por lo tanto no había explicado más de la mitad de la deriva. La otra mitad se demostró posteriormente que se debe a aceleración de marea. Sin embargo, Laplace todavía era capaz de usar su resultado para completar la prueba de la la estabilidad de todo el sistema solar en el supuesto de que consiste en una colección de cuerpos rígidos en movimiento en un vacío.

Todas las memorias anteriormente aludidas fueron presentadas a la Academia de las ciencias, y que se imprimen en el Mémoires Presentes buzos par sabios.

Mecánica celeste

Laplace ahora se impuso la tarea de escribir una obra que debe "ofrecer una solución completa de la gran problema mecánico presentado por el sistema solar , y llevar la teoría a coincidir muy de cerca con la observación de que las ecuaciones empíricas ya no deben encontrar un lugar en las tablas astronómicas. " El resultado se plasma en la Exposición du système du monde y la céleste Mécanique.

El primero fue publicado en 1796, y da una explicación general de los fenómenos, pero omite todos los detalles. Contiene un resumen de la historia de la astronomía. Este resumen procuró para su autor el honor de admisión a los cuarenta de la Academia Francesa y es comúnmente apreciado una de las obras maestras de la literatura francesa, aunque no es del todo fiable para los períodos posteriores de las que trata.

Laplace desarrolló el hipótesis nebular de la formación del sistema solar, primero sugerido por Emanuel Swedenborg y ampliado por Immanuel Kant , una hipótesis que sigue dominando cuentas del origen de los sistemas planetarios. Según la descripción de Laplace de la hipótesis, el sistema solar había evolucionado a partir de una masa globular de incandescente de gas que gira alrededor de un eje a través de su centro de masa . Como se enfría esta masa se contrajo y anillos sucesivos se separó de su borde exterior. Estos anillos a su vez enfriados, y finalmente condensan en los planetas , mientras que el sol representa el núcleo central que aún quedaba. En esta vista Laplace predijo que los planetas más distantes serían más antiguas que las más cerca del sol.

La idea de la hipótesis nebular había sido esbozada por Immanuel Kant en 1755, y él también había sugerido "agregaciones meteóricos" y fricción de las mareas como las causas que afectan a la formación del sistema solar. Es probable que Laplace no era consciente de ello.

Discusión analítica de Laplace del sistema solar se da en su céleste Méchanique publicada en cinco volúmenes. Los dos primeros volúmenes, publicados en 1799, contienen métodos para calcular los movimientos de los planetas, la determinación de sus figuras, y la resolución de problemas de marea. El tercer y cuarto volúmenes, publicados en 1802 y 1805, contienen aplicaciones de estos métodos, y varias tablas astronómicas. El quinto volumen, publicado en 1825, es principalmente histórico, pero da como apéndices de los resultados de las últimas investigaciones de Laplace. Las propias investigaciones de Laplace consagrados en ella son tan numerosas y valiosa que es lamentable tener que añadir que muchos resultados se apropiaron de los escritores con escaso o ningún reconocimiento, y las conclusiones - que han sido descritos como el resultado organizada de un siglo de trabajo paciente - se mencionan con frecuencia como si fueran causa de Laplace.

Jean-Baptiste Biot, que ayudó Laplace en la revisión de la prensa, dice que el propio Laplace era con frecuencia incapaz de recuperar los datos de la cadena de razonamiento, y, si estima que las conclusiones eran correctas, estaba contenido para insertar el constante recurrente fórmula, "Il est AISE à voir". El céleste Méchanique no es sólo la traducción de los Principia en el idioma del cálculo diferencial, sino que completa algunas de cuyas partes Newton no había podido completar los detalles. El trabajo fue más finamente sintonizado por Félix Tisserand pero el tratado de Laplace siempre seguirán siendo una autoridad estándar.

Casa de Laplace en Arcueil

Arcueil

En 1806, Laplace compró una casa en Arcueil, entonces un pueblo y aún no absorbidos en el París conurbación. Claude Louis Berthollet fue un vecino cercano y el par formó el núcleo de un círculo científica informal, últimamente conocido como la Sociedad de Arcueil. A causa de Laplace y de Berthollet cercanía a Napoleón , que controlaban efectivamente el avance en la creación científica y la entrada a las oficinas más prestigiosos. La Sociedad construyó un complejo de pirámides de patrocinio.

La ciencia como predicción

Laplace fue en el estado de mendigar Napoleón a aceptar una copia de su obra, que había oído que el libro contenía ninguna mención de Dios . Napoleón, que era aficionado a formular preguntas embarazosas, lo recibió con el comentario, "M. Laplace, me han dicho que ha escrito este gran libro sobre el sistema del universo, y ni siquiera han mencionado su Creador." Laplace, quien, aunque el más flexible de los políticos, era tan rígida como un mártir en cada punto de su filosofía, se irguió y respondió sin rodeos: "Je n'avais pas besoin de cette hypothèse-là." (Yo no necesito para hacer tal suposición). Napoleón, enormemente divertido, dijo a esta respuesta al Lagrange, quien exclamó: "Ah c'est une belle hypothèse;! Ça explique beaucoup de choses" (Ah que es una hermosa hipótesis;! Explica muchas cosas). Laplace declaró entonces: "Cette hypothèse, Sire, explique en effet tout, mais ne permet de prédire rien En tant que savant, je me dois de vous Fournir des travaux permettant des predicciones." ("Esta hipótesis, señor, no lo explica todo, pero no permite a predecir nada. Como erudito, debo ofrecerle obras que permiten predicciones. "- Citado por Ian Stewart y Jack Cohen) Laplace ciencia así definida como una herramienta de predicción..

Los agujeros negros

Laplace también estuvo cerca de proponiendo el concepto de agujero negro . Señaló que no puede haber estrellas masivas cuya gravedad es tan grande que ni siquiera la luz puede escapar de su superficie (ver velocidad de escape). Laplace también especuló que algunas de las nebulosas revelado por los telescopios pueden no ser parte de la Vía Láctea y en realidad podría ser propias galaxias. De este modo, anticipó el gran descubrimiento de Edwin Hubble, unos 100 años antes de que sucediera.

La teoría analítica de las probabilidades

En 1812, Laplace publicó sus Théorie des analytique probabilités en que él dio muchos resultados fundamentales en las estadísticas . En 1819, publicó un relato popular de su obra en la probabilidad. Este libro tiene la misma relación con la Théorie des probabilités que el Système du monde hace al céleste Méchanique.

Función de probabilidad de generación de

El método de estimación de la relación entre el número de casos favorables, en comparación con el número total de casos posibles, se había indicado previamente por Laplace en un documento escrito en 1779. Consiste en el tratamiento de los valores sucesivos de cualquier función como los coeficientes de la expansión de otra función, con referencia a una variable diferente. Por tanto, el último se llama el función de probabilidad de generación de la primera. Laplace a continuación, muestra cómo, por medio de interpolación , estos coeficientes pueden ser determinados a partir de la función generatriz. Siguiente ataca el problema inverso, ya partir de los coeficientes se encuentra la función de generación; esto se efectúa por la solución de una ecuación de diferencias finitas. El método es engorroso y lleva la mayor parte del tiempo a una distribución de probabilidad normal de la llamada distribución de Laplace-Gauss, que no debe confundirse con el Distribución de Laplace.

Mínimos cuadrados

Este tratado incluye una exposición del método de mínimos cuadrados , un testimonio notable al mandato de Laplace en los procesos de análisis. El método de los mínimos cuadrados para la combinación de numerosas observaciones habían dado empíricamente por Carl Friedrich Gauss y Legendre, pero el cuarto capítulo de este trabajo contiene una prueba formal de la misma, en la que se ha basado el conjunto de la teoría de los errores desde entonces. Esto se ve afectado únicamente por un análisis más intrincado especialmente inventada para este fin, pero la forma en la que se presenta es tan escaso e insatisfactorio que, a pesar de la exactitud uniforme de los resultados, fue en un tiempo cuestionado si Laplace tenía realmente pasado por el difícil trabajo que tan brevemente y, a menudo incorrectamente indica.

Probabilidad inductiva

Mientras que él llevó a cabo mucha investigación en la física , otro tema importante de los esfuerzos de su vida era la teoría de probabilidades . En su Essai sur les filosófico probabilités, Laplace establece un sistema matemático de razonamiento inductivo basado en la probabilidad , que tendríamos hoy reconocer como Bayesiano. Una fórmula muy conocida a raíz de su sistema es el regla de sucesión. Supongamos que un poco de ensayo sólo tiene dos resultados posibles, con la etiqueta "éxito" y "fracaso". Bajo el supuesto de que poco o nada se sabe a priori acerca de las verosimilitudes relativas de los resultados, Laplace deriva una fórmula para la probabilidad de que la próxima prueba será un éxito.

donde s es el número de éxitos observados anteriormente y n es el número total de ensayos observados. Todavía se utiliza como un estimador de la probabilidad de un evento si conocemos el espacio para eventos, pero sólo tienen un pequeño número de muestras.

La regla de la sucesión ha sido objeto de muchas críticas, en parte debido al ejemplo que Laplace eligió para ilustrarlo. Se calcula que la probabilidad de que el sol saldrá mañana, dado que nunca ha fallado en el pasado, era

donde d es el número de veces que el sol ha salido en los últimos tiempos. Este resultado ha sido ridiculizado como absurda, y algunos autores han llegado a la conclusión de que todas las aplicaciones de la Regla de Sucesión son absurdas por extensión. Sin embargo, Laplace era plenamente consciente de lo absurdo de los resultados; inmediatamente después del ejemplo, escribió: "Pero este número [es decir, la probabilidad de que el sol saldrá mañana] es mucho mayor para él que, viendo en la totalidad de los fenómenos que regulan el principio de los días y las estaciones, se da cuenta de que nada en el momento presente puede detener el curso de la misma ".

Demonio de Laplace

Laplace creía firmemente en determinismo causal, que se expresa en la siguiente cita de la introducción a la Essai:

Esta inteligencia se refiere a menudo como el demonio de Laplace (en la misma línea que El demonio de Maxwell). Tenga en cuenta que la descripción de la inteligencia hipotético descrito anteriormente por Laplace como una demonio no viene de Laplace, pero a partir de los biógrafos posteriores: Laplace veía a sí mismo como un científico que espera que la humanidad progresaría en una mejor comprensión científica del mundo, que, si y cuando finalmente completado, todavía tendría un enorme poder de cálculo para calcular todo en un solo instante.

Transformadas de Laplace

Ya en 1744, Euler, seguido de Lagrange, había empezado a buscar soluciones de ecuaciones diferenciales en la forma:

y .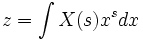

En 1785, Laplace dio el paso adelante clave en el uso integrales de esta forma con el fin de transformar su conjunto ecuación en diferencias, en lugar de simplemente como una forma de la solución, y encontró que la ecuación transformada era más fácil de resolver que el original.

Otros descubrimientos y logros

Matemáticas

Entre otros descubrimientos de Laplace en matemáticas puras y aplicables son:

• Discusión, contemporáneamente con Alexandre-Théophile Vandermonde, de la teoría general de los determinantes , (1772);
• La prueba de que toda ecuación de un grado aún debe tener al menos un verdadero factor cuadrático;
• Solución de la ecuación diferencial de segundo orden;
• Él fue el primero en considerar los difíciles problemas que intervienen en las ecuaciones de diferencias mixtas, y para demostrar que la solución de una ecuación en diferencias finitas de primer grado y de segundo orden puede siempre obtuvo en forma de un fracción continua; y
• En su teoría de las probabilidades:
  • Evaluación de varios comunes integrales definidas ; y
  • Prueba general de la Lagrange teorema de reversión.

Tensión superficial

Laplace basó en el trabajo cualitativo de Thomas Young para desarrollar la teoría de la acción capilar y la Ley de Laplace.

Velocidad del sonido

Laplace en 1816 fue el primero en señalar que el velocidad del sonido en el aire depende de la relación de capacidad de calor. La teoría original de Newton dio un valor muy bajo, ya que no toma en cuenta la adiabático compresión del aire que resulta en un aumento local en la temperatura y presión. Las investigaciones de Laplace en física práctica se limitaban a las realizadas por él conjuntamente con Lavoisier en los años 1782-1784 en el calor específico de diversos órganos.

Las ambiciones políticas

Como el poder de Napoleón aumentó Laplace le rogó que le diera el cargo de Ministro del Interior. Napoleón, que desea el apoyo de hombres de ciencia, aceptó la propuesta, pero un poco menos seis semanas vio el cierre de la carrera política de Laplace. Memorando de Napoleón en su despido es el siguiente:

Géomètre de premier sonó, Laplace ne pas à se tarda montrer administrateur médiocre plus que; dès hijo premier travail nous reconnûmes que nous nous étions trompé. Laplace saisissait ne aucune cuestión hijo sous point de vue véritable: il cherchait des subtilités partout, n'avait Que des idées problématiques, et Portait enfin l'esprit des `infiniment petits 'jusque dans l'administración. (Geómetra de primer orden, Laplace no tardó en mostrarse una peor que el administrador promedio; desde sus primeras acciones en el cargo reconocimos nuestro error Laplace no consideró ninguna cuestión objetiva: buscó sutilezas en todas partes, los problemas sólo concebidos, y, por último. llevado el espíritu de "sutilezas" en la administración.)

Aunque Laplace fue destituido de su cargo era deseable para retener su lealtad. Fue en consecuencia planteó al Senado, y para el tercer volumen de la Mécanique Céleste le antepone una nota que de todas las verdades contenidas en ella el más preciado para el autor era la declaración de él estas cosas en su devoción hacia el pacificador de Europa. En ejemplares vendidos después de la Restauración borbónica esto se ponchó. En 1814 era evidente que el imperio estaba cayendo; Laplace se apresuró a licitar sus servicios a la Borbones, y en la restauración fue recompensado con el título de marqués. El desprecio que sus colegas más honestas sentían por su conducta en el asunto podrá ser leído en las páginas de Paul Louis Courier. Su conocimiento era útil en las numerosas comisiones científicas en las que se desempeñó, y probablemente para explicar la manera en que se pasó por alto su falta de sinceridad política; pero la mezquindad de su personaje no debe hacernos olvidar lo grande que eran sus servicios a la ciencia.

Murió en París en 1827.

Honores

• Asteroide 4628 Laplace se nombra para él.
• Él es uno de sólo setenta y dos personas a tener sus nombres en la Torre Eiffel.

Comillas

Wikiquote tiene una colección de citas relacionadas con: Pierre-Simon Laplace

• Lo que sabemos no es mucho. Lo que no sabemos es inmensa. (Atribuido)
• No tenía ninguna necesidad de esa hipótesis. ("Je n'avais pas besoin de cette hypothèse-là", como una respuesta a Napoleón , que había preguntado por qué no había mencionado a Dios en su libro sobre astronomía )
• "Por tanto, es obvio que ..." (utilizado frecuentemente en la Mecánica Celeste cuando él había probado algo y extraviado la prueba, o que se encuentran es torpe. Notorious como una señal de algo cierto, pero difícil de probar.)
• El peso de la evidencia para una afirmación extraordinaria debe ser proporcional a su rareza. (Conocido como el Principio de Laplace)