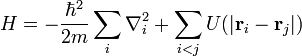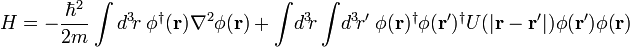Teoría cuántica de campos
Antecedentes de las escuelas de Wikipedia
SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . Visite el sitio web de Aldeas Infantiles SOS en http://www.soschildren.org/
| Teoría cuántica de campos |
|---|
 Diagrama de Feynman |
| Historia |
Fondo
|
Simetrías
|
Instrumentos
|
Ecuaciones
|
|
Teorías incompletas
|
Los científicos
|
Teoría cuántica de campos (QFT) es un marco teórico para la construcción de la mecánica cuántica modelos de campo como sistemas o, equivalentemente, de sistemas de muchos cuerpos. Es ampliamente utilizado en la física de partículas y física de la materia condensada . La mayoría de las teorías de la física de partículas moderna, incluyendo el modelo estándar de las partículas elementales y sus interacciones, se formulan como relativistas teorías cuánticas de campos. En la física de la materia condensada, las teorías cuánticas de campo se utilizan en muchas circunstancias, especialmente aquellos en los que se permite que el número de partículas a fluctuar, por ejemplo, en el Teoría BCS de la superconductividad .
Historia
Teoría cuántica de campos se originó en el 1920 desde el problema de crear una teoría de la mecánica cuántica de la campo electromagnético. En 1926 , Max Born, Pascual Jordan, y Werner Heisenberg construido tal teoría expresando el campo de interior grados de libertad como un conjunto infinito de osciladores armónicos y empleando el procedimiento habitual para cuantificar los osciladores ( cuantización canónica). Esta teoría asume que no hay cargas eléctricas o corrientes estaban presentes y que hoy se llamaría un la teoría de campo libre. La primera teoría razonablemente completo de electrodinámica cuántica, que incluían tanto el campo electromagnético y cargadas eléctricamente cuestión (en concreto, los electrones ) como objetos de la mecánica cuántica, fue creado por Paul Dirac en 1927 . Esta teoría del campo cuántico podría ser utilizado para modelar procesos importantes tales como la emisión de un fotón por un electrón que cae en un estado cuántico de energía inferior, un proceso en el que el número de partículas cambios - un átomo en el estado inicial se convierte en un átomo además de un fotón en el estado final. Ahora se entiende que la capacidad para describir este tipo de procesos es una de las características más importantes de la teoría cuántica de campos.
Era evidente desde el principio que un tratamiento adecuado cuántica del campo electromagnético tuvo que incorporar de alguna manera de Einstein de la relatividad teoría, que después de todo había crecido a partir del estudio de electromagnetismo clásico. Esta necesidad de armar la relatividad y la mecánica cuántica fue la segunda motivación principal en el desarrollo de la teoría cuántica de campos. Pascual Jordan y Wolfgang Pauli mostró en 1928 que los campos cuánticos podrían hacer que se comporten de la manera predicha por la relatividad especial durante transformaciones de coordenadas (en concreto, demostraron que el campo conmutadores eran Lorentz invariante), y en 1933 Niels Bohr y Leon Rosenfeld mostró que este resultado puede interpretarse como una limitación de la capacidad de medir los campos en separaciones espaciales similares, tal y como lo requiere la relatividad. Un nuevo impulso para la teoría cuántica de campos vino con el descubrimiento de la Ecuación de Dirac, una ecuación de una sola partícula obedecer tanto la relatividad y la mecánica cuántica, cuando se demostró que varias de sus propiedades indeseables (tales como estados de energía negativa) podría ser eliminado por reformular la ecuación de Dirac como una teoría cuántica de campos. Este trabajo fue realizado por Wendell Furry, Robert Oppenheimer , Vladimir Fock, y otros.
El tercer hilo en el desarrollo de la teoría cuántica de campos fue la necesidad de manipular las estadísticas de los sistemas de muchas partículas consistentemente y con facilidad. En 1927 , Jordania intentó ampliar la cuantización canónica de campos para las funciones de onda de muchos cuerpos de partículas idénticas, un procedimiento que a veces se llama segunda cuantización. En 1928 , Jordania y Eugene Wigner encontró que el campo cuántico que describe los electrones, u otro fermiones, tuvieron que ser ampliado utilizando anti-desplazamientos operadores de creación y aniquilación debido a la Principio de exclusión de Pauli. Este hilo del desarrollo se incorporó en la teoría de muchos cuerpos, y fuertemente influenciados física de la materia condensada y la física nuclear .
A pesar de sus éxitos iniciales, la teoría cuántica de campos fue plagado por una serie de dificultades teóricas serias. Muchas cantidades físicas aparentemente inocuos, como el cambio de energía de estados electrónicos debido a la presencia del campo electromagnético, dieron el infinito - un resultado sin sentido - cuando calcula utilizando la teoría cuántica de campos. Este "problema de divergencia" se resolvió durante el 1940 por Ser El, Tomonaga, Schwinger, Feynman , y Dyson, a través del procedimiento conocido como renormalización . Esta fase de desarrollo culminó con la construcción de la moderna teoría de electrodinámica cuántica (QED). A partir de la 1950 con el trabajo de Yang y Mills, QED se generalizó a una clase de teorías cuánticas de campos conocidos como evaluar teorías. La 1960 y 1970 vio a la formulación de una teoría gauge ahora conocido como el Modelo Estándar de la física de partículas , que describe todas las partículas elementales conocidas y las interacciones entre ellos. La parte de interacción débil del modelo estándar fue formulado por Sheldon Glashow, con la Mecanismo de Higgs agregó por Steven Weinberg y Abdus Salam. La teoría se demostró que era coherente por Gerardus 't Hooft y Martinus Veltman.
También durante el 1970 la evolución paralela en el estudio de transiciones de fase en la física de la materia condensada llevaron Leo Kadanoff, Michael Fisher y Kenneth Wilson (extendiendo el trabajo de Ernst Stueckelberg, Andre Peterman, Murray Gell-Mann y Francis Low) a un conjunto de ideas y métodos conocido como el grupo de renormalización. Al proporcionar una mejor comprensión física del procedimiento de renormalización inventado en el 1940, el grupo de renormalización desató lo que se ha llamado el "gran síntesis" de la física teórica, uniendo las técnicas teóricas de campo cuántico utilizados en física de partículas y la física de la materia condensada en un único marco teórico.
El estudio de la teoría cuántica de campos está vivo y floreciente, al igual que las aplicaciones de este método a muchos problemas físicos. Sigue siendo una de las zonas más vitales de la física teórica actual, proporcionando un lenguaje común a muchas ramas de la física .
Principios de la teoría cuántica de campos
Campos clásicos y campos cuánticos
La mecánica cuántica , en su formulación más general, es una teoría de la abstracción operadores (observables) que actúa sobre un espacio estado abstracto ( Espacio de Hilbert), donde los observables representan cantidades físicamente observables y el espacio de estados representa los posibles estados del sistema en estudio. Además, cada observable corresponde, en un sentido técnico, a la idea clásica de una grado de libertad. Por ejemplo, los observables fundamentales asociados con el movimiento de una sola partícula de la mecánica cuántica son los operadores posición y el momento 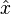 y
y 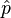 . La mecánica cuántica ordinaria se ocupa de sistemas como este, que poseen un pequeño conjunto de grados de libertad.
. La mecánica cuántica ordinaria se ocupa de sistemas como este, que poseen un pequeño conjunto de grados de libertad.
(Es importante señalar, en este punto, que este artículo no utiliza la palabra " partícula "en el contexto de la dualidad onda-partícula. En la teoría cuántica de campos, "partícula" es un término genérico para cualquier entidad mecánica cuántica discreta, tal como un electrón, que puede comportarse como partículas clásicas o las ondas clásicas bajo diferentes condiciones experimentales.)
Un campo cuántico es un sistema mecánico cuántico que contiene un gran, y posiblemente infinito , el número de grados de libertad. Esto no es tan exótica una situación como uno podría pensar. La campo clásico contiene un conjunto de grados de libertad en cada punto del espacio; Por ejemplo, la clásica campo electromagnético define dos vectores - el campo eléctrico y la campo magnético - que puede tomar, en principio, en los valores distintos para cada posición  . Cuando el campo en su conjunto se considera como un sistema mecánico cuántico, sus observables forman un infinito (de hecho conjunto no numerable), porque
. Cuando el campo en su conjunto se considera como un sistema mecánico cuántico, sus observables forman un infinito (de hecho conjunto no numerable), porque  es continua.
es continua.
Por otra parte, los grados de libertad en un campo cuántico están dispuestos en conjuntos "repetidas". Por ejemplo, los grados de libertad en un campo electromagnético pueden ser agrupados de acuerdo a la posición  , Con exactamente dos vectores para cada
, Con exactamente dos vectores para cada  . Tenga en cuenta que
. Tenga en cuenta que  es un número ordinario que "índices" los observables; no se debe confundir con el operador posición
es un número ordinario que "índices" los observables; no se debe confundir con el operador posición 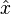 encontrado en la mecánica cuántica ordinaria, que es un observable. (Por lo tanto, la mecánica cuántica ordinaria se refieren a veces como "la teoría cuántica de campos de dimensión cero", ya que contiene sólo un único conjunto de observables.) También es importante tener en cuenta que no hay nada especial acerca de
encontrado en la mecánica cuántica ordinaria, que es un observable. (Por lo tanto, la mecánica cuántica ordinaria se refieren a veces como "la teoría cuántica de campos de dimensión cero", ya que contiene sólo un único conjunto de observables.) También es importante tener en cuenta que no hay nada especial acerca de  ya que, como resulta, en general hay más de una forma de indexación de los grados de libertad en el campo.
ya que, como resulta, en general hay más de una forma de indexación de los grados de libertad en el campo.
En las secciones siguientes, vamos a mostrar cómo estas ideas pueden ser utilizados para construir una teoría de la mecánica cuántica con las propiedades deseadas. Vamos a comenzar hablando de una sola partícula mecánica cuántica y la teoría asociada de la mecánica cuántica de muchas partículas. Luego, mediante la búsqueda de una forma de índice de los grados de libertad en el problema de muchas partículas, vamos a construir un campo cuántico y estudiar sus implicaciones.
Single-partículas y la mecánica cuántica de muchas partículas
En la mecánica cuántica ordinaria, el dependiente del tiempo Ecuación de Schrödinger que describe el movimiento de una partícula no relativista es
donde  es de la partícula de masa ,
es de la partícula de masa ,  se la aplica potencial, y
se la aplica potencial, y  denota la estado cuántico (estamos utilizando notación bra-ket).
denota la estado cuántico (estamos utilizando notación bra-ket).
Queremos considerar cómo este problema se generaliza a  partículas. Hay dos motivaciones para estudiar el problema de muchas partículas. La primera es una necesidad clara en la física de la materia condensada , donde normalmente el número de partículas está en el orden de número de Avogadro (6.0221415 x 10 23). La segunda motivación para el problema de muchas partículas surge de la física de partículas y el deseo de incorporar los efectos de la relatividad especial . Si se intenta incluir el relativista energía en reposo en la ecuación anterior, el resultado es o bien la Ecuación de Klein-Gordon o la Ecuación de Dirac. Sin embargo, estas ecuaciones tienen muchas cualidades insatisfactorios; por ejemplo, poseen energía valores propios que se extienden a -∞, por lo que no parece haber una definición sencilla de un estado fundamental. Resulta que estas inconsistencias se deben a dejar de lado la posibilidad de crear dinámicamente o destruir las partículas, que es un aspecto crucial de la relatividad. Einstein famoso relación masa-energía predice que las partículas suficientemente masivas pueden decaer en varias partículas más ligeras, y suficientemente partículas energéticas pueden combinarse para formar partículas masivas. Por ejemplo, un electrón y un positrones pueden aniquilarse entre sí para crear fotones . Por lo tanto, una teoría cuántica relativista consistente debe ser formulado como una teoría de muchas partículas.
partículas. Hay dos motivaciones para estudiar el problema de muchas partículas. La primera es una necesidad clara en la física de la materia condensada , donde normalmente el número de partículas está en el orden de número de Avogadro (6.0221415 x 10 23). La segunda motivación para el problema de muchas partículas surge de la física de partículas y el deseo de incorporar los efectos de la relatividad especial . Si se intenta incluir el relativista energía en reposo en la ecuación anterior, el resultado es o bien la Ecuación de Klein-Gordon o la Ecuación de Dirac. Sin embargo, estas ecuaciones tienen muchas cualidades insatisfactorios; por ejemplo, poseen energía valores propios que se extienden a -∞, por lo que no parece haber una definición sencilla de un estado fundamental. Resulta que estas inconsistencias se deben a dejar de lado la posibilidad de crear dinámicamente o destruir las partículas, que es un aspecto crucial de la relatividad. Einstein famoso relación masa-energía predice que las partículas suficientemente masivas pueden decaer en varias partículas más ligeras, y suficientemente partículas energéticas pueden combinarse para formar partículas masivas. Por ejemplo, un electrón y un positrones pueden aniquilarse entre sí para crear fotones . Por lo tanto, una teoría cuántica relativista consistente debe ser formulado como una teoría de muchas partículas.
Además, vamos a suponer que la  partículas son indistinguibles. Como se describe en el artículo sobre partículas idénticas, esto implica que el estado de todo el sistema debe ser simétrico ( bosones) o antisimétrica ( fermiones) cuando se intercambian las coordenadas de sus partículas constituyentes. Estos estados multi-partículas son bastante complicados de escribir. Por ejemplo, el estado cuántico general de un sistema de
partículas son indistinguibles. Como se describe en el artículo sobre partículas idénticas, esto implica que el estado de todo el sistema debe ser simétrico ( bosones) o antisimétrica ( fermiones) cuando se intercambian las coordenadas de sus partículas constituyentes. Estos estados multi-partículas son bastante complicados de escribir. Por ejemplo, el estado cuántico general de un sistema de  bosones se escribe como
bosones se escribe como
donde 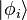 son los estados de partícula simple,
son los estados de partícula simple,  es el número de partículas que ocupan estado
es el número de partículas que ocupan estado  , Y la suma se toma sobre todos los posibles permutaciones
, Y la suma se toma sobre todos los posibles permutaciones  actuando
actuando  elementos. En general, esta es una suma de
elementos. En general, esta es una suma de 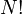 (
(  factorial ) términos distintos, que rápidamente se convierte en inmanejable como
factorial ) términos distintos, que rápidamente se convierte en inmanejable como  aumenta. La manera de simplificar este problema es convertirlo en una teoría cuántica de campos.
aumenta. La manera de simplificar este problema es convertirlo en una teoría cuántica de campos.
Segunda cuantización
En esta sección, describiremos un método para construir una teoría del campo cuántico llamado segunda cuantización. Esto, básicamente, consiste en elegir una forma de índice de los grados de la mecánica cuántica de la libertad en el espacio de múltiples estados idénticos de partículas. Se basa en el Formulación hamiltoniana de la mecánica cuántica; existen varios otros enfoques, tales como la Camino de Feynman integral, que utiliza una Formulación de Lagrange. Para una visión general, ver el artículo sobre cuantización.
Segunda cuantización de bosones
Para simplificar, vamos a discutir primero segundo cuantificación para bosones, que forman estados cuánticos perfectamente simétricas. Denotemos los estados de partícula simple mutuamente ortogonales por 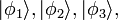 etcétera. Por ejemplo, el estado 3-partícula con una partícula en el estado de
etcétera. Por ejemplo, el estado 3-partícula con una partícula en el estado de 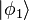 y dos en el estado de
y dos en el estado de 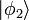 es
es
El primer paso en la segunda cuantización es expresar esos estados cuánticos en términos de números de ocupación, haciendo una lista de la cantidad de partículas que ocupan cada uno de los estados de partícula simple 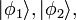 etc. Esta es simplemente otra manera de etiquetar los estados. Por ejemplo, el estado 3 de partículas anterior se denota como
etc. Esta es simplemente otra manera de etiquetar los estados. Por ejemplo, el estado 3 de partículas anterior se denota como
El siguiente paso es ampliar la  espacio de estado partícula a incluir los espacios de estado para todos los valores posibles de
espacio de estado partícula a incluir los espacios de estado para todos los valores posibles de  . Este espacio estado extendido, conocido como Espacio de Fock, se compone del espacio de estado de un sistema sin partículas (el llamado estado de vacío), más el espacio de estado de un sistema de 1-partícula, más el espacio de estado de un sistema de 2-partículas, y así sucesivamente. Es fácil ver que hay una correspondencia uno a uno entre la representación número de ocupación y estados bosón válidos en el espacio de Fock.
. Este espacio estado extendido, conocido como Espacio de Fock, se compone del espacio de estado de un sistema sin partículas (el llamado estado de vacío), más el espacio de estado de un sistema de 1-partícula, más el espacio de estado de un sistema de 2-partículas, y así sucesivamente. Es fácil ver que hay una correspondencia uno a uno entre la representación número de ocupación y estados bosón válidos en el espacio de Fock.
En este punto, el sistema mecánico cuántico se ha convertido en un campo cuántico en el sentido que se describe anteriormente. Grados de primaria de la esfera de la libertad son los números de ocupación, y cada número de ocupación se indexa por un número 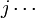 , Lo que indica que de los estados de partícula simple
, Lo que indica que de los estados de partícula simple 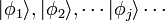 se refiere a.
se refiere a.
Las propiedades de este campo cuántico se pueden explorar mediante la definición operadores de creación y aniquilación, que añaden partículas y restar. Son análogos a los "operadores de escalera" en la cuántica problema oscilador armónico, lo que sumado y restado cuantos de energía. Sin embargo, estos operadores, literalmente, crean y aniquilan partículas de un estado cuántico dado. El operador de aniquilación bosonic 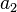 y el operador de la creación
y el operador de la creación 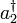 tener los siguientes efectos:
tener los siguientes efectos:
Se puede demostrar que estos son los operadores en el sentido habitual de la mecánica cuántica, es decir, operadores lineales que actúan sobre el espacio de Fock. Además, son de hecho Conjugados hermitianas, lo que justifica la forma en que ellos han escrito. Se puede demostrar que obedecer la relación de conmutación
donde  representa el Delta Kronecker. Estas son precisamente las relaciones obedecidas por los operadores de escalera para un conjunto infinito de independiente osciladores armónicos cuánticos, uno para cada estado de una sola partícula. Adición o eliminación de los bosones de cada estado es, por tanto, análogo al emocionante o de-excitación de un cuanto de energía en un oscilador armónico.
representa el Delta Kronecker. Estas son precisamente las relaciones obedecidas por los operadores de escalera para un conjunto infinito de independiente osciladores armónicos cuánticos, uno para cada estado de una sola partícula. Adición o eliminación de los bosones de cada estado es, por tanto, análogo al emocionante o de-excitación de un cuanto de energía en un oscilador armónico.
La Hamiltoniano del campo cuántico (que, a través de la Ecuación de Schrödinger, determina su dinámica) se puede escribir en términos de los operadores de creación y aniquilación. Por ejemplo, el hamiltoniano de un campo de (sin interacción) bosones libres es
donde  es la energía de la
es la energía de la  -ésimo estado propio de energía de una sola partícula. Tenga en cuenta que
-ésimo estado propio de energía de una sola partícula. Tenga en cuenta que
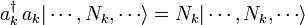 .
.
Segunda cuantización de fermiones
Resulta que una definición diferente de la creación y la aniquilación debe ser utilizado para describir fermiones. De acuerdo con la Principio de exclusión de Pauli, fermiones no puede compartir estados cuánticos, por lo que sus números de ocupación  sólo puede tomar el valor 0 ó 1. Los operadores de aniquilación fermionic
sólo puede tomar el valor 0 ó 1. Los operadores de aniquilación fermionic  y operadores de creación
y operadores de creación  se definen por
se definen por
Estos obedecen a una relación anticonmutación:
Uno puede notar de ello que la aplicación de un operador de creación fermiónica dos veces da cero, por lo que es imposible que las partículas de compartir estados de partícula simple, de conformidad con el principio de exclusión.
Los operadores de campo
Hemos mencionado anteriormente que no puede haber más de una forma de indexación de los grados de libertad en un campo cuántico. Índices de cuantificación Segundas el campo por la enumeración de los estados cuánticos de partículas único. Sin embargo, como hemos visto, es más natural pensar en un "campo", como el campo electromagnético, como un conjunto de grados de libertad en un índice por la posición.
Para este fin, podemos definir los operadores de campo que crean o destruyen una partícula en un punto particular en el espacio. En la física de partículas, estos operadores resultan ser más conveniente para trabajar, ya que hacen más fácil formular teorías que satisfagan las demandas de la relatividad.
Estados Single-partículas se enumeran generalmente en términos de su momentos (como en el partícula en un problema de la caja.) Podemos construir los operadores de campo mediante la aplicación de la Transformada de Fourier a los operadores de creación y aniquilación de estos estados. Por ejemplo, el operador de campo aniquilación bosonic 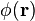 es
es
Los operadores de campo bosónicos obedecen a la relación de conmutación
donde 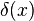 representa el Función delta de Dirac. Como antes, las relaciones fermiónicos son los mismos, con los conmutadores reemplazados por anticommutators.
representa el Función delta de Dirac. Como antes, las relaciones fermiónicos son los mismos, con los conmutadores reemplazados por anticommutators.
Cabe destacar que el operador de campo no es lo mismo que una función de onda-partícula. El primero es un operador que actúa sobre el espacio de Fock, y el último es sólo un campo escalar. Sin embargo, están estrechamente relacionados, y de hecho son comúnmente denotan con el mismo símbolo. Si tenemos un hamiltoniano con una representación del espacio, dicen
donde los índices  y
y  atropellar a todas las partículas, el hamiltoniano teoría de campo es
atropellar a todas las partículas, el hamiltoniano teoría de campo es
Esto se parece mucho a una expresión para el valor esperado de la energía, con  interpretando el papel de la función de onda. Esta relación entre los operadores de campo y funciones de onda hace que sea muy fácil de formular teorías de campo a partir de hamiltonianos espacio proyectado.
interpretando el papel de la función de onda. Esta relación entre los operadores de campo y funciones de onda hace que sea muy fácil de formular teorías de campo a partir de hamiltonianos espacio proyectado.
Implicaciones de la teoría cuántica de campos
Unificación de campos y partículas
El procedimiento de "segunda cuantización" que hemos descrito en el apartado anterior toma un conjunto de estados cuánticos de partículas solo como punto de partida. A veces, es imposible definir tales estados de partícula simple, y hay que proceder directamente a la teoría cuántica de campos. Por ejemplo, una teoría cuántica de la campo electromagnético debe ser una teoría cuántica de campos, porque es imposible (por diversas razones) para definir un función de onda para un solo fotón . En tales situaciones, la teoría cuántica de campos se puede construir mediante el examen de las propiedades mecánicas del campo clásico y adivinar el correspondiente teoría cuántica. Las teorías cuánticas de campos obtenidos de este modo tienen las mismas propiedades que los obtenidos utilizando segunda cuantización, como la creación como bien definida y operadores de aniquilación que obedecen conmutación o anticonmutación relaciones.
La teoría cuántica de campos proporciona un marco unificado para la descripción de objetos "de campo como" (como el campo electromagnético, cuya excitaciones son fotones) y objetos "similares a las partículas" (como los electrones, que son tratados como excitaciones de un campo de electrones subyacente ).
Significado físico de partículas indistinguibilidad
El segundo procedimiento de cuantificación depende crucialmente de las partículas que son idéntica. Lo que no habría sido capaz de construir una teoría cuántica de campos de un sistema de muchas partículas distinguibles, porque no habría habido forma de separar y la indexación de los grados de libertad.
Muchos físicos prefieren tomar la interpretación inversa, que es que la teoría cuántica de campos se explica qué son partículas idénticas. En la mecánica cuántica ordinaria, no hay mucha motivación teórica para el uso simétrico (bosonic) o antisimétricos estados (fermionic), y la necesidad de esos estados es simplemente considerado como un hecho empírico. Desde el punto de vista de la teoría cuántica de campos, las partículas son idénticos si y sólo si son excitaciones del mismo campo cuántico subyacente. Por lo tanto, la pregunta "¿por qué todos los electrones idénticos?" surge de error con respecto a los electrones individuales como objetos fundamentales, cuando en realidad es sólo el campo de electrones que es fundamental.
La conservación de las partículas y no conservación
Durante la segunda cuantización, empezamos con un espacio de Hamilton y el estado que describe un número fijo de partículas (  ), Y terminó con un hamiltoniano y espacio de estados para un número arbitrario de partículas. Por supuesto, en muchas situaciones comunes
), Y terminó con un hamiltoniano y espacio de estados para un número arbitrario de partículas. Por supuesto, en muchas situaciones comunes  es una cantidad importante y perfectamente bien definida, por ejemplo, si estamos describiendo un gas de átomos sellados en una caja. Desde el punto de vista de la teoría cuántica de campos, tales situaciones son descritas por los estados cuánticos que son estados propios de la operador número
es una cantidad importante y perfectamente bien definida, por ejemplo, si estamos describiendo un gas de átomos sellados en una caja. Desde el punto de vista de la teoría cuántica de campos, tales situaciones son descritas por los estados cuánticos que son estados propios de la operador número 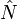 , Que mide el número total de partículas presentes. Como con cualquier cuántico observable mecánica,
, Que mide el número total de partículas presentes. Como con cualquier cuántico observable mecánica, 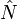 es conservada si conmuta con el hamiltoniano. En ese caso, el estado cuántico está atrapado en el
es conservada si conmuta con el hamiltoniano. En ese caso, el estado cuántico está atrapado en el  partícula a subespacio del espacio de Fock total y la situación podría igualmente ser descrito por ordinario
partícula a subespacio del espacio de Fock total y la situación podría igualmente ser descrito por ordinario  la mecánica cuántica partícula a.
la mecánica cuántica partícula a.
Por ejemplo, podemos ver que el hamiltoniano libre de Higgs se ha descrito anteriormente conserva el número de partículas. Cada vez que el hamiltoniano opera en un estado, cada partícula destruida por un operador de aniquilación 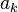 es inmediatamente puesto de nuevo por el operador de la creación
es inmediatamente puesto de nuevo por el operador de la creación 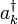 .
.
Por otro lado, es posible, y de hecho común, encontrar estados cuánticos que no son estados propios de 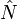 , Que no tienen número de partículas bien definidas. Dichos estados son difíciles o imposibles de manejar utilizando la mecánica cuántica ordinaria, pero que se pueden describir fácilmente en la teoría cuántica de campos como superposiciones cuánticas de estados que tienen diferentes valores de
, Que no tienen número de partículas bien definidas. Dichos estados son difíciles o imposibles de manejar utilizando la mecánica cuántica ordinaria, pero que se pueden describir fácilmente en la teoría cuántica de campos como superposiciones cuánticas de estados que tienen diferentes valores de  . Por ejemplo, supongamos que tenemos un campo bosonic cuyas partículas pueden ser creados o destruidos por las interacciones con un campo fermiónica. El hamiltoniano del sistema combinado estaría dada por los hamiltonianos del bosón libre y campos de fermiones gratuitos, además de una "energía potencial" término como
. Por ejemplo, supongamos que tenemos un campo bosonic cuyas partículas pueden ser creados o destruidos por las interacciones con un campo fermiónica. El hamiltoniano del sistema combinado estaría dada por los hamiltonianos del bosón libre y campos de fermiones gratuitos, además de una "energía potencial" término como
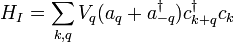 ,
,
donde 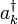 y
y 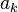 denota los operadores de creación y aniquilación bosónicos,
denota los operadores de creación y aniquilación bosónicos, 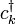 y
y  denota los operadores de creación y aniquilación fermionic, y
denota los operadores de creación y aniquilación fermionic, y 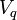 es un parámetro que describe la fuerza de la interacción. Esta "interacción plazo" describe los procesos en los que un fermión en el estado
es un parámetro que describe la fuerza de la interacción. Esta "interacción plazo" describe los procesos en los que un fermión en el estado  o bien absorbe o emite un bosón, por lo tanto ser pateado en un estado propio diferente
o bien absorbe o emite un bosón, por lo tanto ser pateado en un estado propio diferente 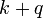 . (De hecho, este tipo de hamiltoniano se utiliza para describir la interacción entre electrones de conducción y fonones en metales . La interacción entre los electrones y los fotones se trata de una manera similar, pero es un poco más complicada porque el papel de giro debe ser tenido en cuenta.) Una cosa a notar aquí es que incluso si comenzamos con un número fijo de bosones, por lo general a terminar con una superposición de estados con diferente número de bosones en tiempos posteriores. El número de fermiones, sin embargo, se conserva en este caso.
. (De hecho, este tipo de hamiltoniano se utiliza para describir la interacción entre electrones de conducción y fonones en metales . La interacción entre los electrones y los fotones se trata de una manera similar, pero es un poco más complicada porque el papel de giro debe ser tenido en cuenta.) Una cosa a notar aquí es que incluso si comenzamos con un número fijo de bosones, por lo general a terminar con una superposición de estados con diferente número de bosones en tiempos posteriores. El número de fermiones, sin embargo, se conserva en este caso.
En la física de la materia condensada , los estados con el número de partículas mal definidos son particularmente importantes para la descripción de los distintos superfluidos. Muchas de las características definitorias de un superfluido surgen de la noción de que su estado cuántico es una superposición de estados con diferentes números de partículas.
Enfoques axiomáticos
La descripción precedente de la teoría cuántica de campos sigue el espíritu con el que más los físicos abordan el tema. Sin embargo, no es matemáticamente riguroso. Durante las últimas décadas, ha habido muchos intentos de poner la teoría cuántica de campos en una base matemática firme mediante la formulación de un conjunto de axiomas para él. Estos intentos se dividen en dos amplias clases.
La primera clase de axiomas, propuso por primera vez durante el 1950, incluya el Wightman, Osterwalder-Schrader, y Sistemas Haag-Kastler. Ellos intentaron formalizar noción de un "campo de operador con valores" de los físicos en el contexto de análisis funcional, y un éxito limitado disfrutado. Se pudo demostrar que cualquier teoría cuántica de campos satisfacer estos axiomas satisfecho ciertos teoremas generales, tales como la spin-estadísticas teorema y la Teorema CPT. Por desgracia, resultó extraordinariamente difícil demostrar que cualquier teoría del campo realista, incluyendo el Modelo Estándar , satisfecho estos axiomas. La mayoría de las teorías que podrían ser tratados con estos axiomas analíticas eran físicamente trivial, está restringido a bajas dimensiones y que carecen de dinámicas interesantes. La construcción de las teorías que satisfacen uno de estos conjuntos de axiomas cae en el campo de la la teoría cuántica de campos constructiva. Un trabajo importante fue hecho en esta área en el 1970 por Segal, Glimm, Jaffe y otros.
Durante el 1980, un segundo conjunto de axiomas basados en geométricas las ideas se propuso. Esta línea de investigación, lo que restringe su atención a una clase particular de las teorías cuánticas de campos conocidos como teorías cuánticas de campos topológicas, se asocia más estrechamente con Michael Atiyah y Graeme Segal, y fue sobre todo siempre completada por Edward Witten, Richard Borcherds, y Maxim Kontsevich. Sin embargo, las teorías cuánticas de campos físicamente más relevantes, como el modelo estándar , no son teorías cuánticas de campos topológicas; la teoría cuántica de campos de la Efecto Hall cuántico fraccionario es una excepción notable. El principal impacto de la teoría axiomática campo cuántico topológico ha estado en matemáticas, con importantes aplicaciones en teoría de la representación, topología algebraica y la geometría diferencial .
Encontrar los axiomas adecuados para la teoría cuántica de campos es aún un problema abierto y difícil en las matemáticas. Uno de los Problemas del milenio-prueba de la existencia de un brecha masiva en Yang-Mills teoría está relacionada con este tema.
Fenómenos asociados a la teoría cuántica de campos
En la parte anterior del artículo, describimos las propiedades más generales de las teorías cuánticas de campos. Algunas de las teorías cuánticas de campos estudiados en diversos campos de la física teórica poseen propiedades especiales adicionales, como renormalizabilidad, simetría gauge, y la supersimetría. Estos se describen en las siguientes secciones.
Renormalización
Al principio de la historia de la teoría cuántica de campos, se encontró que muchos cálculos aparentemente inocuos, como el perturbative cambio en la energía de un electrón debido a la presencia del campo electromagnético, da resultados infinitos. Muchos de estos problemas están relacionados con fallas en electrodinámica clásica que fueron identificados (pero sin resolver) que se remontan a la del siglo 19 , y que básicamente se derivan del hecho de que muchas de las propiedades supuestamente "intrínsecas" de un electrón están vinculados al campo electromagnético con el que interactúa. Para ilustrar esto, el recuerdo de la discusión anterior que el hamiltoniano de interacción entre dos campos cuánticos, como el campo de electrones y el campo electromagnético, no es necesario conservar el número de partículas. Por lo tanto, incluso si empezamos con un solo electrón y no hay fotones, el estado cuántico evolucionará rápidamente en una superposición de estados que pueden incluir uno o más fotones. Por lo tanto, la energía transportada por que "solo" electrón-su auto no energético es simplemente el valor "desnudo", sino que también incluye la energía contenida en una nube asistente de fotones. Cuando se calcula esta energía auto, se encuentra que la contribución de los fotones que posee arbitrariamente altas energías (o, equivalentemente, arbitrariamente corto longitudes de onda) conduce a un valor infinito formalmente.
La solución a este problema, primero dada por Julian Schwinger, se llama renormalización . La idea es imponer un " punto de corte "para la contribución fotónico, por ejemplo, al postular que los fotones no pueden poseer energías por encima de algún valor extremadamente alto. Cualquier cantidad que deseamos calcular, tales como la energía en reposo, ahora es finito, pero depende de la de corte. A continuación, refundición el resultado en términos cantidades de físicamente observables, tales como la masa del electrón observada, en lugar de cantidades observables, tales como la energía de corte y la masa del electrón desnudo. El resultado final es independiente de todos los detalles del procedimiento de corte, incluyendo el valor de la energía de corte, siempre que la procesos relevantes ocurren a energías muy por debajo del punto de corte.
El procedimiento de renormalización sólo funciona para una determinada clase de teorías cuánticas de campo, llamado teorías cuánticas de campos renormalizables. El Modelo Estándar de la física de partículas es renormalizable, y también lo son sus teorías componentes ( electrodinámica cuántica / teoría electrodébil y cromodinámica cuántica). Según la teoría de la grupo de renormalización, cada teoría renormalizable un límite de baja energía única (es decir, la llamada un " teoría efectiva campo ") para una amplia gama de las teorías de alta energía. renormalizable teorías son, por tanto, independiente de la naturaleza precisa de los fenómenos de alta energía subyacentes.
Libertad Gauge
La Teoría Gauge es una teoría que admite un simetría con un parámetro local. Por ejemplo, en cada cuántica teoría del mundial fase de la función de onda es arbitraria y no representa algo físico. En consecuencia, la teoría es invariante bajo un cambio global de las fases (agregar una constante a la fase de todas las funciones de onda, en todas partes); esto es un simetría global. En electrodinámica cuántica, la teoría también es invariante bajo un cambio local de fase, es decir - se puede desplazar la fase de todos funciones de onda de modo que el cambio puede ser diferente en cada punto espacio tiempo. Esto es un simetría local. Sin embargo, para que un bien definido derivado operador de que exista, se debe introducir un nuevo campo, el campo de calibre, que también se transforma para que el cambio local de variables (la fase en nuestro ejemplo) para no afectar el derivado. En electrodinámica cuántica este campo de norma es el campo electromagnético. La ruptura de carga locales de variables se denomina medir transformación.
En la teoría cuántica de campos las excitaciones de campos representan partículas. La partícula asociada con excitaciones de la campo de norma es el Higgs calibre, que es el de fotones en el caso de electrodinámica cuántica.
La grados de libertad en la teoría cuántica de campos son fluctuaciones locales de los campos. La existencia de una simetría gauge reduce el número de grados de libertad, simplemente porque algunas fluctuaciones de los campos pueden ser transformados a cero medir las transformaciones, por lo que son equivalentes a no tener fluctuaciones en absoluto, y por lo tanto no tienen ningún significado físico. Estas fluctuaciones son generalmente llamados "grados no físicos de la libertad" o artefactos calibre; por lo general algunos de ellos tienen un negativo norma, haciéndolos inadecuados para una teoría consistente. Por lo tanto, si una teoría de campo clásica tiene una simetría gauge, entonces su versión cuantificada (es decir, la teoría cuántica de campos correspondientes) tendrá esta simetría también. En otras palabras, una simetría de calibre no puede tener un quantum anomalía. Si una simetría gauge es anómala (es decir, no se mantiene en la teoría cuántica) entonces la teoría no es consistente: por ejemplo, en la electrodinámica cuántica, había habido un medidor de anomalía, esto requeriría la aparición de fotones con longitudinal polarización y polarización en el tiempo dirección, siempre que éste, un negativo norma, lo que hace la teoría inconsistente; otra posibilidad sería que estos fotones que aparezcan sólo en procesos intermedios, pero no en los productos finales de cualquier interacción, haciendo que la teoría no unitario y de nuevo inconsistente (ver teorema óptico).
En general, la transformaciones gauge de una teoría constan varias transformaciones diferentes, que pueden no ser conmutativa . Estas transformaciones están juntos descritos por un objeto matemático conocido como un grupo de calibre. infinitesimales transformaciones gauge son el grupo gauge generadores. Por lo tanto el número de bosones gauge es el grupo dimensión (es decir, número de generadores que forman una base).
Todos interacciones fundamentales de la naturaleza son descritos por evaluar teorías. Estos son:
- La electrodinámica cuántica, cuyoscalibre transformación es un cambio local de la fase, por lo que elgrupo de gauge esU (1). La bosón gauge es elfotón.
- Cromodinámica cuántica, cuyoindicador de grupo es SU (3). La bosones gauge son ocho gluones.
- La Teoría electrodébil, cuyogrupo de calibre es
 (A producto directo de laU (1) ySU (2)).
(A producto directo de laU (1) ySU (2)). - La gravedad, cuya teoría clásica esla relatividad general, admite el principio de equivalencia, que es una forma de simetría gauge.
La supersimetría
La supersimetría asume que cada fundamental fermión tiene una supercompañera que es un bosón y viceversa. Fue introducido con el fin de resolver el llamado problema de jerarquía, es decir, para explicar por qué las partículas no protegidos por cualquier simetría (como el bosón de Higgs) no reciben correcciones radiativas a su masa de conducir a las escalas mayores (GUT, Planck ...). Pronto se dio cuenta de que la supersimetría tiene otras propiedades interesantes: su versión calibrada es una extensión de la relatividad general ( supergravedad), y es un ingrediente clave para la consistencia de la teoría de cuerdas .
La supersimetría manera protege las jerarquías es la siguiente: puesto que para cada partícula hay un supercompañera con la misma masa, cualquier bucle en una corrección radiativo es cancelada por el bucle correspondiente a su supercompañera, haciendo que la teoría finita UV.
Dado que todavía no se han observado supercompañeros, si existe supersimetría debe ser rota (a través de un denominado término suave, que rompe la supersimetría sin arruinar sus características útiles). Los modelos más simples de esta última hora requieren que la energía de los supercompañeros no sea demasiado alta; en estos casos, se espera que la supersimetría para ser observado por experimentos en el Gran Colisionador de Hadrones.
![\ Left [\ frac {| \ mathbf {p} | ^ 2} {2m} + V (\ mathbf {r}) \ right] | \ psi (t) \ rang = i \ hbar \ frac {\ partial} { \ t parcial} | \ psi (t) \ rang,](../../images/261/26195.png)
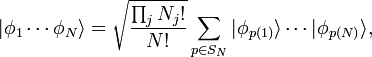
![\ Frac {1} {\ sqrt {3}} \ left [| \ phi_1 \ rang | \ phi_2 \ rang | \ phi_2 \ rang + | \ phi_2 \ rang | \ phi_1 \ rang | \ phi_2 \ rang + | \ phi_2 \ rang | \ phi_2 \ rang | \ phi_1 \ rang \ right].](../../images/262/26203.png)

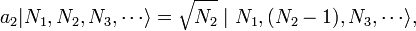
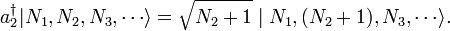
![\ Left [a_i, A_j \ right] = 0 \ quad \ quad \ left [a_i ^ \ daga, A_j ^ \ daga \ right] = 0 \ quad \ quad \ left [a_i, A_j ^ \ daga \ right] = \ delta_ {ij},](../../images/262/26211.png)
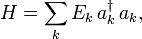
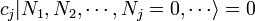
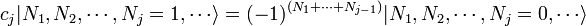
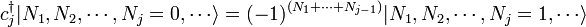
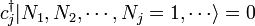

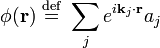
![\ Left [\ phi (\ mathbf {r}), \ phi (\ mathbf {r '}) \ right] = 0 \ quad \ quad \ left [\ phi ^ \ daga (\ mathbf {r}), \ phi ^ \ daga (\ mathbf {r '}) \ right] = 0 \ quad \ quad \ left [\ phi (\ mathbf {r}), \ phi ^ \ daga (\ mathbf {r'}) \ right ] = \ delta ^ 3 (\ mathbf {r} - \ mathbf {r '})](../../images/262/26222.png)