
Impulso
Antecedentes
SOS Children, que corre cerca de 200 sos escuelas en el mundo en desarrollo, organizó esta selección. El patrocinio de los niños ayuda a los niños en el mundo en desarrollo para aprender también.
| La mecánica clásica |
|---|
|
Ramas
|
Formulaciones Mecánica analítica ( Mecánica lagrangiana Mecánica hamiltoniana) |
Conceptos fundamentales
|
Temas básicos Cuerpo rígido
Ley de Newton gravitación universal
Inercial / No inercial marco de referencia
Mecánica de planar movimiento de las partículas
|
El movimiento de rotación Movimiento circular
Fuerza centrífuga
|

En la mecánica clásica , el impulso ( pl. momentos; SI unidad kg · m / s, o, equivalentemente, N · s) es el producto de la masa y la velocidad de un objeto (p = mv). Para las medidas más precisas de impulso, consulte la sección "definiciones modernas de impulso" en esta página. Se refiere a veces como el impulso lineal para distinguirlo del tema conexo de momento angular . Momento lineal es una cantidad vectorial, ya que tiene una dirección, así como una magnitud. El momento angular es una cantidad pseudovector porque gana un flip signo adicional en virtud de un la rotación inadecuada el momento total de ningún grupo de objetos sigue siendo el mismo a menos que las fuerzas exteriores actúan sobre el objeto.
Momentum es un cantidad conservada, lo que significa que el momento total de cualquier sistema cerrado (uno no se ve afectado por fuerzas externas) no puede cambiar.
Historia del concepto
La palabra y el concepto general de Momentum se utilizó en el República Romana principalmente en el sentido de "un movimiento, el movimiento (como una fuerza que mora ...)." Un pez fue capaz de cambiar de velocidad (Velocitas) a través del impulso de su cola. La palabra está formada por una acumulación de basta en el tallo de América Movere, "mover". Un movi-hombres- es el resultado de la Movere tan frag-men- es el resultado de frangere, "romper". Extensión por -a- obtiene mōvimentum y fragmentum, el ex contratación de impulso.
El momento no era más que la moción, que fue Motus, pero era el poder que reside en un objeto en movimiento, capturado por definiciones matemáticas de hoy. Un Motus, "movimiento", fue una etapa en cualquier tipo de cambio, mientras que Velocitas, "rapidez", capturado sólo velocidad. Los romanos, debido a las limitaciones inherentes al número romano sistema, fueron incapaces de ir más allá con la percepción.
La llegada de los números árabes en el siglo 10 abrió la puerta a la filosofía cuantitativa moderna. El concepto de impulso en la mecánica clásica se originó por una serie de grandes pensadores y experimentadores. El primero de ellos fue Ibn Sina (Avicena) circa 1000, quien se refirió a como impulso proporcional a veces el peso de velocidad . René Descartes refirió posteriormente a la masa por la velocidad como la fuerza fundamental del movimiento. Galileo en su Dos nuevas ciencias utilizan el italiano palabra "impeto."
La cuestión ha sido muy debatida en cuanto a lo que Sir Isaac Newton fue la contribución 's al concepto. Aparentemente nada, salvo para indicar con más detalle y con mejores fórmulas matemáticas lo que ya se sabe. La primera y segunda de las leyes del movimiento de Newton ya había sido declarado por John Wallis en su obra de 1670, Mechanica sive De Motu, Tractatus geometricus: "el estado inicial del cuerpo, ya sea de reposo o de movimiento, persistirán" y "Si la fuerza es mayor que la resistencia, dará como resultado el movimiento ... . "Wallis utiliza impulso y frente a la fuerza.
De Newton "Principios matemáticos de la historia natural" cuando salió por primera vez en 1686 mostró un casting similar alrededor de las palabras a utilizar para el impulso matemático. Sus define Definición II quantitas motus, "cantidad de movimiento", como "derivado de la velocidad y la cantidad de materia conjuntamente", que lo identifica como impulso. Así, cuando en la Ley II se refiere a mutatio motus "cambio de movimiento", es proporcional a la fuerza aplicada, que se toma generalmente para significar el impulso y no movimiento.
Sólo faltaba para asignar un término estándar para la cantidad de movimiento. El primer uso de "impulso" en su sentido matemático adecuado no es clara, pero por el momento de la Miscelánea de Jenning en 1721, cuatro años antes de la edición final de Principia Mathematica de Newton, el momento M o "cantidad de movimiento" se está definiendo para los estudiantes como "un rectángulo", el producto de Q y V, donde Q es "cantidad de material" y V es "velocidad", s / t.
Momento lineal de una partícula
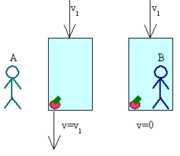
Si un objeto se está moviendo en cualquier marco de referencia, entonces tiene impulso en ese marco. Es importante tener en cuenta que el impulso es enmarcar dependiente. Es decir, el mismo objeto puede tener un cierto impulso en un marco de referencia, pero una cantidad diferente en otro marco. Por ejemplo, un objeto en movimiento tiene un momento en un marco de referencia fijado a un punto en el suelo, mientras que al mismo tiempo tiene 0 impulso en un marco de referencia unido al del objeto centro de masa .
La cantidad de impulso que tiene un objeto depende de dos magnitudes físicas: la masa y la velocidad del objeto en movimiento en el marco de referencia. En la física, el símbolo habitual para el impulso es un pequeño p negrita (negrita porque es un vector ); por lo que este se puede escribir:
donde:
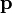 es el momento
es el momento 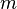 es la masa
es la masa  la velocidad
la velocidad
Ejemplo: un modelo de avión de 1 kg que viajan hacia el norte a 1 m / s en vuelo recto y nivelado tiene un impulso de 1 kg m / s derecho al norte, medida desde el suelo. Para el modelo de piloto en la cabina que tiene una velocidad y el impulso de cero.
De acuerdo con la segunda ley de Newton de la tasa de variación del momento de una partícula es proporcional a la fuerza resultante que actúa sobre la partícula y es en la dirección de esa fuerza. En el caso de masa constante, y las velocidades mucho menores que la velocidad de la luz, esta definición los resultados en la ecuación
o simplemente
donde se entiende F ser el resultante .
Ejemplo: un modelo de avión de 1 kg acelera desde el reposo hasta una velocidad de 1 m / s hacia el norte en 1 seg. El empuje necesario para producir esta aceleración es 1 newton. El cambio en el momento es 1 kg-m / seg. Para el modelo de piloto en la cabina no hay un cambio de impulso. Su presionando hacia atrás en el asiento es una reacción al empuje desequilibrado, que pronto será equilibrada por el arrastre.
Momento lineal de un sistema de partículas
En relación a la masa y la velocidad
El momento lineal de un sistema de partículas es la suma vectorial de los momentos de todos los objetos individuales en el sistema.
donde
 es el impulso del sistema de partículas
es el impulso del sistema de partículas 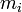 es la masa del objeto i
es la masa del objeto i  el vector de velocidad del objeto i
el vector de velocidad del objeto i 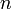 es el número de objetos en el sistema de
es el número de objetos en el sistema de
Se puede demostrar que, en el el centro del marco de masas el impulso de un sistema es cero. Además, el impulso en un marco de referencia que se mueve a una velocidad  con respecto a ese fotograma es simplemente:
con respecto a ese fotograma es simplemente:
donde:
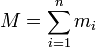 .
.
En relación con fuerza- ecuaciones generales del movimiento
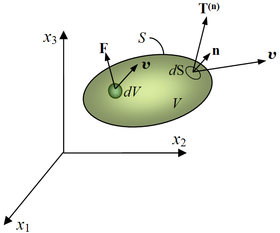
El momento lineal de un sistema de partículas también se puede definir como el producto de la masa total  del sistema de veces la velocidad del centro de masa
del sistema de veces la velocidad del centro de masa 
Esto se conoce comúnmente como la segunda ley de Newton .
Para una derivación más general mediante tensores, consideramos un cuerpo en movimiento (ver figura), asumimos como continuum, que ocupa un volumen  en un momento
en un momento  , Tiene un área superficial
, Tiene un área superficial 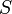 , Con las fuerzas de tracción o de superficie definidos
, Con las fuerzas de tracción o de superficie definidos  que actúan sobre cada punto de la superficie del cuerpo, fuerzas de cuerpo
que actúan sobre cada punto de la superficie del cuerpo, fuerzas de cuerpo  por unidad de volumen en cada punto dentro del volumen
por unidad de volumen en cada punto dentro del volumen  Y un campo de velocidad
Y un campo de velocidad  prescrita por todo el cuerpo. Después de la ecuación anterior, la cantidad de movimiento del sistema es:
prescrita por todo el cuerpo. Después de la ecuación anterior, la cantidad de movimiento del sistema es:
Por definición, el estrés vector es  , A continuación,
, A continuación,
Usando el Teorema de divergencia de Gauss para convertir una integral de superficie a una integral de volumen da
Para un volumen arbitrario el integrando se desvanece, y tenemos las ecuaciones de Cauchy de movimiento
Si un sistema está en equilibrio, el cambio en el momento con respecto al tiempo es igual a 0, ya que no hay aceleración.
o el uso de tensores,
Estas son las ecuaciones de equilibrio que se utilizan en mecánica de sólidos para la solución de problemas de elasticidad lineal. En la notación de ingeniería, las ecuaciones de equilibrio se expresan como
Conservación del momento lineal
La ley de conservación del momento lineal es una ley fundamental de la naturaleza, y se afirma que el momento total de un sistema cerrado de objetos (que no tiene interacciones con agentes externos) es constante. Una de las consecuencias de esto es que el centro de masa de cualquier sistema de objetos siempre seguirán con la misma velocidad a menos que actúe por una fuerza desde fuera del sistema.
La conservación del momento es una consecuencia matemática de la homogeneidad (turno simetría ) de espacio (posición en el espacio es la cantidad conjugado canónica a impulso). Por lo tanto, la conservación del momento se puede afirmar filosóficamente como "nada depende de la ubicación de por sí".
En un sistema aislado (uno donde las fuerzas externas están ausentes) la cantidad de movimiento total será constante: esto está implícito en Newton primera ley del movimiento. Tercera ley del movimiento de Newton, la ley de acciones recíprocas , que dicta que las fuerzas que actúan entre los sistemas son iguales en magnitud, pero de signo contrario, se debe a la conservación del momento.
Como la posición en el espacio es una cantidad vectorial, el impulso (siendo el conjugado canónica de posición) es una cantidad vectorial, así - tiene dirección. Por lo tanto, cuando se dispara un arma, el momento total final del sistema (la pistola y la bala) es el vector suma de los momentos de estos dos objetos. Suponiendo que la pistola y la bala había en reposo antes de disparar (lo que significa el impulso inicial del sistema era cero), el momento total final debe también igual a 0.
En un sistema aislado con sólo dos objetos, el cambio en el momento de un objeto debe ser igual y opuesta a la cambio en el momento del otro objeto. Matemáticamente,

Momentum tiene la característica especial de que, en un sistema cerrado, siempre se conserva, incluso en colisiones y separaciones causadas por las fuerzas explosivas. La energía cinética , por otro lado, no se conserva en las colisiones si son inelástica. Desde el momento se conserva que puede ser utilizado para calcular una velocidad desconocida después de una colisión o una separación si se conocen todas las otras masas y velocidades.
Un problema común en la física que requiere el uso de este hecho es la colisión de dos partículas. Desde impulso siempre se conserva, la suma de los momentos antes de la colisión debe ser igual a la suma de los momentos después del choque:
donde:
- u significa vector de velocidad antes del choque
- v significa vector de velocidad después de la colisión.
Por lo general, ya sea sólo conocemos las velocidades antes o después de una colisión y nos gustaría encontrar también fuera lo contrario. Correctamente la solución de este problema significa que usted tiene que saber lo que ocurrió tipo de colisión. Hay dos tipos básicos de colisiones, ambos de los cuales conservar el momento:
- Colisiones elásticas conservan la energía cinética, así como cantidad de movimiento total antes y después de la colisión.
- Colisiones inelásticas no conservan la energía cinética, pero el impulso total antes y después de la colisión se conserva.
Choques elásticos
Una colisión entre dos bolas de billar es un buen ejemplo de una colisión casi totalmente elástica. Además de impulso que se conserva cuando las dos bolas chocan, la suma de la energía cinética antes de una colisión debe ser igual a la suma de la energía cinética después de:
Puesto que el factor medio es común a todos los términos, puede ser sacado de inmediato.
Choque frontal (1 dimensional)
En el caso de dos objetos que chocan cabeza en encontramos que la velocidad final
que puede ser fácilmente reorganizado a
Caso especial: m 1 >> m 2
Consideremos ahora el caso cuando la masa de un cuerpo, por ejemplo 1 m, es mucho mayor que la de la otra, m 2 (m 1 m >> 2). En ese caso m 1 + m 2 es aproximadamente igual a 1 m y m 1 -m 2 es aproximadamente igual a 1 m.
Usando estas aproximaciones, la fórmula anterior para  se reduce a
se reduce a  . Su interpretación física es que en el caso de una colisión entre dos cuerpos, uno de los cuales es mucho más masivo que el otro, el cuerpo más ligero termina en movimiento en la dirección opuesta con el doble de la velocidad original del cuerpo más masivo.
. Su interpretación física es que en el caso de una colisión entre dos cuerpos, uno de los cuales es mucho más masivo que el otro, el cuerpo más ligero termina en movimiento en la dirección opuesta con el doble de la velocidad original del cuerpo más masivo.
Caso especial: m 1 = m 2
Otro caso especial es cuando la colisión es entre dos cuerpos de igual masa.
Diga m1 cuerpo que se mueve a una velocidad v 1 huelgas cuerpo m 2 que está en reposo (v 2). Poner este caso en la ecuación derivada arriba veremos que después de la colisión, el cuerpo que se movía (m 1) comenzará a moverse con velocidad v 2 y la masa m 2 empezará a moverse con velocidad v 1. Así que habrá un intercambio de velocidades.
Supongamos ahora que una de las masas, digamos m 2, estaba en reposo. En ese caso, después de la colisión el cuerpo en movimiento, m 1, vendrá a descansar y el cuerpo que estaba en reposo, m 2, empezará a moverse con la velocidad que M 1 tenían antes de la colisión.
Tenga en cuenta que todas estas observaciones son para una colisión elástica.
Este fenómeno se demuestra por Cuna de Newton, uno de los ejemplos más conocidos de la conservación del momento, un ejemplo de la vida real de este caso especial.
Colisiones multidimensionales
En el caso de objetos que chocan en más de una dimensión, como en las colisiones oblicuas, la velocidad se resuelve en componentes ortogonales con un componente perpendicular al plano de la colisión y el otro componente o componentes en el plano de colisión. Las componentes de la velocidad en el plano de colisión se mantienen sin cambios, mientras que la velocidad perpendicular al plano de colisión se calcula de la misma manera que el caso unidimensional.
Por ejemplo, en una colisión de dos dimensiones, los impulsos se puede descomponer en componentes x e y. Podemos entonces calcular cada componente por separado, y combinarlos para producir un resultado vector. La magnitud de este vector es el impulso final del sistema aislado.
Vea el página colisión elástica para más detalles. 
Colisiones inelásticas
Un ejemplo común de una colisión perfectamente inelástica es cuando dos bolas de nieve chocan y luego se pegan entre sí después. Esta ecuación describe la conservación del momento:
Se puede demostrar que una colisión perfectamente inelástica es uno en el que la cantidad máxima de energía cinética se convierte en otras formas. Por ejemplo, si ambos objetos se pegan entre sí después de la colisión y se mueven con una velocidad común final, uno puede siempre encontrar un marco de referencia en el que los objetos son llevados a descansar por la colisión y 100% de la energía cinética se convierte. Esto es cierto incluso en el caso relativista y utilizados en aceleradores de partículas para convertir eficientemente la energía cinética en las nuevas formas de masa-energía (es decir, para crear partículas masivas).
En caso de colisión inelástica, hay un parámetro adjunto llamado coeficiente de restitución (denotado por pequeñas 'e' o 'c' en muchos libros de texto). Se define como la relación de la velocidad relativa de separación a la velocidad relativa de enfoque. Se trata de una relación de por lo tanto es una cantidad adimensional.
Cuando tenemos una colisión elástica el valor de e (= coeficiente de restitución) es 1, es decir, la velocidad relativa de enfoque es la misma que la velocidad relativa de la separación de los cuerpos que chocan. En una colisión elástica se conserva la energía cinética del sistema.
Cuando una colisión no es elástica (e <1) se trata de una colisión inelástica. En caso de una colisión perfectamente inelástica la velocidad relativa de la separación del centro de masas de los cuerpos que chocan es 0. Por lo tanto después de la colisión de los cuerpos trabados entre sí después de la colisión. En caso de una colisión inelástica la pérdida de energía cinética es máxima como se indicó anteriormente.
En todo tipo de colisión si ninguna fuerza externa actúa sobre el sistema de cuerpos que chocan, el impulso siempre llegan conservado.
Explosiones
Una explosión se produce cuando un objeto se divide en dos o más fragmentos debido a una liberación de energía. Tenga en cuenta que la energía cinética en un sistema de explosión no se conserva, ya que implica la transformación de energía. (es decir, cambios de energía cinética en calor y energía del sonido)
http://www.glenbrook.k12.il.us/gbssci/phys/Class/momentum/u4l2e.html
En la demostración de cañón explosión, cantidad de movimiento total del sistema se conserva. El sistema consta de dos objetos - un cañón y una pelota de tenis. Antes de la explosión, el momento total del sistema es cero, ya que el cañón y la pelota de tenis situado en el interior de ella son tanto en reposo. Después de la explosión, el momento total del sistema todavía debe ser cero. Si la bola adquiere 50 unidades de impulso hacia adelante, entonces el cañón adquiere 50 unidades de atrás impulso. La suma vectorial de los momentos individuales de los dos objetos es 0. impulso total del sistema se conserva.
Vea el página colisión inelástica para más detalles.
Definiciones modernas de impulso
Momentum en mecánica relativista
En mecánica relativista, con el fin de ser conservado, el impulso debe ser definida como:
donde
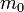 es el masa invariante del objeto en movimiento,
es el masa invariante del objeto en movimiento,  es el Factor de Lorentz
es el Factor de Lorentz  es la velocidad relativa entre un objeto y un observador
es la velocidad relativa entre un objeto y un observador  es la velocidad de la luz .
es la velocidad de la luz .
Momento relativista también se puede escribir como la masa por invariantes del objeto de velocidad adecuada, definida como la tasa de cambio de la posición del objeto en el marco de observador con respecto al tiempo transcurrido en los relojes de objeto (es decir, objeto el momento adecuado). Momento relativista se convierte en el impulso de Newton:  a baja velocidad
a baja velocidad  .
.
Relativista cuatro impulso como propone Albert Einstein surge de la invariancia de cuatro-vectores con la traducción de Lorentz. El de cuatro impulso se define como:
donde
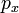 es el
es el  componente del momento relativista,
componente del momento relativista,  es la energía total del sistema:
es la energía total del sistema: 
La "longitud" del vector es la masa por la velocidad de la luz, que es invariable en todos los marcos de referencia:
Momentum de objetos sin masa
Objetos sin una masa en reposo, como los fotones , también llevan el impulso. La fórmula es:
donde
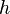 es La constante de Planck,
es La constante de Planck,  es el longitud de onda del fotón,
es el longitud de onda del fotón,  es la energía del fotón transporta y
es la energía del fotón transporta y  es la velocidad de la luz .
es la velocidad de la luz .
Generalización de impulso
Momentum es el Noether cargo de la invariancia traslacional. Como tal, incluso campos, así como otras cosas pueden tener impulso, no sólo partículas. Sin embargo, en espacio-tiempo curvo que no es asintóticamente Minkowski, el impulso no se define en absoluto.
Momentum en la mecánica cuántica
En la mecánica cuántica , el impulso se define como una operador en el función de onda. La Heisenberg principio de incertidumbre define los límites de la precisión con el impulso y la posición de un sistema único observable pueden ser conocidos a la vez. En la mecánica cuántica, la posición y el momento son variables conjugadas.
Para una sola partícula sin carga eléctrica y no giro, el operador impulso se puede escribir en la base posición como
donde:
 es el operador gradiente;
es el operador gradiente;  es el constante reducida de Planck;
es el constante reducida de Planck;  es la unidad imaginaria .
es la unidad imaginaria .
Esta es una forma comúnmente encontrado del operador de momento, aunque no el más general.
Momentum en electromagnetismo
Los campos eléctricos y magnéticos poseen impulso, independientemente de si son estáticas o que cambian en el tiempo. Es una gran sorpresa para estudiantes de primer año que se introducen en el bien conocido hecho de que la presión  de un campo electrostático (magnetostática) en una esfera de metal, la capacidad cilíndrica o bar ferromagnético:
de un campo electrostático (magnetostática) en una esfera de metal, la capacidad cilíndrica o bar ferromagnético:
donde  ,
, 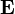 ,
,  , Son la densidad de energía electromagnética, campos eléctricos y magnéticos, respectivamente. La presión electromagnética
, Son la densidad de energía electromagnética, campos eléctricos y magnéticos, respectivamente. La presión electromagnética  puede ser suficientemente alta para explotar la capacidad. Así, los campos eléctricos y magnéticos no llevan impulso.
puede ser suficientemente alta para explotar la capacidad. Así, los campos eléctricos y magnéticos no llevan impulso.
Luz (visible, UV, radio) es una onda electromagnética y también tiene impulso. A pesar de que los fotones (el aspecto corpuscular de la luz) no tienen masa, todavía llevar impulso. Esto conduce a aplicaciones tales como la vela solar.
Momentum se conserva en un sistema electrodinámico (puede cambiar de un impulso en los campos para el impulso mecánico de las piezas en movimiento). El tratamiento de la dinámica de un campo generalmente se logra teniendo en cuenta el llamado tensor de energía-impulso y el cambio en el tiempo de la Vector de Poynting integra sobre un poco de volumen. Este es un campo tensor que tiene componentes relacionados con la densidad de energía y la densidad de momento.
El impulso canónica definición correspondiente al operador del momento de la mecánica cuántica cuando interactúa con el campo electromagnético es, utilizando el principio del mínimo de acoplamiento:
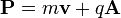 ,
,
en lugar de la habitual
 ,
,
donde:
 es el vector potencial electromagnético
es el vector potencial electromagnético  masa invariante de la partícula cargada
masa invariante de la partícula cargada 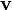 su velocidad
su velocidad  su carga.
su carga.





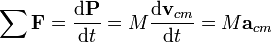


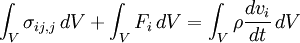


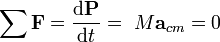

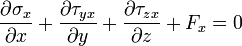
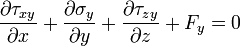

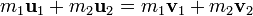
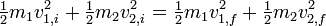

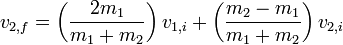


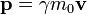

 . Tenga en cuenta que en la notación utilizada por el creador del diagrama, la masa invariante
. Tenga en cuenta que en la notación utilizada por el creador del diagrama, la masa invariante  está indexada por un cero,
está indexada por un cero, 
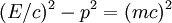
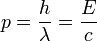
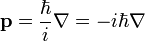
![P_ {static} = {W} = [{\ epsilon_0 \ epsilon} {\ frac {{\ mathbf E} ^ 2} {{2}}} + {\ frac {1} {{\ mu_0 \ mu}}} {\ frac {{\ mathbf B} ^ 2} {{2}}}],](../../images/160/16078.png)
