Fotón
Antecedentes de las escuelas de Wikipedia
Este contenido de Wikipedia ha sido seleccionada por SOS para su utilización en las escuelas de todo el mundo. Madres SOS cada aspecto después de un una familia de niños apadrinados .
 Fotones emitidos en una haz coherente de un láser | |
| Composición | Partícula elemental |
|---|---|
| Estadística | Bosonic |
| Interacciones | Electromagnético |
| Símbolo | γ, h ν, o ħ ω |
| Teorizado | Albert Einstein |
| Masa | 0 <1 × 10 -18 eV / c 2 |
| Vida media | Estable |
| Carga eléctrica | 0 <1 × 10 -35 e |
| Vuelta | 1 |
| Paridad | -1 |
| Paridad C | -1 |
| Condensado | I ( J P C) = 0,1 (1 -) |
Un fotón es una partícula elemental, el cuántica de la luz y todas las otras formas de radiación electromagnética , y la forzar portador para la fuerza electromagnética , incluso cuando estática a través de fotones virtuales. Los efectos de esta fuerza son fácilmente observable tanto en el microscópica y nivel macroscópico, porque el fotón no tiene masa en reposo; esto permite interacciones a largas distancias. Al igual que todas las partículas elementales, los fotones son actualmente explican mejor por la mecánica cuántica y de exposiciones la dualidad onda-partícula, las propiedades que exhiben tanto de olas y partículas. Por ejemplo, un único fotón puede ser refractada por una lente o exhibición onda interferencia con sí mismo, sino que también actúan como una partícula que da un resultado definitivo cuando su posición se mide.
El concepto moderno de fotón fue desarrollado gradualmente por Albert Einstein para explicar las observaciones experimentales que no encajaban en el clásico modelo de onda de la luz. En particular, el modelo de fotones representó la dependencia de la frecuencia de la energía de la luz, y explica la capacidad de la materia y la radiación para estar en equilibrio térmico. También representó observaciones anómalas, incluyendo las propiedades de la radiación del cuerpo negro, que otros físicos, sobre todo Max Planck , había tratado de explicar el uso de modelos semiclásicos, en el que la luz todavía es descrito por las ecuaciones de Maxwell , pero los objetos materiales que emiten y absorben la luz, hacerlo en cantidades de energía que se cuantifican (es decir, cambiar la energía sólo por ciertas cantidades discretas particulares y no se puede cambiar la energía de cualquier manera arbitraria). Aunque estos modelos semiclásicos contribuyeron al desarrollo de la mecánica cuántica, muchos otros experimentos a partir de Compton dispersión de fotones individuales por electrones, observadas por primera vez en 1923, validó la hipótesis de Einstein de que la luz misma es cuantizada. En 1926 el químico Gilbert N. Lewis acuñó el nombre de fotones de estas partículas, y después de 1927, cuando Arthur H. Compton ganó el Premio Nobel por sus estudios de dispersión, la mayoría de los científicos aceptan la validez que cuantos de luz tiene una existencia independiente, y fue aceptado Lewis fotón plazo para cuantos de luz.
En el Modelo Estándar de la física de partículas , los fotones son descritos como una consecuencia necesaria de las leyes físicas que tienen una cierta simetría en cada punto espacio tiempo. Las propiedades intrínsecas de los fotones, tales como carga , masa y giro, están determinadas por las propiedades de este medir la simetría. El concepto de fotón ha llevado a avances trascendentales en la física experimental y teórica, como láseres , La condensación de Bose-Einstein, la teoría cuántica de campos , y la interpretación probabilística de la mecánica cuántica. Se ha aplicado a fotoquímica, de alta resolución de la microscopía, y mediciones de distancias moleculares. Recientemente, los fotones han sido estudiados como elementos de las computadoras cuánticas y para aplicaciones sofisticadas comunicación óptico tal como criptografía cuántica.
Nomenclatura
| El modelo estándar de la física de partículas |
|---|
 Gran Colisionador de Hadrones del túnel CERN |
Fondo La física de partículas Modelo Estándar Teoría cuántica de campos Teoría Gauge Ruptura espontánea de simetría Mecanismo de Higgs |
Constituyentes Modelo electrodébil Cromodinámica cuántica Matriz CKM |
Limitaciones Problema CP fuerte Problema Jerarquía Las oscilaciones de neutrinos Ver también: Física más allá del Modelo Estándar |
Los científicos Rutherford · Thomson · Chadwick · Bose · Sudarshan · Koshiba · Davis, Jr. · Anderson · Fermi · Dirac · Feynman · Rubbia · Gell-Mann · Kendall · Taylor · Friedman · Powell · PW Anderson · Glashow · Meer · Cowan · Nambu · Chamberlain · Cabibbo · Schwartz · Perl · Majorana · Weinberg · Lee · Sala · Salam · Kobayashi · Maskawa · Yang · Yukawa · 'T Hooft · Veltman · · Bruto Politzer · Wilczek · Cronin · Fitch · Vleck · Higgs · Englert · Brout · Hagen · Guralnik · Kibble · Ting · Richter |
En 1900, Max Planck estaba trabajando en la radiación del cuerpo negro y sugirió que la energía de las ondas electromagnéticas sólo podría ser liberado en "paquetes" de energía. En su artículo de 1901 en Annalen der Physik llamó a estos paquetes de "elementos de energía". La palabra quanta (singular cuántica) se utilizó incluso antes de 1900 en el sentido de partículas o cantidades de diferentes cantidades , incluyendo la electricidad . Más tarde, en 1905 Albert Einstein fue más allá al sugerir que las ondas electromagnéticas sólo podían existir en estos discretos paquetes de onda. Llamó a un tal ola -packet los cuántica luz (alemán: das Lichtquant). El nombre deriva del fotón palabra griega para la luz, φῶς (Phos transliterados), y fue acuñado en 1926 por el químico físico Gilbert Lewis, quien publicó una teoría especulativa en la que los fotones eran "increable e indestructible". Aunque la teoría de Lewis nunca fue aceptada ya que se contradice con muchos experimentos, su nuevo nombre, fotones, fue adoptado inmediatamente por la mayoría de los físicos. Isaac Asimov créditos Arthur Compton con la definición de cuantos de energía en forma de fotones en 1923.
En física, un fotón es denotado generalmente por el símbolo γ (la letra griega gamma). Este símbolo para el fotón deriva probablemente de rayos gamma, que fueron descubiertas en 1900 por Paul Villard, nombrado por Ernest Rutherford en 1903, y demostró ser una forma de radiación electromagnética en 1914 por Rutherford y Eduardo Andrade. En la química y ingeniería óptica, los fotones son usualmente simbolizados por hv, la energía de un fotón, donde h es Constante y la de Planck letra griega ν ( nu) es el fotón de frecuencia. Mucho menos común, el fotón puede ser simbolizado por hf, donde su frecuencia es denotada por f.
Propiedades físicas
El fotón es sin masa, no tiene carga eléctrica , y es estable. Un fotón tiene dos posibles estados de polarización y es descrito por exactamente tres parámetros continuos: los componentes de su vector de onda, que determinan su longitud de onda λ y su dirección de propagación. El fotón es la bosón de norma para el electromagnetismo , y por lo tanto todos los demás números cuánticos de los fotones (como número de leptones, número de bariones, y números cuánticos sabor) son cero.
Los fotones son emitidos en muchos procesos naturales. Por ejemplo, cuando una carga se aceleró emite radiación sincrotrón. Durante un molecular , atómica o nuclear transición a una menor nivel de energía, los fotones de varias energía se emite, desde luz infrarroja para rayos gamma. Un fotón también puede ser emitido cuando una partícula y su correspondiente antipartícula son aniquilado (por ejemplo, aniquilación electrón-positrón).
En el espacio vacío, el fotón se mueve en c (la velocidad de la luz ) y su energía y el impulso están relacionados por E = pc, donde p es el magnitud del momento vector p. Esto se deriva de la siguiente relación relativista, con m = 0:
La energía y el impulso de un fotón dependen sólo de su frecuencia (ν) o inversamente, su longitud de onda (λ):
donde k es el vector de onda (donde el número de onda k = | k | = 2π / λ), ω = 2π ν es la frecuencia angular, y H = h / 2π es la constante reducida de Planck.
Puesto que P puntos en la dirección de propagación del fotón, la magnitud del momento es
El fotón también lleva momento angular de espín que no depende de su frecuencia. La magnitud de su giro es 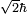 y el componente mide a lo largo de su dirección de movimiento, su helicidad, debe ser ± h. Estos dos helicidades posibles, llamados diestro y zurdo, corresponden a los dos posibles estados de polarización circulares del fotón.
y el componente mide a lo largo de su dirección de movimiento, su helicidad, debe ser ± h. Estos dos helicidades posibles, llamados diestro y zurdo, corresponden a los dos posibles estados de polarización circulares del fotón.
Para ilustrar la importancia de estas fórmulas, la aniquilación de una partícula con su antipartícula en el espacio libre debe dar lugar a la creación de al menos dos fotones por la siguiente razón. En el centro de masa marco, las antipartículas que colisionan no tienen ningún momento neto, mientras que un solo fotón siempre tiene un momento (ya que está determinado, como hemos visto, sólo por la frecuencia o longitud de onda del fotón-que no puede ser cero). Por lo tanto, la conservación del momento (o equivalentemente, invariancia traslacional) requiere que se crean al menos dos fotones, con progresión neta cero. (Sin embargo, es posible si el sistema interactúa con otra partícula o campo para la aniquilación para producir un fotón, como cuando un positrón aniquila con un electrón atómico unido, es posible para un solo fotón para ser emitida, como los saltos de campo de Coulomb nucleares simetría traslacional.) La energía de los dos fotones, o, de manera equivalente, su frecuencia, puede determinarse a partir conservación de cuatro impulso. Visto de otra manera, el fotón puede considerarse como su propia antipartícula. El proceso inverso, la producción de pares, es el mecanismo dominante por el cual los fotones de alta energía, como rayos gamma pierden energía mientras pasa a través de materia. Ese proceso es el inverso de la "aniquilación de un fotón" permitido en el campo eléctrico de un núcleo atómico.
Las fórmulas clásicas para la energía y el impulso de la radiación electromagnética pueden ser re-expresados en términos de eventos de fotones. Por ejemplo, el la presión de la radiación electromagnética sobre un objeto deriva de la transferencia de momento de fotones por unidad de tiempo y unidad de área a ese objeto, ya que la presión es la fuerza por unidad de área y la fuerza es el cambio en el impulso por unidad de tiempo.
Comprobaciones experimentales sobre la masa del fotón
El fotón se entiende actualmente que ser estrictamente sin masa, pero esto es una cuestión experimental. Si el fotón no es una partícula sin masa estrictamente, no se movería a la velocidad exacta de la luz en el vacío, c. Su velocidad sería inferior y dependerá de su frecuencia. Relatividad no se vería afectada por esta; la velocidad de llamada de la luz, c, entonces no puede ser la velocidad real a la que la luz se mueve, sino una constante de la naturaleza que es la velocidad máxima que cualquier objeto puede alcanzar teóricamente en el espacio-tiempo. Por lo tanto, todavía sería la velocidad de las ondas del espacio-tiempo ( ondas gravitacionales y gravitones), pero no sería la velocidad de fotones.
Un fotón masiva tendría otros efectos también. ley de Coulomb sería modificado y el campo electromagnético tendría un grado extra de libertad física. Estos efectos producen sondas experimentales más sensibles de la masa del fotón que la dependencia de la frecuencia de la velocidad de la luz. Si la ley de Coulomb no es exactamente válida, a continuación, que causaría la presencia de un campo eléctrico dentro de un conductor hueco cuando se somete a un campo eléctrico externo. Esto por lo tanto uno permite probar la ley de Coulomb de muy alta precisión. Un resultado nulo de tal experimento ha establecido un límite de 10 m ≲ -14 eV / c2.
Límites superiores Sharper se han obtenido en los experimentos diseñados para detectar los efectos causados por el galáctico potencial vector. Aunque el potencial galáctico vector es muy grande ya que el galáctico existe campo magnético sobre escalas de longitud muy largas, sólo el campo magnético es observable si el fotón es sin masa. En el caso de un fotón masiva, el término masa  afectaría el plasma galáctico. El hecho de que no se observan tales efectos implica un límite superior en la masa del fotón de m <3 × 10 -27 eV / c2. El potencial galáctico vector también se puede probar directamente midiendo el par ejercido sobre un anillo magnetizado. Tales métodos se utilizaron para obtener el límite superior más nítida de 10 -18 eV / c 2 (el equivalente a 1,07 × 10 -27 unidades de masa atómica) propuesta por el Particle Data Group.
afectaría el plasma galáctico. El hecho de que no se observan tales efectos implica un límite superior en la masa del fotón de m <3 × 10 -27 eV / c2. El potencial galáctico vector también se puede probar directamente midiendo el par ejercido sobre un anillo magnetizado. Tales métodos se utilizaron para obtener el límite superior más nítida de 10 -18 eV / c 2 (el equivalente a 1,07 × 10 -27 unidades de masa atómica) propuesta por el Particle Data Group.
Estos límites afilados de la no observación de los efectos causados por el potencial vector galáctico han demostrado ser dependiente del modelo. Si se genera la masa del fotón a través de la Mecanismo de Higgs, entonces el límite superior de m ≲10 -14 eV / c 2 de la prueba de la ley de Coulomb es válida.
Los fotones dentro de los superconductores hacen desarrollar un distinto de cero masa efectiva resto; Como resultado, las fuerzas electromagnéticas se convierten en superconductores de corto alcance en el interior.
Desarrollo histórico

En la mayoría de las teorías hasta el siglo XVIII, la luz era representado como siendo compuesto de partículas. Desde modelos de partículas no pueden explicar fácilmente el refracción, la difracción y birrefringencia de la luz, las teorías de onda de la luz fueron propuestas por René Descartes (1637), Robert Hooke (1665), y Christian Huygens (1678); Sin embargo, los modelos de partículas permanecieron dominante, principalmente debido a la influencia de Isaac Newton . A principios del siglo XIX, Thomas Young y Agosto Fresnel demostró claramente la interferencia y la difracción de la luz y por 1.850 modelos de olas eran generalmente aceptadas. En 1865, James Clerk Maxwell 's predicción que la luz era una onda electromagnética, lo cual fue confirmado experimentalmente en 1888 por Detección de Heinrich Hertz de las ondas de radio me parecieron ser el golpe final a los modelos de partículas de luz.

La Teoría ondulatoria de Maxwell, sin embargo, no tener en cuenta todas las propiedades de la luz. La teoría de Maxwell predice que la energía de una onda de luz depende sólo de su intensidad, no en su frecuencia; Sin embargo, varios tipos independientes de experimentos muestran que la energía impartida por la luz a los átomos depende sólo de la frecuencia de la luz, no de su intensidad. Por ejemplo, algunas reacciones químicas son provocados sólo por la luz de frecuencia superior a un cierto umbral; luz de frecuencia más baja que el umbral, no importa qué tan intenso, no iniciar la reacción. Del mismo modo, los electrones pueden ser expulsados de una placa de metal por el resplandor de la luz de frecuencia suficientemente alta en ella (la efecto fotoeléctrico); la energía del electrón expulsado se relaciona únicamente con la frecuencia de la luz, no a su intensidad.
Al mismo tiempo, las investigaciones de radiación de cuerpo negro llevó a cabo durante cuatro décadas (1860-1900) por varios investigadores culminó con Max Planck 's hipótesis de que la energía de cualquier sistema que absorbe o emite radiación electromagnética de frecuencia ν es un múltiplo entero de un cuanto de energía E = hv. Como se muestra por Albert Einstein , alguna forma de cuantización de la energía se debe asumir para tener en cuenta el equilibrio térmico observado entre la materia y la radiación electromagnética ; para esta explicación de la efecto fotoeléctrico, Einstein recibió el 1921 Premio Nobel de Física.
Desde la teoría de Maxwell de la luz permite que todos los posibles energías de radiación electromagnética, la mayoría de los físicos supone inicialmente que la cuantización de la energía como resultado de alguna restricción desconocida en la materia que absorbe o emite la radiación. En 1905, Einstein fue el primero en proponer que cuantización de la energía era una propiedad de la propia radiación electromagnética. Aunque aceptó la validez de la teoría de Maxwell, Einstein señaló que muchos experimentos anómalas podrían explicarse si la energía de una onda de luz de Maxwell fueron localizados en puntos como quanta que se mueven independientemente uno de otro, incluso si la propia onda se extiende continuamente a lo largo espacio. En 1909 y 1916, Einstein demostró que, si La ley de Planck de la radiación del cuerpo negro es aceptada, los cuantos de energía también debe llevar el impulso p = h / λ, haciéndolos de pleno derecho partículas. Este momento del fotón se observó experimentalmente por Arthur Compton, por la que recibió el Premio Nobel en 1927. La pregunta fundamental era entonces: cómo unificar la teoría ondulatoria de la luz de Maxwell con su naturaleza corpuscular observada experimentalmente? La respuesta a esta pregunta ocupaba Albert Einstein para el resto de su vida, y se resolvió en electrodinámica cuántica y su sucesor, el modelo estándar (ver Segunda cuantización y El fotón como un bosón de calibre , más adelante).
Las primeras objeciones

1905 las predicciones de Einstein fueron verificadas experimentalmente de varias maneras en las dos primeras décadas del siglo 20, como se relata en Conferencia Nobel de Robert Millikan. Sin embargo, antes El experimento de Compton mostrando que los fotones llevaron impulso proporcional a su número de onda (o frecuencia) (1922), la mayoría de los físicos eran reacios a creer que la radiación electromagnética en sí podría ser de partículas. (Véase, por ejemplo, las conferencias Nobel de Wien, Planck y Millikan.). En su lugar, existía la creencia generalizada de que la cuantización de la energía se debió a alguna restricción desconocida sobre la materia que absorbe o emite radiación. Las actitudes cambian con el tiempo. En parte, el cambio se puede remontar a experimentos como Dispersión de Compton, donde era mucho más difícil no atribuir cuantización a la luz en sí para explicar los resultados observados.
Incluso después de que el experimento de Compton, Niels Bohr , Hendrik Kramers y John Slater hizo un último intento de preservar el modelo electromagnético continuo de Maxwell campo de la luz, la denominada solución de Modelo BKS. Para dar cuenta de los datos entonces disponibles, dos hipótesis drásticas había que hacer:
- Energía y el momento se conservan sólo en la media en las interacciones entre la materia y la radiación, no en procesos elementales tales como absorción y emisión. Esto permite conciliar la energía discontinua cambiante del átomo (salto entre estados de energía) con la liberación continua de energía en radiación.
- La causalidad es abandonado. Por ejemplo, las emisiones espontáneas son meramente emisiones inducidas por un campo electromagnético "virtual".
Sin embargo, los experimentos de Compton refinados mostraron que la energía-momento se conserva extraordinariamente bien en procesos elementales; y también que el traqueteo del electrón y la generación de un nuevo fotón en Dispersión Compton obedecen a la causalidad dentro de 10 ps. En consecuencia, Bohr y sus compañeros de trabajo dieron su modelo "como un funeral honorable como sea posible". Sin embargo, los fracasos del modelo BKS inspiró Werner Heisenberg en su desarrollo de la mecánica matricial.
Unos físicos persistieron en el desarrollo de modelos semiclásicos en el que la radiación electromagnética no está cuantificado, pero la materia parece obedecer las leyes de la mecánica cuántica . Aunque la evidencia de los fotones de experimentos químicos y físicos fue abrumadora por la década de 1970, esta evidencia no puede ser considerada como absolutamente definitiva; ya que se basaba en la interacción de la luz con la materia, suficientemente complicada teoría de la materia podría, en principio cuenta de la evidencia. Sin embargo, todas las teorías semiclásicos fueron refutadas definitivamente en los años 1970 y 1980 por los experimentos de correlación de fotones. Por lo tanto, la hipótesis de Einstein de que la cuantificación es una propiedad de la luz misma se considera que se ha demostrado.
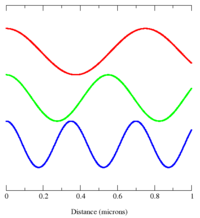
Principios dualidad onda-partícula y la incertidumbre
Los fotones, como todos los objetos cuánticos, presentan tanto propiedades ondulatorias y similares a las partículas. Su naturaleza dual onda-partícula puede ser difícil de visualizar. Fenómenos Las pantallas de fotones claramente ondulada como la difracción y la interferencia en la escala de longitud de su longitud de onda. Por ejemplo, un solo fotón que pasa a través de una de la doble rendija experimento tierras en la pantalla que muestra fenómenos de interferencia, pero sólo si hay una medida se hizo sobre la hendidura real que se ejecutan a través. Para tener en cuenta la interpretación partícula que fenómeno se llama distribución de probabilidad , pero se comporta de acuerdo con las ecuaciones de Maxwell . Sin embargo, los experimentos confirman que el fotón no es un corto pulso de radiación electromagnética; que no se propague a cabo cuando se propaga, ni dividir cuando encuentra un divisor de haz. Más bien, el fotón parece ser una punto de partícula similar ya que se absorbe o emite como un todo por arbitrariamente pequeños sistemas, sistemas mucho más pequeñas que su longitud de onda, tales como un núcleo atómico (≈10 -15 m de diámetro) o incluso el punto de como electrones . Sin embargo, el fotón no es una partícula puntual cuya trayectoria está conformada por el probabilísticamente campo electromagnético, como es concebido por Einstein y otros; esa hipótesis también fue refutada por los experimentos de correlación de fotones antes citadas. Según los conocimientos actuales, el propio campo electromagnético es producido por los fotones, lo que a su vez resultado de un local medir la simetría y las leyes de la teoría cuántica de campos (véase la Segunda cuantización y calibrador bosón secciones a continuación).

Un elemento clave de la mecánica cuántica es Heisenberg principio de incertidumbre, que prohíbe la medición simultánea de la posición y el momento de una partícula a lo largo de la misma dirección. Cabe destacar que el principio de incertidumbre, para partículas materiales cargadas requiere la cuantización de la luz en fotones, e incluso la dependencia de la frecuencia de la energía del fotón y el momento. Un elegante ilustración es de Heisenberg pensado experimento para localizar un electrón con un microscopio ideal. La posición del electrón se puede determinar dentro de la poder de resolución del microscopio, que está dada por una fórmula de clásicos ópticas
donde  es el ángulo de apertura del microscopio. Por lo tanto, la incertidumbre de la posición
es el ángulo de apertura del microscopio. Por lo tanto, la incertidumbre de la posición  se puede hacer arbitrariamente pequeño mediante la reducción de la longitud de onda λ. El impulso del electrón es incierto, ya que recibió una "patada"
se puede hacer arbitrariamente pequeño mediante la reducción de la longitud de onda λ. El impulso del electrón es incierto, ya que recibió una "patada"  de la dispersión de la luz de ella en el microscopio. Si la luz no se cuantifica en fotones, la incertidumbre
de la dispersión de la luz de ella en el microscopio. Si la luz no se cuantifica en fotones, la incertidumbre  podría hacerse arbitrariamente pequeña reducción de la intensidad de la luz. En ese caso, ya que la longitud de onda y la intensidad de la luz se pueden variar de forma independiente, se podría determinar simultáneamente la posición y el impulso para arbitrariamente alta precisión, la violación de la principio de incertidumbre. Por el contrario, la fórmula de Einstein para el impulso del fotón preserva el principio de incertidumbre; desde el fotón se dispersa en cualquier lugar dentro de la abertura, la incertidumbre de impulso transferido iguales
podría hacerse arbitrariamente pequeña reducción de la intensidad de la luz. En ese caso, ya que la longitud de onda y la intensidad de la luz se pueden variar de forma independiente, se podría determinar simultáneamente la posición y el impulso para arbitrariamente alta precisión, la violación de la principio de incertidumbre. Por el contrario, la fórmula de Einstein para el impulso del fotón preserva el principio de incertidumbre; desde el fotón se dispersa en cualquier lugar dentro de la abertura, la incertidumbre de impulso transferido iguales
dando el producto  , Que es el principio de incertidumbre de Heisenberg. Por lo tanto, el mundo entero está cuantificada; Tanto la materia y los campos deben obedecer un conjunto coherente de leyes cuánticas, si cualquiera de ellos es a cuantificar.
, Que es el principio de incertidumbre de Heisenberg. Por lo tanto, el mundo entero está cuantificada; Tanto la materia y los campos deben obedecer un conjunto coherente de leyes cuánticas, si cualquiera de ellos es a cuantificar.
El principio de incertidumbre análoga para los fotones prohíbe la medición simultánea de la serie  de fotones (ver Estado de Fock y la Segunda cuantización sección de abajo) en una onda electromagnética y la fase
de fotones (ver Estado de Fock y la Segunda cuantización sección de abajo) en una onda electromagnética y la fase  de esa ola
de esa ola
Ver estado coherente y exprimido estado coherente para más detalles.
Ambos fotones y partículas materiales como los electrones crean análoga patrones de interferencia cuando pasan a través de una experimento de la doble rendija. Para fotones, esto corresponde a la interferencia de una Onda de luz Maxwell mientras que, para las partículas materiales, esto corresponde a la interferencia de la Ecuación de onda de Schrödinger. Aunque esta similitud podría sugerir que las ecuaciones de Maxwell son simplemente la ecuación de Schrödinger para los fotones, la mayoría de los físicos no están de acuerdo. Por un lado, son matemáticamente diferentes; más obviamente, una ecuación de Schrödinger resuelve un complejo campo, mientras que cuatro ecuaciones de Maxwell para resolver verdaderos campos. Más en general, el concepto normal de un Schrödinger probabilidad función de onda no puede aplicarse a los fotones. Siendo sin masa, no pueden ser localizados sin ser destruido; técnicamente, los fotones no pueden tener una posición eigenstate  Y, por lo tanto, el principio de incertidumbre de Heisenberg normales
Y, por lo tanto, el principio de incertidumbre de Heisenberg normales  no pertenece a los fotones. Unas pocas funciones de onda de sustitución se han sugerido para el fotón, pero no han entrado en uso general. En cambio, los físicos aceptan generalmente el segundo cuantificado teoría de los fotones se describe a continuación, electrodinámica cuántica, en la que los fotones son excitaciones cuantizadas de modos electromagnéticos.
no pertenece a los fotones. Unas pocas funciones de onda de sustitución se han sugerido para el fotón, pero no han entrado en uso general. En cambio, los físicos aceptan generalmente el segundo cuantificado teoría de los fotones se describe a continuación, electrodinámica cuántica, en la que los fotones son excitaciones cuantizadas de modos electromagnéticos.
Modelo de Bose-Einstein de un gas de fotones
En 1924, Satyendra Nath Bose deriva La ley de Planck de la radiación del cuerpo negro sin utilizar ningún electromagnetismo, sino más bien una modificación de conteo de grano grueso espacio de fase. Einstein demostró que esta modificación es equivalente a suponer que los fotones son rigurosamente idénticos y que implicaba una "interacción no local misteriosa", ahora entendida como el requisito de una estado mecánico cuántico simétrica. Este trabajo llevó al concepto de estados coherentes y el desarrollo del láser. En los mismos documentos, Einstein amplió el formalismo de Bose a partículas materiales ( bosones) y predijo que iban a condensar en su estado más bajo cuántica a temperaturas suficientemente bajas; este Bose-Einstein fue observado experimentalmente en 1995. Más tarde fue utilizado por Lene Hau para frenar, y luego se detiene por completo, la luz en 1999 y 2001.
La visión moderna sobre este tema es que los fotones son, en virtud de su espín entero, bosones (a diferencia de fermiones de spin semi-entero). Por el spin-estadísticas teorema, todos los bosones obedecen a la estadística de Bose-Einstein (mientras que todos los fermiones obedecen Fermi-Dirac estadísticas).
Estimulado y emisión espontánea
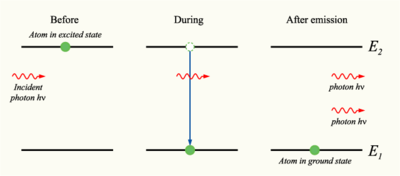
En 1916, Einstein demostró que la ley de radiación de Planck podría derivarse de un tratamiento semi-clásica, estadística de fotones y átomos, lo que implica una relación entre las tasas a las que los átomos emiten y absorben los fotones. La condición se deduce de la suposición de que la luz es emitida y absorbida por átomos de forma independiente, y que el equilibrio térmico se conserva por la interacción con los átomos. Considere una cavidad en equilibrio térmico y lleno de radiación electromagnética y los átomos que pueden emitir y absorber esa radiación. El equilibrio térmico requiere que la densidad de energía  de fotones con frecuencia
de fotones con frecuencia  (Que es proporcional a su densidad numérica) es, en promedio, constante en el tiempo; Por lo tanto, la velocidad a la que se emiten fotones de una frecuencia particular, debe ser igual a la tasa de absorción de las mismas.
(Que es proporcional a su densidad numérica) es, en promedio, constante en el tiempo; Por lo tanto, la velocidad a la que se emiten fotones de una frecuencia particular, debe ser igual a la tasa de absorción de las mismas.
Einstein comenzó postulando las relaciones de proporcionalidad simples para las diferentes velocidades de reacción implicadas. En su modelo, la tasa 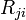 para un sistema para absorber un fotón de frecuencia
para un sistema para absorber un fotón de frecuencia  y la transición de una energía más baja
y la transición de una energía más baja  a una energía más alto
a una energía más alto  es proporcional al número
es proporcional al número  de átomos con energía
de átomos con energía  y para la densidad de energía
y para la densidad de energía  de fotones ambiente con esa frecuencia,
de fotones ambiente con esa frecuencia,
donde  es el tasa constante para la absorción. Para el proceso inverso, hay dos posibilidades: la emisión espontánea de un fotón, y un retorno al estado de baja energía que se inicia por la interacción con un fotón de paso. Siguiendo el enfoque de Einstein, la tasa correspondiente
es el tasa constante para la absorción. Para el proceso inverso, hay dos posibilidades: la emisión espontánea de un fotón, y un retorno al estado de baja energía que se inicia por la interacción con un fotón de paso. Siguiendo el enfoque de Einstein, la tasa correspondiente  para la emisión de fotones de frecuencia
para la emisión de fotones de frecuencia  y la transición de una energía superior
y la transición de una energía superior  a una energía más baja
a una energía más baja  es
es
donde 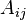 es la constante de velocidad para emitiendo un fotón de forma espontánea, y
es la constante de velocidad para emitiendo un fotón de forma espontánea, y  es la constante de velocidad para emitir en respuesta a los fotones ambiente ( inducido o emisión estimulada). En equilibrio termodinámico, el número de átomos en el estado i y el de los átomos en el estado j debe, en promedio, ser constante; Por lo tanto, las tasas
es la constante de velocidad para emitir en respuesta a los fotones ambiente ( inducido o emisión estimulada). En equilibrio termodinámico, el número de átomos en el estado i y el de los átomos en el estado j debe, en promedio, ser constante; Por lo tanto, las tasas 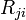 y
y  debe ser igual. También, por los argumentos análogos a la derivación de Estadísticas de Boltzmann, la relación de
debe ser igual. También, por los argumentos análogos a la derivación de Estadísticas de Boltzmann, la relación de  y
y  es
es 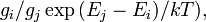 donde
donde  son los degeneración del estado i y el de j, respectivamente,
son los degeneración del estado i y el de j, respectivamente,  sus energías, k el Constante de Boltzmann y T del sistema temperatura . De esto, se deriva fácilmente que
sus energías, k el Constante de Boltzmann y T del sistema temperatura . De esto, se deriva fácilmente que  y
y
El A y B se conocen colectivamente como los coeficientes de Einstein.
Einstein no podía justificar plenamente sus ecuaciones de velocidad, pero afirmó que debería ser posible calcular los coeficientes 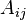 ,
,  y
y  una vez que los físicos habían obtenido "la mecánica y electrodinámica modificadas para adaptarse a la hipótesis cuántica". De hecho, en 1926, Paul Dirac derivó el
una vez que los físicos habían obtenido "la mecánica y electrodinámica modificadas para adaptarse a la hipótesis cuántica". De hecho, en 1926, Paul Dirac derivó el  constantes de velocidad en el uso de un enfoque semiclásico, y, en 1927, tuvieron éxito en la obtención de todas las constantes de velocidad de los primeros principios en el marco de la teoría cuántica. El trabajo de Dirac fue la fundación de la electrodinámica cuántica, es decir, la cuantificación del propio campo electromagnético. El enfoque de Dirac también se llama segunda cuantización o teoría cuántica de campos ; tratamientos mecánicos cuánticos anteriores sólo tratan partículas materiales como, no el campo electromagnético de la mecánica cuántica.
constantes de velocidad en el uso de un enfoque semiclásico, y, en 1927, tuvieron éxito en la obtención de todas las constantes de velocidad de los primeros principios en el marco de la teoría cuántica. El trabajo de Dirac fue la fundación de la electrodinámica cuántica, es decir, la cuantificación del propio campo electromagnético. El enfoque de Dirac también se llama segunda cuantización o teoría cuántica de campos ; tratamientos mecánicos cuánticos anteriores sólo tratan partículas materiales como, no el campo electromagnético de la mecánica cuántica.
Einstein estaba preocupado por el hecho de que su teoría parecía incompleta, ya que no determinó la dirección de un fotón emitido espontáneamente. Una naturaleza probabilística de movimiento de partículas de luz se consideró por primera vez por Newton en su tratamiento de birrefringencia y, más generalmente, de la separación de haces de luz en las interfaces en un haz transmitido y un haz reflejado. Newton planteó la hipótesis de que las variables ocultas en la partícula de luz determinan cuál es el camino que seguiría. Del mismo modo, Einstein esperaba una teoría más completa que dejar nada al azar, a partir de su separación de la mecánica cuántica. Irónicamente, Max Born, interpretación probabilística de la función de onda se inspiró en la obra posterior de Einstein en busca de una teoría más completa.
Segunda cuantización
En 1910, Peter Debye deriva La ley de Planck de la radiación del cuerpo negro a partir de una suposición relativamente simple. Él correctamente descompone el campo electromagnético en una cavidad en su Modos de Fourier, y se supone que la energía en cualquier modo era un múltiplo entero de  , Donde
, Donde  es la frecuencia del modo electromagnético. La ley de Planck de la radiación del cuerpo negro sigue inmediatamente como una suma geométrica. Sin embargo, el enfoque de Debye no dio la fórmula correcta para las fluctuaciones de la energía de la radiación del cuerpo negro, que fueron derivados por Einstein en 1909.
es la frecuencia del modo electromagnético. La ley de Planck de la radiación del cuerpo negro sigue inmediatamente como una suma geométrica. Sin embargo, el enfoque de Debye no dio la fórmula correcta para las fluctuaciones de la energía de la radiación del cuerpo negro, que fueron derivados por Einstein en 1909.
En 1925, Nacido, Heisenberg y Jordan reinterpretado el concepto de Debye en una forma clave. Como se muestra clásica, la Modos de Fourier de la campo electromagnético de un conjunto completo de ondas electromagnéticas planas indexados por su vector de onda k y la polarización del estado son equivalentes a un conjunto de desacoplado osciladores armónicos simples. Cuántica tratada mecánicamente, los niveles de energía de tales osciladores son conocidos por ser  , Donde
, Donde  es la frecuencia del oscilador. El nuevo paso clave fue identificar un modo electromagnético con energía
es la frecuencia del oscilador. El nuevo paso clave fue identificar un modo electromagnético con energía  como un estado con
como un estado con  fotones, cada uno de energía
fotones, cada uno de energía  . Este enfoque da la fórmula fluctuación de energía correcta.
. Este enfoque da la fórmula fluctuación de energía correcta.

Dirac llevó un paso más allá. Se trató la interacción entre una carga y un campo electromagnético como una pequeña perturbación que induce transiciones en los estados de fotones, cambiando el número de fotones en los modos, mientras que la conservación de energía y el momento en general. Dirac pudo derivar de Einstein 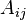 y
y  coeficientes de los primeros principios, y mostraron que las estadísticas de Bose-Einstein de fotones es una consecuencia natural de la cuantización del campo electromagnético correctamente (el razonamiento de Bose fue en la dirección opuesta, sino que deriva La ley de Planck de la radiación del cuerpo negro asumiendo estadísticas B-E). En el tiempo de Dirac, todavía no se sabía que todos los bosones, incluidos los fotones, deben obedecer la estadística de Bose-Einstein.
coeficientes de los primeros principios, y mostraron que las estadísticas de Bose-Einstein de fotones es una consecuencia natural de la cuantización del campo electromagnético correctamente (el razonamiento de Bose fue en la dirección opuesta, sino que deriva La ley de Planck de la radiación del cuerpo negro asumiendo estadísticas B-E). En el tiempo de Dirac, todavía no se sabía que todos los bosones, incluidos los fotones, deben obedecer la estadística de Bose-Einstein.
De segundo orden de Dirac teoría de la perturbación puede implicar fotones virtuales, estados intermedios transitorios del campo electromagnético; los estáticas eléctricas y magnéticas interacciones están mediadas por tales fotones virtuales. En tales teorías cuánticas de campos , la amplitud de probabilidad de eventos observables se calcula sumando sobre todos los posibles pasos intermedios, incluso los que son no físico; por lo tanto, los fotones virtuales no están obligados a satisfacer  , y pueden tener extras estados de polarización; dependiendo del calibre usado, los fotones virtuales pueden tener tres o cuatro estados de polarización, en vez de los dos estados de fotones reales. Aunque estos fotones virtuales transitorios nunca pueden ser observados, contribuyen apreciablemente a las probabilidades de eventos observables. De hecho, como de segundo orden y los cálculos de perturbación de orden superior pueden dar aparentemente infinitas contribuciones a la suma. Tales resultados no físicos se corrigen para el uso de la técnica de la renormalización . Otras partículas virtuales pueden contribuir a la suma así; por ejemplo, dos fotones pueden interactuar indirectamente a través virtual de electrones - positrón pares. De hecho, como la dispersión de fotones-fotón, así como la dispersión de electrones-fotón, está destinado a ser uno de los modos de operación de la acelerador de partículas previsto, el Colisionador Lineal Internacional.
, y pueden tener extras estados de polarización; dependiendo del calibre usado, los fotones virtuales pueden tener tres o cuatro estados de polarización, en vez de los dos estados de fotones reales. Aunque estos fotones virtuales transitorios nunca pueden ser observados, contribuyen apreciablemente a las probabilidades de eventos observables. De hecho, como de segundo orden y los cálculos de perturbación de orden superior pueden dar aparentemente infinitas contribuciones a la suma. Tales resultados no físicos se corrigen para el uso de la técnica de la renormalización . Otras partículas virtuales pueden contribuir a la suma así; por ejemplo, dos fotones pueden interactuar indirectamente a través virtual de electrones - positrón pares. De hecho, como la dispersión de fotones-fotón, así como la dispersión de electrones-fotón, está destinado a ser uno de los modos de operación de la acelerador de partículas previsto, el Colisionador Lineal Internacional.
En la notación de la física moderna, elestado cuántico del campo electromagnético se escribe como unestado de Fock, unproducto tensorial de los estados para cada modo electromagnético
donde  representa el estado en el que
representa el estado en el que los fotones están en el modo
los fotones están en el modo .En esta notación, la creación de un nuevo fotón en modo
.En esta notación, la creación de un nuevo fotón en modo (por ejemplo, emitida por una transición atómica) se escribe como
(por ejemplo, emitida por una transición atómica) se escribe como .Esta notación simplemente expresa el concepto de Born, Heisenberg y Jordan se ha descrito anteriormente, y no añade ningún física.
.Esta notación simplemente expresa el concepto de Born, Heisenberg y Jordan se ha descrito anteriormente, y no añade ningún física.
Las propiedades hadrónicas del fotón
Las mediciones de la interacción entre fotones energéticos y hadrones muestran que la interacción es mucho más intensa de lo esperado por la interacción de los fotones con meramente carga eléctrica de la hadrones. Además, la interacción de los fotones energéticos con protones es similar a la interacción de los fotones con neutrones a pesar del hecho de que las estructuras de carga eléctrica de los protones y los neutrones son sustancialmente diferentes.
Una teoría llamada Vector Meson Dominación (VMD) se desarrolló para explicar este efecto. Según VMD, el fotón es una superposición del fotón pura electromagnética (que interactúa solamente con cargas eléctricas) y vector mesón.
El fotón como un bosón gauge
El campo electromagnético puede ser entendido como uncampo de calibre, es decir, como un campo que resulta de requerir que una simetría gauge sostiene de forma independiente en cada posición en espacio tiempo. Para el el campo electromagnético, esta simetría de calibre es elabelianoU (1) simetría de unnúmero complejo, que refleja la capacidad de variar lafase de un número complejo sin afectarobservables oreal de funciones con valoresderivados de éste, tales como laenergíao lafunción de Lagrange.
Los cuantos de un campo gauge abeliano debe ser, sin carga bosones sin masa, siempre que la simetría no se rompe; por lo tanto, el fotón se prevé que sea sin masa, y tener cero carga eléctrica y spin entero. La forma particular de la interacción electromagnética especifica que el fotón debe tener giro ± 1; por lo tanto, su helicidad debe ser 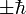 . Estos dos componentes de spin corresponden a los conceptos clásicos de la luz polarizada circularmente a derechas y zurdo. Sin embargo, los transitorios fotones virtuales de la electrodinámica cuántica también pueden adoptar estados de polarización no físicos.
. Estos dos componentes de spin corresponden a los conceptos clásicos de la luz polarizada circularmente a derechas y zurdo. Sin embargo, los transitorios fotones virtuales de la electrodinámica cuántica también pueden adoptar estados de polarización no físicos.
En el vigente modelo estándar de la física, el fotón es uno de los cuatro bosones gauge de la interacción electrodébil; la otros tres se designan W + , W - y Z 0 y son responsables de la interacción débil. diferencia de los fotones, estos bosones gauge tienen masa, debido a un mecanismo que rompe su SU (2) simetría gauge. La unificación del fotón con bosones gauge W y Z en la interacción electrodébil fue realizada por Sheldon Glashow, Abdus Salam y Steven Weinberg, para el que fueron otorgados los 1.979 Premio Nobel de Física. físicos siguen la hipótesis de las grandes teorías unificadas que conectan estos cuatro bosones gauge con los ocho bosones gauge gluones de la cromodinámica cuántica; Sin embargo, las predicciones clave de estas teorías, tales como la desintegración de protones, no se han observado experimentalmente.
Las contribuciones a la masa de un sistema
La energía de un sistema que emite un fotón es disminuido por la energía 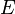 del fotón como se mide en el marco resto del sistema emisor de luz, que puede resultar en una reducción de la masa en la cantidad
del fotón como se mide en el marco resto del sistema emisor de luz, que puede resultar en una reducción de la masa en la cantidad 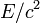 . mismo modo, la masa de un sistema que absorbe un fotón es el aumento en la cantidad correspondiente. Como aplicación, el balance de energía de las reacciones nucleares que involucran fotones se escribe comúnmente en términos de las masas de los núcleos implicados, y los términos de la forma
. mismo modo, la masa de un sistema que absorbe un fotón es el aumento en la cantidad correspondiente. Como aplicación, el balance de energía de las reacciones nucleares que involucran fotones se escribe comúnmente en términos de las masas de los núcleos implicados, y los términos de la forma 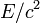 de los fotones gamma (y para otras energías pertinentes, tales como la energía de retroceso de núcleos).
de los fotones gamma (y para otras energías pertinentes, tales como la energía de retroceso de núcleos).
Este concepto se aplica en las predicciones clave de la electrodinámica cuántica (QED, véase más arriba). En esta teoría, la masa de electrones (o, más generalmente, leptones) se modifica mediante la inclusión de las contribuciones de masas de fotones virtuales, en una técnica conocida como renormalización . Tales "correcciones radiativas" contribuyen a una serie de predicciones de QED, como el momento magnético dipolar de leptones, el cambio de Cordero, y el estructura hiperfina de pares de leptones consolidados, como los muonio y positronium.
Desde fotones contribuyen al tensor de tensión-energía, ejercen una atracción gravitatoria sobre otros objetos, de acuerdo con la teoría de la relatividad general . Por el contrario, los fotones son ellos mismos afectados por la gravedad; sus trayectorias normalmente rectas pueden doblarse por deformado el espacio-tiempo, como en las lentes gravitacionales, y sus frecuencias pueden reducirse moviendo a un mayor potencial gravitatoria, como en el experimento de Pound-Rebka. Sin embargo, estos efectos no son específicos de fotones; exactamente los mismos efectos serían predichas para clásicos ondas electromagnéticas .
Los fotones de la materia
Cualquier "explicación" de cómo los fotones viajan a través de la materia tiene que explicar por qué diferentes disposiciones de la materia son transparentes u opacos en diferentes longitudes de onda (la luz a través de carbono como diamante o no, como el grafito) y por qué los fotones individuales se comportan de la misma manera como los grupos grandes. Las explicaciones que invocan 'absorción' y 're-emisión "tienen que dar una explicación de la direccionalidad de los fotones (difracción, reflexión) y, además de explicar cómo enredado pares de fotones pueden viajar a través de materia sin colapsar su estado cuántico.
La explicación más simple es que la luz que viaja a través de la materia transparente lo hace a una velocidad menor que c , la velocidad de la luz en el vacío. Además, la luz puede también someterse dispersión y absorción. Hay circunstancias en las que la transferencia de calor a través de un material es mayormente radiativo, que implica la emisión y absorción de fotones dentro de ella. Un ejemplo sería en el núcleo de la dom La energía puede tomar alrededor de un millón de años en llegar a la superficie. Sin embargo, este fenómeno es distinta de la radiación dispersada de forma difusa que pasa a través de la materia, ya que implica equilibrio local entre la radiación y la temperatura. Por lo tanto, el tiempo es el tiempo que tarda la energía para ser no transferido, los fotones mismos. Una vez en el espacio abierto, un fotón desde el Sol tarda sólo 8,3 minutos para llegar a la Tierra. El factor por el que la velocidad de la luz se reduce en un material se denomina el índice de refracción del material. En una imagen de la onda clásica, la desaceleración se explica por la luz que induce la polarización eléctrica en la materia, la materia polarizada que irradia luz nueva, y la nueva luz que interfiere con la onda de luz original para formar una onda retrasada. En una imagen de las partículas, la desaceleración en lugar puede ser descrito como una mezcla del fotón con excitación cuántica de la materia ( cuasi-partículas como fonones y excitones) para formar un polariton; este polariton tiene un distinto de cero masa efectiva, lo que significa que no puede viajar a c .
Alternativamente, los fotones pueden ser vistos como siempre viaja a c , incluso en la materia, pero tienen su desfasada (en diferido o avanzado) en interacción con las dispersa atómicas: modifica su longitud de onda y el impulso, pero no la velocidad. Una onda de luz formado por estos fotones no viajan más lento que la velocidad de la luz. En este punto de vista los fotones son "vacía", y se encuentran dispersos y la fase cambiaron, mientras que en la vista del párrafo anterior los fotones son "vestidas" por su interacción con la materia, y se mueven sin dispersión o cambio de fase, pero a una velocidad menor .
Luz de diferentes frecuencias puede viajar a través de la materia a diferentes velocidades; se llama dispersión. En algunos casos, puede dar lugar a velocidades extremadamente lentas de la luz en la materia. Los efectos de las interacciones de fotones con otras cuasipartículas pueden ser observados directamente en la dispersión Raman y Dispersión de Brillouin.
Los fotones también pueden ser absorbidos por los núcleos, átomos o moléculas, provocando transiciones entre su los niveles de energía. Un ejemplo clásico es la transición molecular de la retina C 20 H 28 O, que es responsable de la visión, como descubierto en 1958 por el premio Nobel bioquímico George Wald y compañeros de trabajo. La absorción provoca una cis-trans isomerización que, en combinación con otros tales transiciones, se transduce en impulsos nerviosos. La absorción de fotones puede incluso romper enlaces químicos, como en la fotodisociación de cloro ; este es el tema de la fotoquímica. Análogamente, los rayos gamma pueden en algunas circunstancias disociar los núcleos atómicos en un proceso llamado fotodesintegración.
Aplicaciones tecnológicas
Los fotones tienen muchas aplicaciones en la tecnología. Estos ejemplos son elegidos para ilustrar las aplicaciones de los fotones en sí , en lugar de dispositivos ópticos generales tales como lentes, etc., que podrían operar bajo una teoría clásica de la luz. El láser es una aplicación muy importante y se discute anteriormente bajo emisión estimulada.
Fotones individuales pueden ser detectados por varios métodos. El clásico tubo fotomultiplicador explota el efecto fotoeléctrico: un aterrizaje de fotones en una placa de metal expulsa un electrón, iniciando una avalancha cada vez amplificar de electrones. chips de dispositivo de carga acoplada utilizan un efecto similar en semiconductores : un fotón incidente genera una carga en un microscópico condensador que puede ser detectado. Otros detectores tales como contadores Geiger utilizan la capacidad de los fotones para ionizar las moléculas de gas, causando un cambio detectable en la conductividad.
Fórmula de la energía de Planck es a menudo utilizado por los ingenieros y químicos en el diseño, tanto para calcular el cambio en la energía que resulta de una absorción de fotones y para predecir la frecuencia de la luz emitida por una energía dada transición. Por ejemplo, el espectro de emisión de unbombilla fluorescente puede diseñarse usando moléculas de gas con diferentes niveles de energía electrónica y el ajuste de la energía típica con la que un electrón golpea las moléculas de gas dentro de la bombilla.
es a menudo utilizado por los ingenieros y químicos en el diseño, tanto para calcular el cambio en la energía que resulta de una absorción de fotones y para predecir la frecuencia de la luz emitida por una energía dada transición. Por ejemplo, el espectro de emisión de unbombilla fluorescente puede diseñarse usando moléculas de gas con diferentes niveles de energía electrónica y el ajuste de la energía típica con la que un electrón golpea las moléculas de gas dentro de la bombilla.
Bajo ciertas condiciones, una transición energética puede ser excitado por "dos" fotones que individualmente serían insuficientes. Esto permite una mayor resolución microscopía, debido a que la muestra absorbe energía sólo en la región en la que dos haces de diferentes colores se superponen significativamente, lo que se puede hacer mucho más pequeño que el volumen de excitación de un único haz (ver excitación microscopía de dos fotones). Por otra parte, estos fotones causan menos daño a la muestra, ya que son de menor energía.
En algunos casos, dos transiciones de energía pueden ser acoplados de manera que, como un solo sistema absorbe un fotón, otro sistema cercanos "roba" su energía y re-emite un fotón de una frecuencia diferente. Esta es la base de la transferencia de energía por resonancia de fluorescencia, una técnica que se utiliza en la biología molecular para estudiar la interacción de adecuados proteínas .
Varios tipos diferentes de hardware generador de números aleatorios implican la detección de fotones individuales. En un ejemplo, para cada bit en la secuencia aleatoria que se va a producir, un fotón se envía a un divisor de haz. En tal situación, hay dos posibles resultados de la misma probabilidad. El resultado real se utiliza para determinar si el siguiente bit en la secuencia es "0" o "1".
Investigación reciente
Muchas investigaciones se han dedicado a las aplicaciones de los fotones en el campo de la óptica cuántica. Los fotones parecen bien adaptado a ser elementos de un extremadamente rápido ordenador cuántico , y el entrelazamiento cuántico de los fotones es un foco de la investigación. procesos ópticos no lineales son otra área de investigación activa, con temas tales como la absorción de dos fotones, la modulación de la auto-fase, Inestabilidad modulación y osciladores paramétricos ópticos. Sin embargo, tales procesos no requieren generalmente la suposición de fotones per se ; que a menudo pueden ser modelados mediante el tratamiento de los átomos como los osciladores no lineales. El proceso no lineal de conversión paramétrica abajo espontánea se utiliza a menudo para producir estados de fotón único. Finalmente, los fotones son esenciales en algunos aspectos de la comunicación óptica, especialmente para la criptografía cuántica.