
Georg Cantor
Antecedentes
SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . El patrocinio de los niños ayuda a los niños en el mundo en desarrollo para aprender también.
| Georg Cantor | |
|---|---|
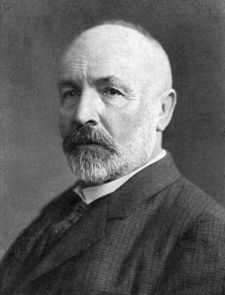 | |
| Nacido | Georg Ferdinand Ludwig Philipp Cantor 03 de marzo 1845 San Petersburgo , Imperio ruso |
| Murió | 06 de enero 1918 (72 años) Halle, Provincia de Sajonia, Imperio Alemán |
| Residencia | Imperio ruso (1845-1856), Imperio Alemán (1856-1918) |
| Nacionalidad | Alemán |
| Campos | Matemáticas |
| Instituciones | Universidad de Halle |
| Alma máter | ETH Zurich, Universidad de Berlín |
| Doctoral consejero | Ernst Kummer Karl Weierstrass |
| Los estudiantes de doctorado | Alfred Barneck |
| Conocido por | Teoría de conjuntos |
Georg Ferdinand Ludwig Philipp Cantor (pron .: / k æ n t ɔr / KAN -tor; alemán: [ɡeɔʁk fɛʁdinant luːtvɪç fɪlɪp kantɔʁ]; 03 de marzo [ OS 19 de febrero] 1845 - 6 de enero 1918) fue un Alemán matemático , más conocido como el inventor de la teoría de conjuntos , que se ha convertido en un teoría fundamental en matemáticas. Cantor estableció la importancia de uno-a-uno correspondencia entre los miembros de dos conjuntos, que se define infinito y conjuntos bien ordenada, y demostraron que los números reales son "más numerosos" que los números naturales . De hecho, el método de la prueba de este teorema de Cantor implica la existencia de un " infinito de infinitos ". Definió el cardinal y ordinal número y su aritmética. El trabajo de Cantor es de gran interés filosófico, un hecho del que era muy consciente.
Teoría de Cantor números transfinitos fue considerado originalmente como lo contrario a la intuición - incluso chocante - que encontró resistencia por parte de los contemporáneos matemáticos como Leopold Kronecker y Henri Poincaré y más tarde de Hermann Weyl y LEJ Brouwer, mientras que Ludwig Wittgenstein planteó objeciones filosóficas. Algunos Los teólogos cristianos (sobre todo neo-escolásticos) vio el trabajo de Cantor como un desafío a la singularidad de la infinidad absoluta en la naturaleza de Dios - en una ocasión equiparar la teoría de los números transfinitos con panteísmo - una proposición que Cantor rechazó enérgicamente. Las objeciones a su trabajo eran ocasionalmente feroz: Poincaré se refirió a las ideas de Cantor como una "grave enfermedad" infectar la disciplina de las matemáticas , y la oposición pública de Kronecker y ataques personales incluye la descripción de Cantor como un "charlatán científico", un "renegado" y un " corruptor de la juventud ". Kronecker incluso se opuso a las pruebas de Cantor que los números algebraicos son contables, y que los números trascendentales son incontables, los resultados ahora se incluye en un plan de estudios de matemáticas estándar. Escribir décadas después de la muerte de Cantor, Wittgenstein lamentó que la matemática está "montado hasta la médula con los modismos perniciosos de la teoría de conjuntos", que él calificó de "tonterías" que es "ridículo" y "malo". Episodios recurrentes de Cantor de depresión a partir de 1884 hasta el final de su vida ha sido atribuida a la actitud hostil de muchos de sus contemporáneos, aunque algunos han explicado estos episodios como manifestaciones probables de un trastorno bipolar.
La dura crítica ha ido acompañado de elogios posteriores. En 1904, la Real Sociedad otorgó Cantor su Medalla Sylvester, el más alto honor que puede conferir para el trabajo en matemáticas. Se ha sugerido que Cantor creía que su teoría de los números transfinitos se había comunicado con él por Dios. David Hilbert lo defendió de sus críticos al famoso declarando: "Nadie nos podrá, por expulsión del paraíso que Cantor ha creado."
Vida
Juventud y estudios

Cantor nació en 1845 en la colonia comerciante occidental en San Petersburgo , Rusia , y se crió en la ciudad hasta que tenía once años. Georg, el mayor de seis hijos, fue considerado como un destacado violinista . Su abuelo Franz Böhm (1788-1846) (el violinista El hermano de Joseph Böhm) fue el conocido músico y el solista en el imperio ruso en una orquesta imperial. El padre de Cantor había sido miembro de la San Petersburgo bolsa de valores; cuando se enfermó, la familia se trasladó a Alemania en 1856, primero en Wiesbaden después a Frankfurt , en busca de los inviernos más suaves que las de San Petersburgo. En 1860, Cantor se graduó con honores en la Realschule en Darmstadt; sus excepcionales habilidades en matemáticas, trigonometría , en particular, se observaron. En 1862, entró en el Cantor Universidad de Zürich. Después de recibir una importante herencia a la muerte de su padre en 1863, Cantor movió sus estudios a la Universidad de Berlín, asistir a conferencias a cargo de Leopold Kronecker, Karl Weierstrass y Ernst Kummer. Pasó el verano de 1866 en el Universidad de Göttingen, entonces y después, un centro para la investigación matemática.
Docente e investigadora
En 1867, Cantor terminó su disertación, en la teoría de números, en la Universidad de Berlín. Después de enseñar brevemente en una escuela de Berlín niñas, Cantor tomó una posición en el Universidad de Halle, donde pasó toda su carrera. Fue galardonado con el requisito habilitación para su tesis, también en la teoría de números, que presentó en 1869, tras su nombramiento en Halle.
En 1874, se casó con Cantor Vally Guttmann. Tuvieron seis hijos, el último (Rudolph) nacidos en 1886. Cantor fue capaz de mantener a una familia a pesar pago académico modesta, gracias a la herencia de su padre. Durante su luna de miel en el Montañas de Harz, Cantor pasó mucho tiempo en discusiones matemáticas con Richard Dedekind, a quien había conocido dos años antes, mientras que en Suiza vacaciones.
Cantor fue promovido a Profesor Extraordinario en 1872 e hizo profesor titular en 1879. Para alcanzar este último rango a la edad de 34 fue un logro notable, pero Cantor desea un cátedra en una universidad más prestigiosa, en particular, en Berlín, en ese momento la principal universidad alemana. Sin embargo, su trabajo se encontró demasiada oposición para que eso sea posible. Kronecker, que dirigió matemáticas en Berlín hasta su muerte en 1891, se convirtió cada vez más incómodo con la perspectiva de tener Cantor como un colega, le percibe como un "corruptor de la juventud" para la enseñanza de sus ideas a una generación más joven de los matemáticos. Peor aún, Kronecker, una figura bien establecida dentro de la comunidad matemática y ex profesor de Cantor, no estuvo de acuerdo fundamentalmente con la idea central de la obra de Cantor. Kronecker, ahora visto como uno de los fundadores de la punto de vista constructivo en las matemáticas, no le gustaba mucho de la teoría de conjuntos de Cantor, ya que afirmó la existencia de conjuntos que satisfacen ciertas propiedades, sin dar ejemplos específicos de grupos cuyos miembros, efectivamente satisfacer esas propiedades. Cantor llegó a creer que la postura de Kronecker haría imposible para él nunca para dejar Halle.
En 1881, Halle colega de Cantor Eduard Heine murió, creando una silla vacía. Halle aceptó la sugerencia de Cantor que se ofrecerá a los Dedekind, Heinrich M. Weber y Franz Mertens, en ese orden, pero cada declinó la silla después de haber sido ofrecido. Friedrich Wangerin fue finalmente nombrado, pero que queda muy Cantor.
En 1882, la correspondencia matemática entre Cantor y Dedekind llegó a su fin, al parecer como consecuencia de la disminución de Dedekind de la cátedra en Halle. Cantor también comenzó otra correspondencia importante, con Gösta Mittag-Leffler en Suecia, y pronto comenzó a publicar en el diario de Mittag-Leffler Acta Mathematica. Pero en 1885, Mittag-Leffler estaba preocupado por la naturaleza filosófica y nueva terminología en un documento Cantor había presentado al Acta. Pidió Cantor de retirar el papel de Acta mientras estaba en la prueba, escribiendo que era "... unos cien años antes de tiempo." Cantor accedió, pero luego redujo su relación y correspondencia con Mittag-Leffler, escrito a un tercero:
Tenía Mittag-Leffler tenía su manera, tendría que esperar hasta el año 1984, que para mí parecía demasiado grande una demanda! ... Pero, por supuesto, yo nunca quiero saber nada más sobre Acta Mathematica.
Cantor sufrió su primer ataque conocido de la depresión en 1884. La crítica de su trabajo pesado en su mente: cada uno de los cincuenta y dos cartas que escribió a Mittag-Leffler en 1884 mencionó Kronecker. Un pasaje de una de estas cartas es revelador de los daños a la auto-confianza de Cantor:
... No sé cuando voy a volver a la continuación de mi trabajo científico. Por el momento no puedo hacer absolutamente nada con él, y me limitaré a lo más necesario deber de mis conferencias; cuánto más feliz que habría de ser científicamente activo, si yo tuviera la frescura mental necesaria.
Esta crisis le llevó a aplicar para dar conferencias sobre filosofía en lugar de las matemáticas. También comenzó un intenso estudio de Pensar la literatura isabelina no podría ser evidencia de que Francis Bacon escribió las obras atribuidas a Shakespeare (ver Cuestión de la autoría de Shakespeare); esta última instancia resultó en dos folletos, publicado en 1896 y 1897.
Cantor se recuperó poco después, y posteriormente hizo contribuciones más importantes, incluyendo su famoso argumento diagonal y teorema. Sin embargo, nunca volvió a alcanzar el alto nivel de sus notables trabajos de 1874-1884. Con el tiempo se buscó, y logró, una reconciliación con Kronecker. Sin embargo, los desacuerdos filosóficos y dificultades que los dividen persistieron.
En 1890, Cantor fue instrumental en la fundación de la Deutsche Mathematiker-Vereinigung y presidió su primera reunión en Halle en 1891, donde por primera vez presentó su argumento diagonal; su reputación era lo suficientemente fuerte, a pesar de la oposición de Kronecker a su trabajo, para asegurar que fue elegido como el primer presidente de esta sociedad. Dejando a un lado la animosidad Kronecker había mostrado hacia él, Cantor lo invitó a dirigirse a la reunión, pero Kronecker no pudo hacerlo porque su esposa estaba muriendo de las heridas sufridas en un accidente de esquí en el momento.
Años de retraso
Después de 1884 la hospitalización de Cantor, no hay constancia de que estaba en cualquier sanatorio de nuevo hasta 1899. Poco después de que la segunda hospitalización, el hijo menor de Cantor Rudolph murió repentinamente (mientras Cantor estaba dando una conferencia sobre sus puntos de vista sobre Teoría de Bacon y William Shakespeare ), y esta tragedia drenado Cantor de gran parte de su pasión por las matemáticas. Cantor fue hospitalizado de nuevo en 1903. Un año más tarde, él se enfureció y agitado por un documento presentado por Julius König en la Tercera Congreso Internacional de Matemáticos. En el documento se intentó demostrar que los principios básicos de la teoría de conjuntos transfinitos eran falsas. (Konig es ahora recordado como haber sólo señalaron que algunos grupos no pueden estar bien ordenadas, en desacuerdo con Cantor.) Dado que el documento había sido leído delante de sus hijas y sus colegas, Cantor percibe a sí mismo como de haber sido humillado públicamente. Aunque Ernst Zermelo demostró menos de un día después de que la prueba de König había fracasado, Cantor permanecieron desconcierta, ni siquiera momentáneamente cuestionar a Dios. Cantor sufrió de depresión crónica por el resto de su vida, por lo que fue excluido de la docencia en varias ocasiones y en varias ocasiones limita en varios sanatorios. Los acontecimientos de 1904 precedidas de una serie de hospitalizaciones a intervalos de dos o tres años. No abandonó las matemáticas por completo, sin embargo, dar una conferencia sobre las paradojas de la teoría de conjuntos ( Paradoja de Burali-Forti, Paradoja de Cantor, y La paradoja de Russell) a una reunión de la Deutsche Mathematiker-Vereinigung en 1903, y participar en el Congreso Internacional de Matemáticos en Heidelberg en 1904.
En 1911, Cantor fue uno de los distinguidos académicos extranjeros invitados a asistir al 500 aniversario de la fundación de la Universidad de St. Andrews en Escocia . Cantor asistió, con la esperanza de conocer a Bertrand Russell , cuya reciente publicación Principia Mathematica citó repetidamente el trabajo de Cantor, pero esto no ocurrió. Al año siguiente, St. Andrews concedió Cantor un doctor honoris causa, pero la enfermedad impidió que recibiera el grado en persona.
Cantor se retiró en 1913, vive en la pobreza y que sufren de desnutrición durante la Primera Guerra Mundial . La celebración pública de su cumpleaños número 70 fue cancelada debido a la guerra. Murió el 6 de enero de 1918 en el sanatorio donde había pasado el último año de su vida.
Trabajo matemático
El trabajo de Cantor entre 1874 y 1884 es el origen de la teoría de conjuntos . Antes de este trabajo, el concepto de un conjunto fue bastante elemental que había sido utilizado de forma implícita desde los inicios de las matemáticas, que se remonta a las ideas de Aristóteles . Nadie se había dado cuenta de que la teoría de conjuntos tenía ningún contenido no trivial. Antes de Cantor, sólo había conjuntos finitos (que son fáciles de entender) y "el infinito" (que se considera un tema para filosófica, más que matemática, la discusión). Por demostrando que hay (infinitamente) muchos tamaños posibles para los conjuntos infinitos, Cantor estableció que la teoría de conjuntos no era trivial, y que necesitan ser estudiados. La teoría de conjuntos ha pasado a desempeñar el papel de un teoría fundacional en la matemática moderna, en el sentido de que interpreta proposiciones sobre objetos matemáticos (por ejemplo, números y funciones) de todas las áreas tradicionales de las matemáticas (como álgebra , análisis y topología ) en una sola teoría, y proporciona un conjunto estándar de axiomas para probar o refutar ellos. Los conceptos básicos de la teoría de conjuntos ahora se utilizan en toda la matemática.
En uno de sus primeros papeles, Cantor demostró que el conjunto de los números reales es "más numerosos" que el conjunto de los números naturales ; esto demuestra, por primera vez, que existen conjuntos infinitos de diferente tamaños. También fue el primero en apreciar la importancia de uno-a-uno correspondencia (en adelante denotados "correspondencia 1-a-1") en la teoría de conjuntos. Él utilizó este concepto para definir finito y conjuntos infinitos, subdividiendo la última en conjuntos numerables (o infinito numerable) y conjuntos numerables (conjuntos infinitos no numerable).
Cantor desarrolló conceptos importantes en la topología y su relación con cardinalidad. Por ejemplo, mostró que el Conjunto de Cantor es denso en ninguna parte, pero tiene la misma cardinalidad que el conjunto de todos los números reales, mientras que los racionales son denso en todas partes, pero numerable.
Cantor introdujo construcciones fundamentales en la teoría de conjuntos, como el conjunto potencia de un conjunto A, que es el conjunto de todos los posibles subconjuntos de A. Más tarde se demostró que el tamaño del conjunto potencia de A es estrictamente mayor que el tamaño de A, aun cuando A es un conjunto infinito; este resultado pronto se hizo conocido como El teorema de Cantor. Cantor desarrolló toda una teoría y aritmética de conjuntos infinitos, llamados cardenales y ordinales , que se extendió la aritmética de los números naturales. Su notación para los números cardinales era la letra hebrea  ( aleph) con un subíndice número natural; para los ordinales empleó la letra griega ω ( omega). Esta notación se encuentra todavía en uso hoy en día.
( aleph) con un subíndice número natural; para los ordinales empleó la letra griega ω ( omega). Esta notación se encuentra todavía en uso hoy en día.
La Hipótesis del continuo, introducida por Cantor, fue presentado por David Hilbert como el primero de su veintitrés problemas abiertos en su famoso discurso en el 1900 Congreso Internacional de Matemáticos en París . El trabajo de Cantor también atrajo la atención favorable allá encomio célebre de Hilbert. El filósofo estadounidense Charles Sanders Peirce elogió la teoría de conjuntos de Cantor, y, a raíz de conferencias públicas entregadas por Cantor en el primer Congreso Internacional de Matemáticos celebrado en Zurich en 1897, Hurwitz y Hadamard también tanto expresó su admiración. En ese Congreso, Cantor renovó su amistad y correspondencia con Dedekind. A partir de 1905, Cantor se correspondía con su admirador británico y traductor Philip Jourdain sobre la historia de la teoría de conjuntos y en las ideas religiosas de Cantor. Esto fue publicado más tarde, al igual que varios de sus trabajos expositivos.
Número teoría, series trigonométricas y ordinales
Diez primeros trabajos de Cantor estaban en la teoría de números , su tema de tesis. A sugerencia de Eduard Heine, el profesor en Halle, Cantor se volvió hacia el análisis . Heine propone que Cantor resolver un problema abierto que había eludido Dirichlet, Lipschitz, Bernhard Riemann , y el propio Heine: la unicidad de la representación de una función por series trigonométricas. Cantor resolvió este difícil problema en 1869. Fue mientras trabajaba en este problema que descubrió ordinales transfinitos, que se produjo como índices n en el n º derivada conjunto S n de un conjunto S de ceros de una serie trigonométrica. Dada una f series trigonométricas (x) con S como su conjunto de ceros, Cantor había descubierto un procedimiento que produjo otra serie trigonométrica que tenía S 1 como su conjunto de ceros, donde S 1 es el conjunto de limitar los puntos de S. Si S k + 1 es el conjunto de puntos límite de S k, entonces él podría construir una serie trigonométricas cuyos ceros son S k + 1. Debido a que los conjuntos S k estaban cerrados, que contenían su Puntos límite, y la intersección de la secuencia decreciente infinita de conjuntos S, S 1, S 2, S 3, ... forman un conjunto límite, que ahora llamaríamos S ω, y luego se dio cuenta de que S ω también tendría tener un conjunto de puntos S límite ω + 1, y así sucesivamente. Tenía ejemplos que pasaron para siempre, y aquí fue una sucesión infinita de origen natural de los números infinitos ω, ω + 1, ω + 2, ...
Entre 1870 y 1872, Cantor publicó más artículos sobre series trigonométricas, y también un documento que define los números irracionales como secuencias convergentes de números racionales . Dedekind, Cantor quien se hizo amigo en 1872, citó este documento más adelante ese año, en el documento donde por primera vez se propuso su célebre definición de los números reales por Cortes de Dedekind. Si bien la ampliación de la noción de número por medio de su revolucionario concepto de cardinalidad infinita, Cantor fue paradójicamente opuesto a las teorías de la infinitesimales de sus contemporáneos Otto Stolz y Paul du Bois-Reymond, describiéndolos como tanto "una abominación" y "un bacilo del cólera de las matemáticas". Cantor también publicó una "prueba" errónea de la inconsistencia de los infinitesimales.
Teoría de conjuntos

El comienzo de la teoría de conjuntos como una rama de las matemáticas es a menudo marcada por la publicación de 1874 el artículo de Cantor, "Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen" ("en una propiedad de la Colección de todos los números reales algebraicos"). Este artículo fue la primera en ofrecer una prueba rigurosa de que había más de un tipo de infinito. Anteriormente, todos los conjuntos infinitos habían asumido implícitamente que equinumerous (es decir, de "el mismo tamaño" o que tengan el mismo número de elementos). Cantor demostró que el conjunto de números reales y la colección de positivos enteros no son equinumerous. En otras palabras, los números reales no son contable. Su prueba es más complejo que el más elegante argumento diagonal, que ha dado en 1891. El artículo de Cantor también contiene un nuevo método de construcción números trascendentes. Números trascendentes se construyeron por primera vez por Joseph Liouville en 1844.
Cantor estableció esos resultados utilizando dos construcciones. Su primera construcción muestra cómo escribir la verdadera números algebraicos como una secuencia a 1, a 2, a 3, .... En otras palabras, los números algebraicos reales son numerables. Cantor comienza su segunda obra con cualquier secuencia de números reales. Usando esta secuencia, construye intervalos anidados cuya intersección contiene un número real no en la secuencia. Dado que cada secuencia de números reales se puede utilizar para construir un real no en la secuencia, los números reales no se pueden escribir como una secuencia - es decir, los números reales no son contables. Mediante la aplicación de su construcción a la secuencia de números algebraicos reales, Cantor produce un número trascendental. Cantor señala que sus construcciones resultan más - a saber, que proporcionan una nueva demostración del teorema de Liouville: Cada intervalo contiene infinitos números trascendentales. Próximo artículo de Cantor contiene una construcción que demuestra el conjunto de números trascendentales tiene el mismo "poder" (ver más abajo) como el conjunto de los números reales.
Entre 1879 y 1884, Cantor publicó una serie de seis artículos en Mathematische Annalen que juntos forman una introducción a su teoría de conjuntos. Al mismo tiempo, hubo una creciente oposición a las ideas de Cantor, dirigido por Kronecker, que admitió conceptos matemáticos sólo si podían ser construidos en un número finito de pasos de los números naturales, que él tomó indicarse en forma intuitiva. Para Kronecker, la jerarquía de infinitos de Cantor era inadmisible, ya aceptar el concepto de infinito actual abriría la puerta a las paradojas que desafían la validez de las matemáticas en su conjunto. Cantor también introdujo el Cantor establece durante este período.
El quinto artículo de esta serie, "Grundlagen einer allgemeinen Mannigfaltigkeitslehre" ("Fundamentos de una teoría general de Áridos"), publicado en 1883, fue el más importante de los seis y también fue publicado como un independiente monografía. Contenía la respuesta de Cantor a sus críticos y mostró cómo la números transfinitos eran una extensión sistemática de los números naturales. Comienza por definir conjuntos bien ordenados. Los números ordinales se introducen entonces como los tipos de órdenes de conjuntos bien ordenados. Cantor define entonces la suma y la multiplicación del cardenal y los números ordinales. En 1885, Cantor extendió su teoría de tipos de órdenes para que los números ordinales simplemente se convirtieron en un caso especial de tipos de órdenes.
En 1891, publicó un documento con su elegante "argumento diagonal" de la existencia de un conjunto no numerable. Aplicó la misma idea de probar El teorema de Cantor: el cardinalidad del conjunto potencia de un conjunto A es estrictamente mayor que la cardinalidad de A. Esto estableció la riqueza de la jerarquía de los conjuntos infinitos, y del cardenal y aritmética ordinal que Cantor había definido. Su argumento es fundamental en la solución de la Problema de la parada y la prueba de Primer teorema de incompletitud de Gödel. Cantor escribió sobre la conjetura de Goldbach en 1894.
En 1895 y 1897, Cantor publicó un artículo de dos partes en Mathematische Annalen bajo Dirección editorial de Felix Klein; estos fueron sus últimos papeles importantes en la teoría de conjuntos. El primer artículo comienza por definir conjunto, subconjunto , etc., de manera que serían en buena medida aceptable ahora. El cardenal y la aritmética ordinal son revisados. Cantor quería que el segundo documento para incluir una prueba de la hipótesis del continuo, pero tuvo que conformarse con expositing su teoría de la conjuntos y números ordinales bien ordenada. Cantor intenta demostrar que si A y B son conjuntos con un equivalente a un subconjunto de B y B equivalente a un subconjunto de A, entonces A y B son equivalentes. Ernst Schröder había declarado este teorema un poco antes, pero su prueba, así como Cantor, era errónea. Felix Bernstein suministra una prueba de razón en su tesis doctoral 1898; de ahí el nombre Teorema de Cantor-Bernstein-Schroeder.
Uno-a-uno

1874 papel Crelle de Cantor fue el primero en invocar la noción de un 1-a-1 correspondencia, aunque él no utilizó esa frase. Él entonces comenzó a buscar una correspondencia 1 a 1 entre los puntos de la cuadrado de la unidad y los puntos de una unidad segmento de línea. En una carta de 1877 a Dedekind, Cantor demostró una medida de resultado más fuerte: para cualquier entero positivo n, existe una correspondencia 1-a-1 entre los puntos en el segmento de línea de la unidad y todos los puntos en una n espacio dimensional. Acerca de este descubrimiento Cantor famosamente escribió a Dedekind: "Je le vois, mais je ne le crois pas!" ("Yo lo veo, pero no me lo creo!") El resultado que se encuentra tan sorprendente tiene implicaciones para la geometría y la noción de dimensión.
En 1878, Cantor presentó otro papel para Diario de Crelle, en la que se define con precisión el concepto de una correspondencia 1-a-1, e introdujo el concepto de " poder "(un término que tomó de Jakob Steiner) o "equivalencia" de los conjuntos: dos conjuntos son equivalentes (tienen la misma potencia) si existe una correspondencia 1 a 1 entre ellos. Cantor definido conjuntos numerables (o conjuntos numerables) como conjuntos que se pueden poner en una correspondencia 1-a-1 con los números naturales , y demostraron que los números racionales son numerables. También demostró que n-dimensional espacio euclidiano R n tiene la misma potencia que el número real de R, al igual que un infinito numerable producto de copias de R. Mientras que él hizo uso gratuito de rendición como un concepto, él no escribió la palabra "contable" hasta 1883. Cantor también discutió su pensamiento acerca de dimensión, haciendo hincapié en que su mapeo entre la intervalo de la unidad y el cuadrado de la unidad no fue un uno continuo.
En este trabajo se disgustó Kronecker, y Cantor quería retirará; Sin embargo, Dedekind lo convenció de no hacerlo y Weierstrass apoyó su publicación. Sin embargo, Cantor nunca volvió a presentar nada para Crelle.
Hipótesis del continuo
Cantor fue el primero en formular lo que más tarde llegó a ser conocido como el hipótesis del continuo o CH: no existe ningún conjunto cuya potencia es mayor que la de los naturales y menos que la de los reales (o equivalentemente, la cardinalidad de los reales es exactamente aleph-uno, en lugar de sólo al menos aleph-uno). Cantor creía que la hipótesis del continuo es cierto y juzgado por muchos años para demostrar que, en vano. Su incapacidad para probar la hipótesis del continuo le causaba una ansiedad considerable.
La dificultad Cantor tenía en probar la hipótesis del continuo ha sido subrayada por los acontecimientos posteriores en el campo de las matemáticas: un resultado 1940 por Gödel y un uno por 1963 Paul Cohen juntos implica que la hipótesis del continuo puede ser probada ni refutada mediante norma Axiomas de Zermelo-Fraenkel, más el axioma de elección (la combinación denominado "ZFC").
Paradojas de la teoría de conjuntos
Los debates de la teoría de conjuntos paradojas comenzaron a aparecer a finales del siglo XIX. Algunos de estos problemas fundamentales implícitas con programa de la teoría de conjuntos de Cantor. En un documento de 1897 sobre un tema relacionado, Cesare Burali-Forti establece la primera paradoja, la Burali-Forti paradoja: el número ordinal del conjunto de todos los ordinales debe ser un ordinal y esto lleva a una contradicción. Cantor descubrió esta paradoja en 1895, y lo describió en una carta de 1896 a Hilbert . La crítica montado en el punto en el que Cantor lanzó contra-argumentos en 1903, destinada a defender los principios básicos de su teoría de conjuntos.
En 1899, Cantor descubrió su epónimo paradoja: ¿cuál es el número cardinal del conjunto de todos los conjuntos? Es evidente que debe ser el mayor posible cardenal. Sin embargo, para cualquier conjunto A, el número cardinal del conjunto potencia de A es estrictamente mayor que el número cardinal de A (este hecho es ahora conocido como El teorema de Cantor). Esta paradoja, junto con Burali-Forti de, llevó Cantor para formular un concepto llamado limitación de tamaño, según la cual la colección de todos los ordinales, o de todos los conjuntos, fue una "multiplicidad inconsistente" que era "demasiado grande" como un conjunto. Dichas colecciones más tarde se conoció como clases apropiadas.
Un punto de vista común entre los matemáticos es que estas paradojas, junto con La paradoja de Russell, demostrar que no es posible tomar un "ingenuo", o no axiomática, enfoque de la teoría de conjuntos sin poner en riesgo la contradicción, y es cierto que se encontraban entre las motivaciones para Zermelo y otros para producir axiomatizaciones de la teoría de conjuntos. Otros observan, sin embargo, que las paradojas no obtienen en una vista informal motivado por la jerarquía iterativo, que se puede ver como la explicación de la idea de la limitación de tamaño. Algunos también se preguntan si la Formulación de Frege la teoría de conjuntos ingenua (que era el sistema directamente refutada por la paradoja de Russell) es realmente una interpretación fiel de la concepción cantoriana.
La filosofía, la religión, y las matemáticas de Cantor
El concepto de la existencia de una infinito actual fue una importante preocupación compartida dentro de los reinos de las matemáticas, la filosofía y la religión. La preservación de la la ortodoxia de la relación entre Dios y las matemáticas, aunque no de la misma forma como se llevó a cabo por sus críticos, fue durante mucho tiempo una preocupación de Cantor. Se dirigió directamente esta intersección entre estas disciplinas en la introducción a su Mannigfaltigkeitslehre allgemeinen einer Grundlagen, donde destacó la conexión entre su visión de lo infinito y lo filosófico. Para Cantor, sus puntos de vista matemáticos estaban intrínsecamente ligados a sus implicaciones filosóficas y teológicas - él identificó el Absoluto Infinito con Dios , y él consideran su trabajo sobre los números transfinitos que se han comunicado directamente a él por Dios, que había elegido Cantor revelarlos al mundo.
Debate entre los matemáticos surgió a partir de puntos de vista opuestos en la filosofía de las matemáticas en relación con la naturaleza del infinito real. Algunos sostenían la opinión de que el infinito era una abstracción que no era matemáticamente legítimo, y negó su existencia. Los matemáticos a partir de tres grandes escuelas de pensamiento ( constructivismo y sus dos vástagos, intuicionismo y finitismo) se opuso a las teorías de Cantor en este asunto. Para los constructivistas como Kronecker, este rechazo de infinito actual deriva de desacuerdo fundamental con la idea de que pruebas no constructivos como argumento diagonal de Cantor son prueba suficiente de que algo existe, sostiene en cambio que Se requieren pruebas constructivas. El intuicionismo también rechaza la idea de que el infinito real es una expresión de cualquier tipo de realidad, pero llegar a la decisión a través de una ruta diferente que el constructivismo. En primer lugar, el argumento de Cantor se basa en la lógica para demostrar la existencia de los números transfinitos como una entidad matemática real, mientras que los intuicionistas sostienen que las entidades matemáticas no pueden ser reducidas a proposiciones lógicas, originarios en su lugar en las intuiciones de la mente. En segundo lugar, la noción de infinito como una expresión de la realidad es en sí denegado en el intuicionismo, ya que la mente humana no puede construir de manera intuitiva un conjunto infinito. Matemáticos tales como Brouwer y especialmente Poincaré adoptó un postura intuicionista contra el trabajo de Cantor. Citando las paradojas de la teoría de conjuntos como un ejemplo de su naturaleza fundamentalmente defectuoso, Poincaré sostuvo que "la mayor parte de las ideas de la teoría de conjuntos cantoriana debe ser desterrado de las matemáticas una vez por todas." Finalmente, Wittgenstein ataques 's eran finitista: él cree que el argumento diagonal de Cantor combinó la intensión de un conjunto de cardinal o números reales con su extensión, fusionando así el concepto de reglas para generar un conjunto con un juego real.
Algunos teólogos cristianos vieron el trabajo de Cantor como un desafío a la singularidad de la infinidad absoluta en la naturaleza de Dios. En particular, Pensadores neo-tomistas vieron la existencia de un infinito actual que consistía en algo que no sea Dios como poner en peligro "derecho exclusivo de Dios hasta el infinito supremo". Cantor creía firmemente que este punto de vista fue una mala interpretación de lo infinito, y estaba convencido de que la teoría de conjuntos podría ayudar a corregir este error:
... La especie transfinitos son apenas tanto a disposición de las intenciones del Creador y Su infinita absoluta serán igual que los números finitos.
Cantor también creía que su teoría de los números transfinitos iba en contra de los dos materialismo y determinismo - y se sorprendió cuando se dio cuenta de que él era el único miembro de la facultad en Halle que no tenían a creencias filosóficas deterministas.
En 1888, Cantor publicó su correspondencia con varios filósofos sobre las implicaciones filosóficas de su teoría de conjuntos. En un amplio intento por persuadir a otros pensadores y autoridades cristianas a adoptar su punto de vista, Cantor había mantenido correspondencia con filósofos cristianos como Tilman Pesch y Joseph Hontheim, así como teólogos como Cardenal Johannes Franzelin, que una vez respondió igualando la teoría de los números transfinitos con panteísmo. Cantor incluso envió una carta directamente a El Papa León XIII a sí mismo, y abordaron varios folletos con él.
La filosofía de Cantor sobre la naturaleza de los números le llevó a afirmar una creencia en la libertad de las matemáticas para postular y demostrar conceptos aparte del reino de los fenómenos físicos, como expresiones dentro de una realidad interna. Las únicas restricciones a este sistema metafísico son que todos los conceptos matemáticos deben estar desprovistos de contradicción interna, y que se derivan de las definiciones existentes, axiomas y teoremas. Esta creencia se resume en su famosa afirmación de que "la esencia de las matemáticas es su libertad." Estas ideas son paralelas a las de Edmund Husserl.
Mientras tanto, el propio Cantor era ferozmente opuesto a los infinitesimales, describiéndolos como tanto una "abominación" y "el bacilo del cólera de las matemáticas".
Papel de Cantor 1883 revela que él era muy consciente de laoposición a sus ideas fueron encontrando:
... Me doy cuenta de que en esta empresa me pongo en una cierta oposición a las opiniones ampliamente celebradas en relación con las matemáticas infinitas y opiniones a menudo defendió en la naturaleza de los números.
De ahí que dedica mucho espacio a justificar su trabajo anterior, afirmando que los conceptos matemáticos se pueden introducir libremente, siempre y cuando estén libres de contradicción y se define en términos de conceptos previamente aceptados. También cita a Aristóteles , Descartes, Berkeley, Leibniz y Bolzano en el infinito.
Ascendencia de Cantor

"Muy poco se sabe a ciencia cierta sobre el origen y la educación de George Woldemar Cantor". Abuelos paternos de Cantor eran de Copenhague , y huyeron a Rusia desde la interrupción de las guerras napoleónicas . Hay muy poca información directa sobre sus abuelos. Cantor fue a veces llamado judío en su vida, pero también ha sido diversamente llamado ruso, alemán y danés también.
Jakob Cantor, el abuelo de Cantor, dio a sus hijos cristianos nombres de santos. Además, varios de los parientes de su abuela estaban en la función pública zarista, que no daría la bienvenida a Judios, a menos que se convirtieron al cristianismo. El padre de Cantor, Georg Waldemar Cantor, fue educado en la misión Luterana en San Petersburgo, y de su correspondencia con su hijo muestra tanto de ellos como luteranos devotos. Su madre, Maria Anna Böhm, fue un austro-húngaro nacido en San Petersburgo y bautizada católica romana ; se convirtió al protestantismo en el matrimonio. Sin embargo, hay una carta del hermano de Louis Cantor a su madre, diciendo:
Mogen Wir zehnmal von Juden abstammen und ich im Princip noch für lo sehr Gleichberechtigung der Hebräer sein, im Leben sind socialen mir Christen lieber ...
En una carta escrita por Georg Cantor a Pablo Curtiembre en 1896 (Paul Curtiembre, Mémoires Scientifique 13 Correspondencia, Gauthier-Villars, París, 1934, p. 306), Cantor afirma que sus abuelos paternos eran miembros de la comunidad judía sefardí de Copenhague. Específicamente, Cantor afirma en la descripción de su padre: "Er ist aber en geboren Kopenhagen, von israelitischen Eltern, die der dortigen portugisischen Judengemeinde ..." ("Nació en Copenhague de los judíos (lit:" los padres de Israel ") de lo local comunidad portuguesa-judía ".) Además, gran tío materno de Cantor, un violinista húngaro Josef Böhm, ha sido descrito como judía, lo que puede implicar que la madre de Cantor fue al menos en parte descendiente de la comunidad judía de Hungría.
En una carta a Bertrand Russell, Cantor describió su ascendencia y la autopercepción de la siguiente manera:
Ni mi padre ni mi madre eran de sangre alemana, siendo el primero un danés, tener en Copenhague, mi madre de Hungar austríaco descension. Usted debe saber, señor, que yo no soy un habitual simplemente Germain , porque yo he nacido 03 de marzo 1845 en Saint Peterborough, capital de Rusia, pero me fui con mi padre y mi madre y sus hermanos y hermana, once años de edad en el año 1856 , en Alemania.
Historiografía
Hasta la década de 1970, las principales publicaciones académicas sobre Cantor había dos monografías breves Schönflies (1927) - en gran medida la correspondencia con Mittag-Leffler - y Fraenkel (1930). Ambos estaban en segunda y tercera mano; ninguno tuvo tanto en su vida personal. La brecha se llenó en gran medida por Eric Temple Bell Men of Mathematics (1937), que uno de los biógrafos modernos de Cantor describe como "quizás el libro moderno más leído en la historia de las matemáticas "; y como "uno de los peores". Campana presenta la relación de Cantor con su padre como Edipo, las diferencias de Cantor con Kronecker como una pelea entre dos Judios, y la locura de Cantor como la desesperación romántica sobre su fracaso para ganar la aceptación de sus matemáticas, y llena el cuadro con los estereotipos. Grattan-Guinness (1971) encontró que ninguna de estas afirmaciones fuera cierta, pero se puede encontrar en muchos libros del período de intervención, debido a la ausencia de cualquier otra narrativa. Hay otras leyendas, independientemente de Campana - incluyendo uno que etiqueta padre de Cantor un expósito, enviado a San Petersburgo por los padres desconocidos. Una crítica del libro de Bell está contenida en la biografía de Joseph Dauben.
