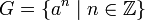Grupo (matemáticas)
Acerca de este escuelas selección Wikipedia
Organizar una selección Wikipedia para las escuelas en el mundo en desarrollo sin acceso a Internet era una iniciativa de SOS Children. Antes de decidir sobre el patrocinio de un niño, ¿por qué no aprender sobre diferentes obras de caridad de patrocinio primero ?

Un grupo es uno de los objetos fundamentales de estudio en el campo de las matemáticas conocida como álgebra abstracta . La rama del álgebra que estudia los grupos se llama la teoría de grupos . La teoría de grupos tiene amplias aplicaciones en las matemáticas, la ciencia y la ingeniería. Muchas estructuras algebraicas tales como campos y espacios vectoriales se pueden definir de forma concisa en cuanto a los grupos, y la teoría de grupos proporciona una herramienta importante para el estudio de la simetría , ya que las simetrías de cualquier objeto forman un grupo. Los grupos son por lo tanto abstracciones esenciales en ramas de la física que implican simetría principios, como la relatividad , la mecánica cuántica y la física de partículas . Además, su capacidad para representar geométricas transformaciones encuentra aplicaciones en la química , gráficos por ordenador, y otros campos.
| La teoría de grupos |
|---|
Nociones básicas
Homomorfismos de grupo
|
Grupos finitos
Clasificación de los finitos grupos simples
Grupos de Mathieu
Grupos Conway
Grupos Janko
Grupos Fischer
|
Grupos modulares
|
Topológica / Grupos de Lie
Infinito grupo de Lie dimensional
|
Grupos algebraicos |
Muchas estructuras investigadas en matemáticas resultan ser grupos. Estos incluyen sistemas conocidos de números, tales como: los números enteros , los números racionales , los números reales y los números complejos bajo la adición, así como los racionales no-cero, reales, y los números complejos bajo la multiplicación. Otros ejemplos importantes son: el grupo de los no singulares matrices bajo multiplicación, y el grupo de funciones invertibles bajo composición . La teoría de grupos permite que las propiedades de este tipo de estructuras que podrían investigarse en un entorno general.
Definición
Un grupo (G, *) es una establecer G con una operación binaria * que satisface los siguientes cuatro axiomas:
- Cierre: Para todo a, b en G, el resultado de un * b es también en G.
- Asociatividad : Para todo a, b y c en G, (a * b) * c = a * (b * c).
- Elemento de identidad: No existe un elemento e en G tal que para todo a en G, e * a = a * e = a.
- Elemento inverso: Para cada una en G, existe un elemento b en G tal que a * b = b * a = e, donde e es un elemento de identidad.
Algunos textos omiten el requisito explícito de cierre, desde el cierre del grupo de la definición de un operación binaria.
Usando la propiedad de elemento de identidad, se puede demostrar que un grupo tiene exactamente un elemento de identidad. Vea la demostración de abajo.
El inverso de un elemento a también puede demostrarse que es único, y por lo general se escribe un -1 (pero ver la notación abajo para grupos aditivamente escritos).
Un grupo (G, *) se denota a menudo simplemente G donde no hay ambigüedad en cuanto a lo que la operación es.
Ilustración de la definición

Un ejemplo explicará algunas de las propiedades de los grupos. Considere la posibilidad de un cuadrado . Estamos interesados en las simetrías de la plaza. Existen los siguientes tipos de simetrías:
- rotación alrededor de 90 °, 180 ° y 270 ° (sentido horario). Vamos a escribir estas simetrías como pudrición 90 °, 180 ° pudrirse ya la descomposición 270 °, respectivamente. Tenga en cuenta que las rotaciones de las agujas del reloj se incluyen aquí, por ejemplo girando 270 ° a la derecha es igual al que gira 90 ° en sentido antihorario.
- reflexión a lo largo de la línea media vertical u horizontal, oa lo largo de los dos diagonales. Escribamos las reflexiones como ref V, ref H, ref D1 y D2 ref, respectivamente.
- Por último, el id operación idéntica dejando todo sin cambios es también una simetría.
Todos ellos mantienen la forma de la plaza sin cambios. (En las imágenes, los vértices son de color sólo para dejar en claro las operaciones).
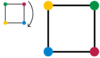 |  |  |  |  |  |  |
| Giro a la derecha por 90 ° 90 ° rot | Giro a la derecha por 180 ° rot 180 ° | Giro a la derecha por 270 ° rot 270 ° | Reflexión a lo largo de la ref vertical V | Reflexión a lo largo de la ref horizontal H | Reflexión lo largo de una diagonal ref D1 | Reflexión a lo largo de la otra diagonal ref D2 |
Este conjunto G de las simetrías es un ejemplo para un grupo, la llamada . grupo diedro de orden 8 Ser un grupo significa lo siguiente:
- Dos simetrías pueden estar compuestos, es decir, dados dos simetrías a y b, lo primero que puede ejecutar una y luego b y el resultado seguirá siendo una simetría. Escribimos el resultado b * a (que significa "b después de un"). Por ejemplo, girar por 270 ° y luego de rotación de 180 ° es igual a una rotación de 90 °, es decir, utilizando los símbolos anteriores, tenemos
- rot 180 ° * rot 270 ° = rot 90 °.
- En un lenguaje más formal, G está dotada de una operación binaria *, es decir, cualquiera de los dos elementos puede estar compuesta de un tercer elemento.
Aplicado a este grupo de ejemplo, la definición dice:
- Asociatividad : dado tres elementos a, b y c de G, (a * b) * c = a * (b * c).
- Elemento de identidad: No existe un elemento e en G tal que para todo a en G, e * a = a * e = a. En el ejemplo, el correo es sólo la simetría que deja todo sin cambios.
- Elemento inverso: Para cada una en G, existe un elemento b en G tal que a * b = b * a = e, donde e es un elemento de identidad. En el ejemplo, la rotación de un ángulo en sentido horario determinado y luego girando por el mismo ángulo en sentido antihorario saldrá de la plaza sin cambios y lo mismo es cierto si invertimos el orden, es decir, primero hacia la izquierda y luego hacia la derecha. Además, lo que refleja a lo largo de una diagonal, por ejemplo, se puede invertir mediante la aplicación de la misma reflexión de nuevo. En símbolos:
- Rot 270 ° * rot 90 ° = rot 90 ° * rot 270 ° = id y D1 ref * ref D1 = id.
Historia
Grupos de permutaciones ya estaban siendo estudiados en el siglo 18 y se aplicaron para resolver problemas en la teoría de ecuaciones. Sin embargo, la noción formal de un grupo no se publicó hasta finales del siglo 19 , y en ese momento los grupos había encontrado aplicaciones en la teoría de números , así como en la geometría .
Conceptos básicos de la teoría de grupos
Subgrupos
Un subconjunto H ⊂ G se llama subgrupo si la restricción de * a H es una operación de grupo en H. En otras palabras, es un grupo mediante la restricción de la operación definida en G. En el ejemplo anterior, las rotaciones constituyen un subgrupo, ya que una rotación compuesta con una rotación sigue siendo una rotación.
La prueba subgrupo es una condición necesaria y suficiente para un subconjunto H de un grupo G ser un subgrupo: es suficiente para comprobar que g -1 h ∈ H para todos g, h ∈ H. La cierre, bajo la operación de grupo y la inversión, de cualquier subconjunto no vacío de un grupo es un subgrupo.
Si G es un grupo finito, entonces también lo es H. Además, el orden de H divide el orden de G ( Teorema de Lagrange).
Los poderes de cualquier elemento de una y sus inversas (es decir, un 0 = e, a, a 2, a 3, a 4, ..., a -1, una -2, -3, un -4, ...) siempre formar un subgrupo del grupo más grande. Se dice que un genera ese subgrupo.
Un subgrupo H siempre define un conjunto de izquierda y derecha clases laterales. Teniendo en cuenta un elemento g arbitrario en G, la clase lateral izquierda de H que contiene g es
y la clase lateral derecha de H que contiene g es
Forma el conjunto de clases laterales izquierdas de H a partición de los elementos de G; es decir, dos clases laterales izquierdas o son iguales o tienen un vacío intersección . Lo mismo puede decirse de las clases laterales derechas de H. En general, las clases laterales izquierdos de H no son necesariamente iguales a las clases laterales derechas de H. Si es el caso que para todo g en G, gH = Hg, entonces H se dice que es una subgrupo normal.
Grupos cocientes
Si N es un subgrupo normal de G, su conjunto de clases laterales izquierdas y derechas clases laterales son iguales y uno puede hablar simplemente de la serie de clases laterales de N. En este caso, el conjunto de clases laterales de N puede estar equipado con una operación (a veces llamado multiplicación clase lateral, o adición clase lateral) para formar un nuevo grupo, llamado grupo cociente G / N. La operación entre las clases laterales se comporta de la mejor manera posible: (Ng) · (Nh) = N (gh) para todos los gyh en sol. Tenga en cuenta que el cociente N en sí sirve como la identidad de este grupo, y la inversa de Ng en el grupo cociente es (Ng) 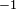 = N (g
= N (g 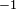 ).
).
Grupos simples
Si un grupo G no es el grupo trivial y sus únicos subgrupos normales son el grupo trivial y el propio grupo, se llama una grupo simple. Con la noción de grupos cocientes, que se puede expresar de forma equivalente como: Un grupo con sólo el grupo trivial y el grupo en sí como grupos cociente es simple.
Homomorfismos de grupo
Si G y H son dos grupos, A homomorfismo grupo f es un mapeo f: G → H que conserva la estructura de los grupos en cuestión. La estructura de los grupos están determinados por la operación del grupo, esto significa lo siguiente: si g y k son dos elementos en G, entonces
- f (GK) = f (g) f (k).
Este requisito garantiza que f (1 G) = 1 H, y también f (g) -1 = f (g -1) para todo g en G.
Dos grupos G y H son llamados isomorfos si existe un homomorfismo grupo f entre G y H que es a la vez sobreyectiva (a) y inyectiva (uno-a-uno).
La núcleo de un homomorfismo f se denota ker f y es el conjunto de elementos de G que se asignan a la identidad en H. Es decir, ker f = {g en G: f (g) = 1 H}. El núcleo de un homomorfismo es siempre un subgrupo normal. La Primero isomorfismo teorema establece que el imagen de un homomorfismo de grupos, f (G) es isomorfo al grupo cociente G / ker f. Un dato útil referente a homomorfismos es que son inyectivo si y sólo si su núcleo es trivial (es decir ker f = {1} G).
Grupos abelianos
Un grupo  se dice que es abeliano o conmutativo, si la operación cumple con la ley conmutativa. Es decir, para todos
se dice que es abeliano o conmutativo, si la operación cumple con la ley conmutativa. Es decir, para todos  y
y  en
en  ,
,  . Si no, el grupo se llama no abelian o no conmutativo. El nombre "abeliano" viene del matemático noruego Niels Abel. El ejemplo anterior de las simetrías de la plaza no es abeliano, porque
. Si no, el grupo se llama no abelian o no conmutativo. El nombre "abeliano" viene del matemático noruego Niels Abel. El ejemplo anterior de las simetrías de la plaza no es abeliano, porque
- pudrirse 90 ° * ref V = D2 ref ≠ ref D1 = ref V * rot 90 °
La centro de un grupo es un subgrupo que consiste de los elementos que se desplazan con cada otro elemento en el grupo. En un grupo conmutativo es el centro de todo el grupo; en el otro extremo hay grupos cuyo centro es trivial, es decir, que consiste únicamente en el elemento de identidad.
Los grupos cíclicos
Un grupo cíclico es un grupo cuyos elementos pueden estar generada por los sucesivos composición de la operación del grupo que se aplica a un solo elemento de dicho grupo. Un elemento con esta propiedad se llama un generador o un elemento primitivo del grupo. Los grupos cíclicos son abeliano.
Un grupo cíclico multiplicativo en la que G es el grupo, y a es un generador:
Un grupo cíclico aditivo, con un generador:
Si se aplica la composición sucesiva de la operación de la definición del grupo a un elemento no primitiva del grupo, una se genera subgrupo cíclico. De acuerdo a El teorema de Lagrange, el orden del subgrupo cíclico divide el orden del grupo. Por lo tanto, si el orden de un grupo finito es primordial , todos sus elementos, excepto el identidad, son elementos primitivos del grupo.
Orden de grupos y elementos
La orden de un grupo G, denotado generalmente por | G | u ocasionalmente por O (G), es el número de elementos en el conjunto G. Si la orden no es finito, entonces el grupo es un grupo infinito, denotado | G | = ∞.
El orden de un elemento a en un grupo G es el entero positivo n menos tal que una n = e, donde n representa una  , Es decir, la aplicación de la operación * a n copias de el valor a. (Si * representa la multiplicación, a continuación, un n corresponde a la enésima potencia de una). Si no hay tal n existe, entonces el orden de un se dice que es infinito. El orden de un elemento es el mismo que el orden del subgrupo cíclico generado por este elemento.
, Es decir, la aplicación de la operación * a n copias de el valor a. (Si * representa la multiplicación, a continuación, un n corresponde a la enésima potencia de una). Si no hay tal n existe, entonces el orden de un se dice que es infinito. El orden de un elemento es el mismo que el orden del subgrupo cíclico generado por este elemento.
El orden del grupo de muestra contiene ocho, el orden de la podredumbre de 90 ° es de cuatro, porque rotativo 4 veces por el 90 ° no está cambiando nada. El orden de los elementos de reflexión ref V etc. es de dos.
Las anotaciones y observaciones
Operación de Grupo
Los grupos pueden utilizar notación diferente dependiendo del contexto y de la operación del grupo.
- Grupos de aditivos utilizan + para denotar Además, y en el signo menos - para denotar inversas. Por ejemplo, a + (- a) = 0 en Z.
- Grupos multiplicativos utilizan *,
 , O el símbolo más general 'composición'
, O el símbolo más general 'composición'  para denotar la multiplicación, y el superíndice -1 para denotar inversas. Por ejemplo, a * a -1 = 1. Es muy común dejar caer el * y acaba de escribir aa -1 en lugar.
para denotar la multiplicación, y el superíndice -1 para denotar inversas. Por ejemplo, a * a -1 = 1. Es muy común dejar caer el * y acaba de escribir aa -1 en lugar. - Grupos de funciones utilizan • para denotar la composición de funciones, y el superíndice -1 a denotan inversas. Por ejemplo, g • g -1 = e. Es muy común dejar caer el • y acaba de escribir gg -1 en lugar.
La omisión de un símbolo para una operación es aceptable en general, y la deja al lector a conocer el contexto y la operación del grupo.
Al definir los grupos, es notación estándar para usar paréntesis en la definición del grupo y su funcionamiento. Por ejemplo, (H, +) denota el grupo formado por el conjunto H con la adición como operación de grupo. Para grupos como (Z n, +) y (F q *, *), el grupo multiplicativo de elementos no nulos en el campo finito F q, es común dejar caer los paréntesis y la operación (ya que sólo una operación hace que estos puesto en un grupo), como Z n y F q *. También es correcto referirse a un grupo por su identificador de conjunto, por ejemplo, H o  O para definir el grupo en notación set-constructor, siempre que quede claro qué grupo la operación que se pretende.
O para definir el grupo en notación set-constructor, siempre que quede claro qué grupo la operación que se pretende.
Elemento de identidad
Usando la propiedad de elemento de identidad, se puede demostrar que un grupo tiene exactamente un elemento de identidad. Por lo tanto uno generalmente habla de la identidad: suponen tanto eyf son elementos de identidad. Luego, porque f es una (derecha) identidad elemento e * f = e, y porque e es un (izquierda) identidad elemento e * f = f, de donde e = f.
El elemento de identidad e se conoce a veces como el "elemento neutro", y, a veces se denota por algún otro símbolo, dependiendo del grupo:
- En grupos multiplicativos, el elemento de identidad puede ser denotado por 1.
- En invertible grupos de la matriz, el elemento de identidad se indican con I o Id.
- En grupos de aditivos, el elemento de identidad puede ser denotado por 0.
- En grupos de funciones, el elemento de identidad por lo general se denota por f 0.
Si S es un subconjunto de G yx un elemento de G, entonces, en la notación multiplicativa, XS es el conjunto de todos los productos {xs: s en S}; Del mismo modo la notación Sx = {sx: s en S}; y durante dos subconjuntos S y T de G, escribimos ST para {st: s en S, t en T}. En notación aditiva, escribimos x + S, S + x, y T + S para los respectivos conjuntos (ver clases laterales).
Inverso
El inverso de un elemento A también puede ser demostrado ser único, y por lo general se escribe un -1 o - a, dependiendo del contexto. Supongamos dado un l inversa y otra inversa r. Entonces
- l = l * e = l * (a * r) = (L * a) * r = e * r = r.
Por otra parte, si en un grupo sólo sabemos que b * a = e, entonces esto es suficiente para concluir que b es el elemento inverso de una (ya que está garantizado un inverso de dos caras de una de existir, y entonces b debe ser igual IT). De manera similar a * b = e es suficiente para la misma conclusión.
(Sin embargo, un conjunto con una operación binaria puede tener muchos elementos de identidad izquierda o muchos elementos de identidad adecuadas, siempre que tenga nada de la clase opuesta: tomar, por ejemplo, en cualquier ajuste la operación definida por a * b = b, entonces cualquier elemento es un elemento de identidad izquierda, pero ninguno de ellos es un elemento de identidad derecho similar, en un monoide un elemento puede tener varios elementos inversos izquierda, siempre que no tiene elementos adecuados inversas (y viceversa):. el conjunto de todos los mapas a partir de un conjunto X infinita sí es un monoide bajo la composición de funciones, en el que cada mapa inyectiva tiene una inversa por la izquierda, y cada mapa surjective tiene una inversa derecha, pero ninguna de estas inversas es único en general. Sin embargo, si todos los elementos en un monoide tienen una inversa por la izquierda, la monoid puede demostrar ser un grupo).
Asociatividad
Para una secuencia de múltiples factores en un orden dado, se puede formar un producto de muchas maneras diferentes mediante la inserción de paréntesis; Sin embargo, por varias aplicaciones de la propiedad asociatividad, dos de ellos se puede demostrar que ser iguales. Por esta razón la expresión
- un 1 * 2 * ··· * a n
es ambigua y los paréntesis se omiten generalmente en este tipo de expresiones. Como consecuencia de ello casi nunca es necesario invocar explícitamente la propiedad asociatividad.
Las variantes de la definición
Algunas definiciones de un grupo usan condiciones aparentemente más débiles de identidad y elementos inversos. En lugar de requerir un elemento de identidad de dos lados, uno puede separado requieren la existencia de un elemento de identidad izquierda y derecha, y del mismo modo se puede requerir por separado la existencia de una serie de elementos inversos izquierdo y derecho: en ambos casos los elementos de izquierda y derecha pueden ser demostrado ser el mismo (y cada uno es único).
Ejemplos de grupos
Los enteros bajo la adición
El grupo probablemente más familiar es el conjunto de números enteros bajo adición . Uno puede pensar en los axiomas de un grupo que está siendo modelado en las propiedades de los números enteros Z = {..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...} , junto con la operación del grupo "+", que denota, como de costumbre, la adición. Los axiomas de comprobación son:
- Cierre: Si ayb son números enteros entonces a + b es un entero.
- Asociatividad: Si a, b, y c son números enteros, entonces (a + b) + c = a + (b + c).
- Elemento de identidad: 0 es un número entero y para cualquier número entero a, 0 + a = a + 0 = a.
- Elementos inversos: Si a es un número entero, entonces el número entero - a satisface las normas inversos: a + (- a) = (- a) + a = 0.
Este grupo también es abeliano porque a + b = b + a.
Si extendemos este ejemplo aún más teniendo en cuenta los números enteros con dos sumas y multiplicaciones, se forma una estructura algebraica más complicado llamado anillo. (Pero, tenga en cuenta que los números enteros con multiplicaciones no son un grupo.)
Algunos grupos multiplicativos
El término grupo multiplicativo se refiere a grupos cuyo funcionamiento se deriva de la multiplicación en un cierto sentido (dependiendo del contexto).
Los números enteros menores de multiplicación
Para empezar, le damos un contraejemplo: los números enteros con la operación de la multiplicación, denotado por "·". De acuerdo a la notación general, esto se denota (Z, ·). Satisface los axiomas de clausura, asociatividad y de identidad, pero no tiene en inversas: no es cierto que cada vez que a es un número entero, no es un número entero b tal que ab = ba = 1. Por ejemplo, a = 2 es un número entero, pero la única solución a la ecuación ab = 1 en este caso es b = 1/2. No podemos elegimos b = 1/2 1/2 porque no es un entero. Dado que no todos los elementos de (Z, ·) tiene una inversa (multiplicativo), (Z, ·) no es un grupo. Es, sin embargo, un conmutativa monoid, que es una estructura similar a un grupo, pero no requiere elementos inversos.
Los números racionales no nulos
La paso natural para remediar esta está considerando el conjunto de los números racionales Q, el conjunto de todas las fracciones de números enteros a / b, donde ayb son enteros y b es distinto de cero, y la operación de multiplicación, de nuevo denota por "·". Dado que el número racional 0 no tiene inverso multiplicativo, (Q, ·), como (Z, ·), no es un grupo.
Sin embargo, si en vez usamos el conjunto de todos los números racionales no nulo Q \ {0}, entonces (Q \ {0}, ·) no forman un grupo abeliano. De hecho, de cierre, de asociatividad y elemento de identidad axiomas son fáciles de comprobar y seguir de las propiedades de los números enteros (no perdamos de cierre mediante la eliminación de cero, ya que el producto de dos números racionales distintos de cero nunca es cero). Por último, la inversa de a / b es b / a, por lo tanto el axioma del elemento inverso es satisfecho.
Así como los números enteros forman una anillo, los números racionales forman la estructura algebraica de un campo, lo que permite las operaciones de suma, resta, multiplicación y división.
Grupos multiplicativos cíclicos
En (Q, ·), están los subgrupos cíclicos
- G = {a n, n ∈ Z} ⊂ Q
donde un n es el n -ésimo exponenciación del elemento primitivo de un grupo. Por ejemplo, si a es 2 entonces
Este grupo es un ejemplo de una grupo abeliano libre de rango uno: el rango es uno, porque G es generado por un elemento (una o equivalentemente un -1) y el grado de refino se refiere al hecho de que no se producen las relaciones entre los poderes de este generador. Por lo tanto, G, es isomorfo al grupo de números enteros (menores de adición) introdujo anteriormente.
Consindering el grupo
- {A n, n ∈ Z / Z} m,
el módulo m se une al grupo en un conjunto finito con un conjunto no fraccionada de elementos, ya la inversa (y  , Etc.) sería dentro del conjunto.
, Etc.) sería dentro del conjunto.
Los números enteros distintos de cero modulo un número primo
Las clases distintos de cero de números enteros modulo p, un número primo , forman un grupo bajo la multiplicación. El producto de dos números enteros ninguno de los cuales es divisible por p no es divisible por p, ya sea (porque p es primo), que muestra que el conjunto indicado de clases es cerrado bajo la multiplicación. La asociatividad es clara, y la clase de 1 es la identidad para la multiplicación, lo que queda por demostrar es que cada elemento tiene una inversa: dado un entero a no divisible por p, uno tiene que encontrar un número entero b tal que
 .
.
Esto se puede demostrar mediante el uso de la Algoritmo de Euclides, por ejemplo. En realidad, este ejemplo es similar a (Q \ {0}, ·) anterior, ya que resulta ser el grupo de elementos no nulos en la finito campo F p. Sin embargo, es claramente diferente del segundo grupo cíclico multiplicativo mencionado anteriormente.
Grupos finitos
Si el número de elementos de un grupo G es finito, entonces sí G se llama grupo finito. Skip grupo diedro del orden 8 es un ejemplo. Dos clases importantes son los siguientes:
- los grupos abelianos () cíclicos Z / n Z tratados anteriormente. Cualquier grupo abeliano finito es finito suma directa de grupos de este tipo, esto es parte de la teorema fundamental de los grupos abelianos finitamente generados.
- la grupo simétrico S N: es el grupo de permutaciones de letras N. Por ejemplo, el grupo simétrico en 3 letras S 3 es el grupo que consta de todas las posibles permutas de las tres letras ABC, es decir, contiene los elementos de ABC, ACB, ..., hasta CBA, en total 6 (o 3 factoriales ) elementos. Paralelamente al grupo de simetrías de la plaza anteriormente, S 3 también se puede interpretar como el grupo de simetrías de un triángulo equilátero.
El teorema de Cayley establece que cualquier grupo finito (no necesariamente abelian) se puede expresar como un subgrupo de una grupo simétrico S N.
La teoría de grupos Primaria
La teoría de grupos Primaria se ocupa de hechos básicos que tienen para todos los grupos individuales. Por ejemplo:
- Puede realizar la división en grupos; es decir, teniendo en cuenta los elementos A y B del grupo G, hay exactamente una solución de x en G a la ecuación x * a = b y exactamente una solución y en G a la ecuación y = a * b. De hecho, a la derecha, respectivamente, a la izquierda de multiplicación de la ecuación por un -1 da la solución x = b * a -1, respectivamente, y = a -1 * b.
- (calcetines y zapatos) El inverso de un producto es el producto de las inversas en el orden contrario: (a * b) -1 = b * a -1 -1.
- Prueba: Vamos a demostrar que (a * b) * (b * -1 a -1) = e, que como se mencionó anteriormente es suficiente para demostrar que -1 b * a -1 es la inversa de a * b.

= 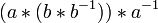
(Asociatividad) = 
(Definición de la inversa) = 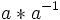
(Definición de elemento neutro) = 
(Definición de la inversa)
La construcción de nuevos grupos de otros dados
Además de los subgrupos y grupos cocientes son dos formas básicas de la construcción de nuevos grupos de otros dados. Otras técnicas de manipulación incluyen:
- Producto directo: Si (G, *) y (H, •) son grupos, entonces el conjunto G × H junto con la operación (1 g, h 1) (2 g, h 2) = (g 1 g * 2, h 1 h • 2) es un grupo. El producto directo también se puede definir con cualquier número de términos, finito o infinito, mediante el uso de la Producto cartesiano y la definición de la operación de coordenadas se refiere.
- Producto semidirecto: Si N y H son grupos y φ: H → Aut (N) es una homomorfismo de grupo, entonces el producto semidirecto de N y H con respecto a φ es el grupo (N × H, *), con * definida como
- (N 1, 1 h) * (n 2, 2 h) = (n 1 φ (h 1) (n 2), h 1 h 2)
- Suma externa directa: La suma externa directa de una familia de grupos es el subgrupo del producto constituido por elementos que tienen un número finito de coordenadas no identidad. Si la familia es finita la suma directa y el producto son equivalentes.
Las generalizaciones
| Estructuras de grupo como | |||||
| Totalidad * | Asociatividad | Identidad | Inversas | Conmutatividad | |
|---|---|---|---|---|---|
| Magma | Sí | No | No | No | No |
| Semigrupo | Sí | Sí | No | No | No |
| Monoid | Sí | Sí | Sí | No | No |
| Grupo | Sí | Sí | Sí | Sí | No |
| Grupo abeliano | Sí | Sí | Sí | Sí | Sí |
| Bucle | Sí | No | Sí | Sí | No |
| Cuasigrupo | Sí | No | No | Sí | No |
| Groupoid | No | Sí | Sí | Sí | No |
| Categoría | No | Sí | Sí | No | No |
| Semicategory | No | Sí | No | No | No |
| * El cierre, que se utiliza en muchas fuentes para definir estructuras de grupos similares, es un axioma equivalente a la totalidad, aunque se define de manera diferente. | |||||
En álgebra abstracta , las estructuras más generales surgen relajando algunos de los axiomas que definen un grupo.
- La eliminación del requisito de que cada elemento tiene una inversa, entonces la estructura algebraica resultante se denomina monoide.
- Un monoide sin identidad se denomina semigrupo.
- Alternativamente, se relaja el requisito de que la operación sea asociativo mientras que todavía requieren la posibilidad de división , la estructura algebraica resultante es una bucle.
- Un bucle sin identidad se llama cuasigrupo.
- Finalmente, cayendo todos los axiomas de la relación binaria, la estructura algebraica resultante se llama una magma.
Grupoides, que son similares a los grupos excepto que la composición a * b no necesita ser definida para todos los A y B, se plantea en el estudio de los tipos más complicados de simetrías, a menudo en estructuras topológicas y analítica. Grupoides, a su vez, son tipos especiales de categorías.
Supergrupos y Álgebras de Hopf son otras generalizaciones, y también lo son montones.
Grupos abelianos forman el prototipo para el concepto de categoría abeliana, que tiene aplicaciones en espacios vectoriales y más allá.
Leyes grupos formales son ciertas series formales que tienen propiedades muy similar a una operación de grupo.
En geometría diferencial , geometría algebraica y la topología , el concepto de grupo especializado para incluir grupos con una estructura adicional. Grupos de Lie, grupos algebraicos y grupos topológicos son ejemplos de agrupar objetos: estructuras de grupos como sentarse en una categoría distinta a la categoría ordinaria de conjuntos.