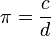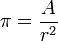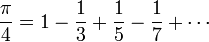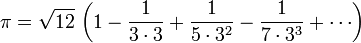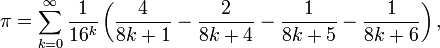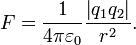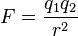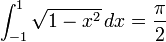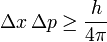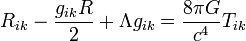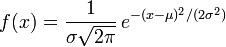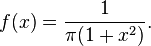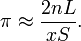Pi

Cuando el diámetro de un círculo es 1, su circunferencia es π.

Lista de los números - Números irracionales ζ (3) - √2 - √3 - √5 - φ - α - e - π - δ
Binario	11,00100100001111110110 ...
Decimal	3.14159265358979323846 ...
Hexadecimal	3.243F6A8885A308D31319 ...
Fracción continua	Tenga en cuenta que esta fracción continua no es periódica.

Pi o π es uno de los más importantes constantes matemáticas, aproximadamente igual a 3,14159. Representa la relación de cualquier círculo circunferencia 's a su diámetro en la geometría euclidiana , que es la misma que la relación del área de un círculo al cuadrado de su radio. Muchas fórmulas de matemáticas, ciencia y la ingeniería implican π.

Se trata de un número irracional , lo que significa que no puede ser expresado como una fracción m / n, donde m y n son números enteros . En consecuencia, su representación decimal nunca termina o las repeticiones. Más allá de ser irracional , es un número trascendental, lo que significa que ninguna secuencia finita de operaciones algebraicas en los números enteros (poderes, raíces, sumas, etc.) nunca podría producirlo. A lo largo de la historia de las matemáticas, se ha hecho mucho esfuerzo para determinar π más exactamente y entender su naturaleza; la fascinación con el número incluso ha transportado en cultura en general.

La letra griega π, a menudo enunciados pi en texto, fue adoptado para el número de la palabra griega para el perímetro "περίμετρος", probablemente por William Jones en 1706, y popularizado por Leonhard Euler algunos años más tarde. La constante es a veces también se conoce como la constante circular, Arquímedes 'constante (que no debe confundirse con una Arquímedes número), o Número de Ludolfo.

Fundamentos

La letra π

Π en minúscula (la letra minúscula se utiliza para la constante)

El nombre de la Letra griega π es pi, y este deletreo es de uso en contextos tipográficos cuando la letra griega no está disponible o cuando su uso podría ser problemático. Al referir a este constante, el símbolo π siempre se pronuncia como "pastel" en Inglés , la pronunciación Inglés convencional de la letra. En griego, el nombre de esta letra es pronunciada pi / /.

La constante se nombra "π" porque "π" es la primera letra de los griegos palabras περιφέρεια (periferia) y περίμετρος (perímetro), probablemente refiriéndose a su uso en la fórmula de encontrar la circunferencia, o el perímetro, de un círculo. π es Unicode carácter U + 03C0 (" pequeña letra griega pi ").

Definición

Circunferencia = π × diámetro

En la geometría plana euclidiana , π se define como la relación de un círculo 's circunferencia a su diámetro :

Tenga en cuenta que la relación ^c / _d no depende del tamaño del círculo. Por ejemplo, si un círculo tiene dos veces el diámetro d de otro círculo también tendrá el doble de la circunferencia c, la preservación de la relación ^c / _d. Este hecho es una consecuencia de la similitud de todos los círculos.

Área del círculo = π × área de la plaza a la sombra

Alternativamente π puede también ser definida como la relación de un círculo de área (A) para el área de un cuadrado cuyo lado es igual a la radio:

El π constante se puede definir de otras maneras que eviten los conceptos de longitud de arco y área, por ejemplo, como dos veces el más pequeño x positivo para que cos (x) = 0. Las fórmulas siguientes ilustran otras definiciones (equivalente).

La irracionalidad y la trascendencia

La constante π es un número irracional ; es decir, que no se puede escribir como la relación de dos números enteros . Esto fue demostrado en 1761 por Johann Heinrich Lambert. En el siglo 20, se han encontrado pruebas de que no requieren conocimiento previo más allá de cálculo integral. Uno de ellos, debido a Ivan Niven, es ampliamente conocida. Una prueba similar está un poco antes por María Cartwright.

Además, π es también trascendental, como quedó demostrado por Ferdinand von Lindemann en 1882 . Esto significa que no hay polinomio con racionales coeficientes de los cuales es un π raíz. Una consecuencia importante de la trascendencia de π es el hecho de que no es construible. Debido a que las coordenadas de todos los puntos que se pueden construir con compás y una regla son números construibles, es imposible la cuadratura del círculo: es decir, es imposible de construir, utilizando compás y una regla solo, un cuadrado cuya área es igual al área de un círculo dado.

Valor numérico

El valor numérico de π truncan a 50 cifras decimales es:

3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510

Ver los enlaces de abajo y los de secuencia A000796 en OEIS para más dígitos.

Mientras que el valor de pi se ha computado a más de un billones (10 ¹²⁾ dígitos, aplicaciones elementales, como el cálculo de la circunferencia de un círculo, que rara vez se requiere más de una docena de lugares decimales. Por ejemplo, un valor truncado de 39 cifras decimales es suficiente para calcular la circunferencia de cualquier círculo que se ajusta en el universo observable con una precisión comparable a la del tamaño de una átomo de hidrógeno.

π en sí tiene una infinita expansión decimal; porque π es un número irracional , su expansión decimal nunca termina y no repetir. Esta secuencia infinita de dígitos tiene fascinado a los matemáticos y laicos por igual, y mucho esfuerzo en los últimos siglos se ha puesto en computación más dígitos y la investigación de las propiedades de la numéricas. A pesar de tanto trabajo analítico, y cálculos del superordenador que han determinado más de 1 , nunca se ha encontrado un billón de dígitos de π sin un patrón sencillo en los dígitos. Los dígitos de π están disponibles en muchas páginas web, y hay software de cálculo de π a miles de millones de dígitos en cualquier ordenador personal .

Π Cálculo

π se puede medir empíricamente dibujando un círculo grande, entonces la medición de su diámetro y la circunferencia, desde la circunferencia de un círculo es siempre π veces su diámetro. Otro enfoque basado en la geometría, debido a Arquímedes , es dibujar un círculo imaginario de radio r centrado en el origen. El área del círculo se puede aproximar por inscribir un polígono regular dentro del círculo, y el cálculo del área del polígono; los más lados del polígono tiene, cuanto más cerca a la aproximación. Luego, utilizando la relación que el área A de un círculo es π veces el cuadrado del radio r, π se puede aproximar mediante el uso de:

π también puede calcularse utilizando métodos puramente matemáticos. La mayoría de las fórmulas utilizadas para calcular el valor de π tienen propiedades matemáticas deseables, pero son difíciles de entender sin un fondo en la trigonometría y cálculo . Sin embargo, algunos son bastante simples, como esta forma de la Serie Gregory-Leibniz:

.

Mientras que la serie es fácil de escribir y calcular, no es inmediatamente obvio por qué se produce π. Además, esta serie converge tan lentamente que 300 términos no son suficientes para calcular π correctamente a 2 cifras decimales.

Historia

La historia de π es paralela al desarrollo de las matemáticas en su conjunto. Algunos autores dividen los avances en tres períodos: el antiguo período durante el cual se estudió π geométricamente, la época clásica siguiendo el desarrollo del cálculo en Europa alrededor del siglo 17, y la edad de las computadoras digitales.

Período geométrico

Que la relación de la circunferencia al diámetro de un círculo es el mismo para todos los círculos, y que es ligeramente más de 3, era conocido por los antiguos geómetras egipcia, babilónica, indios y griegos. Las aproximaciones más antiguos conocidos datan de alrededor de 1900 aC; son 25/8 (Babilonia) y 256/81 (Egipto), tanto dentro del 1% del valor real. El texto indio Shatapatha Brahmana da π como 339/108 ≈ 3,139. La Tanaj parece sugerir, en el Libro de Reyes, que π = 3, que es notablemente peor que otras estimaciones disponibles en el momento de la escritura (600 aC). La interpretación del pasaje se discute, como algunos creen la relación de 3:. 1 es de una circunferencia exterior de un diámetro interior de una cuenca de paredes finas, que de hecho podría ser una relación precisa, en función del espesor de las paredes Ver: Valor bíblico del Pi.

Arquímedes (287-212 aC) fue el primero en calcular π rigurosamente. Se dio cuenta de que su magnitud puede estar delimitado desde abajo y por encima inscribiendo en círculos polígonos regulares y calcular respectivos perímetros de los polígonos exteriores e interiores ":

Al utilizar el equivalente de los polígonos de 96 lados, demostró que 223/71 <π <22/7. Tomando el promedio de estos valores se obtiene 3,1419. En los siglos siguientes, más importante desarrollo tuvo lugar en la India y China. Alrededor de 480, el matemático chino Zu Chongzhi dio la aproximación π = 355/113, y mostró que 3,1415926 <π <3,1415927, que se situaría como el valor más exacto de π en los próximos 900 años.

Período clásico

Hasta el segundo milenio, π era conocido por menos de 10 dígitos decimales. El siguiente avance importante en el estudio de π vino con el desarrollo de cálculo , y en particular el descubrimiento de serie infinita que en principio la posibilidad de calcular π a cualquier precisión deseada añadiendo suficientemente muchos términos. Alrededor de 1400, Madhava de Sangamagrama encontró la primera conocida como serie:

(Ahora conocido como el Serie Gregory-Leibniz desde que fue redescubierta por James Gregory y Gottfried Leibniz en el siglo 17). Desafortunadamente, la tasa de convergencia es demasiado lento para calcular el número de dígitos en la práctica; cerca de 4.000 términos deben ser sumados para mejorar la estimación de Arquímedes. Sin embargo, mediante la transformación de la serie en

Madhava fue capaz de calcular π como 3,14159265359, corregir a 11 cifras decimales. El récord fue batido en 1424 por el astrónomo persa Jamshid al-Kashi, quien determinó 16 decimales de π.

La primera contribución europea importante ya que Arquímedes fue hecha por el matemático alemán Ludolfo van Ceulen (1540-1610), que utilizó un método geométrico para calcular 35 decimales de π. Él estaba tan orgulloso del cálculo, que requiere la mayor parte de su vida, que tenía los dígitos grabados en su lápida.

Por la misma época, los métodos de cálculo y determinación de las series infinitas y productos para cantidades geométricas comenzaron a surgir en Europa. El primero de estos fue el representación La fórmula de Viète,

encontrado por François Viète en 1593. Otro resultado es famosa Producto de Wallis,

escrito por . John Wallis en 1655 Isaac Newton sí mismo deriva de una serie de π y calculados 15 dígitos, aunque más tarde confesó: "Me da vergüenza decirle a cuántas figuras llevé estos cálculos, que no tienen otro negocio en el momento."

John Machin fue el primero para calcular 100 decimales de π, utilizando la fórmula

con

Fórmulas de este tipo, ahora conocido como Machin fórmulas similares, se utilizan para establecer varios récords sucesivos y se mantuvo el método más conocido para el cálculo de π bien entrada la era de las computadoras. Un notable récord fue fijado por el prodigio de cálculo Zacarías Dase, que en 1844 empleó un Fórmulas de Machin para calcular 200 decimales de π en la cabeza. El mejor valor al final del siglo 19 se debió a William Shanks, que tomó 15 años para calcular π con 707 dígitos, aunque debido a un error sólo el primer 527 eran correctas. (Para evitar este tipo de errores, los cálculos de registro modernos de cualquier tipo a menudo se realizan dos veces, con dos fórmulas diferentes. Si los resultados son los mismos, es probable que sea correcta).

Los avances teóricos en el siglo 18 llevó a ideas sobre la naturaleza de π que no podría lograrse mediante cálculo numérico solo. Johann Heinrich Lambert demostró la irracionalidad de π en 1761, y Adrien-Marie Legendre demostró en 1794 que también π ² es irracional. Cuando Leonhard Euler en 1735 resolvió el famoso Problema de Basilea - encontrar el valor exacto de

que está π ^2/6, que establece una conexión profunda entre π y el números primos . Tanto Legendre y Leonhard Euler especularon que podría ser π trascendental, un hecho que fue demostrado en 1882 por Ferdinand von Lindemann.

William Jones libro Un Nuevo Introducción a la Matemática de 1706 se cita como el primer texto en el que el Letra griega π se utilizó para este constante, pero esta notación se hizo particularmente popular después de Leonhard Euler adoptó en 1737. Escribió:

Computación en la era de la informática

El advenimiento de las computadoras digitales en el siglo 20 dio lugar a un aumento de la tasa de nuevos registros de cálculo π. John von Neumann utiliza ENIAC para calcular 2.037 dígitos de π en 1949, un cálculo que tomó 70 horas. Miles adicionales de cifras decimales se obtuvieron en las décadas siguientes, con el hito del millón de dígitos aprobada en 1973. El progreso no se debió sólo a un hardware más rápido, pero también nuevos algoritmos. Uno de los desarrollos más significativos fue el descubrimiento de la transformada rápida de Fourier (FFT) en la década de 1960, que permite a los ordenadores para realizar operaciones aritméticas con números muy grandes rápidamente.

En el principio del siglo 20, el matemático indio Srinivasa Ramanujan encontró muchas fórmulas nuevas para π, algunos destacan por su elegancia y profundidad matemática. Una de sus fórmulas más famosas es la serie

que entrega 14 dígitos por plazo. Los hermanos Chudnovsky utilizado esta fórmula para establecer varios registros informáticos π en el final de la década de 1980, incluyendo el primer cálculo de más de mil millones (1011196691) decimales en 1989. Se mantiene la fórmula de elección para el cálculo de π software que se ejecuta en computadoras personales, en contraposición a la supercomputadoras se utilizan para configurar los registros modernos.

Mientras que la serie suelen aumentar la precisión con una cantidad fija por cada término agregado, existen algoritmos iterativos que multiplican el número de dígitos correctos en cada paso, con la desventaja de que cada paso requiere por lo general un cálculo costoso. Un gran avance se hizo en 1975, cuando Richard Brent y Eugene Salamin descubrió de forma independiente la Brent-Salamín algoritmo, que utiliza sólo la aritmética a duplicar el número de dígitos correctos en cada paso. El algoritmo consiste en establecer

y la iteración

hasta que un _n y b _n son lo suficientemente cerca. Entonces la estimación de π está dada por

.

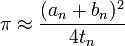Utilizando este esquema, 25 iteraciones son suficientes para llegar a 45 millones de decimales correctos. Un algoritmo similar que cuadruplica la exactitud en cada paso ha sido encontrado por Jonathan y Peter Borwein. Los métodos han sido utilizados por Yasumasa Kanada y equipo para establecer la mayor parte de los registros de cálculo π desde 1980, hasta un cálculo de decimales de π 206158430000 en 1999. El récord actual es de 1.241.100.000.000 decimales establecidos por Canadá y el equipo en el 2002. Aunque la mayor parte de los registros anteriores de Kanada se establecieron utilizando el algoritmo de Brent-Salamín, el cálculo 2002 hizo uso de dos fórmulas Machin-como que eran más lentos pero fundamentalmente reducen el consumo de memoria. El cálculo se realizó en un 64-nodo Hitachi superordenador con 1 terabyte de memoria principal, capaz de realizar 2,000,000,000,000 de operaciones por segundo.

Un importante acontecimiento reciente fue el Fórmula Bailey-Borwein-Plouffe (fórmula BBP), descubierto por Simon Plouffe y el nombre de los autores del artículo en el que la fórmula se publicó, David H. Bailey, Peter Borwein y Plouffe. La fórmula,

es notable, ya que permite la extracción de cualquier individuo hexadecimal o binario dígitos de π sin calcular todos los precedentes. Entre 1998 y 2000, la proyecto de computación distribuida PiHex utilizó una modificación de la fórmula BBP debido a Fabrice Bellard para calcular la cuadrillonésima (1.000.000.000.000.000: º) poco de π, que resultó ser 0.

Memorización de dígitos

Reciente décadas han visto un aumento en el número récord de dígitos memorizados.

Incluso mucho antes los ordenadores han calculado π, la memorización de un número récord de dígitos se convirtió en una obsesión para alguna gente. En el año 2006, Akira Haraguchi, ingeniero japonés jubilado, afirmó haber recitado 100.000 lugares decimales. Esto, sin embargo, aún no se ha verificado por Records Mundiales Guinness. El récord Guinness-reconocido para los dígitos recordados del π es 67.890 dígitos, en poder de Lu Chao, un estudiante de posgrado de 24 años de edad procedente de China. Le tomó 24 horas y 4 minutos para recitar a la posición decimal de π 67890a sin un error.

Hay muchas maneras para memorizar π, incluyendo el uso de "piems", que son poemas que representan π de una manera tal que la longitud de cada palabra (en letras) representa un dígito. He aquí un ejemplo de un piem: ¿Cómo yo necesito una bebida, alcohólica en la naturaleza (o: por supuesto)., Después de las conferencias pesadas que implican la mecánica cuántica Observe cómo la primera palabra tiene 3 letras, la segunda palabra tiene 1, el tercero tiene 4, el cuarto tiene 1, el quinto tiene 5, y así sucesivamente. La Cadaeic Cadenza contiene los primeros 3834 dígitos de π de esta manera. Piems están relacionados con todo el campo de estudio de humor con todo serio que implica el uso de técnicas mnemotécnicas para recordar los dígitos de π, conocidos como piphilology. Ver Mnemotécnicos Pi para ejemplos. En otros idiomas hay métodos similares de memorización. Sin embargo, este método resulta ineficiente para grandes memorizaciones de pi. Otros métodos incluyen patrones de recordación en los números; por ejemplo, el año 1971 aparece en los primeros cincuenta dígitos de pi.

Propiedades avanzadas

Aproximaciones numéricas

Debido a la naturaleza trascendental de π, no hay expresiones de forma cerrada para el número en términos de números y funciones algebraicas. Las fórmulas para calcular π usando aritmética elemental suele incluir serie o notación de sumatoria (tales como "..."), lo que indica que la fórmula es realmente una fórmula para una secuencia infinita de aproximaciones a π. Cuantos más términos incluidos en un cálculo, el más cercano a π el resultado obtendrá.

En consecuencia, los cálculos numéricos deben utilizar aproximaciones de π. Para muchos propósitos, 3,14 o _^22/7 es lo suficientemente cerca, aunque los ingenieros a menudo usan 3.1416 (5 cifras significativas) o 3,14159 (6 cifras significativas) para mayor precisión. Las aproximaciones _^22/7 y _^355/113, con 3 y 7 cifras significativas, respectivamente, se obtienen a partir de la simple continua expansión fracción de π. La aproximación _^355/113 (3,1415929 ...) es la mejor que se puede expresar con una de tres dígitos o cuatro dígitos numerador y el denominador .

La aproximación numérica primera de π es casi seguro que el valor 3. En los casos donde se requiere poca precisión, puede ser un sustituto aceptable. Esa 3 es una subestimación se deduce del hecho de que es la relación de la perímetro de una inscrita regular de hexágono a la de diámetro de la círculo .

Naturalidad

En la geometría no euclidiana la suma de los ángulos de un triángulo puede ser más o menos de π radianes , y la relación de la circunferencia de un círculo y su diámetro también puede diferir de π. Esto no cambia la definición de π, pero sí afecta a muchas fórmulas en las que π aparece. Así, en particular, π no se ve afectado por la forma del universo; no es una constante física, sino una constante matemática definida con independencia de las medidas físicas. Sin embargo, ocurre a menudo en la física.

Por ejemplo, considere la ley de Coulomb ( Unidades del SI):

Aquí, 4 πr ² es sólo el área de la superficie de la esfera de radio r. De esta forma, es una manera conveniente de describir la relación inversa del cuadrado de la fuerza a una distancia r de una fuente puntual. Sería, por supuesto, ser posible describir esta ley en otra, pero menos conveniente maneras, o en algunos casos más conveniente. Si Carga de Planck se utiliza, puede ser escrito como

y así eliminar la necesidad de π.

Preguntas abiertas

La pregunta abierta más apremiante sobre π es si se trata de un número normal - si algún bloque de dígitos se produce en la expansión de π con la misma frecuencia, como es de esperar estadísticamente si los dígitos se habían producido completamente "al azar", y que esto es cierto en todas las bases, no sólo basar 10. El conocimiento actual sobre este punto es muy débil; por ejemplo, ni siquiera se sabe cuál de los dígitos 0, ..., 9 ocurren infinitas veces en la expansión decimal de π.

Bailey y Crandall mostraron en 2000 que la existencia de la anteriormente mencionada Fórmula Bailey-Borwein-Plouffe y fórmulas similares implican que la normalidad en base 2 de π y varias otras constantes se puede reducir a un plausibles conjeturas de la teoría del caos .

También se desconoce si π y e son algebraicamente independiente, aunque Yuri Nesterenko demostró la independencia algebraica de {π, e ^π, Γ (1/4)} en 1996. Sin embargo, se sabe que al menos uno de πe y π + e es trascendental (ver Lindemann-Weierstrass).

Utilice en matemáticas y ciencias

π es ubicuo en las matemáticas, apareciendo incluso en lugares que carecen de una conexión obvia a los círculos de la geometría euclidiana.

Geometría y trigonometría

Para cualquier círculo con radio r y el diámetro d = 2 r, la circunferencia es π d y la zona es π r ^2. Además, π aparece en fórmulas de áreas y volúmenes de muchas otras formas geométricas basadas en círculos, como elipses , esferas , conos y toros . En consecuencia, π aparece en integrales definidas que describen circunferencia, área o volumen de formas generadas por los círculos. En el caso básico, la mitad del área de la disco unidad está dada por:

y

da la mitad de la circunferencia de la círculo unidad. Formas más complicadas se pueden integrar como sólidos de revolución.

A partir de la definición de unidad-círculo de las funciones trigonométricas también se desprende que el seno y el coseno tienen período 2π. Es decir, para todos los x y n números enteros, sin (x) = sin (x + 2π n) y cos (x) = cos (x + 2π n). Porque el pecado (0) = 0, sin (2π n) = 0 para todos los enteros n. Además, la medida del ángulo de 180 ° es igual a π radianes. En otras palabras, 1 ° = (π / 180 radianes).

En la matemática moderna, π se define a menudo el uso de funciones trigonométricas, por ejemplo, como las x positivas más pequeños para que sen x = 0, para evitar la dependencia innecesaria en las sutilezas de la geometría euclidiana y la integración. De manera equivalente, π se puede definir mediante el funciones trigonométricas inversas, por ejemplo como π = 2 arccos (0) o π = 4 arctan (1). Ampliando las funciones trigonométricas inversas como serie de potencias es la forma más fácil de obtener series infinitas para π.

Análisis Superior y la teoría de números

La frecuente aparición de π en análisis complejo puede estar relacionado con el comportamiento de la función exponencial de una variable compleja, descrita por La fórmula de Euler

donde i es la unidad imaginaria satisfacer i ² = -1 y e ≈ 2,71828 es Número de Euler. Esta fórmula supone que las potencias imaginarias de e describen rotaciones en el círculo unidad en el plano complejo; estas rotaciones tienen un período de 360 ° = 2π. En particular, los 180 ° de rotación φ = π resultados en la notable identidad de Euler

Hay n diferente n -ésimo raíces de la unidad

La Integral de Gauss

Una consecuencia es que la función gamma de un medio entero es un múltiplo racional de √π.

Física

El π número aparece habitualmente en las ecuaciones que describen los principios fundamentales del Universo, debido en gran parte a su relación con la naturaleza del círculo y, correspondientemente sistemas, coordinar esférica.

• La constante cosmológica:

• Principio de incertidumbre de Heisenberg:

• Ecuación de campo de Einstein de la relatividad general :

• La ley de Coulomb para la fuerza eléctrica :

• La permeabilidad magnética del espacio libre:

• Tercera constante de la ley de Kepler :

Probabilidad y estadística

En probabilidad y estadística , hay muchas distribuciones cuyas fórmulas contienen π, incluyendo:

• la función de densidad de probabilidad para la distribución normal con media μ y desviación estándar σ, debido a la Integral de Gauss:

• la función de densidad de probabilidad para la (estándar) Distribución de Cauchy:

Tenga en cuenta que ya 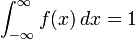para cualquier función de densidad de probabilidad f (x), las fórmulas anteriores pueden ser usados para producir otras fórmulas integrales para π.

Problema de la aguja de Buffon a veces se cita como una aproximación empírica de π en "matemáticas populares" funciona. Considere la posibilidad de dejar caer una aguja de longitud L repetidamente sobre una superficie que contiene líneas paralelas dibujadas unidades S aparte (con S> L). Si la aguja se deja caer n veces y x de esas veces se trata de descansar cruzar una línea (x> 0), entonces uno puede aproximar π usando el método de Monte Carlo :

Aunque este resultado es matemáticamente impecable, no se puede utilizar para determinar más de muy pocos dígitos de π por experimento. Conseguir de forma fiable sólo tres dígitos (incluyendo el inicial "3") derecho requiere millones de lanzamientos, y el número de lanzamientos crece exponencialmente con el número de dígitos deseados. Además, cualquier error en la medición de las longitudes L y S transferirá directamente a un error en el π aproximada. Por ejemplo, una diferencia de un solo átomo en la longitud de una aguja de 10 centímetros se mostraría en torno a la novena dígitos del resultado. En la práctica, las incertidumbres en la determinación de si la aguja en realidad cruza una línea cuando parece tocar exactamente que limitará la precisión alcanzable a mucho menos de 9 dígitos.