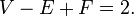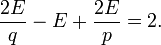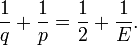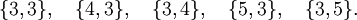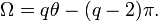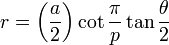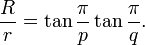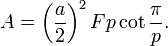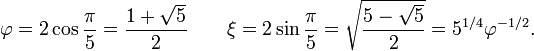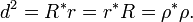Sólidos platónicos

Temas relacionados: Matemáticas

Sabías ...

Esta selección Escuelas fue originalmente elegido por SOS para las escuelas en el mundo en desarrollo que no tienen acceso a Internet. Está disponible como una descarga intranet. Haga clic aquí para obtener información sobre el apadrinamiento de niños.

'Sólido platónico' es un convexo poliedro regular. Estos son los análogos tridimensionales de la convexo polígonos regulares. No son precisamente cinco figuras (que se muestran a continuación). Ellos son los únicos que las caras, aristas y ángulos son todos congruentes.

El Cinco poliedros regulares convexos (sólidos platónicos)
Tetraedro	Hexahedron o Cube	Octaedro	Dodecaedro	Icosaedro
( Animación )	( Animación )	( Animación )	( Animación)	( Animación )

El nombre de cada figura se deriva del número de sus caras, respectivamente: 4, 6, 8, 12, y 20.

La belleza estética y la simetría de los sólidos platónicos han hecho un tema favorito de geómetras durante miles de años. Se nombran para el filósofo griego Platón teorizó que la elementos clásicos se construyen a partir de los sólidos regulares.

Historia

Modelo sólido platónico de Kepler del sistema solar desde Cosmographicum Mysterium (1596)

Los sólidos platónicos son conocidos desde la antigüedad. Modelos adornados de ellos se pueden encontrar entre la bolas de piedra talladas creados por la tarde pueblo neolítico de Escocia al menos 1000 años antes de Platón (Atiyah y Sutcliffe 2003).

Los antiguos griegos estudiaron los sólidos platónicos ampliamente. Algunas fuentes (tales como Proclo) crédito Pitágoras con su descubrimiento. Otra evidencia sugiere que puede haber sido sólo familiarizado con el tetraedro, cubo y el dodecaedro, y que el descubrimiento del octaedro y el icosaedro pertenecen a Teeteto, un contemporáneo de Platón. En cualquier caso, Teeteto dio una descripción matemática de los cinco y pudo haber sido el responsable de la primera prueba conocida de que no hay otros poliedros regulares convexos.

Los sólidos platónicos ocupan un lugar destacado en la filosofía de Platón para quien que se nombran. Platón escribió sobre ellos en el diálogo Timeo c 0.360 aC en la que asocia cada uno de los cuatro elementos clásicos ( tierra, aire, agua, y fuego) con un sólido regular. Tierra se asoció con el cubo, el aire con el octaedro, el agua con el icosaedro, y dispara con el tetraedro. No había justificación intuitiva para estas asociaciones: el calor del fuego se siente agudo y punzante (como poco tetraedros). El aire está compuesto del octaedro; sus componentes minúsculos son tan suaves que uno apenas puede sentirlo. El agua, el icosaedro, fluye de la mano de uno al recogerlo, como si estuviera hecha de pequeñas bolitas. Por el contrario, un sólido altamente no-esférica, el hexaedro (cubo) representa la tierra. Estos pequeños sólidos torpes causan suciedad a resquebrajarse y romperse al recogerlo, en clara diferencia con la fluidez del agua. El quinto sólido platónico, el dodecaedro, Platón comentarios oscuramente, "... el dios usado para disponer las constelaciones en el cielo entero". Aristóteles añadió un quinto elemento, aither (éter en latín, "éter" en Inglés) y postularon que los cielos fueron hechos de este elemento, pero no tenía ningún interés en juego con Platón quinto sólido.

Euclides dio una descripción matemática completa de los sólidos platónicos en los Elementos ; el último libro (libro XIII) de los cuales está dedicado a sus propiedades. Proposiciones 13 a 17 en el Libro XIII describen la construcción del tetraedro, octaedro, cubo, icosaedro y dodecaedro en ese orden. Para cada sólido Euclides encuentra la relación entre el diámetro de la esfera circunscrita a la longitud del borde. En la Proposición 18, argumenta que no hay poliedros regulares convexos más. Mucha de la información en el libro XIII se deriva probablemente de la obra de Teeteto.

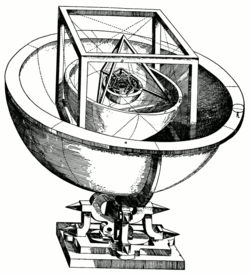
En el siglo 16 , la Alemán el astrónomo Johannes Kepler intentó encontrar una relación entre los cinco conocidos planetas en ese momento (excluyendo la Tierra) y los cinco sólidos platónicos. En Mysterium Cosmographicum, publicado en 1596, Kepler estableció un modelo del sistema solar en el que los cinco sólidos se establecen dentro de otro y separados por una serie de esferas inscritos y circunscritos. Las seis esferas correspondían a cada uno de los planetas ( Mercurio , Venus , Tierra , Marte , Júpiter y Saturno ). Los sólidos se ordenan con la más interna es el octaedro, seguido por el icosaedro, dodecaedro, tetraedro, y finalmente el cubo. De esta manera la estructura del sistema solar y las relaciones de distancia entre los planetas fue dictada por los sólidos platónicos. Al final, la idea original de Kepler tuvo que ser abandonado, pero fuera de su investigación fue el descubrimiento de la Sólidos de Kepler, la constatación de que las órbitas de los planetas no son círculos, y las leyes de Kepler del movimiento planetario de la que es ahora famoso.

Propiedades combinatorias

Un poliedro convexo es un sólido platónico si y sólo si

todas sus caras son convexa congruentes polígonos regulares,
ninguno de sus caras se cruzan, excepto en sus bordes, y
el mismo número de caras se reúnen en cada uno de sus vértices.

Por tanto, cada lata sólido platónico se denota por el símbolo {p, q} donde

p = el número de lados de cada cara (o el número de vértices de cada cara) y

q = el número de caras que se encuentran en cada vértice (o el número de aristas reunión en cada vértice).

El símbolo {p, q}, llamado Símbolo de Schläfli, da una combinatoria descripción del poliedro. Los símbolos de Schläfli de los cinco sólidos platónicos se dan en la siguiente tabla.

Poliedro	Vértices	Bordes	Caras	Símbolo de Schläfli	Vértice configuración
tetraedro	4	6	4	{3, 3}	3.3.3
cubo	8	12	6	{4,} 3	4.4.4
octaedro	6	12	8	{3, 4}	3.3.3.3
dodecaedro	20	30	12	{5, 3}	5.5.5
icosaedro	12	30	20	{3, 5}	3.3.3.3.3

Toda otra información combinatoria de estos sólidos, como el número total de vértices (V), los bordes (E), y caras (F), se puede determinar a partir de p y q. Desde cualquier borde une dos vértices y tiene dos caras adyacentes debemos tener:

$pF = 2E = qV. \,$

El otro tipo de relación entre estos valores está dada por la fórmula de Euler :

$V - E + F = 2. \,$

Este hecho no trivial puede ser probado en una gran variedad de formas (en topología algebraica se deduce del hecho de que la característica de Euler de la esfera es 2). En conjunto, estas tres relaciones determinan completamente V, E, y F:

$V = \ frac {4p} {4 - (p-2) (q-2)}, \ quad E = \ frac {2pq} {4 - (p-2) (q-2)}, \ quad F = \ frac {4q} {4 - (p-2) (q-2)}.$

Tenga en cuenta que intercambiar pyq intercambios F y V, dejando sin cambios E (Para una interpretación geométrica de este hecho ver la sección sobre la doble poliedros abajo).

Clasificación

Es un resultado clásico que sólo hay cinco poliedros regulares convexos. Dos argumentos comunes se dan a continuación. Ambos de estos argumentos sólo demuestran que no puede haber más de cinco sólidos platónicos. Que los cinco realidad existen es una pregunta de uno independiente que puede ser respondida por una construcción explícita.

Prueba geométrica

El siguiente argumento geométrica es muy similar a la dada por Euclides en los Elementos:

Cada vértice del sólido debe coincidir con un vértice de cada uno de al menos tres caras.
En cada vértice del sólido, el total, entre las caras adyacentes, de los ángulos entre sus respectivos lados adyacentes debe ser inferior a 360 °.
Los ángulos en los vértices de todas las caras de un sólido platónico son idénticas, por lo que cada vértice de cada cara deben contribuir menos de 360 ° / 3 = 120 °.
Polígonos regulares de seis o más partes tienen solamente ángulos de 120 ° o más, por lo que la cara común debe ser el triángulo, cuadrado o pentágono. Y para:
- Triangular caras: cada vértice de un triángulo equilátero es de 60 °, por lo que una forma puede tener 3, 4, o 5 triángulos reunidos en un vértice; estos son el tetraedro, el octaedro y el icosaedro, respectivamente.
- Plaza caras: cada vértice de un cuadrado es 90 °, por lo que sólo hay una posible disposición con tres caras en un vértice, el cubo.
- Pentagonal enfrenta: cada vértice es de 108 °; de nuevo, sólo una disposición, de tres caras en un vértice es posible, el dodecaedro.

Prueba topológica

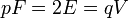Un puramente topológica prueba se puede hacer usando sólo información combinatoria sobre los sólidos. La clave es la observación de Euler que $V - E + F = 2$ , Y el hecho de que $pF = 2E = qV$ . Combinando estas ecuaciones se obtiene la ecuación

$\ Frac {2E} {q} - E + \ frac {2E} {p} = 2.$

Manipulación algebraica simple entonces da

${1 \ over q} + {1 \ over p} = {1 \ over 2} + {1 \ sobre E}.$

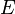Desde $E$ es estrictamente positivo debemos tener

$\ Frac {1} {q} + \ frac {1} {p}> \ frac {1} {2}.$

Usando el hecho de que p y q deben ser ambos al menos 3, uno puede ver fácilmente que sólo hay cinco posibilidades de {p, q}:

$\ {3, 3 \}, \ quad \ {4, 3 \}, \ quad \ {3, 4 \}, \ quad \ {5, 3 \}, \ quad \ {3,5 \}.$

Propiedades geométricas

Angles

Hay un número de ángulos asociados con cada sólido platónico. La ángulo diedro es el ángulo interior entre los dos planos de la cara. El ángulo diedro, θ, del sólido {p, q} está dada por la fórmula

$\ Sin {\ theta \ over 2} = \ frac {\ cos (\ pi / q)} {\ sin (\ pi / p)}.$

Esto es a veces más convenientemente expresada en términos de la tangente por

$\ Bronceado {\ theta \ over 2} = \ frac {\ cos (\ pi / q)} {\ sin (\ pi / h)}.$

La cantidad h es de 4, 6, 6, 10, y 10 para el tetraedro, cubo, octaedro, dodecaedro, icosaedro y respectivamente.

La deficiencia angular en el vértice de un poliedro es la diferencia entre la suma de los ángulos de la cara en ese vértice y 2π. El defecto, δ, en cualquier vértice de los sólidos platónicos {p, q} es

$\ Delta = 2 \ pi - q \ pi \ left (1- {2 \ over p} \ right).$

Por Teorema de Descartes, esto es igual a 4π dividido por el número de vértices (es decir, el defecto completo en todos los vértices es 4π).

El análogo de 3-dimensional de un ángulo plano es una ángulo sólido. El ángulo sólido, Ω, en el vértice de un sólido platónico se da en términos del ángulo diedro de

$\ Omega = q \ theta -. (Q-2) \ pi \,$

Así se desprende del exceso de fórmula esférica para una polígono esférico y el hecho de que la figura de la cima del poliedro {p, q} es un q regulares gon.

Los diversos ángulos asociados con los sólidos platónicos se tabulan a continuación. Los valores numéricos de los ángulos sólidos se dan en estereorradianes. La constante φ = (1 + √5) / 2 es el número áureo .

Poliedro	Ángulo diedro $(\ Theta) \,$	$\ Tan \ frac {\ theta} {2}$	Defecto $(\ Delta) \,$	Ángulo sólido 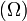$(\ Omega) \,$
tetraedro	70.53 °	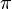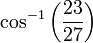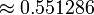$1 \ over {\ sqrt 2}$	$\ Pi \,$	$\ Cos ^ {- 1} \ left (\ frac {23} {27} \ right)$	$\ Aprox 0.551286$
cubo	90 °	$1 \,$	$\ Pi \ over 2$	$\ Frac {\ pi} {2}$	$\ Aprox 1.57080$
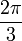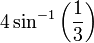octaedro	109.47 °	$\ Sqrt 2$	${2 \ pi} \ over 3$	$4 \ sin ^ {- 1} \ left ({1 \ over 3} \ right)$	$\ Aprox 1.35935$
dodecaedro	116.57 °	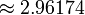$\ Phi \,$	$\ Pi \ over 5$	$\ Pi - \ tan ^ {- 1} \ left (\ frac {2} {11} \ right)$	$\ Aprox 2.96174$
icosaedro	138.19 °	$\ Phi ^ 2 \,$	$\ Pi \ over 3$	$2 \ pi - 5 \ sin ^ {- 1} \ left ({2 \ over 3} \ right)$	$\ Aprox 2.63455$

Radios, área y volumen

Otra de las virtudes de la regularidad es que los sólidos platónicos todos poseen tres esferas concéntricas:

la esfera circunscrita que pasa a través de todos los vértices,
la midsphere que es tangente a cada borde en el punto medio del borde, y
la esfera inscrita que es tangente a cada cara en el centro de la cara.

La radios de estas esferas se llaman la circunferencia circunscrita, la midradius, y el inradio. Estas son las distancias desde el centro del poliedro a los vértices, puntos medios del borde, y los centros de la cara, respectivamente. El R circunradio y la inradio r del sólido {p, q} de arista una se dan por

$R = \ left ({a \ over 2} \ right) \ tan \ frac {\ pi} {q} \ tan \ frac {\ theta} {2}$

$r = \ left ({a \ over 2} \ right) \ cot \ frac {\ pi} {p} \ tan \ frac {\ theta} {2}$

donde θ es el ángulo diedro. El ρ midradius está dada por

$\ Rho = \ left ({a \ over 2} \ right) \ frac {\ cos (\ pi / p)} {\ sin (\ pi / h)}$

donde h es la cantidad utilizada anteriormente en la definición del ángulo diedro (h = 4, 6, 6, 10, o 10). Tenga en cuenta que la relación de la circunferencia circunscrita a la inradio es simétrica en p y q:

${R \ over r} = \ tan \ frac {\ pi} {p} \ tan \ frac {\ pi} {q}.$

La área superficial, A, de un sólido platónico {p, q} se calcula fácilmente como área de un regulares veces p -gon el número de caras F. Esto es:

$A = \ left ({a \ over 2} \ right) ^ 2 Fp \ cot \ frac {\ pi} {p}.$

El volumen se calcula como F veces el volumen de la pirámide cuya base es un p gon regular y cuya altura es la inradio r. Esto es,

$V = {1 \ over 3} rA.$

La siguiente tabla muestra los distintos radios de los sólidos platónicos junto con su área de superficie y volumen. El tamaño total se fija mediante la adopción de la longitud del borde, a, que es igual a 2.

Poliedro (A = 2)	Inradio (r)	Midradius (ρ)	Circunradio (R)	Superficie (A)	Volumen (V)
tetraedro	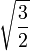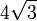$1 \ over {\ sqrt 6}$	$1 \ over {\ sqrt 2}$	$\ Sqrt {3 \ over 2}$	$4 \ sqrt 3$	$\ Frac {2 \ sqrt 2} {3}$
cubo	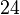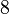$1 \,$	$\ Sqrt 2$	$\ Sqrt 3$	$24 \,$	$8 \,$
octaedro	$\ Sqrt {2 \ over 3}$	$1 \,$	$\ Sqrt 2$	$8 \ sqrt 3$	$\ Frac {8 \ sqrt 2} {3}$
dodecaedro	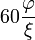$\ Frac {\ phi ^ 2} {\ xi}$	$\ Phi ^ 2$	$\ Sqrt 3 \, \ varphi$	$60 \ frac {\ phi} {\ xi}$	$20 \ frac {\ varphi ^ 3} {\ xi ^ 2}$
icosaedro	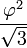$\ Frac {\ phi ^ 2} {\ sqrt 3}$	$\ Varphi$	$\ Xi \ varphi$	$20 \ sqrt 3$	$\ Frac {20 \ phi ^ 2} {3}$

Las constantes y φ ξ en lo anterior se dan por

$\ Phi = 2 \ cos {\ pi \ over 5} = \ frac {1+ \ sqrt 5} {2} \ qquad \ xi = 2 \ sin {\ pi \ over 5} = \ sqrt {\ frac {5- \ sqrt 5} {2}} = 5 ^ {1/4} \ phi ^ {- 1/2}.$

Entre los sólidos platónicos, ya sea el dodecaedro o icosaedro pueden verse como la mejor aproximación a la esfera. El icosaedro tiene el mayor número de caras, el ángulo diedro más grande, y se abraza a su esfera inscrita el más apretado. El dodecaedro, por otro lado, tiene el defecto angular más pequeño, el ángulo sólido más grande de vértice, y se llena a cabo su esfera circunscrita más.

Simetría

Poliedros Dual

Un cubo-octaedro dual.

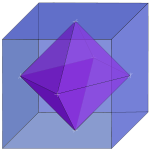
Cada poliedro tiene una poliedro dual con caras y vértices intercambiados. El dual de cada sólido platónico es otro sólido platónico, por lo que podemos organizar los cinco sólidos en pares duales.

El tetraedro es auto-dual (es decir, su doble es otro tetraedro).
El cubo y el octaedro forman un par dual.
El dodecaedro y el icosaedro forman un par dual.

Si un poliedro tiene Schläfli símbolo {p, q}, y después de su doble tiene el símbolo {q, p}. De hecho cada propiedad combinatoria de un sólido platónico puede ser interpretado como otra propiedad combinatoria de la doble.

Se puede construir el poliedro dual mediante la adopción de los vértices de la doble ser los centros de las caras de la figura original. Los bordes de la dual se forman mediante la conexión de los centros de las caras adyacentes en el original. De esta manera, el número de caras y vértices se intercambia, mientras que el número de bordes sigue siendo el mismo.

Más generalmente, se puede dualizar un sólido platónico con respecto a una esfera de radio d concéntrico con el sólido. Los radios (R, ρ, r) de un sólido y los de su doble (R *, ρ *, R *) están relacionados por

$d ^ 2 = R ^ \ ast r = r ^ \ ast R = \ rho ^ \ ast \ rho.$

A menudo es conveniente para dualizar con respecto a la midsphere (d = ρ), ya que tiene la misma relación con ambos poliedros. Tomando d ² = Rr da una doble sólido con la misma circunradio y inradio (es decir, R * = R y R * = r).

Grupos de simetría

En matemáticas, el concepto de simetría se estudia con la idea de un grupo de matemática . Cada poliedro ha asociado una grupo de simetría, que es el conjunto de todas las transformaciones ( Isometrías euclidianas) que dejan el invariante poliedro. La orden del grupo de simetría es el número de simetrías del poliedro. A menudo se distingue entre el grupo de simetría completa, que incluye reflexiones, y el grupo de simetría adecuada, que incluye sólo rotaciones.

Los grupos de simetría de los sólidos platónicos son conocidos como grupos poliédricos (que son una clase especial de la grupos de puntos en tres dimensiones). El alto grado de simetría de los sólidos platónicos se puede interpretar en un número de maneras. Lo más importante, los vértices de cada sólido son todos equivalentes en virtud de la acción del grupo de simetría, como son los bordes y caras. Se dice la acción del grupo de simetría es transitiva en los vértices, aristas y caras. De hecho, esta es otra manera de definir la regularidad de un poliedro: un poliedro es regular si y sólo si es vértice uniforme, borde uniforme, y cara uniforme.

Sólo hay tres grupos de simetría asociados con los sólidos platónicos en lugar de cinco, ya que el grupo de simetría de cualquier poliedro coincide con el de su doble. Esto se ve fácilmente mediante el examen de la construcción de la doble poliedro. Cualquier simetría del original debe ser una simetría de la doble y viceversa. Los tres grupos poliédricos son:

la grupo tetraédrico T,
la octaédrica grupo O (que es también el grupo de simetría del cubo), y
la icosaédrica grupo I (que es también el grupo de simetría del dodecaedro).

Las órdenes de los grupos (rotación) adecuados son 12, 24 y 60, respectivamente -, precisamente, el doble del número de aristas en los respectivos poliedros. Las órdenes de los grupos de simetría completos son el doble de lo nuevo (24, 48 y 120). Ver (Coxeter 1973) para una derivación de estos hechos.

La siguiente tabla muestra las diferentes propiedades de simetría de los sólidos platónicos. Los grupos de simetría enumerados son los grupos completos con los subgrupos de rotación dada entre paréntesis (igualmente para el número de simetrías). Construcción calidoscopio de Wythoff es un método para construir poliedros directamente desde sus grupos de simetría. Tenemos una lista de símbolo de referencia de Wythoff para cada uno de los sólidos platónicos.

Poliedro	Símbolo de Schläfli	Símbolo Wythoff	Poliedro dual	Simetrías	Grupo de simetría
tetraedro	{3, 3}	3 \| 2 3	tetraedro	24 (12)	T _d (T)
cubo	{4,} 3	3 \| 2 4	octaedro	48 (24)	O _h (O)
octaedro	{3, 4}	4 \| 2 3	cubo	48 (24)	O _h (O)
dodecaedro	{5, 3}	3 \| 2 5	icosaedro	120 (60)	I _h (I)
icosaedro	{3, 5}	5 \| 2 3	dodecaedro	120 (60)	I _h (I)

En la naturaleza y la tecnología

El tetraedro, cubo, octaedro y todo ocurre de forma natural en estructuras cristalinas. Estos no agotan el número de posibles formas de cristales. Sin embargo, ni el icosaedro regular ni el dodecaedro regular se encuentran entre ellos. Una de las formas, la llamada piritoedro (llamado así por el grupo de los minerales de la que es típico) tiene doce caras pentagonales, dispuestas en el mismo patrón que las caras del dodecaedro regular. Las caras de la piritoedro son, sin embargo, no regular, así también el piritoedro no es regular.

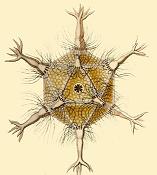
Icosahedra Circogonia, una especie de Radiolaria, la forma de un icosaedro regular.

En el siglo 20, Ernst Haeckel describió (Haeckel, 1904) una serie de especies de Radiolaria, algunos de cuyos esqueletos tienen forma de varios poliedros regulares. Los ejemplos incluyen octahedrus Circoporus, Circogonia icosahedra, Lithocubus geometricus y Circorrhegma dodecaedros. Las formas de estas criaturas deberían ser obvios a partir de sus nombres.

Muchos virus , como el virus del herpes, tiene la forma de un icosaedro regular. Estructuras virales están construidas con idénticos repetidos proteína subunidades y el icosaedro es la forma más fácil de montar utilizando estas subunidades. Un poliedro regular se utiliza porque puede ser construido a partir de una única proteína unidad básica que se utiliza una y otra vez; Esto ahorra espacio en el viral genoma.

En meteorología y climatología, modelos numéricos globales de flujo atmosférico son de creciente interés que emplean las redes que se basan en un icosaedro (refinados por triangulación) en lugar de la de uso más común / longitud latitud cuadrícula. Esto tiene la ventaja de la resolución espacial distribuido uniformemente sin singularidades (es decir, el polos) a expensas de algo mayor dificultad numérica.

Geometría de estructuras espaciales a menudo se basa en los sólidos platónicos. En el sistema MERO, sólidos platónicos se utilizan para la convención de nombres de diferentes configuraciones del marco espacio. Por ejemplo T + ½O refiere a una configuración hecha de un medio de octaedro y un tetraedro.

Sólidos platónicos se utilizan a menudo para hacer los dados , porque dados de estas formas se pueden hacer justo. Dado de 6 lados son muy comunes, pero los otros números se utilizan comúnmente en juegos de rol. Tales dados se refieren comúnmente como d n donde n es el número de caras (d8, d20, etc.); ver Dados de rol para más detalles.

Dados poliédricos se utilizan a menudo en juegos de rol.

Estas formas con frecuencia aparecen en otros juegos o puzzles. Puzzles similares a un cubo de Rubik llegado en las cinco formas - ver poliedros magia.

Poliedros relacionados y politopos

Poliedros uniformes

Existen cuatro poliedros regulares que no son convexos, llamado Poliedros de Kepler-Poinsot. Todos ellos tienen simetría icosaédrica y pueden obtenerse como se constelaciones del dodecaedro y el icosaedro.

cuboctaedro

icosidodecaedro

La próxima poliedros convexos más regular después de los sólidos platónicos son el cuboctaedro, que es una rectificación del cubo y el octaedro y el icosidodecaedro, que es una rectificación del dodecaedro y el icosaedro (la rectificación del tetraedro auto-dual es un octaedro regular). Estos son tanto sentido cuasi-regular que son vertex- y el borde uniforme y tienen caras regulares, pero las caras no son todos congruentes (que viene en dos clases diferentes). Ellos forman dos de los trece Sólidos de Arquímedes, que son el convexa poliedros uniformes con simetría poliédrica.

El poliedros uniformes formar una clase mucho más amplia de los poliedros. Estas cifras son vértice uniforme y tienen uno o más tipos de regular o polígonos estrellas para los rostros. Estos incluyen todos los poliedros mencionado anteriormente junto con un conjunto infinito de prismas, un conjunto infinito de antiprismas, y otras 53 formas no convexas.

La Sólidos de Johnson son poliedros convexos que tienen caras regulares, pero no son uniformes.

Tessellations

El árbol teselaciones regulares del plano están estrechamente relacionados con los sólidos platónicos. De hecho, uno puede ver los sólidos platónicos como los cinco teselaciones regulares de la esfera . Esto se hace mediante la proyección de cada sólido sobre una esfera concéntrica. Los rostros se proyectan hacia regulares polígonos esféricos que cubren exactamente la esfera. Se puede demostrar que cada teselación regular de la esfera se caracteriza por un par de enteros {p, q} con 1 / p + 1 / q> 1/2. Del mismo modo, una teselación regular del plano se caracteriza la condición 1 / p + 1 / q = 1.2. Hay tres posibilidades:

{4, 4} que una suelo de baldosas cuadradas,
{3, 6} que es una mosaico triangular, y
{6, 3} que es una baldosas hexagonales (doble al mosaico triangular).

De una manera similar se puede considerar teselados regulares de la plano hiperbólico. Estos se caracterizan la condición 1 / p + 1 / q <1/2. Hay un número infinito de dichos mosaicos.

Dimensiones superiores

En más de tres dimensiones, poliedros generalizar a politopos convexos, con más dimensiones politopos regulares que son los equivalentes de los sólidos platónicos tridimensionales.

En la mitad del siglo 19 el matemático suizo Ludwig Schläfli descubrió los análogos de cuatro dimensiones de los sólidos platónicos, llamado regular convexo 4-politopos. Hay exactamente seis de estas cifras; cinco son análogos a los sólidos platónicos, mientras que el sexto uno, el De 24 celdas, no tiene analogía menor dimensión.

En todas las dimensiones superiores a cuatro, sólo hay tres politopos regulares convexos: el simplex, el hipercubo, y la cruz-politopo. En tres dimensiones, éstos coinciden con el tetraedro, el cubo y el octaedro.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Platonic_solid&oldid=198915089 "

See also ebooksgratis.com: no banners, no cookies, totally FREE.